顾及变量相关性的主成分分析法在森林蓄积量估测中的应用1)

崔博文 佘济云 张廷琛 刘兆华 王潇

(中南林业科技大学，长沙，410004)

森林是地球上最重要的资源之一，是生物多样性的基础，人类生存发展的保障[1]。森林蓄积量是评判森林质量的重要指标，森林蓄积量指一定森林面积存在的林木树干部分的总材积，能够直接反映森林资源的丰富程度，所以，精准且迅速地对森林蓄积量进行预测具有非常重要的意义。

传统的森林蓄积量统计虽然准确率较高，但是需要耗费大量的人力及物资，目前随着计算机技术、遥感(RS)、地理信息系统等技术的逐渐成熟，通过将数学模型、遥感影像及部分实地数据联合，从而对森林蓄积量进行反演的研究方法逐渐成为研究的热点之一。

在进行森林蓄积量估测时，遥感变量的筛选尤为重要，过多的数据不仅会存在共线性问题，而且会增大计算量;选择数据较少会造成数据没有代表性，结果不准确的问题。目前在遥感因子筛选较为常用的方法主要是Pearson相关系数法及主成分分析法。刘明艳等[2]以老秃顶子自然保护区为研究区，采用Landsat8 OLI数据以及实地数据作为数据源，通过使用主成分分析法提取变量，构建了线性回归估测模型，模型预估精度达到了92.18%；郝泷等[3]以Landsat8 OLI为遥感数据源，森林资源二调数据为地面数据源，通过使用主成分分析法对数据降维并构建多元线性回归模型，最终精度达到80.24%；周如意[4]以浙江省龙泉市作为研究区，通过使用Pearson双变量相关性分析方法对自变量进行相关性分析，构建模型后估测精度达到74.96%。

由于Pearson相关系数法只能反映变量间线性关系的强弱[5]，主成分分析法虽可以避免发生共线性问题，但容易造成数据冗余[6]，本研究在原有2种筛选变量方法的基础上增加了一种先采由Pearson相关系数法去除相关性较小的变量，再对剩余变量进行主成分分析的筛选方法(PCA-P)。通过将3种筛选方法所获得的自变量分别构建多元线性回归模型(MLR)、K最近邻模型(KNN)、随机森林模型(RF)、支持向量机模型(SVR)4种蓄积量反演模型，研究不同变量选择方法及不同模型对蓄积量估测精度的影响，以期得到精度最高、拟合度最好的蓄积量反演估测模型。

1 研究区概况

选取湖南省怀化市靖州县排牙山国家森林公园作为研究区，排牙山国家森林公园的地理坐标为109°27′8″～109°37′57″E,26°26′1″～26°35′20″N(图1)。总面积3 745.41 hm2,以低山地貌为主，地势中间高，两边低，呈带状延伸。森林公园属亚热带季风湿润气候区,气候温和,雨量充沛,年均气温17.0 ℃,年均降水量为1 250 mm,无霜期为290 d左右。主要成土母岩为紫砂岩，土壤以紫色砂岩发育而成的紫色土为主。林分类型以杉木人工林为主，林场分类为以保护为主的生态公益型林场[7]。

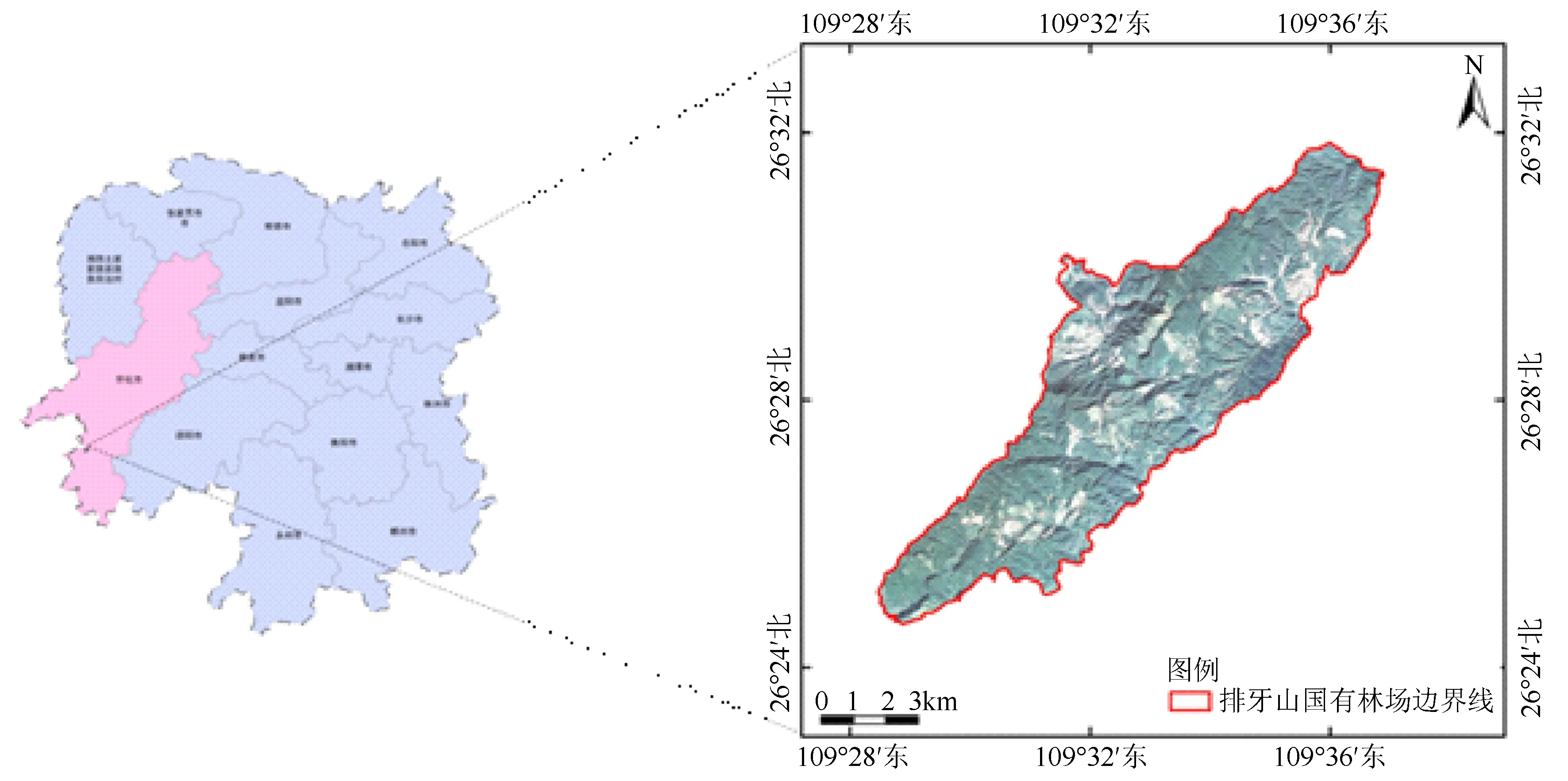
图1 研究区位置

2 研究方法

2.1 数据来源及处理

2.1.1 地面数据来源及预处理

样地地面数据使用靖州县森林资源二类调查数据为基础。由于地面数据数量较大，树种较为复杂，本研究所选用的蓄积量估测模型不足以支撑多树种蓄积量共同反演，因此仅保留杉木样本作为本次试验的研究对象。使用标准差分析方法，剔除离散程度较大的样地点，剩余110个样地点作为试验样地点(图2)。样地蓄积量范围为70.59～507.12 m3·hm-2，标准差为91.34 m3·hm-2,变异系数为0.35。

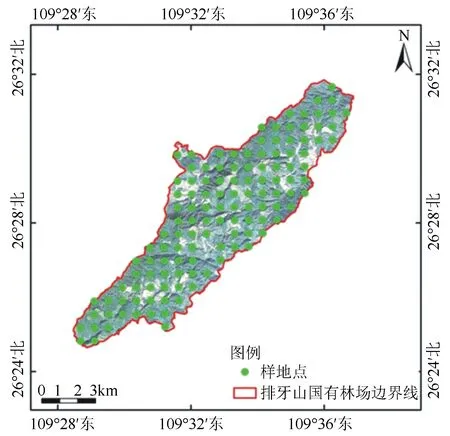
图2 样地点分布图

2.1.2 遥感数据来源及处理

影像选用与森林资源二类调查同时期的Landsat8 OLI影像，通过地理空间数据云免费下载。对遥感数据进行辐射定标、大气校正、正射校正、几何校正、地形校正，再将数据矢量化，使单块样地的像元亮度值与蓄积量一一对应。

2.2 遥感变量提取与筛选

2.2.1 遥感变量的提取

试验共提取遥感因子83个，包括6个Landsat8OLI单波段因子(由于B1波段用于观测海岸线、B9为卷云波段所以不计入)、3×3窗口下的8个纹理特征值、通过单波段因子计算得到的69个植被指数。植被指数计算公式见表1，其中B2为蓝波段、B3为绿波段、B4为红波段、B5为近红外波段、B6为短波红外1、B7为短波红外2；L为随植被密度变化的参数，L为0.5时消除土壤反射率的效果较好[6]。

表1 植被指数

2.2.2 特征选择方法

目前，Pearson相关系数法及主成分分析法在筛选变量时应用较为广泛[8]。应用Pearson相关系数法分别对每个指标进行分析，其结果往往是孤立的，并不是综合的，而盲目减少指标会损失很多可能有用的信息，容易出现错误的结论[8]。使用主成分分析法能有效地提取初始数据的信息，得到的特征根数量远小于原始变量，每个特征根之间相互独立，不会出现共线性问题,但如果将全部原始数据直接进行主成分分析，容易造成数据冗余，造成结果不准确[9]。为提高准确性，本研究在原有的2种筛选变量方法基础上，增加了Pearson相关系数法联合主成分分析法(PCA-P)筛选变量，即先使用Pearson双变量相关系数法对原始数据进行筛选，保留相关性大于0.5的变量，再使用主成分分析法对其进行降维。使用这种方法可以综合考虑所有变量，去除数据冗余的同时，保留数据的目标信息，提高估测精度。

2.3 蓄积量估测模型的构建

使用3种筛选方法提取的特征构建多元线性回归、支持向量机、随机森林法、K最近邻4种回归模型。多元线性回归通常用来研究1个因变量和多个自变量的变化关系，主要是以多个主要影响因素作为自变量来解释因变量的变化，当多个自变量与因变量之间是线性关系时，所进行的回归分析就是多元线性回归[10]。随机森林算法属于集成学习法中的套袋法，随机森林模型采用自助法(Bootstarp)有放回地抽样从原始数据中随机选择n个样本构建CART决策树，从所有原始变量中随机抽取若干个特征变量用于决策树构建，最终组成随机森林模型。随机森林算法的优点在于其结果不容易发生拟合且具有很好的抗噪声能力，而构建模型的关键在于其决策树的数量选择[11-12]。支持向量机的基本原理是通过某种事先选择的非线性映射将输入向量x映射到1个高维特征空间，在这个空间中构造最优分类超平面，从而使正例和反例样本之间的分离界限达到最大，优化模型的方法是使用结构风险最小化原则，其核函数的选择将直接影响其估测结果[13-15]。K最近邻属于数据挖掘分类中的一种，其基本原理是使用一致类别的样本作为参考，计算所有已知样本与未知样本的距离，最终选取出K个与未知距离最近的已知样本，采用少数服从多数的投票法则来进行分类，其关键在于K值的选择。在应用中可采用交叉验证法来选择最优的K值[16-18]。

本次试验设置随机森林法模型决策树数目为100，K最近邻模型K值从2循环到50，当K=13时，模型精度最好。因此选择13作为本次试验K值。

2.4 模型评价

本试验采用检验模型的方法为留一交叉法，分别计算各模型的决定系数(R2)，均方根误差(RMSE)，以及相对均方根误差(RRMSE)3个指标对模型进行精度评价，指标计算公式如下：

(1)

(2)

(3)

式中：yi为估测样地蓄积量；y为实测样地蓄积量；N为样地数目。

3 结果与分析

3.1 特征选择结果

3.1.1 Pearson相关系数法特征选择结果

将83个遥感变量进行Pearson双变量相关性检验，在0.01显著水平上，相关性大于0.5的遥感变量共17个[19-20]。为保证参与建模变量的准确性，引入方差膨胀因子(VIF)对遥感变量进行共线性分析，去除方差膨胀因子大于10的变量，得到的遥感变量为IB2(相关性0.716)、IMSR(相关性0.623)、IND25(相关性0.597)。

3.1.2 主成分分析法特征选择结果

对83个原始变量进行主成分分析，分析结果如表2所示，得到3个主成分，累计贡献率为93.42%，选择这3个特征根作为主成分分析法反演蓄积量模型的自变量。

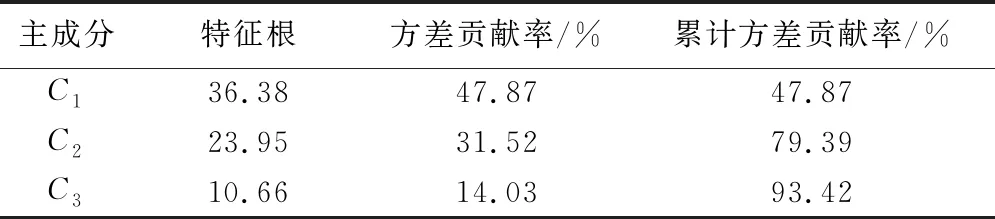
表2 主成分分析

3.1.3 PCA-P特征选择结果

计算83个原始变量与蓄积量的Pearson相关系数，保留在0.1显著水平上相关系数大于0.5的变量(表3)，并对其进行主成分分析，分析结果如表4所示。共得到2个特征根，累计贡献率达到88.992%，选择这2个主成分作为PCA-P反演蓄积量模型的自变量。

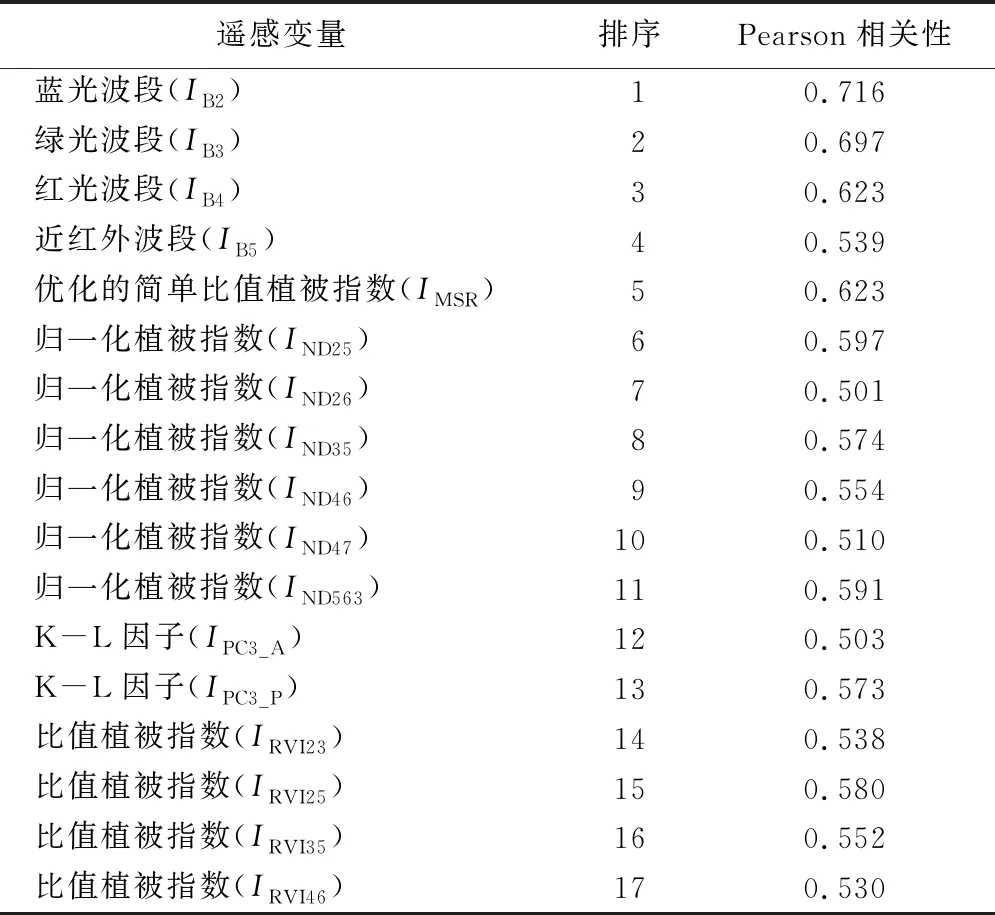
表3 遥感变量与蓄积量的相关性

表4 PCA-P分析

3.2 构建模型结果

3.2.1Pearson相关系数筛选变量蓄积量估测模型构建

将通过Pearson相关系数法及方差膨胀因子得到的3个遥感变量构建蓄积量估测模型，参与构建的模型分别为多元线性回归模型、K最近邻模型、随机森林模型、支持向量机模型。分别计算统计各模型的决定系数、均方根误差、相对均方根误差。

由表5可知，通过Pearson相关系数筛选得到的变量，在K最近邻模型中取得了最好的效果，决定系数为0.50，均方根误差为49.1 m3·hm-2，模型精度达到76.7%；线性回归模型仅次于K最近邻模型，其模型决定系数为0.48，精度达到75.9%；随机森林模型效果最差，拟合度仅为0.37。K最近邻模型蓄积量散点图见图3。

表5 Pearson筛选变量构建模型结果

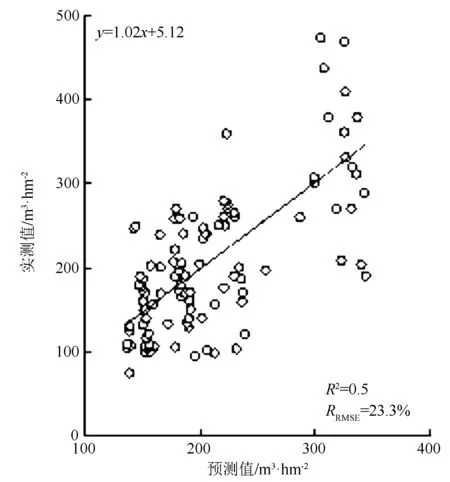
图3 K最近邻模型蓄积量散点图

3.2.2 主成分分析法筛选变量蓄积量估测模型构建

将通过主成分分析法得到的4个特征根参与构建多元线性回归模型、随机森林模型、支持向量机模型、K最近邻模型，分别计算统计各模型的决定系数、均方根误差、相对均方根误差。

由表6可知，在全部变量参与主成分分析并构建模型的情况下，多元线性回归模型效果最好(R2=0.47)，其他3种机器学习法决定系数较低，且支持向量机模型决定系数为负值，说明冗余数据中存在内生变量的滞后值。多元线性回归模型蓄积量散点图见图4。

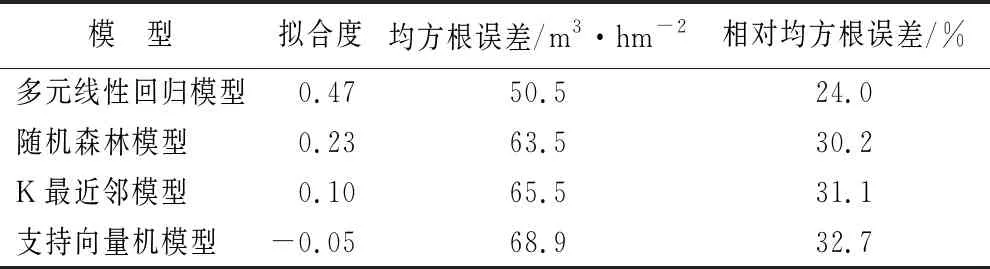
表6 主成分分析法筛选变量构建模型结果

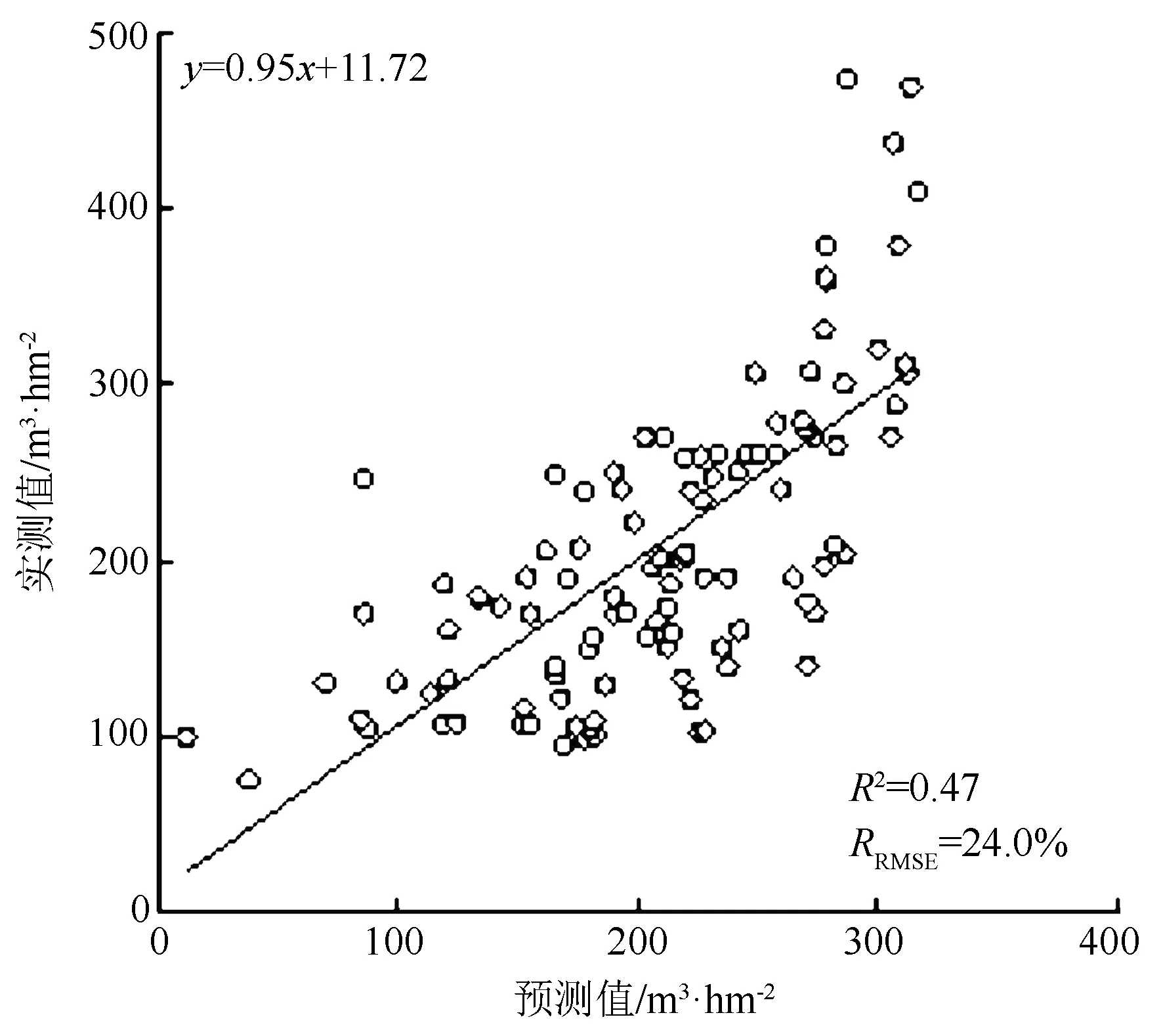
图4 多元线性回归模型蓄积量散点图

3.2.3 PCA-P蓄积量估测模型构建

将通过PCA-P得到的两个特征根参与构建多元线性回归模型、随机森林模型、支持向量机模型、K最近邻模型，分别计算统计各模型的决定系数、均方根误差、相对均方根误差

由表7可知，通过PCA-P作为筛选方法所构建的模型精度且3种机器学习法结果优于多元线性回归模型，其中随机森林法效果最好，决定系数达到0.59，其均方根误差为46.5 m3·hm-2，相对均方根误差为22.1%；K最近邻模型决定系数为0.52，精度为75.3%；支持向量机决定系数为0.46，精度为75.3%；多元线性回归模型决定系数为0.40，其均方根误差为24.3%。随机森林法模型蓄积量散点图见图5。

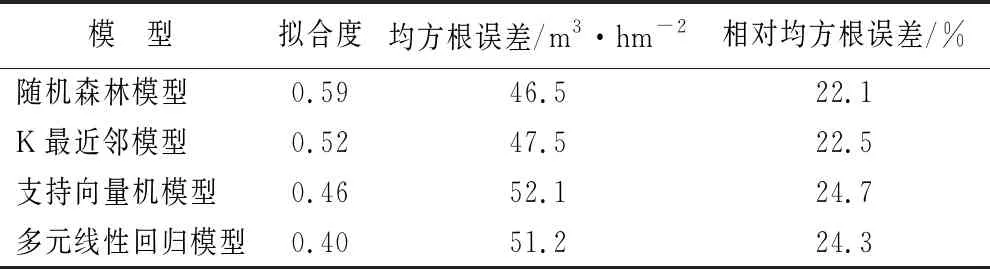
表7 PCA-P筛选变量构建模型

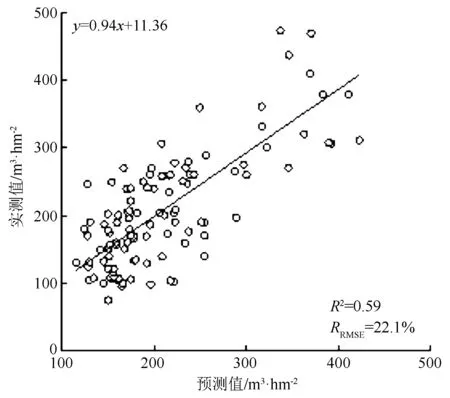
图5 随机森林法模型蓄积量散点图

3.3 研究区蓄积量反演结果

分别构建3种筛选方法中最优模型的蓄积量反演图，即使用Pearson相关系数法构建的K最近邻模型、使用主成分分析法构建的多元线性回归模型组合、使用PCA-P构建的随机森林模型。由图6可知，3种筛选方法构建的蓄积量反演结果均体现出蓄积量主要分布在研究区东北部及中部，西南部分布较少。

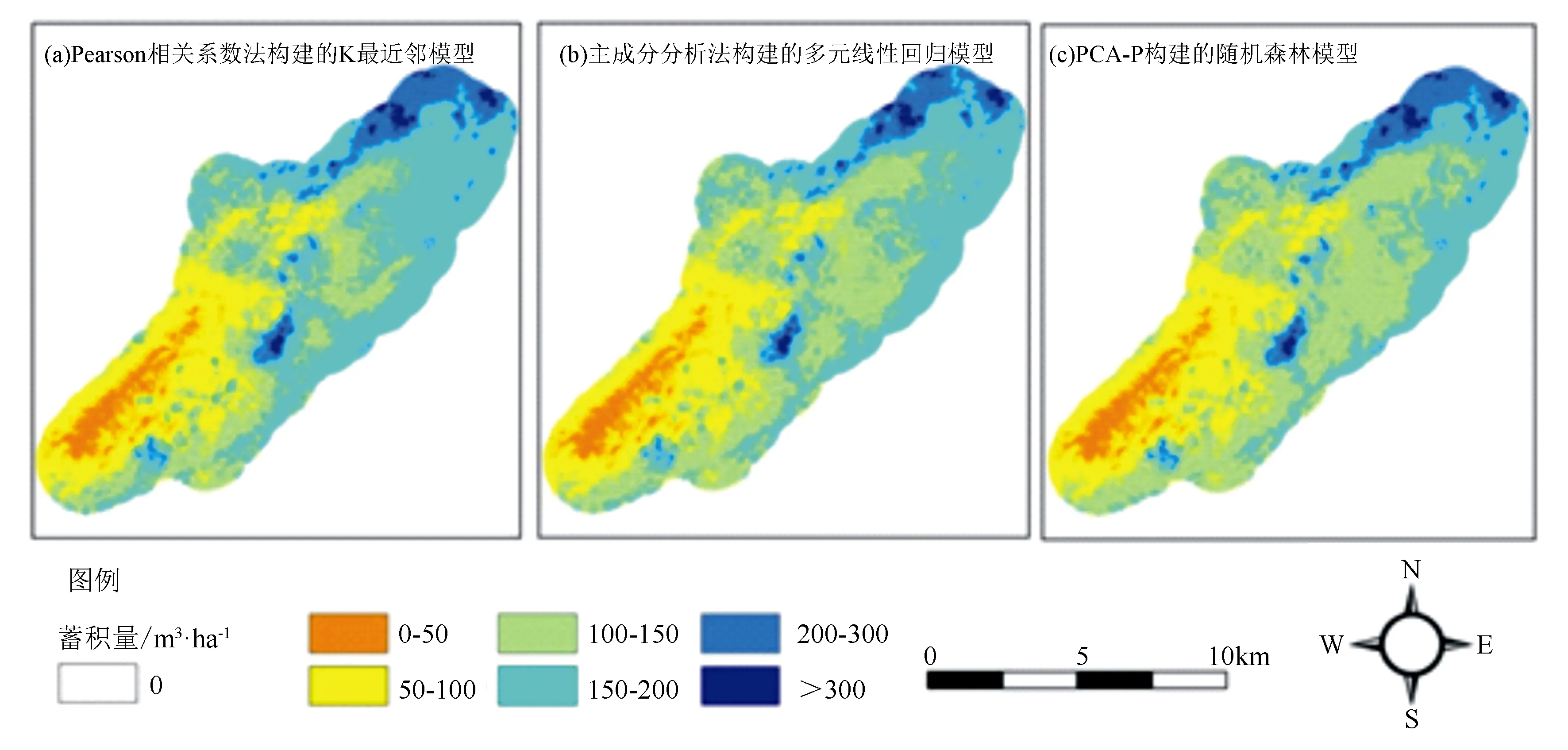
图6 排牙山林场蓄积量分布

4 结论与讨论

本研究选取靖州县排牙山国有林场作为研究区，使用Landsat8 OLI数据作为遥感数据源，结合森林资源二类调查数据，通过将Pearson相关系数法及主成分分析法结合得到一种新的筛选方法(PCA-P)并构建4种不同模型，为进行对比分析构建了Pearson相关系数法及主成分分析法的估测模型，并使用留一交叉验证的方法对结果进行精度检验。

使用Landsat8 OLI数据提取的光谱变量与森林蓄积量具有较强相关性，所以使用Landsat8 OLI数据对森林蓄积量进行反演是可行的。将2种筛选方式结合可以有效去除数据冗余并保留目标信息，提高蓄积量估测精度。使用PCA-P结合随机森林法模型达到了最高精度，其决定系数为0.59，均方根误差为46.5 m3·hm-2，相对均方根误差为22.1%。

本研究中发现，将Pearson相关系数法与主成分分析法联合起来筛选特征能够在降低维度的同时不丢失原有数据的大部分信息，且通过对比发现，使用不同筛选方法构建同一种反演模型时，模型拟合度及精度均有较大提高，如支持向量机模型在使用Pearson相关系数法、主成分分析法时，决定系数分别为0.42、-0.05，相对均方根误差分别为25.9%、32.7%，但使用PCA-P作为筛选方式构建支持向量机模型，决定系数达到0.46，相对均方根误差达到24.7%。PCA-P为利用卫星影像对森林蓄积量反演在筛选特征值这一关键步骤提供了一种新的思路。使用PCA-P作为筛选方法构建的随机森林模型是否在北方林地也可以发挥较好效果，需要进一步验证。由蓄积量反演图可知，每公顷林分蓄积量大于300 m3时，反演模型出现饱和现象，如何解决光谱饱和问题需进一步验证。由于研究区树种主要为针叶林，所以本研究对针叶林蓄积量研究具有一定参考价值。