平行四边形面积公式固着化的原因分析与策略研究

蒋鑫源

【摘   要】平行四边形是学生在学习了长方形、正方形之后所接触到的第三个几何图形，它也是后续学习三角形、梯形等图形的基础。通过调查发现，学生存在面积公式的固着现象，即认为凡与此相关的问题都应该借助面积公式来解决。该现象背后的原因与格式塔心理学中“心理场”概念以及知觉组织原则相关。公式的固着现象可以通过调动学生的几何直觉、打破公式的推导固化、加强课后练习质量等策略来解决。

【关键词】公式固着;心理场;知觉组织;推导;几何直觉;课后练习

一、一道题目暴露的问题

培养学生“数学的眼光”是当前数学课程蕴含的核心素养之一。数学的眼光是与数学学科相关的一种独特的思考角度。[1]“独特”一词体现出眼光的个性化，人通过不同的角度可能会获取不同的信息、经历不同的思维过程，自然出现不同的生成。在教学实践中发现，学生往往对平行四边形记忆最深刻的就是面积公式，这种过分的熟悉不利于学生“数学眼光”的培养。国外学者Laura Macchi 与Maria Bagassi等人在研究中发现：对于顿悟问题的解决，默认反应并不能得到结果，反而有可能导致“固着（Fixation）”。他们引用韦特海默“正方形与平行四边形”一题（如图1）来加以解释。[2]也就是说，对于平行四边形面积的相关问题，学生的默认反应就是找到底与高后，将数据代入面积公式计算即可。若无法获得公式信息，学生就很难利用其他方式来解决。

为研究公式的认知固着现象，笔者在学生学习了平行四边形的面积之后进行“正方形与平行四边形”一题的测试，测试对象为北京市S小学五年级某班的学生，共计36人。测试结果显示，有59%的学生采用公式法求解平行四边形的面积。有12%的学生在采用公式法的同时尝试使用转化法，但转化法仍然未脱离面积公式。学生依据底和高的关系，将平行四边形转化为一个大小相等的长方形来解决（如图2）。除此之外，有18%的学生无法解决本题。另有11%的学生尝试通过底边与邻边相乘来解决问题，但无法获得较长边的长度，因此没能得出准确结果。从测试结果可以看出，有71%的学生能够解决该问题，且都使用了面积公式;29%的学生既无法利用公式解决问题，也没有其他思路。测试结果表明，学生存在平行四边形面积公式固着的现象。

二、公式固着现象产生的原因分析

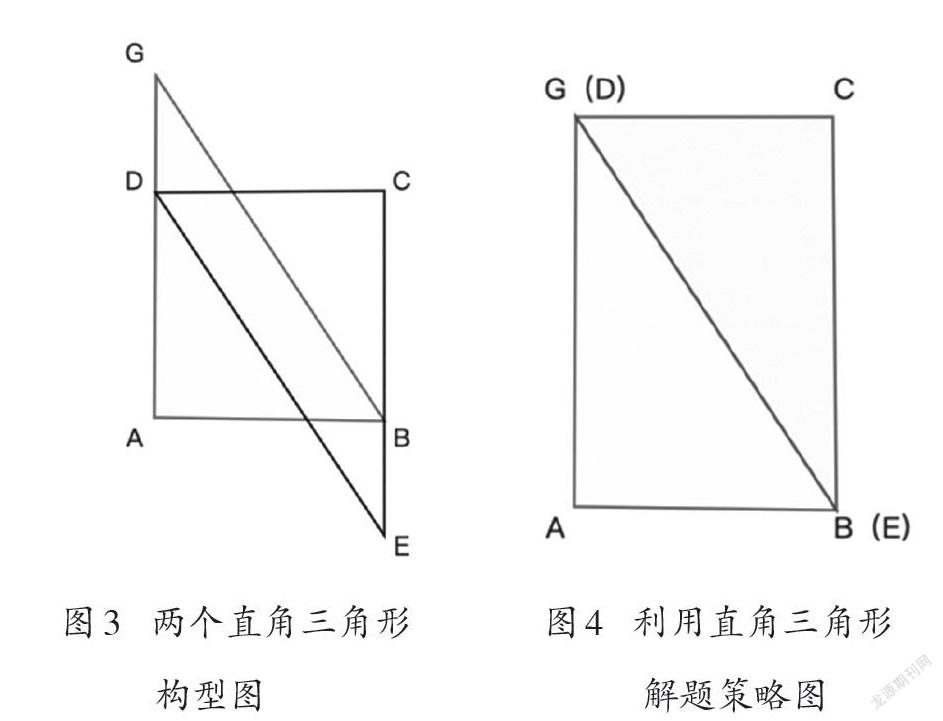
韦特海默对本题的设计是与人的心理活动相关的。格式塔心理学遵从整体论，认为主体的心理现象具有特定的整体属性，对部分的感知是依赖于整体属性的，整体不能分解为简单的元素。该理论强调知觉的作用，认为知觉到的事物大于眼睛看到的事物，并且每个人都是依照组织律进行知觉组织的。对本题来说，学生受到正方形、平行四边形等熟悉图形的影响，遵从熟悉性原则进行知觉组织，以致眼睛看到的就是一个正方形和一个平行四边形。实际上，本题中除了正方形和平行四边形以外，还存在两个直角三角形（如图3）。学生之所以无法看到这两个直角三角形，也是因为知觉组织。由于两个直角三角形的构型造成图形与背景之间的区分度较小，从而使其难以成为知觉对象。此外，在格式塔理论中有两个重要的术语，即冲突（conflict）和掩蔽（masking）。[3]学生看不到两个直角三角形的存在，正是由于熟悉性法则战胜了图形与背景法则，从而将两个直角三角形掩蔽。因此，如果学生能够将图形与背景进行转换，使两个直角三角形得以呈现，那么即便是没有学习过平行四边形面积公式，学生也可以将两个三角形重新组织成一个长方形（如图4），进而获得正方形与平行四边形的面积之和，最后利用“部分—整体”关系得到平行四边形的面积。

学生无法摆脱公式的束缚，主要是受到场的影响。格式塔心理学提出心理场（psychological field）与物理场（physical field）两个概念。前者指观察者心目中的世界，后者指物理学家研究的世界。个体的行为与心理场有关，如果个体的场与目标之间是同质的，那么个体与场之间将处于平衡状态;如果个体的场与目标之间是异质的，那么个体将处于不平衡状态且具备动力特征。当个体处于不平衡状态时，会对知觉场进行重新组织，从而实现稳定与平衡。良好的心理场形成时，问题就迎刃而解了。[4]因此，如果学生总是能够使用面积公式解决问题，那么个体与目标之间是同质的，个体与场之间形成稳定的、平衡的状态。但当学生发现面积公式不能支持问题解决时，则个体与目标之间是异质的，个体将处于不平衡状态，需要对知觉信息进行重新组织以达到新的平衡，从而解决问题。

三、破除公式固着的相关策略

（一）借助几何直觉，点燃学生思维

在康德的数学哲学中直觉拥有重要地位，康德认为人类所有经历都符合概念和直觉条件，直觉是由时间与空间强加的，概念是由理解范畴强加的，因此直觉对于几何量（magnitude）的认知是不可或缺的。[5]教师在进行平行四边形面积的教学时，不应该将内容拆分为“数方格”“转化图形”“推导公式”等几个板块后放入袋子内等待学生索取，而应该让学生能够依赖几何直觉，发现平行四边形和已有经验中的长方形之间具有内在联系，从而对平行四边形作出重新的组合、改編和匹配。也就是说，将平行四边形转化为长方形的过程应该是学生根据结构自主进行的转化，而非由教师引领的，因为学生具备消除困扰、将已有结构转化为更好的结构的本能。实际上，良好均衡的知觉场的形成需要问题解决者超越对于事物表面特征的认识，而领悟到事物之间的内在联系。[6]韦特海默在《创造性思维（Productive Thinking）》一书中提到，平行四边形面积的教学不在于公式，而在于真正的理解和解决问题的能力。学生对该问题的真正理性解决与外部程序解决之间是有很大区别的。[7]

（二）打破推导固着，建立动态眼光

面积是几何图形的属性之一，而图形在数学的发展历史中占据重要地位。早在公元前6世纪到公元前4世纪，希腊人就对几何量给予充分的关注。图形对他们而言既是符号，也是推理的工具。[8]古希腊哲学家亚里士多德将量分为连续量与离散量，包含线、面、体、时间、空间、数字、语言这七种量。其中，数字和语言属于离散量，而线、面、体、时间、空间则属于连续量。[9]19～20 世纪，英国哲学家、数学家罗素（Bertrand Arthur William Russell，1872—1970）在他的著作《论数与量的关系》中谈及强度量与广延量，认为广延量是可以表述为“整体=部分+部分”的， 而强度量的整体与部分之间是一致的。因此，从量的角度来看，面积既是连续量，也是广延量，而几何图形既是抽象符号，又是推理工具。

在教学实践中，教师通常利用“数方格”和“转化法”来完成面积公式的推导过程。事实上，这类方法利用了面积作为广延量的属性，即通过考虑部分与整体的关系实现面积公式的推导。如果将教学实践看作是一架天平，天平的左侧是面积的广延量属性，右侧是面积的连续量属性，那么显然这架天平已经失去了平衡。认识面积的连续量属性，并从运动变化的角度对它进行构建，可以培养学生动态的数学思维。

以学生学习平面图形面积的整体过程来看，往往是将陌生的图形转化为熟悉的图形，然后推导出新图形的面积公式。并且严格遵循教科书顺序，即“长方形→平行四边形→三角形→梯形”。然而，学习的道路绝不止一条，如果教师选择使用固化的方式进行课堂教学，那么学生则不可避免地形成固化的思维。

除了静态的转化、推理活动以外，运动变化的方式同样适用于几何图形的学习。比如梯形可以和长方形、正方形、三角形、平行四边形等图形实现公式通用。通过变化梯形的上下底，直到二者相等，可以将梯形转化为平行四边形或长方形，梯形面积公式中上下底的和也就是平行四边形或长方形两条底边的和;当梯形的上底为0时，则转化为一个三角形，此时上下底之和转变为三角形的底边（如图5）。由于梯形的上下底之和与高保持不变，无论以上哪种图形，面积大小都不会发生变化。因此，平行四边形的面积公式并不是一成不变的，而是可以根据思考方式不同而产生不同的抽象结果。

平行四边形面积的学习方法除了“数方格”“转化图形”“变化梯形的上下底长度”以外，还可以从“线动成面”的角度展开学习。如图6所示，长方形的面积可以看作是线段EF由AB位置沿垂直方向平移至CD位置所形成的轨迹，其大小由线段EF的长度以及线段AB到线段CD之间的距离决定。同理，平行四边形的面积则可以看作是线段EF由AB位置沿某一角度平移至CD位置所形成的轨迹，其大小同样由线段EF的长度以及线段AB到线段CD之间的距离决定。[10]三角形与梯形的特殊之处是横向线段EF在运动过程中不断缩小，因此面积大小由横向线段EF运动变化的平均值与运动距离所决定（如图7）。

平行四边形面积公式的推导是一个开放性的问题，教学时需要打破固化的推导方式，通过设计联系的、运动的学习活动来扭转学生唯公式化的问题解决方式。

（三）借助课后练习，锻炼学生眼光

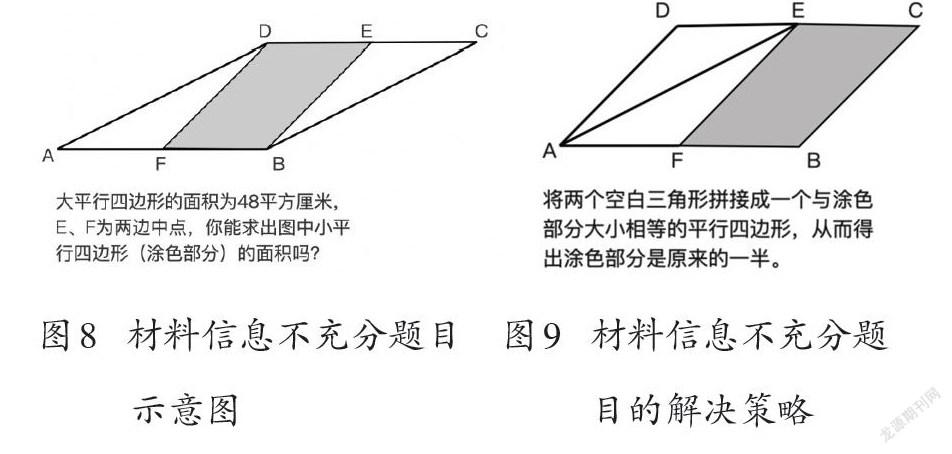
课后练习的作用在于既能巩固所学知识，又能锻炼学生的眼光。在当前双减背景下，如何在压减课后作业总量的同时，又能保证创造性思维的培养？这就要求教师强化作业的质而减少作业的量。相比以往铺天盖地的公式运用性题目，教师更应该选取能够锻炼数学眼光与数学思维的练习题。要创造条件培养学生大胆设想的习惯，创设一些条件不够充分、具有创造性空间的问题来培养学生的猜测能力。比如下面这题（如图8），学生可以从图形的结构出发，根据题目的要求将图形进行重组，从而构造出新的图形结构来解决问题（如图9）。也可以从面积公式的角度考虑，以达成问题的解决。因此，相比单纯的公式运用性练习，教师可以布置开放性强、材料信息不充分、从多个角度进行思考的练习，进一步锻炼学生的数学眼光。

四、原因及策略总结

从上述内容可知，学生在学习平行四边形面积公式的过程中存在的误区包括推导误区与应用误区。推导误区体现在课堂教学中公式的推导方式固化，即只考虑面积的广延量属性，采用“数方格”“转化图形”等方式推导面积公式，而忽视面积的连续量属性，不能以动态的眼光与方式看待该内容。公式的应用误区体现在问题解决过程中凡与之相关的内容都要借用公式解决，而无法对知觉信息进行重新组织与转换，以找到新的解决问题的策略。

造成以上误区的原因一方面与教师对知识内容的理解有关，另一方面与人的心理场和知觉组织原则相关。因此，教师要加强对知识属性本身的理解，借助几何直觉的力量，寻找事物之间的内在联系，从而打破传统的教学方式，不断创新，实施培养学生核心素养的课堂教学。此外，思维和推理都依赖于知觉的过程，人的感知过程就是从对整体广泛的、模糊的认识到对具体细节的把握，以致呈现出有组织的、清晰的想法。[11]教师可以通过创造与心理场不相符合的行为目标而促进学生产生不平衡状态，从而打破思维定式，寻找新的解决问题的策略。

参考文献：

[1]胡晋宾，刘洪璐.数学眼光的内涵及培养[J].中学数学月刊，2021（2）：17-20.

[2]MACCHI L，BAGASSI M. Intuitive and analytical processes in insight problem solving： a psycho-rhetorical approach to the study of reasoning[J]. Mind & Society， 2012， 11（1）： 53-67.

[3]DESOLNEUX A， MOISAN L， MOREL J M.From gestalt theory to image analysis[M]. New York： Springer Verlag ， 2007： 21-25.

[4]考夫卡.格式塔心理学原理[M].李维，译.北京：北京大学出版社，2010：34-36.

[5]SUTHERLAND D. Kant’s philosophy of mathematics and the Greek mathematical tradition[J]. The Philosophical Review， 2004， 113（2）：157-159.

[6]张敬威，于伟.非逻辑思维与学生创造性思维的培养[J].教育研究，2018（10）：40-48.

[7]WERTHEIMER M.Productive thinking[M].New York： Harper Torchbooks， 1963： 68-69.

[8]GOVANNI F. The rise and development of the theory of series up to the early 1820s[M]. New York： Springer， 2008： 95.

[9]ARISTOTLE. Categories[M]. Translated by COOKE H P， TREDENNICK H. London： Harvard University Press， 1938： 17.

[10]郜舒竹.小学数学这样教：第2版[M].上海：华东师范大学出版社，2021：182-183.

[11]GEORGE W， HARTMANN. Gestalt psychology and mathematical insight[J]. The Mathematics Teacher， 2007（100）： 17-18.

（首都師范大学初等教育学院   100048）