探讨概念图在初中数学单元复习课中的有效运用

查贤钰

(江苏省高邮市送桥镇初级中学 225651)

概念图是一种由来已久的图示展示方法，其依靠节点表示概念，依靠连线表示概念之间的关系，强调整体表述的条理性与清晰性.其能够以最高的效率革除教学环节的无用元素，进而帮助学生掌握概念知识，在初中数学教学活动中对概念图加以应用，从解题、概念记忆、定义辨析等角度开展教学活动，能够更为有效地提升有关课程的授课质量.如何将概念图应用到数学复习课的各个环节，这便是数学教学活动中亟待解决的新问题.

1 依靠概念图布置任务，发起复习指导

单元复习课是以单元内的教学知识为核心的复习指导模式.在初中阶段的数学教学活动中，应用单元复习课能够帮助学生将单元内数学知识按照理论知识的相似性、递进性特点整合起来，进而帮助学生完成数学复习任务.从整体上来看，单元复习课表现出了更强的针对性特点，但对复习流程进行分析，发现复习环节存在的矛盾是不容忽视的：当多个板块的复习知识被整合到同一材料当中，各种理论与概念相互杂糅，学生需要抽调额外的时间来整理复习内容，整体的复习效率随之下降.教师可尝试通过概念图布置复习任务，降低无用信息对于教学活动的干扰，依靠概念图做好复习指导工作.

以苏科版初中数学《代数式》单元的复习活动为例，教师可结合以下例题提出不同的复习任务：

①x+8=24；②5-7；③6y.

任务一：说出例题中属于代数式的算式

任务二：回忆代数式的结构与运算特点

任务三：对代数式进行计算

在学生完成初级运算任务之后，教师可继续给出新的复习任务：在学习代数式知识的过程中，你还学习过哪些关键知识点？请在答案下方罗列出来，例题任务中给出的复习目标比较单一，鼓励学生自主发挥，其能够将一些被忽视的数学灵感带入到课堂当中.在这一环节，学生结合合并同类项、去括号等知识点进行回忆、解题，完成基本运算技巧的整理工作.在对数学概念与定理进行复习的过程中，学生可能已经能够将有关类型的数学问题与其他数学问题分离开来，但由于语言表述能力不佳，其并不能对相关概念进行解读.教师可为学生布置概念辨析题，题目的设计如下：

下列说法正确的是：

①带有未知数的算式一定是代数式.

②代数式中一定带有未知数.

③代数式不包含整式和分式.

围绕问题布置概念辨析任务，帮助学生做好基础层面的奠基工作.结合概念图向学生布置概念分析、知识点整理等任务，能够消除无用信息对于复习活动的影响，进而提升学生的复习效率.

2 利用概念图给出例题，解决难点问题

例题是对相关知识点进行展示的有效材料.在数学复习活动中，教师可尝试通过多元例题帮助学生规划复习方案，提高学生的复习效率.但对于一些知识点比较复杂的例题，其解答难度必然是较高的，在围绕有关问题进行作答的过程中，教师可要求学生通过概念图分析例题，依靠例题解决难点问题.

以苏科版初中数学《二元一次方程》的复习指导为例，教师可结合本单元的重点知识点提出思考问题，围绕“鸡兔同笼”开展计算指导活动：有若干只鸡兔同在一个笼子里，从上面数，有35个头，从下面数，有94只脚.问笼中各有多少只鸡和兔？要求学生对例题进行分析，说明例题中所涉及到的知识点.教师可结合二元一次方程的解法、解题任务提出新的思考问题：二元一次方程如何求解？求解时遵循哪些原则？学生围绕鸡兔同笼问题列出二元一次方程组：x+y=35，4x+2y=94，并通过消元、移项等方式对有关数学问题进行计算.在解答二元一次方程的问题的过程中，学生可能会出现解题上、方法上的失误问题，教师可结合概念图将学生在解题活动中经常出现的错误标记出来，警示学生.

3 利用概念图，梳理综合题解题思路

中学阶段的数学课程设置，每个单元自成一个体系，相关知识的重点考查题型比较类似，解题的思路和方法比较固定.概念图在某种意义上就是多线程的流程图，其表达由起点到终点，梳理了题目由起点到终点的发展和推理过程，概念图的结果即解题思路，可能是一种或者多种，也可以通过几何图形来辅助文本和图示表达.概念图以其在整理思路方面的优势，可以帮助学生理清相关知识点综合题目的解题思路，帮助学生分析问题.学生在教师引导下，进行相关综合题目的概念图逻辑梳理，可以展现解题的思维过程，使解题逻辑可视化，比单一文字说明表达更有成效.在初中数学的单元复习活动中，可以有效帮助学生对已学的单元知识主要题型进行分析和梳理.初中的综合题目类型大都比较经典，有一定的规律可循，考虑到综合题目在中考数学考察中所占的分值比例，可利用概念图帮助学生梳理综合题常用解题思路和方法，加深对主要题型解法的认识，这是非常必要的.

例如苏科版初中八年级上册《一次函数》，其中求解未知函数的解析式是该单元的重点，在该单元知识的考查中，求解一次函数的表达式和解也往往作为综合题目的常用题型，考查学生对这部分知识的掌握.初中阶段该类型题目的解答往往采用直接法和复合法两种方法，在引导学生进行常用解题方法思路的整理时，教师可以要求学生跟随教师的讲解一起绘制概念图.可以先梳理解题思路概念图，再根据具体题目将具体的已知条件代入解题思路概念图进行解题演示.

4 开展个性化的概念图，合理地开展专题训练

概念图是用来组织和表达知识的工具，通常将某一主题相关的概念置于圆圈和方框之中，使用连线将相关概念和命题连接，并在连线上表明两个概念之间的意义关系，用于学生的单元复习事半功倍.在进行单元复习时，教师使用概念图梳理专题内容，可以帮助学生将相关知识点连接起来形成完整的知识体系.尤其是在进行默画概念图时，学生可以通过这种方式发现自己的知识纰漏，暴露出知识盲区，从而进行针对性的训练，提升学生的学习效果.在这个过程中，学生可以结合考虑细碎知识的重要程度以及自己的掌握程度，制作个性化的单元专题概念图，引导其有目的、有组织的复习，掌握学习方法和观察自己的学习情况，树立自我训练意识，从而进行单元专题复习.

例如苏科版八年级上册的《全等三角形》，在该单元专题复习中，需要学生注意对小知识点的掌握以及运用.例如可以从全等三角形的性质、条件等进行梳理，结合具体的全等三角形证明题进行知识的应用.如寻找全等三角形的主题概念图后，连接并补充寻找全等三角形的方法.由于该单元知识往往作为考察题目中的辅助条件进行使用，那么在进行该单元的单元复习梳理时，学生还可以结合经典几何题目进行概念图的梳理，深入分析相关知识点的应用.

5 通过概念图梳理难点，发起师生互动

在全新的复习任务下，概念图具有更强的条理性与指导价值.在初中数学单元复习课上，教师可尝试利用概念图梳理当前数学教学活动中存在的难点问题，引导学生对数学概念进行逐步分析，借由复习活动构建全新的复习指导模式.

以苏科版初中数学《全等三角形》的单元复习活动为例，教师可依靠概念图和例题互相配合，帮助学生复习数学难点，例题的设计如下所示：

如图1，已知有两个三角形的边彼此相接，A、F、E、B处于同一直线上，其中AC⊥CE、BD⊥DF，AE=BF，AC=BD，求证:△ACF≌△BDE.

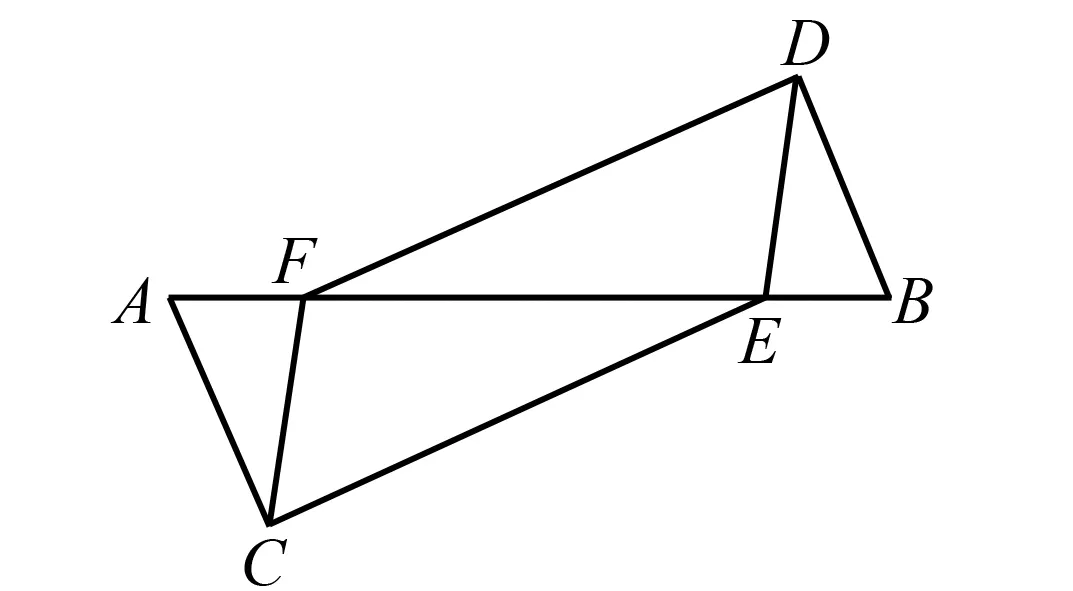
图1

在帮助学生分析数学问题的过程中，教师必须做好知识点、解题思路的梳理工作，教师可为学生绘制相应的概念图，在概念图中提出如下问题：判断两个三角形全等的条件是什么？三个角对应相等的三角形是否也全等？除了问题中所应用的判定方式，你还能够应用哪些方法判断三角形的全等关系？通过问题的解答、关键知识点的梳理，帮助学生完成从解题思路到解题方法的多元化复习.教师还应在概念图中对学生可能出现的错误进行强调，防患于未然.

6 结合概念图优化思路，锻炼数学思维

在初中单元复习课上，概念图不仅能够被应用在概念的辨识、解题方法的记忆等活动当中，其对于学生的数学思维也能够发挥一定的锻炼作用.在围绕概念图开展单元复习指导活动的过程中，教师可尝试利用概念图解决学生的解题思路问题，利用概念图帮助学生规划解题思路，以此来提升学生的数学解题能力.以苏科版初中数学《一元二次方程》的解题教学活动为例，在教学环节中教师可向学生展出不同的数学问题，问题如下：

问题一：x2=16，x2=-3，问x分别等于多少？

问题二：x+8=3，问x等于多少？

这两个问题设计主要是为了帮助学生回忆一元二次方程的特点，在学生对方程进行求解之后，教师可开展一元二次方程的解题思路练习，选择一元二次方程与一元一次方程进行组合对比，如x2+8=40，5x+1=7x，帮助学生借助基础的方程知识回忆方程的解题技巧，将已有的解题灵感带入到后续的解题活动当中，优化学生的解题思路.对于数学教育活动来说，已经学习过的知识未尝不能成为解题灵感，利用概念图将不同的元素整理起来，能够更有效地提高学生的解题水平.

总之，概念图对数学课程中的关键知识点、概念、定义进行了梳理，在学习方法、复习方法等角度指导着学生的复习活动，在应用概念图指导学生进行单元复习的过程中，教师可将教学环节的不同元素、概念带入到课堂当中，依靠例题展示数学复习要求，帮助学生形成更为清晰的复习思路.