初中数学函数应用题的解题对策研究

程 曦

(浙江省杭州市钱塘新区观澜中学 310018)

函数知识是初中数学学习重要的内容之一，在课程中占据着很大的份额，同时也是中考数学中重要的题型，占据着较大比重的分值.因此，作为初中一线数学教师，必须做好初中函数应用题的分析和研究工作，帮助学生认识到函数知识学习的重要性，传授学生解题的对策，培养他们解题的思维，提升他们解题的能力，理解并掌握研究函数的学习方法，从而构建高效课堂，并为学生的中考提供帮助，为后续函数的学习提供方法.

根据笔者多年的教学经验，中考考题年年变，但基本上都是换汤不换药.作为初中数学教师，我们要赢在课堂教学中，提高课堂效率，认真分析函数应用题的知识点，并将其贯彻到中考当中.基于此，笔者认为初中数学教师应从如下几个方面着手.

1 把握知识体系，明确题目要求

在初中数学教学中，教师要想传授学生函数应用题的解题思路和技巧，首先应引导学生把握知识体系，明确题目的要求，提炼题目的有效信息.用通俗的话讲就是让学生读懂题目，这也是提升学生函数应用题解题技巧和能力的前提基础.在浙教版初中数学教材中，函数知识主要分为一次函数、反比例函数和二次函数三种类型，其中，二次函数是中考数学试卷必出的题型，且在总分值中占比较大.为了提高学生二次函数解题的准确率，教师在讲解函数应用题的过程中，就必须先引导学生把握函数知识的整体脉络，提升自身的读题能力，让他们能够快速抓住问题的题干和题眼，明确自己要解决的问题是什么，这样才能帮助学生快速找到解题的思路和方法，准确解决问题.在具体操作中，教师应结合中考的考点和要求，帮助学生理清题目中要考查的知识点是什么，然后能根据解析式找到特殊点，利用描点法画出二次函数的图像，根据图像分析题目中隐含的信息，为解决问题做准备.

例如：如图1所示，抛物线y=ax2+bx+c与x轴相交于点A和点B(2，0)，与y轴相交于点C(0，6)，其对称轴l为x=-2.

图1

(1)求二次函数的解析式和其顶点的坐标.

(2)如果动点N在对称轴l上，动点P在第二象限内的抛物线上，①当PA=NA，PA⊥NA时，求此时点P的坐标；②当四边形PABC的面积最大时，求四边形PABC的面积最大值及此时点P的坐标.

在讲解这道应用题时，教师应巧妙运用转化思想，将复杂的问题向简单化的问题转化，让学生对该问题熟悉起来，这样才能读懂问题，在本题中，可以将点的坐标转化为线段的长度，再把线段的长度转化为方程式，把面积最大值的问题转化为底边(线段)的最大值问题，这样才能简化问题并读懂问题，从而快速、高效、准确地解答问题，并掌握相应题型的解答规律，这样才能为中考函数应用题的解题提供帮助.

2 把握解题细节，进行类比分析

在对函数应用题进行解答时，把握解题的细节，并巧妙进行类比分析是解答函数应用题时一个十分重要的技巧和方法.常用的类比分析就是指在解题的过程中，引导学生回顾与该题型相似的题目，然后探寻二者之间的联系，根据类型模拟曾经的解题方法，从而快速解决问题.在实际教学中，这种解题方法通常也被称为“变式训练”，能达到举一反三的教学效果.但要想运用好这种解题方法，初中数学教师还必须引导学生细致分析该类型题目解题的思路，把握解题的细节，了解应注意的事项，如函数自变量的取值范围、函数的值域等，切不能一味生搬硬套，导致解题错误.

例如，在教学浙教版初中数学九年级上册第一章《二次函数》第三节《二次函数的性质》的内容时，作业部分第6题：篮球运动员投篮后，篮球运动的路线为抛物线的一部分，抛物线的对称轴为直线x=2.5，求(1)球运动路线的函数表达式和自变量的取值范围；(2)球在运动中离地面的最大高度.

在讲解这道题时，教师就可以引导学生回顾上一节数学课作业题中的第5题，运动员推铅球的问题，回想教师在讲解这一道题解题的思路和方法，然后把握解题的细节，根据题目给出的数据，并结合教材给出的图示，设出未知量，并找到等量关系，求出抛物线的方程式，最后再求出未知量.

3 巧用转化思维，实现数量转换

初中学生在解答函数应用题时，往往会因为思路不清或者是对未知的参数理解错误导致解答错误，时间一长，就会打击到他们学习的积极性和自信心，这样到了中考时，面对函数问题，就会影响到他们实力的发挥，进而影响到中考答题.面对这一问题，初中数学教师应加强对学生的指导和点拨，引导他们巧用转化思维，实现数量关系的转换，如运用逆向思维进行思考，将未知的参数变成已知数，把变量当作常量，通过这样的数量转换，降低解题的难度，正确解答函数问题，逐渐培养学生学习的自信心，丰富他们解题的技巧，提升他们解题的能力.

例如：已知x1和x2是关于x的方程(x-2)(x-m)=(t-2)(t-m)的两个实数根.(1)求x1和x2的值；(2)若x1和x2分别是某直角三角形中两直角边的边长，当实数m和t满足什么条件时，该直角三角形的面积最大？求出其最大值.

在引导学生解答这道函数应用题时，如果学生们直接入手分析实数m和t，几乎是无法进行解答的，只会让他们陷入思维混乱当中，从而影响到答题的准确性.数学教师可以引导学生，将问题中的实数m和t当成常量，可以以其中的一个常量对x进行求解，找出x与实数m和t之间的关系式.

4 利用函数图像，做到数形结合

在初中函数应用题解答时，教师还可以巧妙利用函数图像，引导学生进行数形结合，这也是提升学生解题能力，将函数问题解答落实到中考当中的有效措施.在实际应用中，利用函数图像，做到数形结合，能有效降低函数应用题解题的难度，帮助学生更快、更准确地解答出正确的答案.

例如，已知抛物线y=x2-2x+c的部分图象如图2所示.

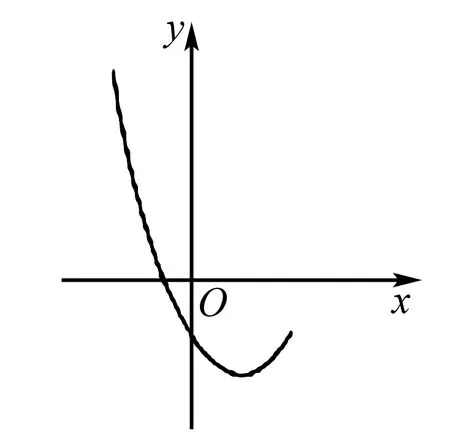
图2

(1)求c的取值范围；

(2)若抛物线经过点(0，-1)，试确定抛物线y=x2-2x+c的解析式.

这道函数应用题就是一道典型的蕴含着数形结合思想的题目，在解答这道题时，需要学生在解题的过程中，认真审视题目中所给出的数据及图像，细心把握住图像给出的信息及其囊括的相应知识点，然后认真分析，运用数形结合的思想，解答出每一个未知的参数.此外，教师还要引导学生在解出答案后，回过头来对题目所给的图像再一次进行分析，细心排除掉图像中不可能存在的情况，从而提高自己的答题准确率.只有这样做好数形结合，才能真正有效提升学生的解题能力，为他们中考取得高分奠定基础.

5 巧用几何画板，建立动态思维

与以往的教学相比，几何画板可以使原来静态的函数图像动起来，从而能够给学生更加直观的了解到二次函数的解析式与函数图像之间的对应关系.例如，在学习图像变换的相关内容时，教师可以利用几何画板动态展示二次函数y=2x2图像到y=2(x+1)2+4图像的变化，而在以往的函数教学中，教师通常的做法只能是在黑板上画出静态的函数图像，然后让学生进行观察比较，但往往人工作图会出现误差，不太标准的图形很难收到理想的教学效果.在二次函数的教学中，几何画板还能进一步对所学知识进行更深入的探究，辅助学生对二次函数性质的理解和归纳，几何画板中的移动、计算、隐藏、系列等功能，能使教学活动更加生动形象，学生的数学理解力更强，教学效率更高，同时，学生有了动态图的直观感受后对题目的分析也会更全面，从而加深对函数的理解，提高解决函数问题的能力.

综上所述，在初中数学教学中，函数知识是教学中重要的内容，也是中考数学试卷必出的题型.在实际教学中，函数知识的内容比较丰富，解答起来具有一定的难度.作为初中数学教师，应在日常的教学中想方设法将其落实到中考中，结合中考的要求，让现代信息技术作为辅助手段，教会学生找等量关系，提取题目中的隐含信息，然后再通过对其他条件的分析，提高学生解题和分析的能力，从而为学生的全面发展奠定坚实的基础，同时也为后续的更复杂的函数学习做好准备.