研究一个圆锥曲线的难点
——解析几何中向量最值
贺凤梅
(新疆伊犁巩留县高级中学 835400)
1 试题呈现
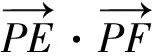
A.3 B.4 C.5 D.9
2 总体分析
此题是2021年9月的一道高三调研试题,题干简洁,解法灵活,不同的解法思维量不同,运算量不同,算得上是一道经典题目. 我发现很多学生解答此题仅停留在很基本的认知阶段,相当多的学生又因为计算不过关等原因不同程度卡壳,无法完成解答. 笔者试着将此题进行全方位剖析和解答,以期达到抛砖引玉之功效.
3 试题解答
解法1圆C的圆心为C(2,0),半径r=2.
当EF所在直线的斜率存在时,设直线方程为y=k(x-2),
代入(x-2)2+y2=4,得
(x-2)2+[k(x-2)]2=4.
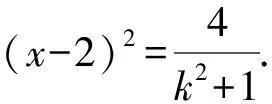
设E(x1,y1),F(x2,y2),不妨设x1 ① ② ③ 将①②③代入整理,得 所以x0=-1时,f(x0)取最小值,且为5. 当EF斜率不存在时,方程为x=2. 则E(2,-2),E(2,2),P(x0,y0). 评注因为直线过已知点,可设直线的点斜式方程,联立方程组,求出交点坐标,再利用向量的数量积转化得出关于x0的二次函数,最后利用单调性求出最小值. 此解法看似思路自然,比较符合学生的认知规律,但从呈现的解题过程来看,基本上是一道解答题的运算量,从严密性的角度来看,还要考虑斜率不存在的情况. 所以作为选择题这样求解,的确得不偿失. 解法2根据直线EF过点C(2,0),可设直线方程为x=my+2,代入(x-2)2+y2=4,得 [(my+2)-2]2+y2=4. 结合解法1,整理求解同样可得 评注此解法所设方程为直线的横截式,可以避免讨论斜率是否存在的情形,但计算量仍然不小.那么,有没有简单的求解方法,实现小题小解呢? 解法3由向量加法的三角形法则,得 因为EF为圆C的直径, 解法4 由向量的减法,得 结合解法1,得 下同解法1. 设P(x,y),则x2-y2=1. =(x-2)2+y2-4 =2x2-4x-1. 令g(x)=2x2-4x-1,x≤-1, 结合解法1可知, x=-1时,g(x)min=g(-1)=5. 学术研究一向存在两种具有辩证色彩的现象,可以分别称为“大题小作”和“小题大做”。所谓“大题小作”,就是面对重大的、牵涉面广的研究课题,研究者要善于突出重点、提炼精华,避免巨细兼顾、失之杂芜;所谓“小题大做”,就是面对涉及的领域相对狭窄的研究课题,研究者要善于以研究对象为基点和核心做横向拓展,善于勾连和比较,使立论扎实、内涵丰厚。尚继武的专著名为《〈聊斋志异〉叙事艺术研究》,但所论内容不限于《聊斋志异》,也不限于“叙事艺术”,内容丰富,视野开阔,可以称得上是一本“小题大做”的著作。 评注此解法利用向量实现转化后,再结合二次函数求最值,方法简单可行,学生也容易掌握. 下同解法1. =(x-1)2+y2-4 所以x=-4时,g(x)max=g(-4)=21; x=4时,g(x)min=g(4)=5. 解法4由解法1或解法2可得 =cos2α-8cosα+12. 令g(cosα)=cos2α-8cosα+12, 而-1≤cosα≤1, 所以g(cosα)=cos2α-8cosα+12在cosα∈[-1,1]上单调递减. 所以cosα=-1时,g(cosα)max=g(-1)=21; cosα=1时,g(cosα)min=g(1)=5. 解圆锥曲线和平面向量交汇题的方法通常有代数法和几何法.代数法的关键是设点的坐标,将平面向量用坐标表示,运用向量的坐标运算法则(加、减、数乘)、运算律及数量积的意义,最终转化为代数关系;也可以利用几何法,关键是利用加法的三角形法则、向量的减法、相反向量等,当然还要结合圆锥曲线的相关性质进行运算和转化. 高中数学教学的目的,归根结底在于培养学生的理解能力和思维能力,提高解题能力是数学教学中一项十分重要的任务,始终贯穿于高中数学教学.在解题教学中,教师应该引导学生学会解题策略和方法,不断进行分析和思考,从而深化对问题的理解,真正掌握解题的本质,探索解题的思路和规律.这样做更有利于培养学生的思维品质和数学能力.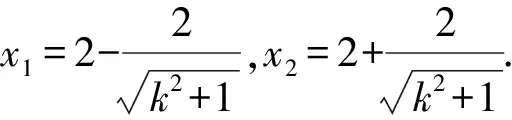
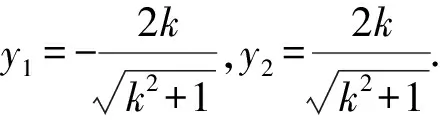

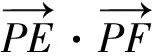
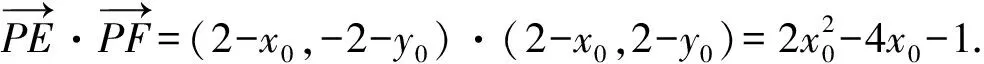
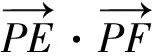
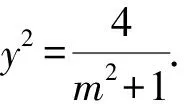
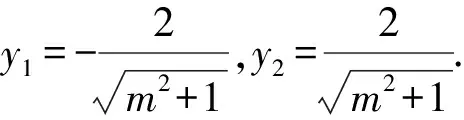
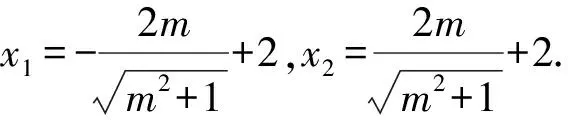
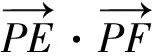
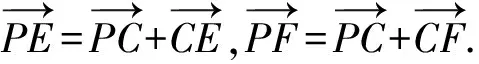
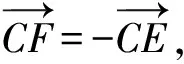
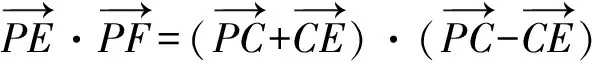
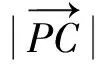

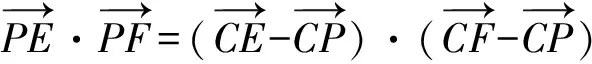
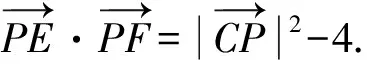
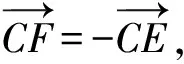
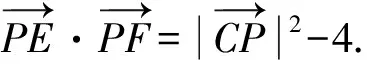
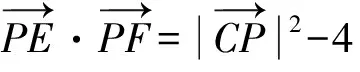
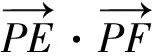
4 举一反三
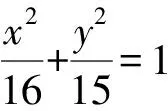
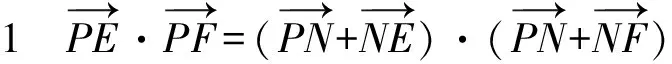
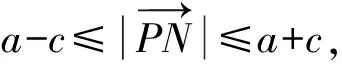

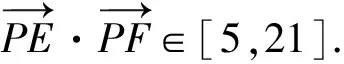
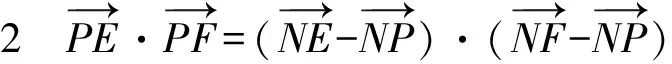
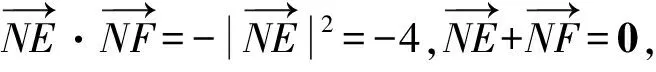
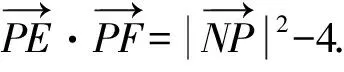
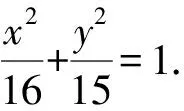
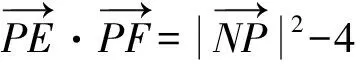
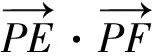
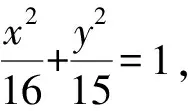
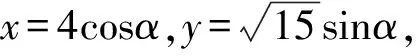
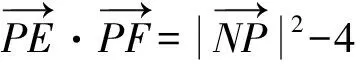
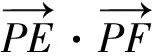
5 解题反思

