合理转化 妙设巧算——十法破解2021年成都三诊12题

李小蛟

(四川省成都市树德中学光华校区 610091)

基金项目：四川省数学会重点立项课题“提升学生核心素养的高中数学课程校本化研究”(项目编号：2020SXHJY004).

1 题目呈现

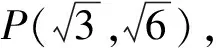
A.14 B.10 C.8 D.2

2 解法探析

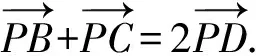
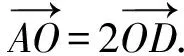
所以D(-cosθ,-sinθ).

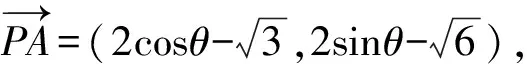
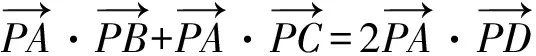
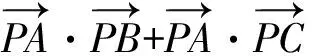
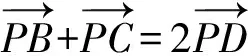
解法2 由题意，得

所以不妨令A(2cosθ,2sinθ),

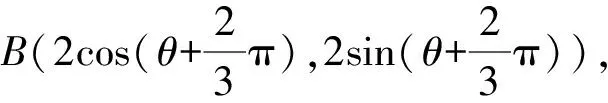
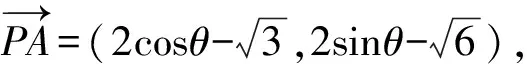
代入化简,得

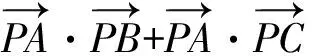
评注圆上点的坐标之间相互依存，圆心角为定值，所以直接采用圆心角之间的关系三角换元(参数方程)，直接代入化简.

解法3 由题意可得O为ΔABC的重心，

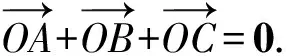
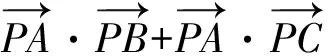
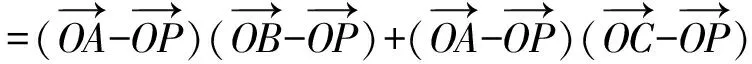
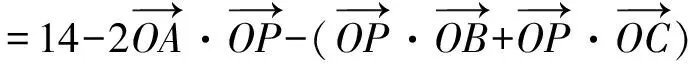
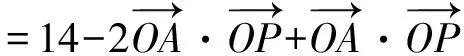
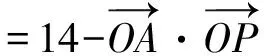
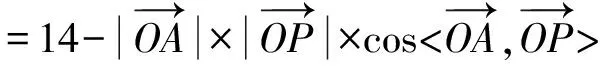
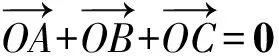
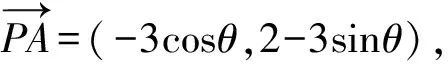
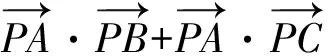
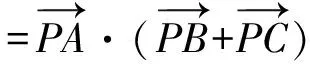
=(-3cosθ,2-3sinθ)·(-6cosθ,-2-6sinθ)

=18cos2θ-4-6sinθ+18sin2θ

=14-6sinθ≥8(当sinθ=1时取等).

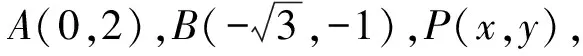
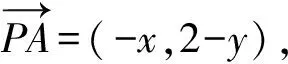
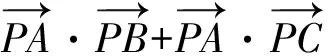
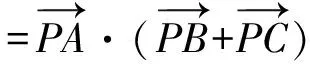
=(-x,2-y)·(-2x,-2-2y)

=2x2-4-2y+2y2

=14-2y.

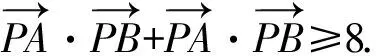
评注由于三角形上三点之间相互依存，虽位置不定但始终存在任意两点距离相等的联系，故可将三角形顶点固定，将点P看成圆上的动点，将多动点问题转化为单动点问题，再利用圆的参数方程将坐标双变量转化为角度的单变量，回归三角，减少运算，直接利用三角函数的有界性求取最值.

解法6令A(x1,y1),B(x2,y2),C(x3,y3)，由题意可得O为△ABC的重心.

故x1+x2+x3=0,y1+y2+y3=0.

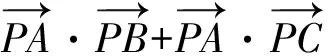
不妨设x1=2cosθ,y1=2sinθ，

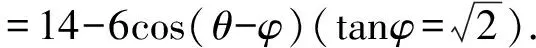
所以当θ=φ时，原式有最小值为8.

评注利用三角形重心的坐标公式将三个顶点坐标建立等量关系，将平面向量数量积回归到坐标运算，通过三顶点在圆上，进行一系列代换，转化为顶点中一点的坐标关系运算，再次利用参数方程.

解法7 由解法6，得

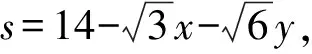
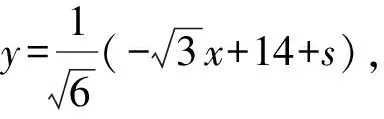
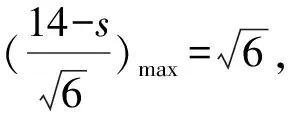
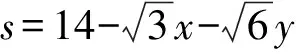
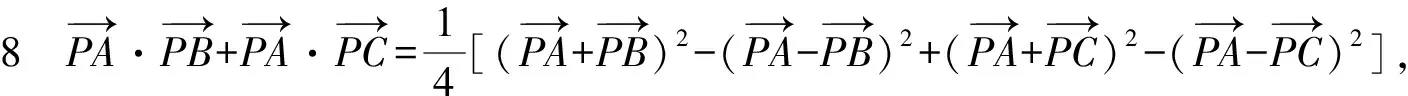
令M,N分别为AB,AC中点，Q为MN中点，

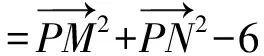
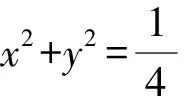
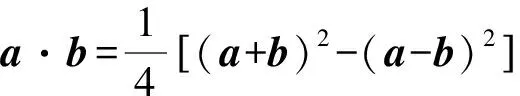
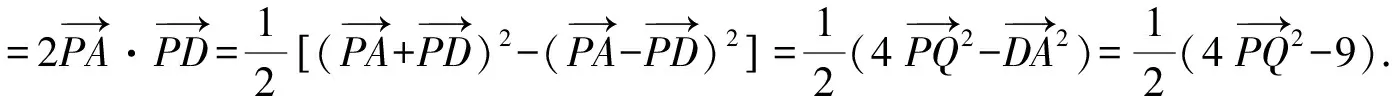
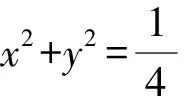
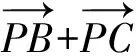
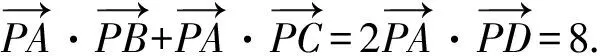
评注本题作为选择题，观察题目结构，分析题目条件和所求数量积之间关系，尽量数形结合，以形助数，做到小题小做，优化解法，提升解题效率.

平面向量的数量积一直是高考的热点问题，正确理解数量积的定义和几何意义是处理问题的关键；同时要将三角、函数、解析几何、不等式等相关知识加以迁移渗透，综合运用，注重数形结合、化归与转化等数学思想；在解题归纳上注重模型意识，合理转化，妙设巧算，才能将核心素养在解题中得到真正体现和展示.