一道联考试题的解法探究

李 亮

(安徽省蚌埠第二中学 233000)

今年五月的皖淮名校联考，高一数学试卷填空题第16题考了一道三角求值题.从考试结果来看，得分率很低.究其原因，笔者认为还是同学们对三角求值题缺乏必要的认识，方法选取不恰当，平时练的少，对复杂计算驾驭能力有待提升，值得反思.鉴于此，笔者以此题为例，和同学们一起从不同视角来探究，以期提升同学们的数学计算、逻辑推理等能力.

1 试题呈现

题目sin220°+cos250°+sin20°cos50°=____.

2 解法探究

2.1 常规思路，通性通法

解法1(遇平方就降幂，积化和差、和差化积)

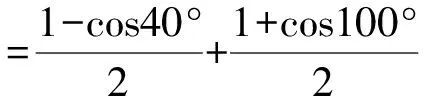
解法2(先积化和差、和差化积，再平方降幂)

原式=sin220°+sin240°+sin20°sin40°

=(sin20°+sin40°)2-sin20°sin40°

=[2sin30°cos(-10°)]2

评注本解法需要学生熟练掌握三角函数的变形降幂公式以及诱导公式，同时还要灵活运用三角函数的积化和差与和差化积公式.

2.2 对比分析，合理拆分

解法3(一般角与特殊角之间的加一加、减一减)

原式=sin220°+cos2(20°+30°)+sin20°·cos(20°+30°)

评注本解法要关注角与角之间的内在联系，把一般角与特殊角联系起来，常用技巧可以把两个角加一加、减一减、乘以2，等等，很多题目可以迎刃而解.

2.3 合情猜想，演绎推理

解法4(大胆假设，小心求证)

因为sin215°+cos245°+sin15°cos45°

猜想：

证明如下：

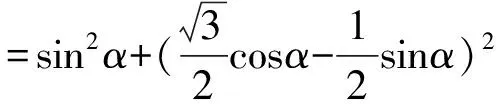
所以猜想成立，这样本题可以推广到一般形式.从而可以作以下同解变形：

sin220°+cos250°+sin20°cos50°

=sin215°+cos245°+sin15°cos45°

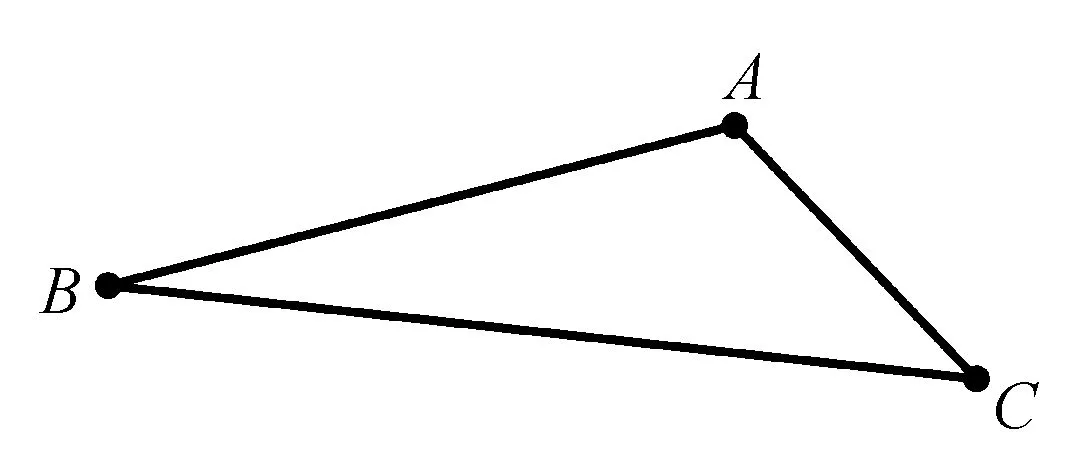
图1

2.4 结构联想，几何直观

解法5(利用正、余弦定理，构造三角形)

原式=sin220°+sin240°+sin20°sin40°，

由此联想到余弦定理

a2=b2+c2-2bccosA.

再利用正弦定理变形为

sin2A=sin2B+sin2C-2sinBsinCcosA.

到此可构造△ABC，如图1，使

A=120°,B=20°,C=40°，

则sin2120°

=sin220°+sin240°-2sin20°sin40°cos120°.

所以，

原式=sin220°+sin240°+sin20°sin40°

评注正弦定理、余弦定理是对三角形边角关系的量化刻画，解题时要仔细观察代数式的结构，合理联想，构造符合题意的三角形，可简化代数运算，发展学生思维.

2.5 对偶构造，同构变形

解法6(构造互余对偶式)

令x=sin220°+cos250°+sin20°cos50°，

构造y=cos220°+sin250°+cos20°sin50°，

则x+y=2+sin70°，

两式相加整理,得

评注通过对题目结构特征的观察，利用互余函数构造对偶式，从而独辟蹊径，出奇制胜.其实，两种对偶式的本质是一样的，利用了三角函数变换中的平方关系.

2.6 恒等变形，曲径通幽

解法7(运用三角恒等式)

由正弦与余弦的和角公式和差角公式可得以下恒等式：

sin2α-sin2β=sin(α+β)sin(α-β)，

cos2α-sin2β=cos(α+β)cos(α-β).

它们的结构和代数中的平方差公式很像，所以也把它们称之为三角函数的平方差公式.解题时灵活运用它们会使我们的化简、计算大大简化.

原式=sin220°-sin250°+sin20°cos50°+1

=sin70°sin(-30°)+sin20°cos50°+1

通过以上解法，我们可以看出三角函数的化简与求值常常从以下几个方面突破：减少函数名称、减少角的个数、注意式子的结构等.当然教材基本公式的记忆与常见变形是我们解题的基础.本题看似平常，其实值得研究，笔者只是从常规入手，多视角突破，以期起到抛砖引玉的作用，不足之处敬请大家批评指正.