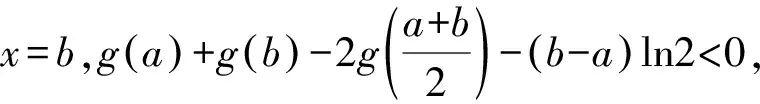例谈双元不等式证明中的减元策略
张志刚
(山东省宁阳县复圣中学 271400)
双元(例如x1,x2)不等式的证明是高考数学常考常新的命题热点,解答时往往需要适时构造新函数,借助导数工具加以讨论.鉴于高中阶段仅限于学习一元函数的导数运算及应用,因此,证明双元不等式的核心思想就是减元(消元),即将双元不等式转化为一元函数不等式去解决.如何有效地实施减元就成了解题的关键,采用何种策略要视具体题设条件而定,不可一概而论.本文以近年高考试题和模拟题为例,探讨具体题设环境下如何实施消元.
1 商式换元法
其基本原理是:依据题设条件,如出现两个齐次式之商的形式,则可以考虑将函数表达式转换成关于两元比值的单变量函数.

此方法常常用于对数函数为背景的双元不等式证明.





由切线不等式lnx 例2 已知函数f(x)=ax2-blnx在点(1,f(1))处的切线为y=1. (1)求实数a,b的值; 解析(1)a=1,b=2.(过程略) (2)因为0 所以g(t)在(1,+∞)上单调递增. 所以g(t)>g(1)=0,原不等式成立. 类比商式换元法,我们也可以依据题目条件,考虑将函数表达式转换成两元之差的单变量函数.此方法常常用于指数函数为背景的双元不等式证明. 设t=b-a(t>0), 设g(t)=t+2+(t-2)et(t>0), g′(t)=1+(t-1)et(t>0). 设h(t)=g′(t),则 h′(t)=tet>0. 所以h(t)即g′(t)在(0,+∞)单调递增. 从而g′(t)>g′(0)=0, g(t)在(0,+∞)上单调递增. 所以g(t)>g(0)=0. 2t 设f(t)=et-e-t-2t(t>0),则 所以f(t)在(0,+∞)上单调递增. 从而f(t)>f(0)=0,即原不等式成立. 当双元x1,x2是某二次方程的两根时,通过韦达定理求出x1+x2,x1x2,并考查是否为定值.若某一式(如下面例5中x1x2=1)为定值,利用此定值条件揭示的两变量间的联系,将其中一个变量用另一个变量来表示,代入相应的不等式中,以达到消元之目的.显然,本方法一般适用于导函数为二次函数的函数不等式的证明. (1)讨论f(x)的单调性; 解析(1)略. (2)由(1)知,若f(x)存在两个极值点,则a>2. 由于f(x)的两个极值点x1,x2满足 x2-ax+1=0, 由韦达定理,得x1x2=1. 不妨设x1 所以欲证不等式等价于 由(1)知,g(x)在(0,+∞)单调递减. 又g(1)=0,从而当x∈(1,+∞)时,g(x)<0. 例6已知函数f(x)=x2-x+aln(x+1),其中a∈R. (1)求f(x)的单调区间; 解析(1)略. (2)由(1)知,若f(x)存在两个极值点,则 由于f(x)的两个极值点x1,x2满足 2x2+x+a-1=0, 由韦达定理,得 =x2-(2x2-1)ln(x2+1). g(x)=x-(2x-1)ln(x+1), 设h(x)=g′(x),则 >ln1=0, 其基本原理是:在双元函数不等式中,将其中一个变量作为主元,另外一个变量作为副元(参数),从而构造一元函数来证明,达到减元的目的. 证明由于0 所以F(x)在(x1,+∞)上单调递减. 从而F(x) 令x=x2,F(x2)<0,即原不等式成立. 点评在本题确定主副元时,鉴于欲证不等式中x2出现次数较少,则首选x2作为主元,x1作为副元尝试解答.当然,有些题目两元出现次数相当时,也可考虑用主副元法. 例8已知函数f(x)=ln(x+1)-x,g(x)=xlnx.设0 证明(1)设 所以F(x)在(a,+∞)上单调递增. 从而F(x)>F(a)=0. 所以G(x)在(a,+∞)上单调递减. 从而G(x) 综上,原不等式成立. 点评本题考查了应用导数证明不等式的一个重要方法——设辅助函数法:将不等式所有的项移至不等式一侧,另一侧为0,然后构造辅助函数,按部就班解答即可.但本题中的不等式是双变量不等式,就需考虑选择一个元作为主变元,另一个作为参数了.例如上述解答中,即将b视为主元,将a视为副元完成证明.而在主变元的选取上,一般遵循的原则是: ①出现次数较少的字母为主变量,目的自然是为了构造函数后求导运算的便利; ②数值较大的字母为主变量,例如本例中的b.





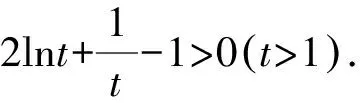


2 差式减元法
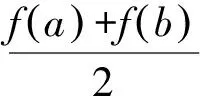








3 韦达消参法










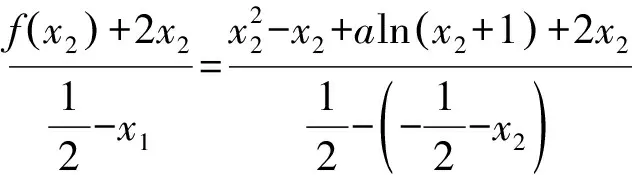





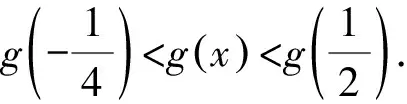
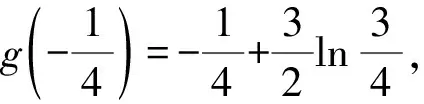



4 主副元减元法