基于时间分数阶扩散方程导数参数反演问题
彭 鑫,周晓军
(贵州师范大学 数学科学学院,贵州 贵阳 550025)
0 引言
与整数阶导数相比,分数阶微积分具有描述物质记忆功能和遗传效应的特征。分数阶微积分在电化学过程、色噪声、控制理论、流体力学、混沌、生物、工程等领域有诸多应用。例如粘弹性材料和波的传播[1-3]、无序材料中的非布朗输运现象[4]、非牛顿复杂流体和流变性[5-9]、生物组织中的多尺度模式[10-14]、混沌分形和自动控制[15-16]。
近些年来,多孔、流变、粘弹性和分形介质中的反常扩散现象引起了人们的广泛关注。对于粒子扩散过程中的随机运动,经典的Fick定律认为粒子只能在单位时间步长内跳到相邻的位置。然而,在异质介质中的许多实验观测中,粒子不仅可以跳跃到相邻的位置,而且能以较低的概率跳到更远的位置,这一非局部特征可以利用分数阶导数来刻画。分数阶微分算子凭借其特有的全局性,可以更好地描述这些反常扩散现象。例如,针对磁流体动力学模型,Tassaddiq[17]利用分数阶导数构造了一个带非奇异核的非局部算子来进行研究,实验数据表明,所得到的结果更符合实际。Sun等[18]给出了粘弹性复杂介质的分数阶Langevin方程及其反常扩散。在声波传播实验中,分数波模型与实验结果得到了很好的吻合。Xu 等[19]研究了混凝土状颗粒材料的输运特性。在微观尺度上,这种材料固有的各向异性和异质性不符合经典的菲克定律。这表明了分数阶阶数与材料结构的异质性之间有着重要联系。
在研究各种反常扩散现象过程中,分数阶微分算子的导数是未知的,只有一些实验观测数据是可用的。对于构建分数阶扩散模型而言,关键在于确定其分数阶微分算子的阶数。因此,确定模型的阶数这一反问题是很有意义的。例如,文献[20]利用实际观测数据来估计简单反常扩散模型中分数阶导数的阶数。
本文研究了时间分数阶扩散方程中分数导数阶的估计问题。首先,定义了一个带自然对数核的Caputo分数阶导数算子,推导出了时间分数阶扩散方程的分数阶导数所满足的方程,称之为时间分数阶扩散的伴随方程。其次,我们对时间离散构造有限差分格式和弱形式,再对弱形式中的半离散解进行Legendre多项式逼近得到全离散格式。然后,在源项已知这一情况下,我们利用序列最小优化法对分数阶导数进行了估计。最后,数值实验结果表明,推导出的伴随方程是正确的,迭代序列是收敛的。
1 预备知识
定义1[21]α阶Caputo分数阶导数:
定义2 带自然对数核的积分导数算子:
令T>0,Λ∈(0,1),考虑如下时间分数阶扩散方程
(1)
在接下来的讨论中,我们假定方程(1)存在唯一光滑解。
定理1 令u是(1)的解,则uα是如下时间分数阶扩散伴随方程的解
(2)

证明设u是方程(1)的解,则
对上式关于α求导,即
先对等式左端第一项进行求导,得
同理,对方程(1)左端第二项和右端源项关于α求导,得
同理,对方程(1)的初、边值条件关于α求导变为
uα(x,0)=gα(x),x∈Λ,
uα(-1,t)=uα(1,t)=0, 0 我们考虑源项f已知, 但分数阶导数的阶数α未知。为了估计未知参数α,设问题(1)的解u的测量值为z。定义二次误差函数如下 于是,最小化问题可写为: 寻找合适参数α*满足E(α*)=inf{E(α),0<α<1},众所周知其必要条件是:E′(α)=0,我们构造一个最小优化序列: (a)初值估计: 选择α0∈(0,1); (b)问题求解: 通过求解方程(1)和(2),得出u和uα; (d)参数更新:αk+1=αk-ρΔαk,其中ρ>0是一个足够小的数。 为了简化记号且不失一般性,在格式建立过程中考虑f≡0。首先考虑均匀离散(tk)0≤k≤K,时间步长h=T/K。将分数阶导数写成如下的式子: 对所有的0≤k≤K-1, 则(1)的有限差分格式为: 其中uk+1(x)是u(x,tk+1)的近似,即 (3) 对于系数wj,容易发现: (i)wj>0,j=0,1,…,k; (ii)1=w0≥w1≥w2≥…≥wk→0,k→∞。 设λ=Γ(2-α)hα,于是得到(3)的等价形式: (4) 特别地,当k=0时,格式(4)变为: (5) 于是,式(4)和(5),以及初、边值条件 u0(x)=g(x),x∈Λ, uk+1(-1)=uk+1(1)=0,k≥0 组成了一个半离散问题。 (6) 同样为了方便起见,在格式建立过程中考虑f≡0。使用如下的式子:对所有的0≤k≤K-1, 则(2)的有限差分格式为: 其中uk+1(x)是u(x,tk+1)的近似,即 (7) 特别地,当k=0时,格式(7)变为: (8) 于是,式(7)和(8),以及初、边值条件 组成了一个半离散问题。 (9) 令LN(x)为N次Legendre多项式。ξj,ωj(j=0,1,2,…,N)分别是 Legendre-Gauss-Lobatto(LGL)点和权。Legendre-Gauss型求积如下给出: 对任意的连续函数φ和ψ,其离散内积及范数定义为 (10) 其中双线性型AN(·,·)和泛函FN(·)分别定义为 (11) 其中其中双线性型BN(·,·)和泛函SN(·)分别定义为 (12) (13) hj∈PN(Λ),hj(ξi)=δi,j,∀i,j∈{0,1,…,N},其中δi,j是Kronecker函数。 对上述方程组使用离散内积定义,得 于是问题(1)和(2)的矩阵表述为: 其中Fi=FN(hi),Si=SN(hi),并且∀i,j∈{0,1,…,N}, Hij=Aij+λBij,Aij=ωiδij, 例1 考虑方程(1)其初值为g(x)=0,精确解u的观测值z为 z(x,t)=tx(1-x), 源项f定义为 其中α*=0.5给定的导数精确阶。 我们的目标是,根据已知的观测数据z,去估计精确阶α*的值。为此,采用所介绍的优化算法,给α取定初值进行迭代求解。我们取分数阶导数的初始值α0=0.7,根据所给算法利用MATLAB的编写程序并运行,得出迭代过程中导数阶的变化情况(见表1)和相应的精确阶与迭代阶的误差曲线(见图1)。 图1 分数阶导数的精确阶数和迭代阶数的误差曲线(例1) 表1 不同迭代次数下的分数阶导数的阶数(例1) 例2 考虑方程(1),假设初值g(x)=0,观测值z(x,t)=t2sin(2πx),其源项f为 同样地,本例中取初始导数阶α0=0.8,编写程序并运行,得出迭代过程中导数阶的变化情况(见表2)和相应的精确阶与迭代阶的误差曲线(见图2)。 图2 分数阶导数的精确阶数和迭代阶数的误差曲线(例2) 表2 不同迭代次数下的分数阶导数的阶数(例2) 在本文中,我们推导出了时间分数阶扩散方程的解关于分数阶导数α所满足的方程,称之为分数阶扩散伴随方程。首先,我们对两个方程进行时间离散,得出了相应的有限差分格式和弱形式。然后,我们使用了Legendre谱配置法对弱形式中的半离散解进行多项式逼近,得到全离散格式。最后,在源项f已知这一情况下,我们利用序列最小优化法对分数阶α进行了估计。数值结果表明,我们推导出的伴随方程是正确的,迭代序列是收敛的,且精度良好。2 时间离散:有限差分格式
2.1 方程(1)的有限差分格式及弱形式
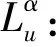
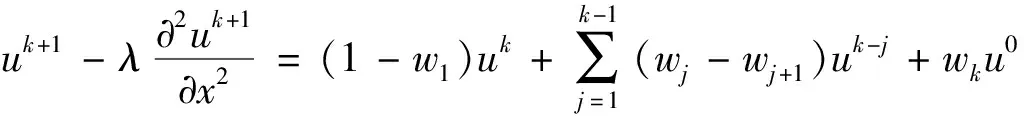
2.2 方程(2)的有限差分格式及弱形式
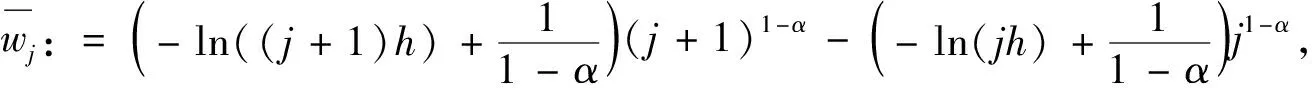
3 全离散
3.1 方程(6)的Legendre 谱配置法


3.2 方程(9)的Legendre 谱配置法
4 数值有效性
4.1 数值实施

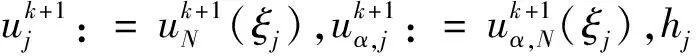
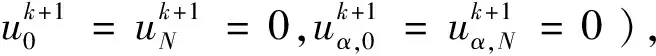
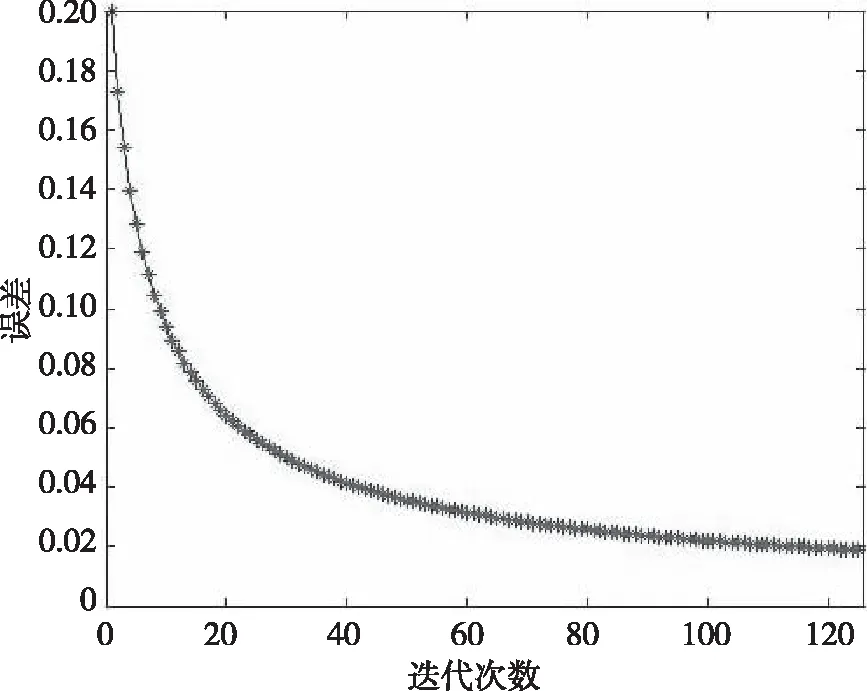
4.2 数值算例



5 总结

