忆阻自突触Hopfield 神经网络的动力学分析与电路仿真

张学丰，彭良玉，彭代鑫

(湖南师范大学 物理与电子科学学院，湖南 长沙 410081)

人脑是目前已知最为复杂的非线性系统，它除了支配运动、感觉以外，还与认知、情感、行为、语言等高级神经活动有关。对于人脑动态特性的研究，一般采用人工神经网络模型作为研究对象。Hopfield 神经网络(Hopfield Neural Network，HNN)是由多个神经元构成的一类重要的神经网络模型。由于HNN 存在特殊的非线性神经元激活函数。因此，它可以模拟人脑产生复杂的动力学行为。2005 年，Korn 教授证实了人脑中存在混沌，这就为混沌动力学研究提供了一个全新的应用前景[1]。2017 年，Panahi 等[2]提出，人脑的神经活动有时会从混沌转变为周期，这说明人脑总是处于有序和无序的交替过程中。目前已有大量关于神经动力学的研究，并在HNN 中发现了一些复杂的非线性现象，如混沌、超混沌吸引子、隐藏吸引子和暂混沌行为等[3-5]。

忆阻器具有可编程性和突触可塑性等特点，且与生物神经元突触有相似的特征。因此，科研人员使用忆阻器模拟神经元的突触，人为地控制神经网络的突触权重系数来探讨忆阻器对神经网络的动力学的影响。这就可以定量地分析忆阻突触对神经形态电路的电活动行为的影响。2014 年，李清都教授等[6]第一次用忆阻器模拟由两个神经元之间膜电差诱发的电磁感应效应，提出了一种具有超混沌吸引子的忆阻突触Hopfield 神经网络(MHNN)模型，并说明了忆阻器在探索神经网络的动力学行为方面的重要作用。2017 年，包伯成教授团队[7]提出了一种新型双曲正切型忆阻器，同样模拟由两个神经元之间突触所造成的电磁感应效应，构建了一种新型MHNN 模型，并发现该系统具有不对称的共存吸引子。这说明新型忆阻器会使HNN 产生新的复杂动力学特性。2020 年，胡义华教授团队[8]在三阶HNN 中用两个忆阻器模仿两个突触之间发生串扰的现象，并给出了HNN在突触串扰下的数学模型，发现了该系统共存多稳态现象。由此可见，忆阻突触模拟器已成为构建神经网络电路的重要组成部分。

上述文献的创新之处在于用不同类型的忆阻器或不同数量的忆阻器模拟多个神经元之间突触的电磁感应效应及突触串扰现象来研究忆阻器对HNN 的复杂动力学行为影响。这些工作都只考虑了忆阻突触对神经网络的影响，而并未考虑神经元自突触对神经网络的影响。2017 年，北京师范大学的科研人员[9]发现神经元自突触在调节人脑的信号处理方面也发挥重要作用。2020 年，王春华教授团队[10]在单欣德马什-罗斯(Hindmarsh-Rose，HR)神经元模型中引入了局部有源忆阻器来模拟神经元的自突触，发现该忆阻自突触HR 神经元存在多种放电模式和多稳态特性。因此，忆阻自突触也会对神经网络的动力学特性产生影响。受此启发，本文在三阶HNN 中引入一个非理想的磁控型忆阻器来设计一种忆阻自突触Hopfield 神经网络(MAHNN)。该忆阻器被用来模拟第3 个神经元自突触所造成的电磁感应效应。在模型中引入忆阻控制参数来控制神经元自突触对神经网络电活动行为的影响。理论分析和数值仿真表明，该模型具有一对不稳定的对称鞍焦平衡点，可产生双涡卷混沌吸引子、对称共存单涡卷或周期吸引子，还可以产生暂混沌和混沌与周期交替等特殊动力学行为。除了数值仿真，本文还设计了MAHNN 的模拟仿真电路，并给出了相应的电路仿真结果。由于MAHNN 中混沌与周期交替现象正符合人脑的神经活动有时会从混沌转变为周期的特点。因此，研究MAHNN 可以对人脑神经活动的研究提供一定的参考价值。从动力学角度去分析MAHNN 的电活动行为，有助于深入了解混沌与周期交替现象在人脑正常活动和非正常活动等方面的作用，为理解人脑功能提供神经动力学方面的解释。

1 MAHNN 的建模与基本特性分析

1.1 MAHNN 的数学模型

2015 年，蔡少棠教授详细地阐述了忆阻器理论，定义了非理想磁控型忆阻器的通用数学模型为:

式中:x表示磁通状态变量;G(x)代表忆导函数;v、i分别表示忆阻器两端的电压、流经忆阻器的电流。

根据(1)式，设计一种非理想三次磁控型忆阻器模型，其表达式为:

式中:φ为忆阻器内部的磁通量;W(φ)为忆导函数。

在文献[11]三阶HNN 的基础上，将上述忆阻器用来模拟三阶HNN 中神经元3 自突触所造成的电磁感应效应，并提出了一种MAHNN 模型，其连接拓扑结构如图1 所示。

图1 MAHNN 的连接拓扑结构Fig.1 Connection topology of MAHNN

由图1 可知，引入忆阻自突触的HNN 数学模型会发生相应的变化。用W(φ)=1+φ2替代神经元3 自突触权重系数，并引入参数k来控制自突触耦合强度，得到MAHNN 的无量纲状态微分方程组为:

1.2 耗散性分析

任意一个非线性系统要处于混沌状态，该系统的散度∇＜0[12]。对于(3)式，计算MAHNN 的散度公式为:

根据(3) 式 和(4) 式，得 到∇=-4+1.5 sech2(x)+1.2 sech2(y)+k(1+φ2)sech2(z) 。由于0≤sech2(x) ≤1，0≤sech2(y) ≤1，0≤sech2(z) ≤1，因此，∇≤-1.3+k(1+φ2) 。显 然，-1.3+k1+(φ2)＜0，即控制参数k＜1.3，才能使该系统出现混沌吸引子。

1.3 平衡点的稳定性分析

令(3)式等号左边为0，求出方程的解，得到(3)式非线性系统所有的平衡点。

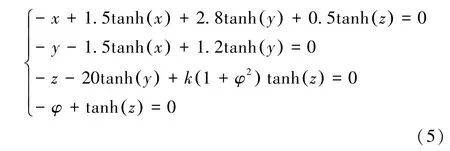
显然，(5)式是四阶超越方程组，需用MATLAB得出方程的全部解。(3)式表示的非线性系统在任意平衡点E-=(ξ1，ξ2，ξ3，ξφ) 的Jacobian 矩阵为:

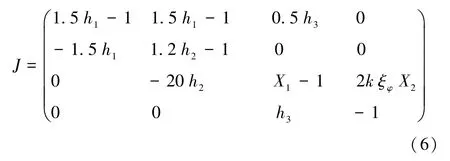
观察(5)式可知，无论k为何值时，(3)式非线性系统总是存在一个零平衡点E0=(0，0，0，0)。将E0=(0，0，0，0)代入(6)式，得到对应的特征方程为:

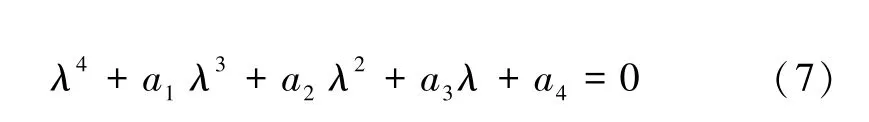
其中a1=1.3-k，a2=3.9-0.3k，a3=22.9-3.6k，a4=19.3-4.3k。

根据文献[13]中提到的Routh-Hurwitz 判定准则，零平衡点E0稳定的充分必要条件为:a1＞0，a1a2-a3＞0，a2a3-a1a4＞0，a4＞0。当满足上述条件时，可以计算出-3.504＜k＜-2.488。此时E0是稳定的。当k=-3 时，得出零平衡点的特征值λ1=-1.0000，λ2=-3.0447，λ3，4=-0.1277±0.8404i，此时E0是一个稳定的平衡点。然而，当k=-0.3 时，λ1=1.4660，λ2=-1.0000，λ3，4=-1.0330±2.3134i，此时E0是一个不稳定的鞍焦平衡点。

此外，选择合适的k值，该非线性系统还存在两个非零平衡点。在MATLAB 中，通过图形分析法可以确定x、z的数值。绘制出h1x，(z) 和h2x，(z) 的局部图形，两条曲线的交点就是x、z的数值。再根据(5)式计算出y、φ的数值。

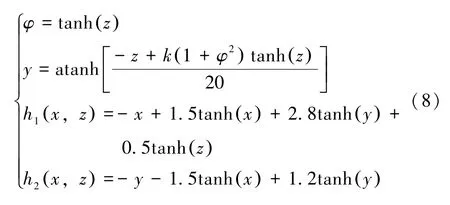
取k=-0.3 来绘制上述两个二元函数的MATLAB 局部曲线图，如图2 所示。从图中可以得到两条曲线有三个交点:E0=(0，0，0，0)，E1=(-0.0220，-0.1753，2.8781，0.9937) 和E2=(0.0220，0.1753，-2.8781，-0.9937)。用函数eig得出E1和E2对应的特征值λ1，2=0.3157±2.0004i，λ3，4=-0.9879± 0.0861i。显然，E1和E2是关于E0对称的不稳定的鞍焦平衡点，这与非线性系统(3)式关于原点对称相对应。

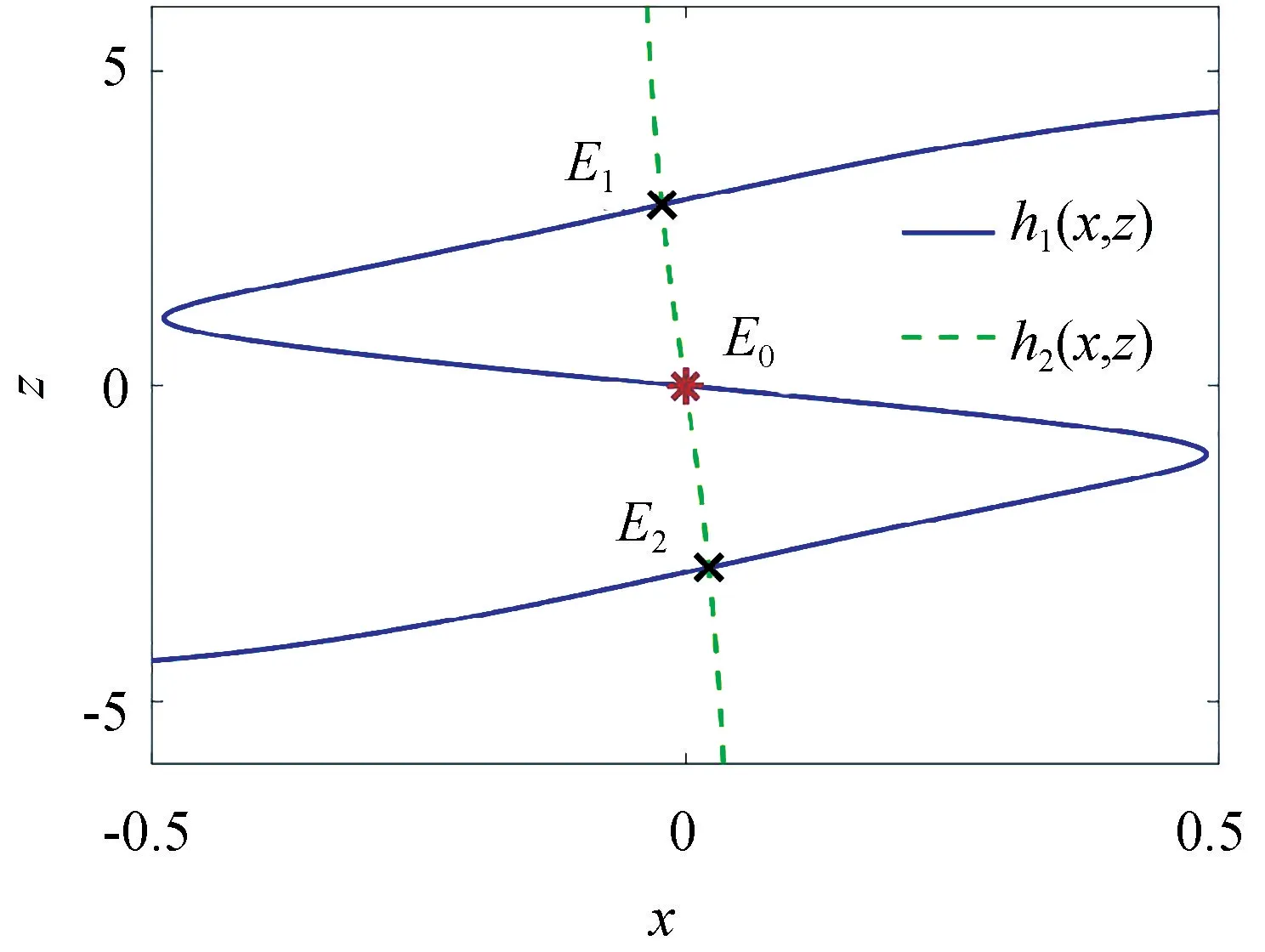
图2 两个二元函数的局部曲线图Fig.2 Local curves of two binary functions

2 MAHNN 的动力学分析

2.1 随参数k 变化的动力学行为

在(3)式中，选择参数-1≤k≤1 来分析MAHNN的动力学行为。分别设置状态变量初值为(0，1，0，0)和(0，-1，0，0)。在MATLAB 仿真平台中设定k以步长0.001 从-1 逐渐增加到1，绘制出该系统随k变化的分岔图和有限时间李氏指数图如图3 所示。图3(a)中红色“.”轨迹代表状态初值为(0，1，0，0)的分岔图，蓝色“*”轨迹则代表(0，-1，0，0)的分岔图。由图3(a)可以看出该系统存在共存分岔行为。这说明随状态初值的变化，权值不变、参数不变的MAHNN会出现共存吸引子，而这种现象正是由该系统关于原点对称引起的。从图3(b)则可以看出:系统所处的状态总是随参数k变化而在周期与混沌之间变化。因此，可以直观地从图3 中选取各种动力学行为所对应参数值。

然而，从图3 可以发现分岔图和李氏指数图并未完全对应，特别是参数-0.42＜k＜-0.37。从图3(a)可知，该系统在此区间为混沌状态。而根据图3(b)可知，最大Lyapunov 指数L1在此区间等于0，表明MAHNN 非线性系统处于周期状态。因此，在参数k处于-0.42＜k＜-0.37 时，系统状态还需进一步分析。

图3 随控制参数k 变化的动力学分析。(a) 分岔图;(b) 李氏指数图Fig.3 Dynamic analysis with control parameter k.(a) Bifurcation diagram;(b) Lyapunov exponents diagram

下面给出不同k值下状态变量x-z相图如图4所示。

图4 中红色实线、蓝色虚线轨迹分别代表状态初值为(0，1，0，0)和(0，-1，0，0)的相图。显然，随着参数k的变化，MAHNN 的吸引子形状和位置均会发生改变，进而呈现复杂多变的动力学行为。

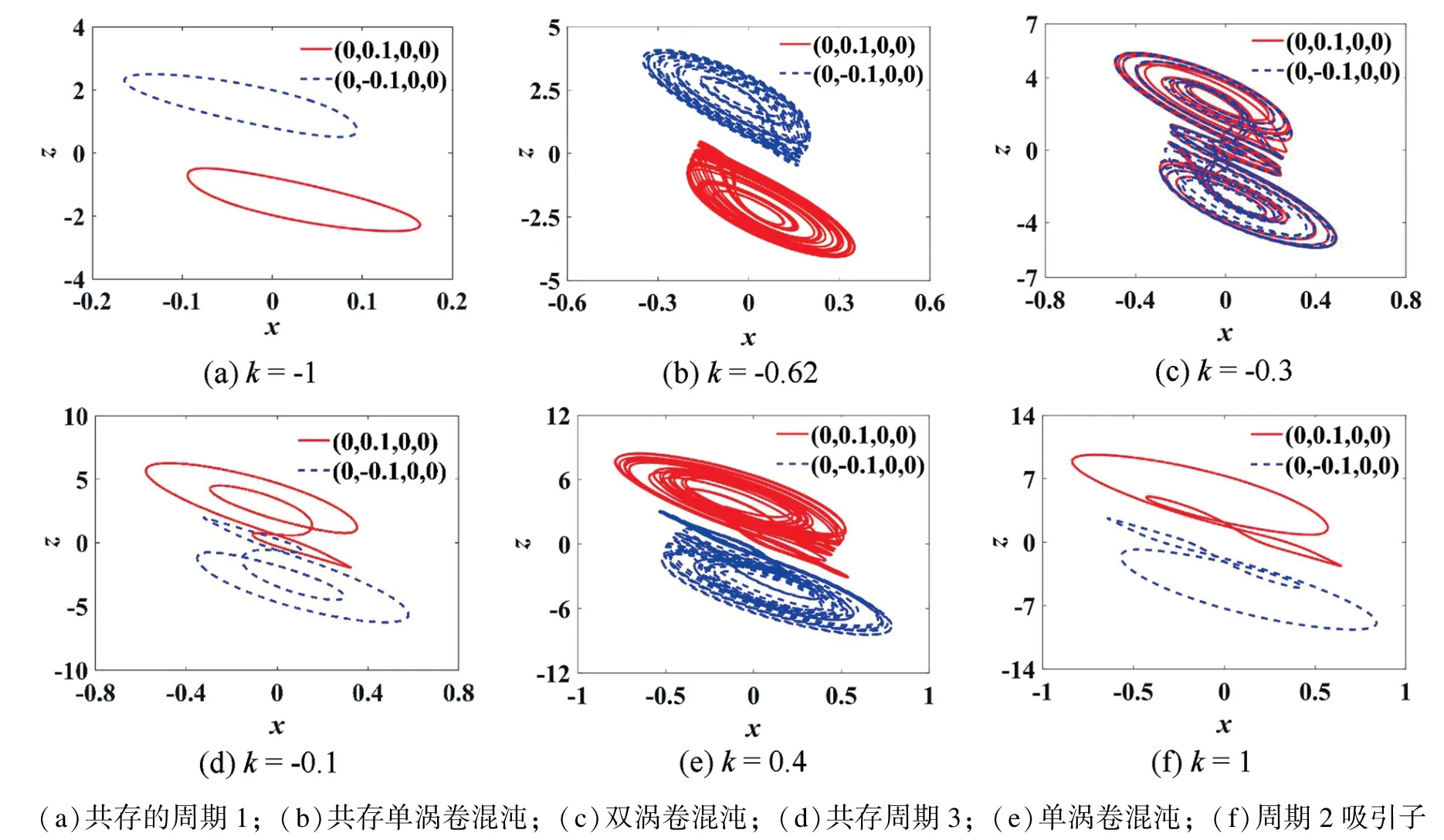
图4 典型x-z 相图Fig.4 The typical phase portraits on x-z plane

2.2 暂混沌和混沌与周期相互交替出现的现象

在2.1 节中，已提到k在-0.42＜k＜-0.37，系统状态需要进行详细的分析。因此，增加仿真时间来确定系统状态。设定该系统的仿真时间为20 ks，取k分别为-0.41 和-0.39 来具体分析该系统的动力学行为。

当k=-0.41 时，得到该系统状态变量z的部分时域图以及对应的x-z相轨迹图如图5 所示。

从图5 可知，系统先从混沌状态逐渐过渡到周期状态，并最终稳定在周期极状态，即暂混沌现象。通过MATLAB 编程，计算出Lyapunov exponents 为:L1=0.0042，L2=-0.2111，L3=-0.4702，L4=-0.8787。依据文献Lyapunov 维数计算方法[14]，得出DL=1.0199，表明该系统处在周期状态。

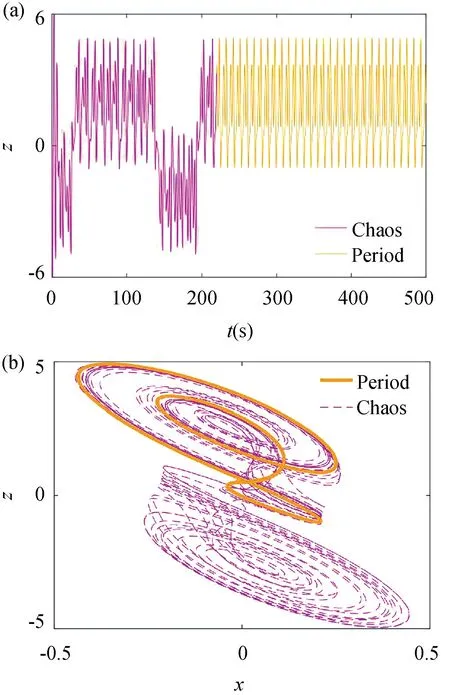
图5 暂混沌现象。(a) 时域图;(b)x-z 相轨迹图Fig.5 The phenomena of transitent chaos.(a)Time domain diagram;(b) x-z phase trajectory diagram

当k=-0.39 时，得到该系统状态变量z的部分时域图以及对应的x-z相轨迹图如图6 所示。

根据图6 可知，系统先从周期状态过渡到混沌状态，经过一段时间再过渡到另一种周期状态，并且这两种周期状态转换均是通过混沌状态(过渡状态)来实现的。随着时间演变，这种混沌与周期相互交替出现的现象会不断循环往复地进行。通过MATLAB 编程，计算 出Lyapunov exponents 为:L1=0.0380，L2=-0.0001，L3=-0.6963，L4=-0.8913，计算出DL=2.0544，表明系统仍然处于混沌状态。

图6 混沌与周期相互交替出现的现象。(a)、(b)、(c)时域图;(d)x-z 相轨迹图Fig.6 The phenomena of chaos and cycle alternation.(a，b，c) Time domain diagram;(d) x-z phase trajectory diagram

然而，目前只在引入分数阶局部有源忆阻器的忆阻Jerk 多稳态混沌系统中发现有混沌与周期相互交替的现象[15]。这种混沌与周期相互交替的现象与经常被发现的暂混沌、暂周期[16]有所不同。经查阅文献可知，这种独特的现象在Hopfiled 混沌神经网络中还未出现过。

3 MAHNN 的电路设计及仿真

为验证忆阻自突触Hopfield 神经网络的复杂动力学行为，采用改进型模块化电路的理念设计出MHANN 的模拟仿真电路如图7 所示。该电路主要由四路模拟运算电路组成，分别实现公式(3)中的状态变量x、y、z、φ的数学运算。该电路涉及到反相加法、反相积分、反相电路、忆阻器仿真电路和神经元激活函数电路单元模块。图7 中蓝色虚线圆内的SC1、SC2、SC3代表神经元激活函数-tanh(·)的子电路模块[8]，SC4代表忆阻器仿真电路的子电路模块。

该电路实现需要用到的电路元器件有集成运算放大器TL082CD，其供电电压为±15 V，饱和电压为±13.5 V，三极管MPS2222，模拟乘法器AD633，其增益为0.1。根据基尔霍夫电流定律，由仿真电路图7可得到MAHNN 的电路状态方程为:

图7 MAHNN 的Multisim 仿真电路图Fig.7 Multisim simulation circuit diagram of MAHNN

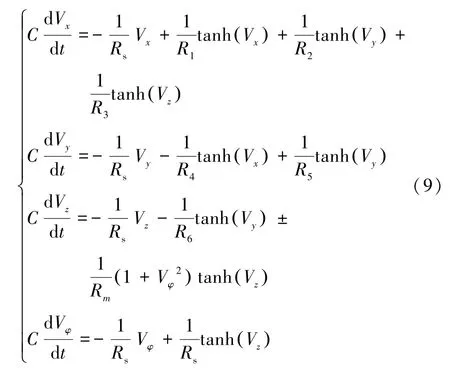
图8 中Vx、Vy、Vz分别代表三个积分器电路电容上的电压变量，Vφ代表忆阻器Memristor 内部积分电路电容上的电压变量，τ=RsC代表积分电路的时间常数。设置τ=0.1，固定电阻Rs=1 MΩ，电容C=C1=C2=C3=C4=0.1 μF，电阻R=10 kΩ。根据(3)式和(9)式，得出R1=Rs/1.5=666.67 kΩ，R2=Rs/2.8=357.14 kΩ，R3=Rs/0.5=2 MΩ，R4=Rs/1.5=666.67 kΩ，R5=Rs/1.2=833.33 kΩ，R6=Rs/20=50 kΩ。

在Multisim 的交互式仿真一栏设置初始值由用户自定义，仿真最大步长为0.01 s。设置不同的初始值对系统进行仿真，即可得到用户所需的不同数据。由于MAHNN 只受参数k和状态初值的影响，因此仿真电路只需考虑开关S、电阻Rm和电容上的电压对仿真结果的影响。开关S 在1 处接通，代表(9)式中1/Rm的系数为负，否则为正。电阻Rm=Rs/ |k| MΩ 是一个随参数k变化的电阻。对(3)式进行数值仿真时，系统状态初值(x0，y0，z0，φ0)=(0，±1，0，0)，因此设定4 个电容的电压初值为(0 V，∓1 V，0 V，0 V)。开关S 在1 处接通，分别取k为-1，-0.62，-0.3，-0.1，则 相 应 的Rm为1，1.61，3.33，10 MΩ，选择开关S 与2 处接通，取k为0.4，1，则相应的Rm为2.5，1 MΩ。对比图4 和图8，Multisim 电路仿真的相轨迹图与数值仿真相轨迹图一致，说明了忆阻自突触Hopfield 神经网络理论分析和仿真电路设计的正确性。

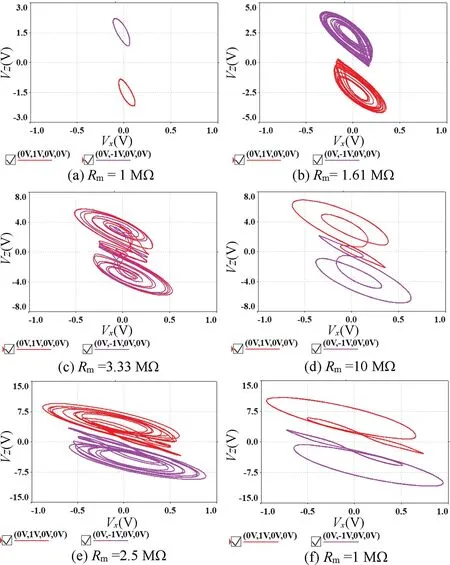
图8 MAHNN 的Multisim 相图Fig.8 Multisim phase portraits of MAHNN

5 结论

本文采用非理想磁控型忆阻器模拟3 阶Hopfield神经网络的第3 个神经元自突触的电磁感应效应，提出了一种忆阻自突触Hopfield 神经网络模型。理论分析和数值仿真表明，该模型在确定的忆阻控制参数下存在两个不稳定的对称鞍焦平衡点，这可使该系统产生一对共存的混沌或周期吸引子。忆阻器独特的非线性使得引入忆阻自突触的HNN 还会出现混沌与周期交替的特殊现象，而这种现象目前只发现在引入分数阶局部有源忆阻器的Jerk 混沌系统中。前者较后者的显著区别在于它出现在人工神经网络中，而它的发现也正符合人脑的神经活动有时会从混沌转变为周期的特性。因此，研究忆阻自突触神经网络可以为人脑神经活动的研究提供一定的参考价值。从动力学角度分析忆阻自突触神经网络的电活动，有助于深入了解混沌与周期交替现象在人脑正常和非正常活动等方面的作用，为人脑功能的理解提供神经动力学方面的解释，进而为治愈脑疾患者提供研究思路。最后，对MAHNN 模型进行模拟等效电路设计，并通过Multisim 电路仿真对其动力学行为进行了验证。仿真结果与数值仿真基本吻合，验证了MAHNN 理论设计的正确性。