基于遗忘效应忆阻器的LIF 神经元电路研究

杨宁宁，王 达，吴朝俊

(1.西安理工大学 电气工程学院，陕西 西安 710048;2.西安工程大学 电子信息学院，陕西 西安 710048)

人工神经网络的研究在各个领域已取得巨大进展，解决了实际应用中存在的很多问题。目前神经网络算法大多数运行于计算机上，在这种运行方式中，计算机的存储功能和计算功能相分离，这就导致了存储墙的存在和冯·诺依曼瓶颈，使得神经网络的计算速度大幅下降。然而在这个大数据时代，各种数据呈爆发式增长，对神经网络的运算速度也有了更高的要求。构建一个存算一体的新型神经网络可有效解决“存储墙”问题和冯·诺依曼瓶颈[1-3]，而忆阻器的提出和发现让上述神经网络的实现有了希望。

1971 年，“忆阻器之父”蔡少棠教授在理论上提出了忆阻器的概念[4]，惠普实验室在2008 年宣布物理制备了具有忆阻特性的二端元件[5]。这一突破性的研究引起了学术界和工业界的广泛关注，同时引起了基于忆阻器的神经网络研究热潮。自惠普实验室制备实物忆阻器以来，基于各种材料的忆阻硬件相继被成功制备[3，6-7]。在电路仿真中，如何用模型来描述各种忆阻器的特性也是一种极其重要的工作，Strukov 教授[5]提出了线性忆阻模型，但仅考虑了线性的氧离子迁移;2013 年和2015 年，Kvatinsky 教授提出TEAM[8]和VTEAM[9]模型;2013 年，Yakopcic 提出一个一般化的忆阻器SPICE模型[10]，Ling 提出具有遗忘效应的忆阻器模型[11];2014 年，Carbajal 提出了适用于机器学习、可模拟动态波动性的忆阻模型[12];2017 年，张洋提出一个适合于神经网络突触计算的忆阻器模型[13]。文献[14]对上述忆阻器模型进行了对比和分析，均不满足忆阻神经元电路的设计要求，可以说得到符合实际而又适合神经网络的忆阻器模型是神经网络研究的基础。因此，本文借鉴前人的研究基础，研究了一种具有遗忘效应且满足忆阻神经元设计要求的忆阻器模型。

在神经网络方面，通过研究可知在人大脑中有超过1000 亿个神经元，而且每个神经元大约有超过2 万个突触连接[15]，在神经网络电路设计中，高效、准确的神经元结构和突触结构至关重要。1988 年Chua 和Yang 提出细胞神经网络(Cellular Neural Network，CNN)[16-17]，它是一种模拟非线性、实施并行处理的阵列结构，具有连续实时、可实现高速并行处理、适用于超大规模集成电路的特点，CNN 在模式和图像分析、垂直线检测、降噪处理、目标边缘检测和字符识别等方面都具有广泛的应用[18-19]。CNN 优异的性能引起了越来越多的研究人员的关注，忆阻神经网络就是借鉴了CNN 的结构而生，用忆阻神经元代替每个细胞，成为一种新的神经网络。

一个简洁而又集成所需功能的人工神经元是构建神经形态计算系统必不可少的元素，然而目前关于人工神经元的研究进展非常有限。惠普研究人员构建了一个带有两个Mott 忆阻器的可扩展神经元，并实现了由尖峰阈值信号驱动的Hodgkin-Huxley 轴突[20]。2016年，IBM 研究人员使用相变效应忆阻器实现了具有积分和激发功能的人工随机神经元[21]。在这个神经元中，局部分级电位由相变效应忆阻器的非易失性电导表示，因此不能实现局部分级电位的短期特性，即如果神经元在某个时间接收到低于忆阻器阈值的信号，那么它的膜电位将永远保持既有状态不会改变，直到神经元被激活。这种特性明显不符合神经元行为在生物系统中的表现，在生物神经系统中，未收到输入刺激时神经元膜电位应逐渐降低，因此，可以通过在这种神经元结构上添加一个“泄漏”项来解决这种问题，即构成LIF(Leaky Integrate-and-Fire)神经元[22]。根据这种原理，本文设计了一种具有泄漏功能的神经元电路，使得膜电位在无输入的情况下逐渐下降，与神经元在生物系统中的表现相似。

为了得到符合忆阻神经元要求的忆阻器模型，解决神经元特性不符合在生物系统中表现的问题。本文基于张洋的忆阻器模型[13]，研究了具有遗忘功能的忆阻器数学模型，拟合了SrTiO3(STO)实物忆阻器的参数，并使用该忆阻器设计了LIF 神经元电路。神经元的不应期为85 μs，可反映宽度为4 μs 的输入脉冲，与其他神经元相比提高了计算速度，同时也验证了该电路可实现对时间和空间信息的整体反应。

1 忆阻器模型

1.1 积分和泄漏的忆阻器模型

LIF 神经元都具有三个基本的处理模块，即积分、泄漏和激活模块，忆阻器的机制刚好可满足这些需求。在积分和泄漏模块引用文献[14]提出的模型，如式(1)所示。ω(t)代表掺杂区宽度;R(t)代表忆阻器阻值;D是忆阻器的厚度;μv表示平均离子漂移率;RON和ROFF分别为掺杂区完全掺杂和完全未掺杂时忆阻器的阻值;p是一个正整数;v(t)和i(t)分别为忆阻器两端电压和流过忆阻器的电流。

然而在该模型中，阻值变化速度与电流成反比，也就意味着当电压越大，阻值变化越慢，实际阻值的变化恰好与此相反。上述模型使用的Joglekan 窗函数可很好地模拟状态变量未到达边界时的近似线性离子漂移情况，它较多使用于理想忆阻器模型。但Joglekan 窗函数会使忆阻非线性模型存在末端状态问题[23]，即当掺杂区和未掺区之间的分界面漂移至忆阻器的边界处后(ω(t)=0 或ω(t)=D)，忆阻器将永远保持既有状态而无法恢复，即使施加反向电压也无法改变其阻值。

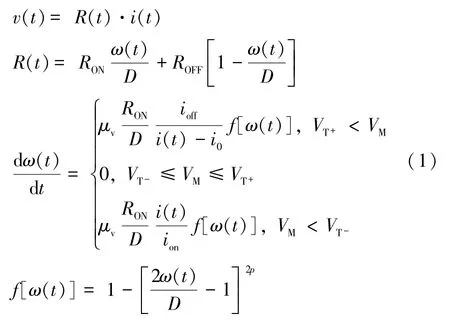
Biolek 窗函数[24]可较好地解决末端状态问题，该窗函数除了状态变量x和p外，还考虑了流经忆阻的电流，使得忆阻掺杂区和非掺杂区的分界面到达边界点后不会锁定在既有状态，流过反向电流即可改变其阻值，使其正常工作。数学表达式为:

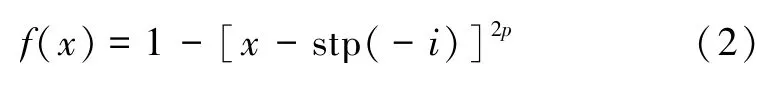
式中:p为一个正整数，称为函数的控制参数，x∈(0，1)，stp(·)为阶跃函数，且有:

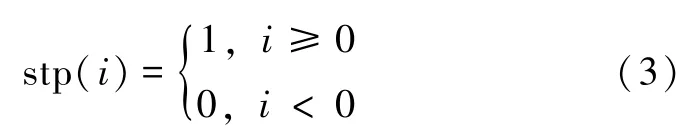
文献[25]制备了一种两端结构为Pt/STO/Nb-STO(Nb 掺杂的STO)的忆阻器，其中Pt 和导电Nb-STO 单晶分别作为顶部电极和底部电极。观察STO 薄膜和STO/Nb-STO 界面的透射电子显微镜(TEM)图像，并分析了电导随施加电压变化的特性，结合实际应用与STO 忆阻器实际变化特性，将窗函数修改为:

研究组患者治疗后睡眠质量恢复情况优于对照组，差异有统计学意义（x2=6.318，P=0.012），见表1。

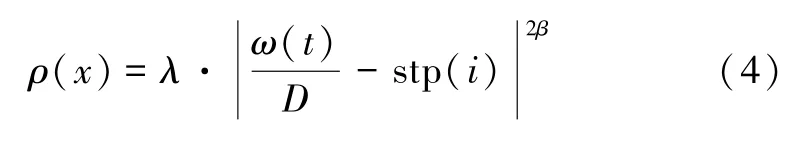
式中:λ和β均为参数变量。文献[14]提出的忆阻器模型，当两端电压小于阈值电压VT时，会有dω(t)/dt=0，即ω(t)大小保持不变，从而忆阻器阻值将保持在一个固定值。而STO 忆阻器具有二阶遗忘效应，当忆阻器两端施加电压小于忆阻器阈值电压时，其电导将随时间逐渐减小。

在上述模型基础上，本文对模型进行了相应的修改，以表现出STO 忆阻器在实际阻值变化中的特性。当忆阻器两端施加电压小于阈值时，掺杂区宽度将逐渐降低，从而阻值将逐渐变大，因此采用一个随ω(t)倍数变化的θ(t)，如式(5)所示。

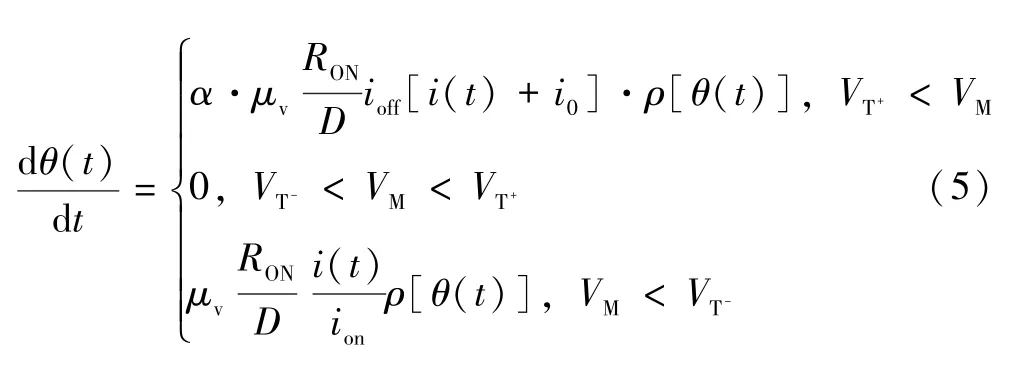
式中:α决定遗忘程度;θ(t)同为状态变量，当施加电压为正电压时，θ(t)变化速率为ω(t)变化速率的α(α＜1)倍。由于θ(t)较ω(t)变化速度慢，两者之间存在差值，该差值可表示遗忘过程中的遗忘程度。当施加大于负阈值的负电压时，θ(t)与ω(t)变化速度相同，会有θ(t)-ω(t)=0，此时阻值不会随时间变化，因此ω(t)可表示为:

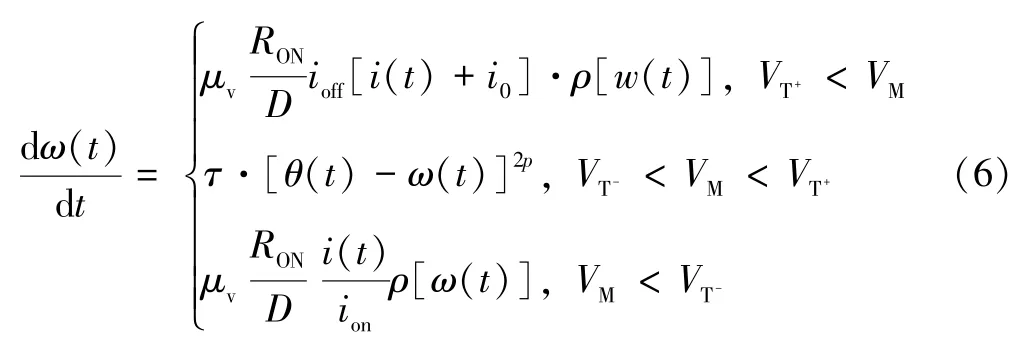
式中:τ为遗忘速度。当施加小于阈值的电压时，有dω(t)/dt＜0，ω(t)逐渐减小，阻值将逐渐增大。

图1 所示为修改后忆阻器模型对STO 忆阻器的仿真结果，根据STO 忆阻器特性的实测数据[25]，当施加正向电压(1.62 V)时，忆阻器电导值逐渐增加，变化趋势为先快后慢。施加大于负阈值的负向电压(-1.8 V)时，忆阻器电导值逐渐变小，变化趋势也是先快后慢。在仿真过程中拟合参数设定为:RON=0.43 GΩ，ROFF=1.3 GΩ，VT+=1.2 V，VT-=-1.2 V，ion=1，ioff=0.9，i0=5×10-9，λ=0.9，β=0.62，μv=0.16×10-12，α=0.79，τ=0.2×10-6，p=0.54。在忆阻器两端施加图1 所示的电压激励时，得到电导随时间变化的图像如图2(a)所示。在忆阻器两端施加幅值为1.7 V，频率为100 Hz 的正弦电得到该忆阻器的磁滞回线如图2(b)所示。该模型描述STO 忆阻器随时间变化的遗忘效应如图2(c)所示，观察电压为1 mV。

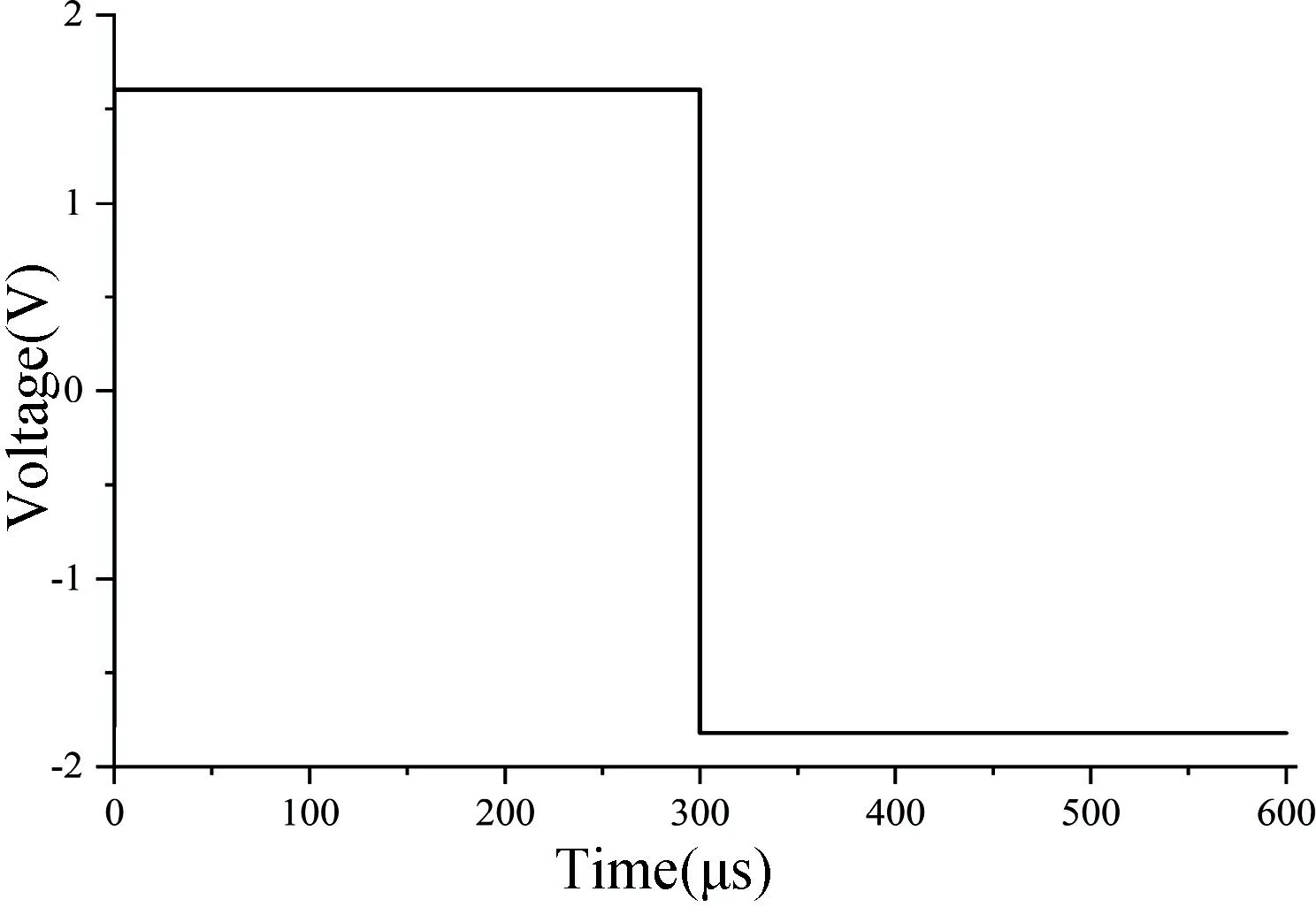
图1 电压激励波形Fig.1 Voltage excitation waveform

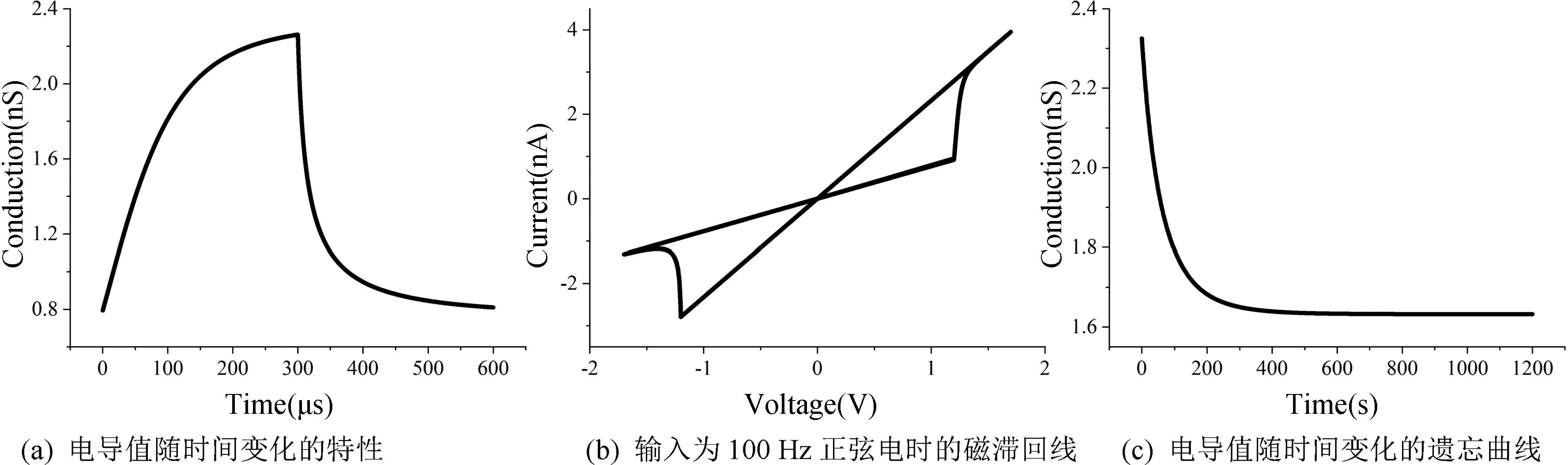
图2 遗忘效应忆阻器的特性Fig.2 The characteristics of the forgetting effect memristor

1.2 激发功能的忆阻器模型

细胞膜的电位变化与其对不同离子的通透性有关，包括K+、Na+和Cl+[26-27]，前神经元和后神经元释放出的尖峰信号可以直接参与突触权重的调节。为了方便研究细胞间的信号传递，一些神经科学的研究者使用简单的数学模型来表达尖峰信号[26]，如式(7)所示。

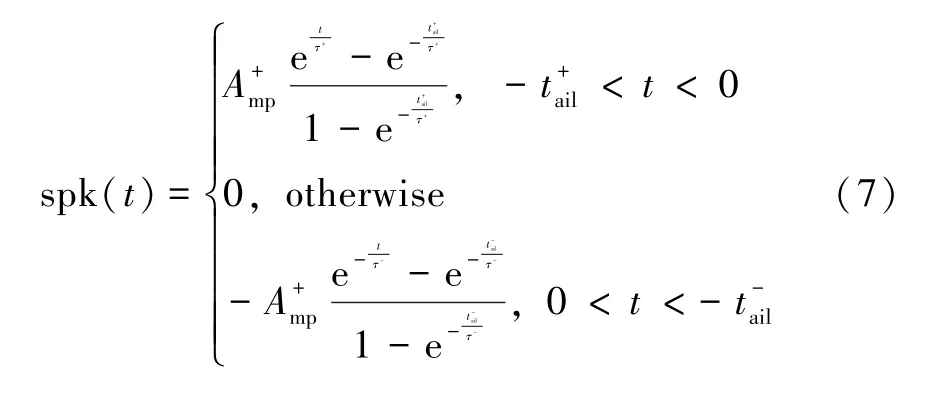
式中:和分别代表尖峰信号的正副幅值;τ+、τ-、和都是时间常数。尖峰信号大致形状如图3 所示。

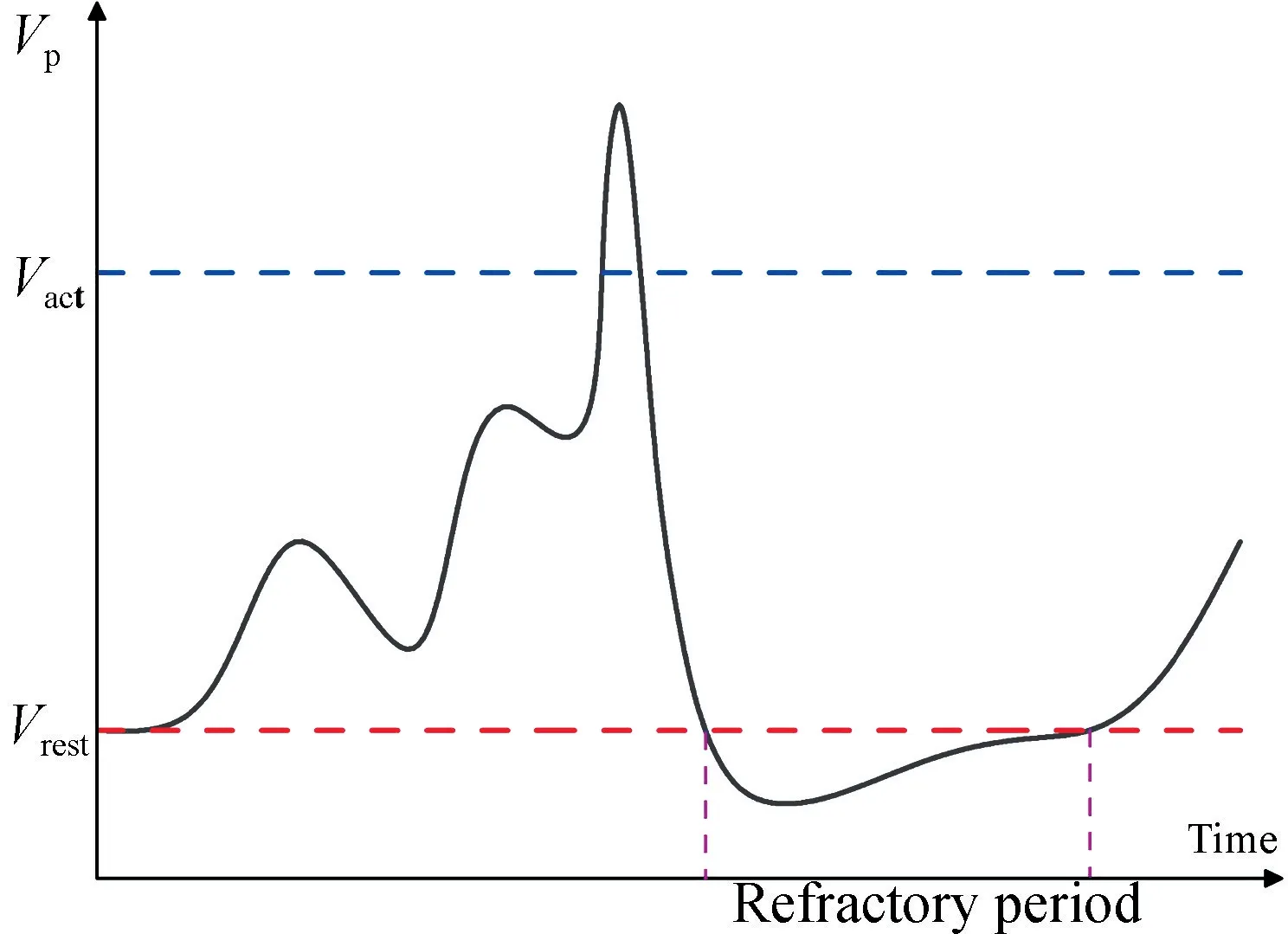
图3 细胞膜电位的变化Fig.3 Changes in cell membrane potential

在脉冲神经元电路中使用压控忆阻器，其阻值也呈指数非线性变化[27]，数学表达式如式(8)所示。θ[V(t)，t]为状态变量，V(t)表示忆阻器两端电压，VTL和VTH为阈值电压，L为隧道势垒宽度，R(t)为忆阻器阻值，其余量为拟合参数。

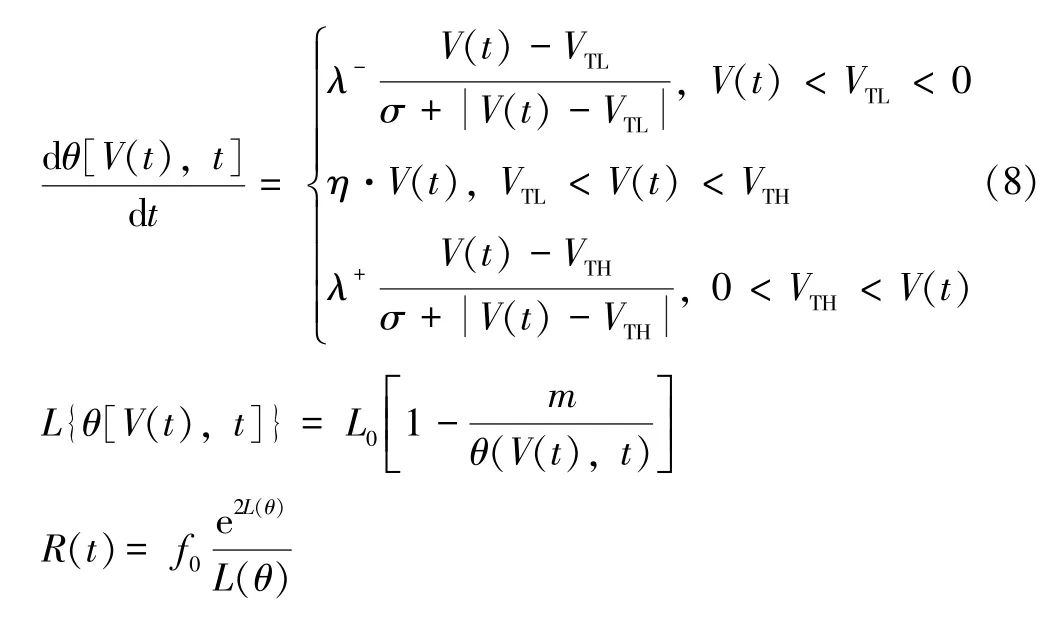
该忆阻器的电流和阻值变化特性如图4 所示，仿真时忆阻器两端施加电压幅值为1.6 V 的脉冲电压，得到忆阻器的阻值变化范围为(2 kΩ，210 kΩ)，阻值在正电压时迅速减小，而在负电压时迅速增大。流经忆阻器的电流与细胞膜电位变化趋势(图1)有一定的相似程度。因此，可以通过对该忆阻器施加脉冲电压的方式得到细胞之间传递信息的尖峰信号。在PSpice仿真中使用以下参数设置:VTH=1.5 V，VTL=-1.5 V，λ+=126×106，λ-=6.2×106，η=0，σ=0.1，m=82，L0=5 nm，f0=310。不同的λ+和λ-会影响阻值变化的快慢，可达到调节电流曲线陡峭程度的作用，将η的值设置为0，可防止当电压低于阈值时阻值发生变化。

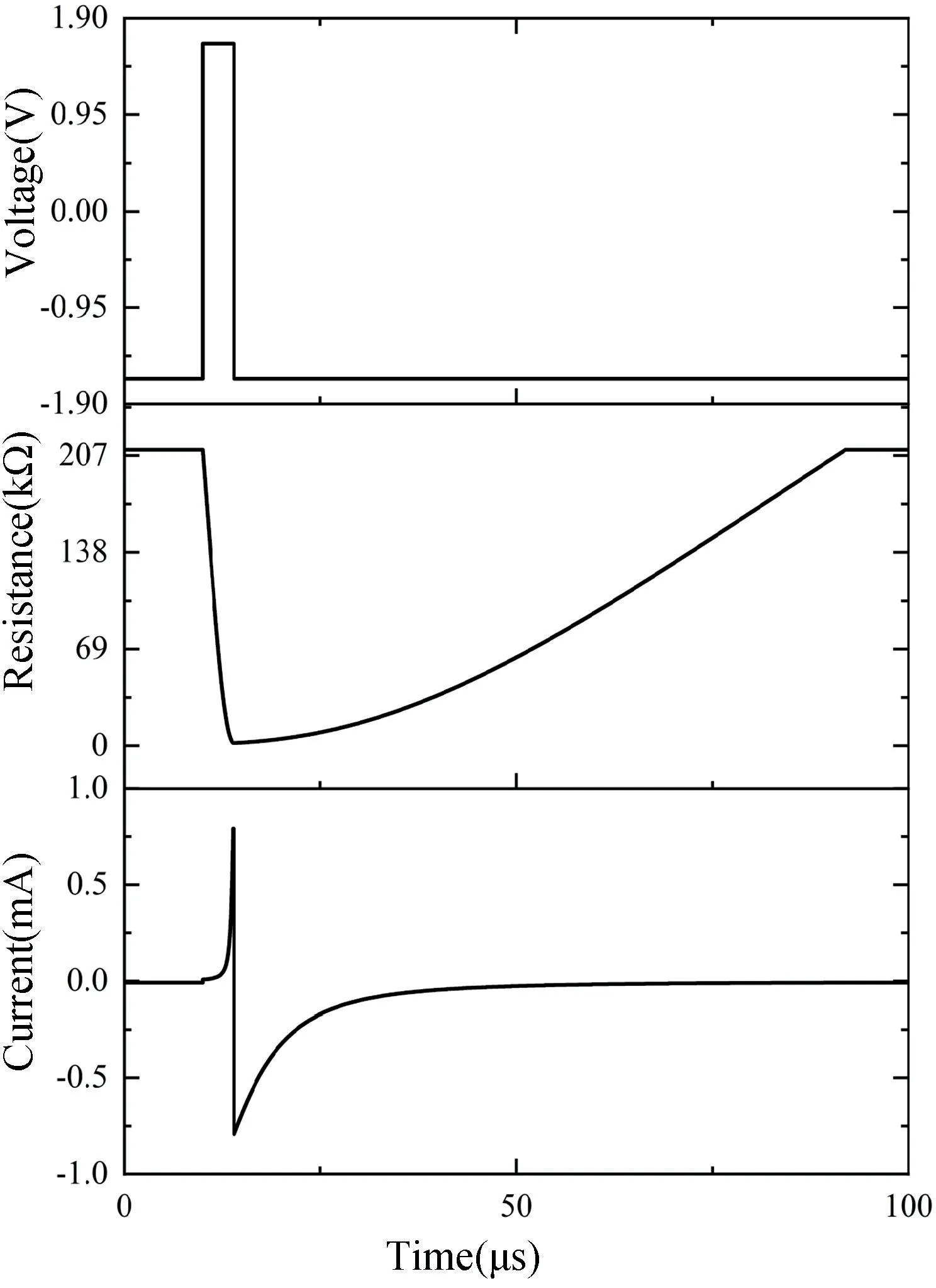
图4 产生尖峰信号的忆阻器特性Fig.4 Memristor properties that produce spike signals

2 神经元电路设计

总体来说，类脑研究方向之一就是以大量人工突触以及神经元相连接组成脉冲神经网络，并以时间编码模式对数据进行分类处理[3]。大脑中最基本的信息处理单元是神经元，它是由树突(输入单元)、胞体(处理单元)和轴突(输出单元)组成[25]。激活的神经元发出尖峰信号，彼此之间通过尖峰数量和时序先后传递信息，与神经元产生的尖峰形状无关。在这一过程中，神经元收到突触前神经元发出的尖峰信号，在时间和空间上对这一信号进行整合，使得该神经元膜电位升高。若在短时间内膜电位并未达到激活阈值电压，则膜电位将缓慢降低，达到短期记忆的特点。在持续刺激神经元使神经元膜电位达到激活阈值电压后，神经元将被激活，产生一个电流尖峰信号，这个信号将通过突触作用到下一神经元[25]。

基于这种原理，本文设计了基于遗忘效应忆阻器的LIF 神经元电路，如图5 所示。一般来说，以电压为神经元输入形式，可简化电路中乘法模块的分布和状态变量到所有神经元突触的电路分布。而输出通常采用电流的形式，这样有利于状态节点的求和操作[28]。

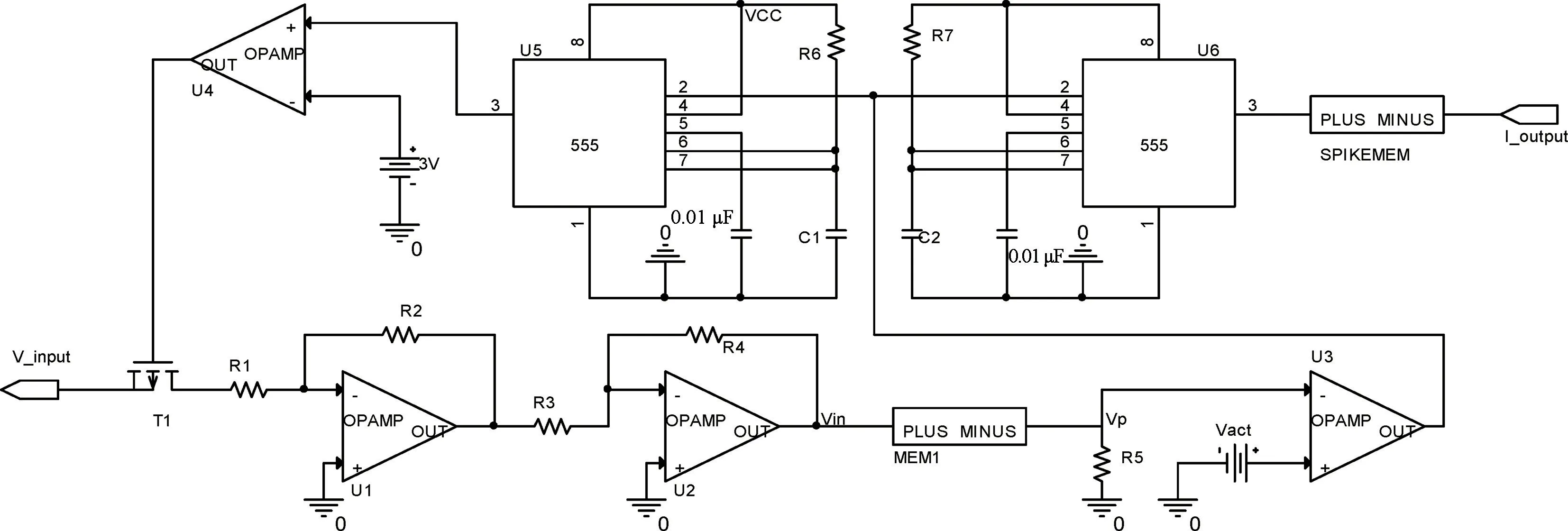
图5 基于遗忘特性忆阻器的LIF 神经元Fig.5 LIF neurons based on the forgetting property memristors

电路描述如下，图5 表示的是一个LIF 神经元电路，T1 是一个P 沟道增强型MOSFET，正常情况下U4 输出低电平(-VCC)，T1 呈导通状态，只有当比较器U4 输出高电平时(+VCC)，T1 才会关断。用输入电压源V_input来表示突触前神经元传递到当前神经元的电压，反相放大器U1 的放大倍数可表示此神经元链接突触前神经元的个数。输入信号经过放大、累加求和(积分求和功能)作用于忆阻器MEM1，使其阻值发生变化，由于MEM1 和R5 的分压作用，膜电位Vp也相应发生变化，如式(9)所示:

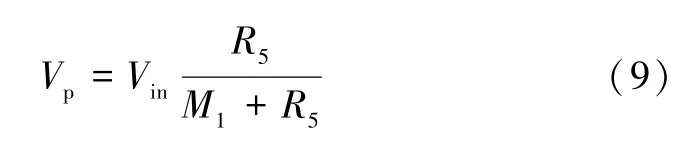
式中:M1为忆阻器MEM1 的阻值;当Vin大于忆阻器阈值电压时，M1逐渐变小，导致电阻R5的分压(Vp)增大。当Vin小于阈值电压时，由于忆阻器MEM1 具有遗忘效应，MEM1 阻值逐渐变大，逐渐恢复到高阻态，使Vp变小，这一过程可模拟神经元的泄漏过程。

当Vp升高到激活阈值电压Vact后，电压比较器U3输出电压由+VCC 突变为-VCC，这一低电平信号使得由555 定时器构成的单稳态触发器U5 触发，发出时间宽度为Tref的高电平脉冲，同时，单稳态触发器U6 发出宽度为4 μs 的脉冲电压，经过忆阻器SPIKEMEM，产生类似于神经尖峰信号的Spike 电流信号(如图3 所示)传递到下一神经元，这可模拟神经元的激活过程。激活信号的前半部分功能主要为刺激突触后神经元膜电位发生变化，后半部分功能主要用来抑制该神经元在短时间内再次激活，以使M1恢复至高阻态，换而言之，使膜电位恢复至静息电位，抑制时间称为不应期。

电阻Rpre表示神经元的突触，突触前神经元的信号经过Rpre传递至神经元，由于神经元输出信号为电流信号，输入信号为电压信号，因此神经元接收到的信号可表示为:

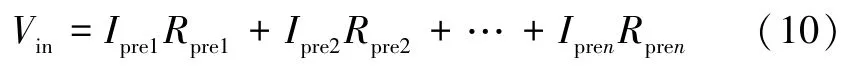
式中:Ipre1，Ipre2，…，Ipren表示突触前神经元发出的信号;Rpre1，Rpre2，…，Rpren可表示神经元之间的权重;因此Vin可表示该神经元在空间上的信息累加，Vin由与之相连的神经元个数和权重共同决定。同时，由于忆阻器MEM1 的遗忘效应，在Vin＜VT+时阻值M1会逐渐增大，因此求和电压Vin的频率也会影响M1的变化，进而影响神经元的激发特性，表现出神经元在时间上的反应。

综上所述，Spike 信号的产生由突触前神经元个数、连接权重以及输入信号的频率共同决定。其中神经元个数和连接权重可模拟空间信号，输入频率可模拟时间信号，因此该神经元电路可表示在时间和空间上的整体反应。

3 LIF 神经元电路的PSpice 仿真

本小节对单个LIF 神经元电路从突触前神经元个数、突触权重以及输入频率3 个方面进行仿真，得到激活特性随输入变化的关系。在仿真中Ipre使用幅值为1 mA、宽度为4 μs 的正脉冲电流来模拟接收到上一神经元的信号，Rpre=1000 Ω 表示输入权重w=1，同时令电路参数为R5=0.4 GΩ，Vact=2.7 V。

3.1 突触前神经元个数n 的影响

如图6 所示，描述了膜电位Vp与突触前神经元个数n的关系，此时假设突触前神经元同时发出相同的信号，同时假设权重w=1，其中黑色虚线代表激活阈值2.7 V。可以很明显地看出当n=10 时，神经元在第2 个信号激活，当n=9 时，神经元在第4 个信号激活，当n=8，n=7 时，神经元将分别在第8、第18 个信号处激活，当n=6 时，神经元不再激活。

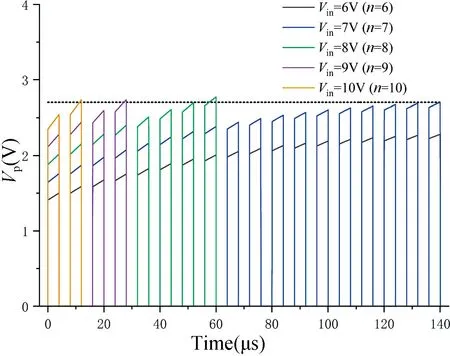
图6 突触前神经元个数n 与膜电位Vp的关系Fig.6 The relationship between the number of presynaptic neurons n and membrane potential Vp

因此得出结论，神经元激活时间随突触前神经元个数的减少呈倍数增加。当n少于最小个数时，神经元将不再激活。

图7 给出了当n=8，w=1 时，LIF 神经元激活的尖峰Spike 信号和膜电位Vp的仿真输出结果。在Spike信号发出期间，神经元膜电位处于静息电位，维持的时间跨度称为不应期。

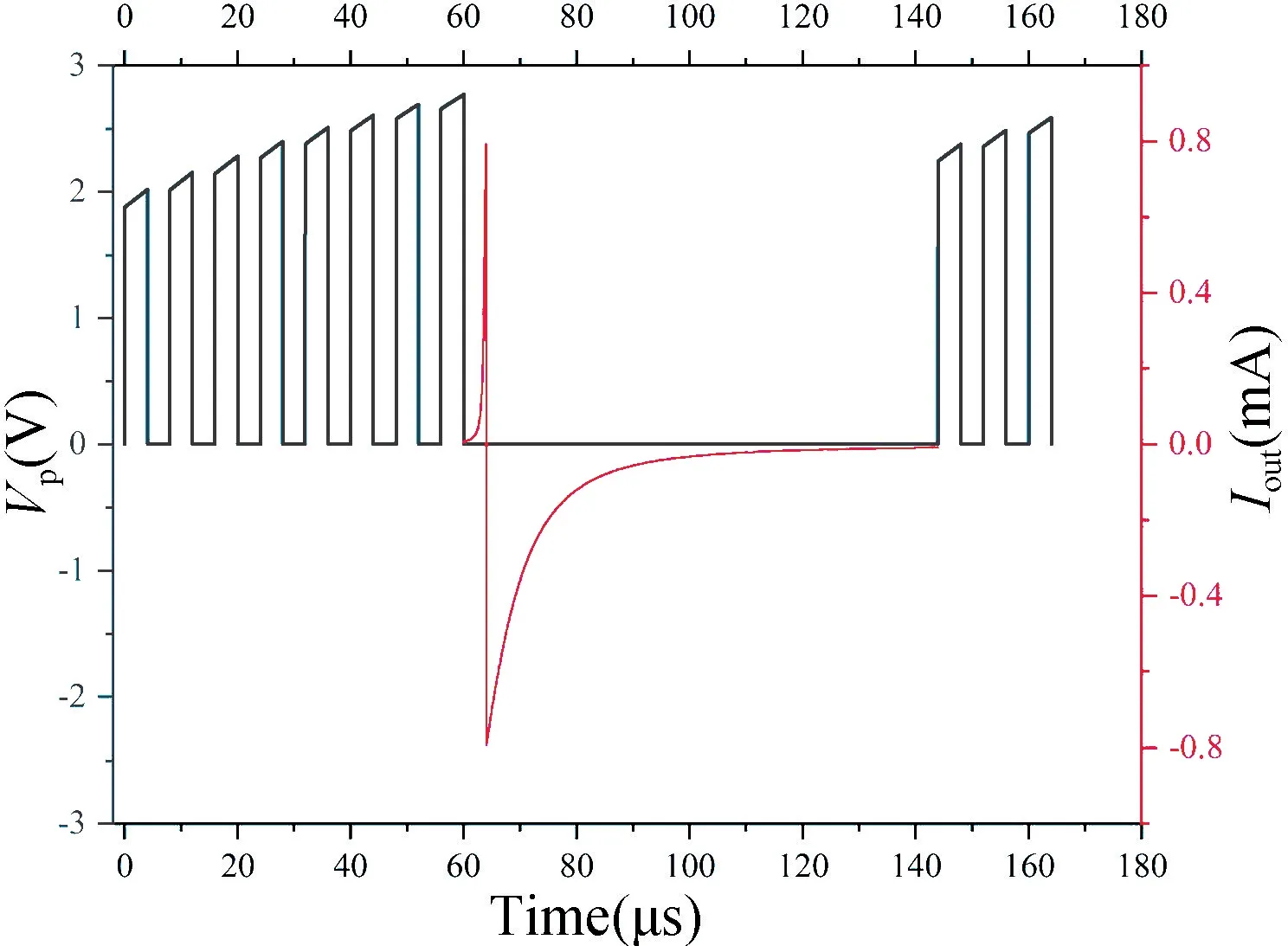
图7 LIF 神经元激活与膜电位Vp的关系Fig.7 The relationship between LIF neuron activation and membrane potential Vp

3.2 连接权重w 的影响

连接权重w对Vp的影响如图8 所示，它与神经元个数n一样，都会影响神经元在空间维度上的激活特性，Rpre=1000 Ω 表示输入权值w=1，即w=Rpre/1000。为体现比较性，假设突触前神经元个数为8 且每个突触权重w都相同。

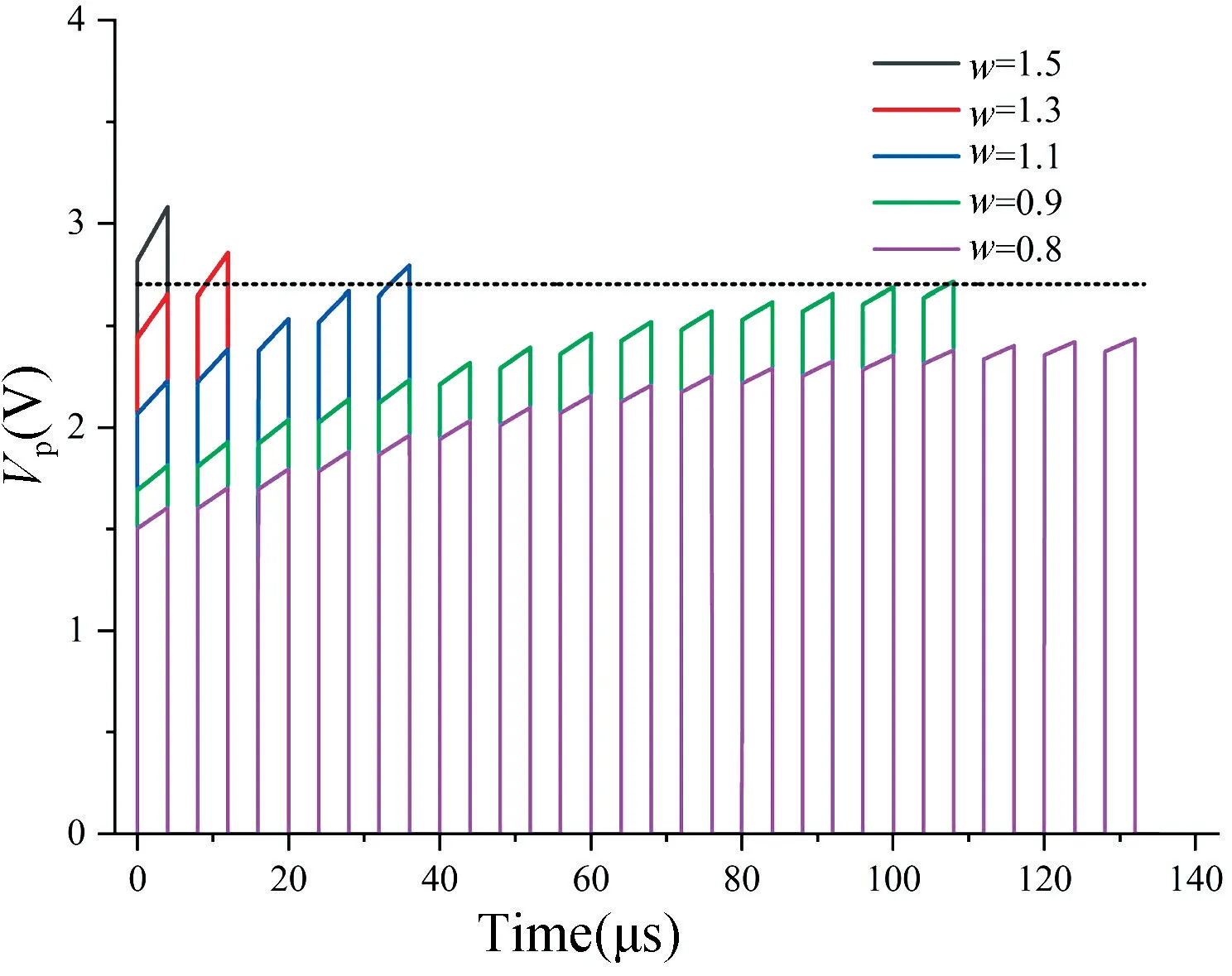
图8 突触权重w 与膜电位Vp的关系Fig.8 The relationship between synaptic weight w and membrane potential Vp

由图8 可明显看出，当突触权重均为w=1.5 时，神经元会在接受第1 个信号时立即激活，在w=1.3，w=1.1 和w=0.9 时，神经元分别在第2，5，14 个信号处激活，当权重均减小为w=0.8 时，神经元不再激活，黑色虚线为激活阈值2.7 V。由此可见，在突触前神经元数量不变的情况下，突触权重越大，神经元接收到的刺激会更强，同时也会更早被激活产生Spike信号。

3.3 输入频率f 的影响

由于忆阻器MEM1 具有遗忘效应，施加大于忆阻器阈值VT+的正向电压，阻值减小，当电压小于阈值时，阻值增大。可见施加电压的频率会直接影响阻值M1的变化，因此输入神经元的频率f会直接影响膜电位Vp的变化。假设突触前神经元个数n=8，突触权重w=1，仿真结果如图9 所示。

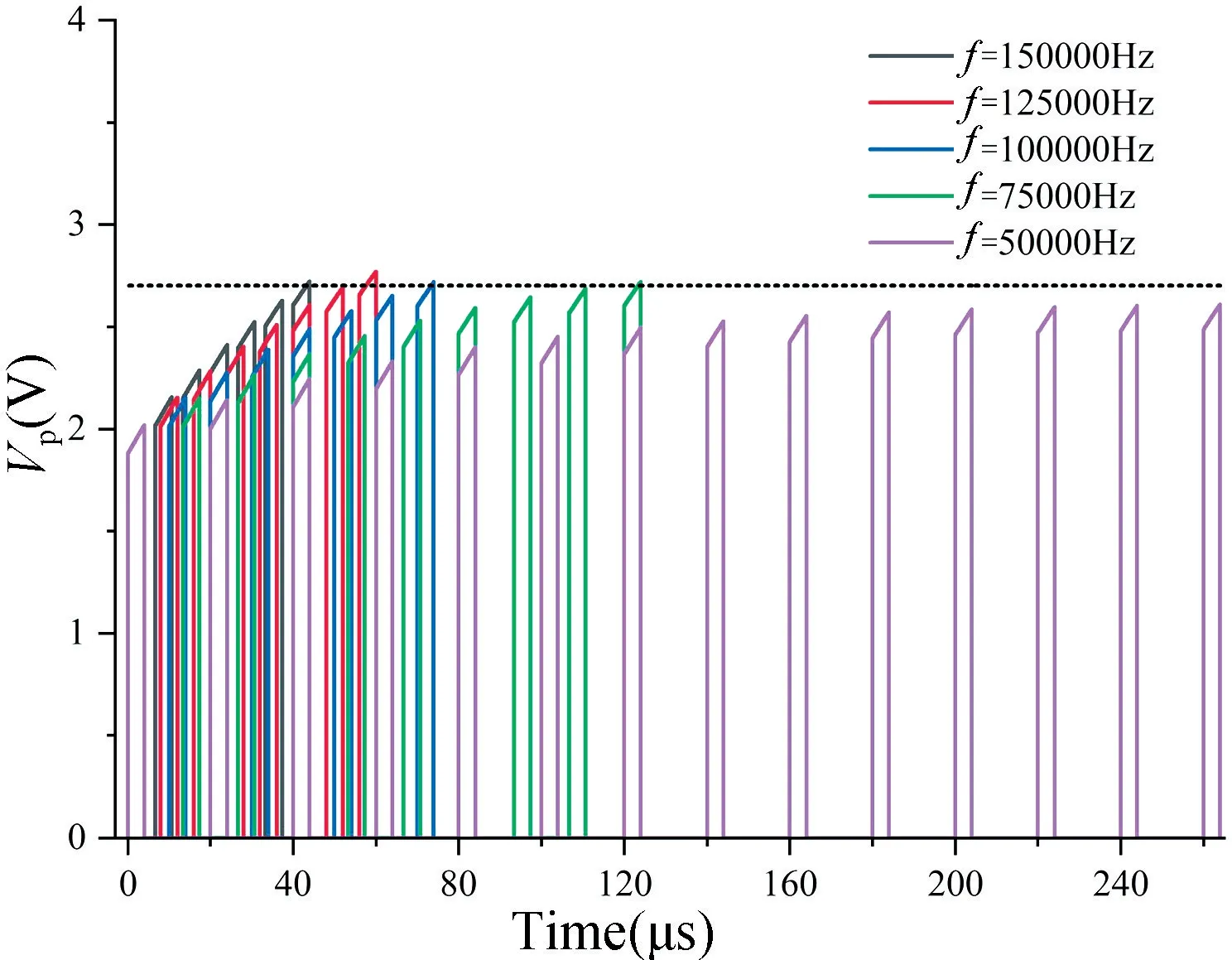
图9 输入频率f 与膜电位Vp的关系Fig.9 The relationship between input frequency f and membrane potential Vp

由图9 可知，当频率f=150000 Hz 时，神经元在43 μs 处激活发出Spike 信号，当频率f=125000 Hz，f=100000 Hz 和f=75000 Hz 时，神经元分别在57，73和123 μs 处激活，而当f=50000 Hz 时，神经元将不再激活。由此可见，要使神经元能正常激活发出Spike信号，在n=8，w=1 的情况下输入信号频率必须大于50000 Hz。

综合上述分析，可以得出LIF 神经元的激活条件由突触前神经元n、突触权重w和输入信号频率f共同决定，其中突触前神经元个数n和突触权重w模拟空间上的累计求和，输入信号频率f可模拟时间上的信息传递，影响LIF 神经元的泄漏过程。突触前神经元个数越多、突触权重越大、输入信号频率越高，神经元会更早激活。LIF 神经元达到激活条件后，由激活信号通过SPIKEMEM 产生Spike 电流信号传递至下一神经元，模拟神经元激活过程。

4 结果与分析

本文基于遗忘效应忆阻器构建了LIF 神经元电路，与M-CNN 神经元结构[29]相比，可多传递时间维度的信息，从而利用Spike 信号进行时间编码，即脉冲时间依赖可塑性(STDP)。

本文构建神经元的不应期为85 μs，表示该神经元的有效积分时间只发生在85 μs 的时间段，是文献[25]不应期时间500 μs 的1/5，计算速度更快。本文中神经元可反映宽度为4 μs 的输入脉冲，与文献[29]中60 μs 的脉冲宽度相比，是其输入频率的10 倍左右，提高了计算速度，在假设单个神经元激活频率与文献[29]相同的情况下，本文所设计的神经元电路可与更多的突触相连接，因此更易构成大规模集成电路。

5 结论

本文首先研究了具有遗忘功能的忆阻器仿真模型，使用PSpice 软件对忆阻值随电压变化、忆阻值随时间变化以及磁滞回线的分析，验证了仿真模型的忆阻特性。结合改进的模型，设计了LIF 神经元电路，在膜电位Vp达到阈值电位Vact时，神经元发出Spike 信号传递至下一神经元，同时使该神经元进入不应期，膜电位保持为静息电位。最后通过分析突触前神经元个数、突触权重以及信号输入频率对膜电位Vp的影响，验证了该电路可实现对时间和空间信息的整体反应。