中速磁悬浮列车的分数阶运行控制方法
张文静,曹博文,李宽欣,高亚苹,岳 强,徐洪泽
(1.北京交通大学 电子信息工程学院, 北京 100044;2.中车唐山机车车辆有限公司,河北 唐山 064000)
磁悬浮列车是一种利用电磁力实现自身悬浮与驱动的新型轨道交通方式,与传统轮轨列车相比具有噪声低、线路适应性强、维护方便以及寿命长等优点[1]。随着长沙磁悬浮快线以及北京S1线的相继开通运营,中速磁悬浮交通有望成为21世纪的主要交通方式之一。
运行控制系统 (Operation Control System,OCS) 是保证中速磁悬浮列车正常运行的中枢系统,是磁悬浮列车运行控制的“大脑”和“神经系统”,主要作用是运行指挥和安全防护。运行控制算法是OCS的核心之一,然而,目前的磁悬浮运行控制系统主要借鉴了传统地铁运用的基于通信的列车运行控制系统 (Communication Based Train Control System,CBTC)系统,尚无成熟的运行控制方法。因此,研究中速磁悬浮列车运行控制算法,研发完全自主知识产权的中速磁悬浮运行控制系统,保障列车运行安全,提高运行效率,具有重要意义。
国内外学者已对传统轮轨列车的运行控制算法进行了深入研究。文献[2]设计出滑模PID组合控制算法,实现列车自动驾驶,提高了列车的运行控制性能。文献[3]结合专家经验与梯度下降算法,设计出一种基于在线调整的自动驾驶算法,提高了列车的位置与速度跟踪精度。文献[4]将无模型自适应控制算法应用于列车运行控制,提高了列车速度控制性能。文献[5]将小波包滤波与迭代学习相结合,降低了各种干扰因素对列车运行控制的影响。文献[6]提出一种加权多模型预测函数,设计出列车运行控制算法,提高了列车动态模型的准确性,实现列车自动驾驶系统的速度与位置跟踪。然而,与传统轮轨列车的牵引方式不同,中速磁悬浮列车的牵引控制位于地面,导致现有的轮轨列车运行控制方法并不完全适用于磁悬浮列车。
目前,对中速磁悬浮交通系统的研究主要集中在悬浮列车控制方面[7-9],尚无有效的列车运行控制算法。中速磁悬浮列车的运行速度较低(≤200 km/h),在曲线或坡道路段受到的线路附加阻力严重影响了列车运行性能,因此对运行控制算法的精度与鲁棒性提出了更高要求。
随着分数阶微积分及分数阶控制理论的发展,分数阶控制算法正在逐渐成为改善控制性能,提高控制精度的重要方法,受到了国内外学者的广泛关注。与传统的整数阶控制算法相比,分数阶控制算法具有控制精度高、系统鲁棒性强等优点[10],得到了广泛的应用[11-14]。
本文以中速磁悬浮列车为研究对象,提出一种基于分数阶PID (Fractional Order PID,FOPID) 的列车运行控制方法。首先,利用粒子群优化-模拟退火算法 (Particle Swarm Optimization-Simulated Annealing,PSO-SA) 辨识列车空气阻力系数,提高中速磁悬浮列车动力学模型的准确性。然后,针对列车目标速度曲线跟踪问题,设计FOPID控制器,通过改进型Oustaloup算法拟合分数阶微积分,利用PSO-SA算法整定FOPID控制器参数。最后,通过与传统的整数阶PID (Integer Order PID,IOPID) 控制算法进行仿真对比,验证了所提出的FOPID控制算法的有效性。
1 中速磁悬浮列车动力学模型
根据牛顿运动定律,中速磁悬浮列车的动力学模型可以描述为
( 1 )

基本阻力Fn始终作用于列车,可以表示为
Fn=Fa+Fe
( 2 )
列车所受空气阻力Fa与车型和线路条件有关[15-16],是列车基本阻力中最大的不确定性因素,单位质量所受的空气阻力可以利用戴维斯方程表示为
Fa=a+bv+cv2
( 3 )
式中:a、b和c为列车空气阻力系数。
Fe为线路两侧的F轨与悬浮电磁铁间的涡流效应产生的涡流阻力,可以表示为
( 4 )
附加阻力Fd仅在特定线路作用于列车,可以表示为
Fd=Fi+Fr
( 5 )
式中:Fi为坡道附加阻力,其大小由列车质量以及坡道坡度决定,可以描述为
Fi=img·sign(φ)
( 6 )
式中:i为坡道坡度的千分数;g为重力加速度;φ为坡道角度,sign(φ)定义为
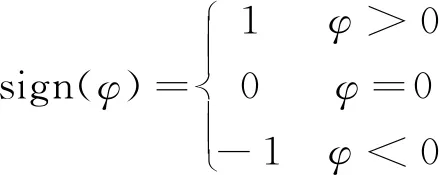
( 7 )
其中,φ>0表示列车处于上坡状态,φ<0表示列车处于下坡状态。
曲线附加阻力Fr可以表示为
(8)
式中:R为弯道曲线半径。
由于空气阻力是中速磁悬浮列车基本阻力中的主要不确定因素,为了降低列车动力学模型中的不确定性,提高模型的准确性,基于PSO-SA优化算法,本文提出了一种空气阻力系数a、b和c的辨识方法。
2 中速磁悬浮列车空气阻力系数辨识
在现有的参数辨识与优化算法中,PSO算法因其实现简单,收敛速度快等优点而得到了广泛应用,但该算法在优化过程中容易陷入局部收敛,难以得到全局最优解。PSO-SA算法在PSO算法的基础上引入SA算法,能够在略微降低收敛速度的情况下,解决局部收敛问题,有效提高参数辨识与优化的精度。
(9)

采集p组数据,则PSO-SA算法的适应度函数可以表示为
(10)

PSO算法中粒子的速度与位置更新规则分别为
vj(t+1)=ωvj(t)+c1r1[pj(t)-xj(t)]+
c2r2[pg(t)-xj(t)]
(11)
xj(t+1)=xj(t)+vj(t+1)
(12)
式中:ω为惯性权重;c1与c2为加速因子;vj(t)为微粒j在第t代的速度;r1与r2为两个服从[0,1]之间均匀分布且相互独立的随机数;pj(t)为微粒j在第t代的个体最优位置;xj(t)为微粒j在第t代的位置;pg(t)为第t代群体最优位置。
利用PSO-SA优化算法,辨识中速磁悬浮列车空气阻力系数,主要步骤如下:
Step1设置迭代次数k、群体规模n,根据PSO算法参数选取策略[17]设置惯性权重ω、加速因子c1及c2,初始化各微粒的速度与位置,根据适应度函数式(10)计算各微粒适应度,确定初始群体最优位置。
Step2执行PSO算法,利用式(11)与式(12)更新各微粒的速度与位置,计算各微粒的适应度,根据适应度更新个体最优位置与群体最优位置;若PSO算法收敛,则执行Step3,否则重复执行Step2。
Step3引入SA算法,设置SA算法初始位置y为PSO算法当前群体最优位置pg(t),设置SA算法的初始温度T、衰减因子h以及Markov链长度s。
Step4在y的邻域内随机选取一新位置y′,分别计算适应度W(y)与W(y′)。
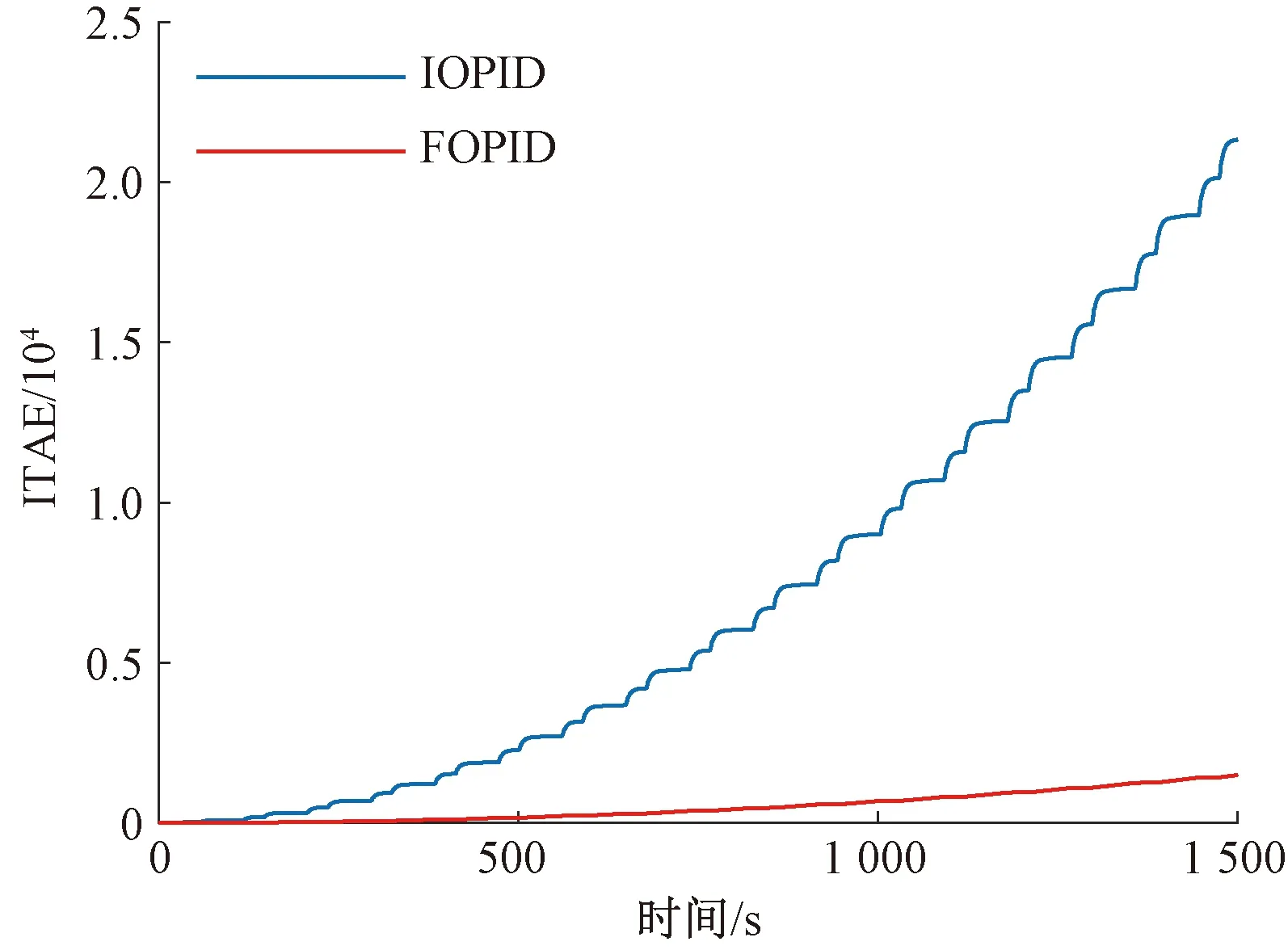
(1)若W(y′) (3)执行退火操作,令T(t+1)=hT(t)。 Step5重复Step4,直至完成s次迭代。 Step6若SA算法最终位置的适应度小于PSO算法的当前群体最优位置pg(t),则将其作为PSO算法新的群体最优位置。 Step7返回并继续执行Step2,直至PSO算法完成k次迭代。 FOPID控制器在传统IOPID控制器的基础上引入了积分阶次与微分阶次,控制输出的取值范围更加灵活,而且对系统参数变化不敏感,具有更高的控制精度和更强的鲁棒性。 分数阶积分定义为 (13) Caputo分数阶微分定义为 (14) 利用分数阶微积分定义,设计FOPID控制器,其传递函数为 (15) 式中:Kp、Ki与Kd分别为比例系数、积分系数和微分系数;λ和μ分别为积分阶次与微分阶次,且0<λ,μ<1。 FOPID控制器的设计主要包括分数阶微积分的拟合以及控制器参数的整定。在现有的拟合算法中,改进型Oustaloup算法[18-19]在拟合频段内对分数阶微积分的幅频特性与相频特性拟合精度高,基于该算法设计改进型Oustaloup滤波器,在拟合频段(ωb,ωh)内的2N+1次滤波器可以表示为 (16) 式中:b,d∈R+;第k个零点、极点和增益分别为 (17) (18) K=(ωbωh)α (19) 由于中速磁悬浮列车运行控制系统具有非线性及不连续性,难以用确定的传递函数进行表征,导致传统频域法整定的FOPID控制器性能较差。针对此问题,本文以运行控制系统的ITAE性能指标作为适应度函数,利用第2节提出的PSO-SA算法整定FOPID控制器参数。其中,ITAE性能指标可以描述为 (20) 式中:t为控制系统的运行时间;e(t)为t时刻系统的运行误差。 本节利用中速磁悬浮列车试验线数据进行仿真研究,线路模型见图1,线路及列车基本参数分别如表1、表2所示。 图1 中速磁悬浮列车试验线线路模型 表1 试验线基本参数 表2 中速磁悬浮列车基本参数 根据实验数据,利用PSO-SA算法辨识中速磁悬浮列车空气阻力系数,PSO-SA算法参数如表3所示,辨识结果得到参数a、b、c数值分别1.46×10-10、1.17×10-10、0.013 2,图2为适应度变化曲线。 图2 空气阻力系数辨识适应度变化曲线 表3 PSO-SA算法参数 FOPID控制器与IOPID控制器的参数整定过程如下: Step1IOPID控制器参数整定。综合考虑控制系统的快速性与平稳性,利用MATLABTM工具箱整定IOPID控制器,得到控制器参数Kp、Ki、Kd的数值分别为1.0×103、1.1×103、1.0。 Step2FOPID控制器参数整定。采用理想阶跃信号作为中速磁悬浮列车速度控制算法的期望输入,利用本文第2节提出的PSO-SA优化算法,以速度误差的ITAE性能指标作为PSO-SA算法的适应度函数,整定控制器参数。PSO-SA算法参数如表4所示,适应度变化曲线见图3,整定后的FOPID控制器参数如表5所示。 表4 PSO-SA算法参数 图3 FOPID控制器参数整定适应度变化曲线 表5 整定后的FOPID控制器参数 设置仿真步长为10-5s,仿真时间为1 500 s。列车单程运行距离为1.58 km,时间为88.5 s,最大加速度为0.9 m/s2,最大速度为97.2 km/h,即27 m/s,单程运行的期望速度-位置曲线见图4。 图4 期望速度-位置曲线 图5给出了期望速度曲线以及FOPID控制器与IOPID控制器的速度跟踪轨迹,图6为FOPID控制器与IOPID控制器的速度跟踪误差,列车在不同线路的最大速度跟踪误差如表6所示。由图5和图6可以看出,FOPID控制下的列车速度跟踪曲线更加平滑,列车运行更平稳,舒适性更好。在平直线路,由于列车运行过程中非线性基本阻力较小,导致FOPID控制器的速度跟踪效果相比IOPID控制器优势不明显;在弯道与坡道线路,FOPID控制器更加有效地降低了较大的线路附加阻力对系统的影响,速度跟踪性能优于IOPID控制器。 图5 FOPID与IOPID速度跟踪轨迹 图6 FOPID与IOPID速度跟踪误差 表6 不同线路段的最大速度跟踪误差 m/s FOPID控制器与IOPID控制器的控制输出曲线见图7,可以看出,相比IOPID控制器,FOPID控制器具有更小的控制输出。 图7 FOPID与IOPID控制输出曲线 为进一步比较FOPID控制器与IOPID控制器的性能,引入列车牵引/制动能耗 (21) 式中:t为列车运行时间。 列车在第8个运行周期内的牵引/制动能耗变化曲线见图8。可以看出,IOPID控制下的列车牵引/制动总能耗为5.31×107kJ,FOPID控制下的列车总能耗为5.25×107kJ,相比IOPID降低了1.1%。 图8 FOPID与IOPID能耗变化曲线 为了验证所提出的FOPID控制算法的有效性,利用ITAE性能指标比较FOPID控制器与IOPID控制器的速度跟踪性能,结果见图9。可以看出,FOPID控制器的ITAE性能指标远小于IOPID控制器,具有更高的速度跟踪精度。 图9 FOPID与IOPID的ITAE性能指标 为了进一步验证本文所提出的FOPID运行控制算法的鲁棒性,在控制参数、试验线基本参数以及中速磁悬浮列车基本参数不变的前提下,加入能量谱密度为108的白噪声。列车在噪声干扰下的速度跟踪轨迹以及速度跟踪误差分别见图10、图11。可以看出,相比无噪声干扰的情况,IOPID控制器在噪声干扰下的控制效果明显下降,而FOPID控制器的速度跟踪性能则下降较小,验证了本文所提出的FOPID运行控制算法的鲁棒性。 图10 噪声干扰下的FOPID与IOPID速度跟踪轨迹 图11 噪声干扰下的FOPID与IOPID速度跟踪误差 针对中速磁悬浮列车运行控制问题,本文考虑磁悬浮列车运行控制系统对控制精度与鲁棒性的高要求,提出一种基于分数阶的运行控制方法。该控制方法主要包含两部分:利用PSO-SA算法辨识列车空气阻力系数,提高列车动力学模型的准确性;在此基础上提出一种满足列车运行控制精度与鲁棒性要求的FOPID控制器,基于改进型Oustaloup算法拟合分数阶微积分,利用PSO-SA算法整定控制器参数,提高控制器性能。仿真结果表明:相比传统的IOPID控制器,本文所提出的FOPID控制器具有更高的控制精度、更强的鲁棒性、更小的控制输出以及更低的能耗,可以在保障中速磁悬浮列车安全运行的同时,降低列车运行能耗。
3 分数阶运行控制器设计

4 仿真验证



4.1 磁悬浮列车空气阻力系数辨识


4.2 控制器参数整定



4.3 仿真分析









5 结束语
——磁悬浮列车稳步发展

