高速铁路斜拉桥钢-混组合箱梁受力及变形性能试验研究

施 洲，余万庆，杨仕力，严爱国，李的平

(1.西南交通大学 土木工程学院，四川 成都 610031；2.中铁第四勘察设计院集团有限公司 桥梁设计研究院，湖北 武汉 430063)

钢-混组合箱梁斜拉桥的跨越能力强[1]，梁高小，相比钢箱梁，组合箱梁具有刚度大，在高速铁路中还具有桥面防腐维护容易，噪声小等显著优势。国外对钢-混凝土组合梁的研究起步较早，欧美国家已制定较系统的钢-混凝土组合结构设计规范[2]。为揭示钢-混组合梁的受力及变形性能，国内外学者[3-8]开展了斜拉桥钢-混组合梁的理论和试验研究。李小珍等[9]针对江津观音岩公路长江大桥钢-混凝土组合梁开展了1∶2模型试验研究，结果表明组合梁承受较大弯矩时，结合面会产生一定滑移，主梁的轴力能够有效抑制滑移趋势。卫星等[10]针对大跨度组合梁斜拉桥的传力机理进行了模型试验研究，结果显示组合梁截面应力基本满足平截面假定，钢主梁以抗弯为主，混凝土板承担较大轴力。Sieffert等[11]研究了铁路列车作用下钢-混组合梁桥跨中横隔板对组合梁受力性能的影响，发现除考虑横向偶然荷载外横隔板的影响很小。Baskar等[12]对钢-混凝土组合梁进行负弯矩和剪力作用下的非线性有限元分析，研究表明非线性有限元模型能够预测组合梁的最不利受力板件和极限承载力，具有良好的精度。钢-混凝土组合结构中，两种材料交界处设置剪力连接件[13]传递因弯矩、偏压受力引起界面处的剪力以保证混凝土桥面板与钢主梁共同受力。Nie等[14]建立组合梁力学模型来研究负弯矩区组合梁的桥面刚度，结果显示负弯矩作用下存在的滑移效应使截面刚度比无滑动时降低10%～20%。侯忠明等[15]对钢-混凝土组合梁桥开展受力性能的理论分析与模型试验研究，给出了考虑桥面刚度折减与简谐荷载作用的组合梁挠度通用表达式。Wang[16]基于均布荷载下简支组合梁挠度解析公式，研究并提出了部分剪力作用下钢-混凝土组合梁最大挠度的算法。

目前，相关钢-混组合梁斜拉桥的应用与研究主要集中于公路，应用于高速铁路斜拉桥鲜有研究。鉴于高速铁路桥梁活载大、轨道位置固定、变形要求高等特点，依托国内首座高速铁路钢-混组合箱梁斜拉桥——赣江特大桥开展组合箱梁仿真分析及全截面缩尺模型试验，深入研究其受力与桥面变形性能。

1 高速铁路钢-混组合箱梁构造特点

昌吉赣高速铁路赣江特大桥主桥采用(35+40+60+300+60+40+35) m混合梁双塔斜拉桥跨越赣江，设计速度为350 km/h。主梁由中跨的钢-混组合箱梁及两侧混凝土箱梁组成。桥面宽16.3 m，梁高4.475 m，桥面上铺设无砟轨道板。钢梁为两侧带风嘴的开口单箱三室结构，在纵向每12 m设置一道连接混凝土板的横隔板，12 m节间内中部设一道横隔板及其两侧3 m处各设一横肋。预制混凝土桥面板在横向分为3块，两侧边板宽4.15 m，中板宽4.1 m，纵向跨度12 m，标准厚度30 cm，在钢梁上翼缘及横隔板附近区域加厚至50 cm。预制桥面板通过湿接缝与开口钢箱梁上翼缘及横隔板四边连接，湿接缝内设置连接钢筋及剪力钉，剪力钉采用φ22，高15 cm的圆柱头焊钉，其材料为ML15。组合梁横截面见图1。

图1 钢-混组合箱梁截面(单位：mm)

对比既有桥的组合梁结构形式，该桥组合梁构造有如下特点：①首次将钢-混组合箱梁用于大跨度高速铁路斜拉桥，采用单箱三室的开口钢箱梁，通过湿接缝与剪力钉连接混凝土预制板；②预制混凝土桥面板纵向12 m的大节间布置，显著大于公路桥梁组合箱梁桥混凝土板在纵桥向4～6 m的常规跨度；③首次在速度350 km/h高速铁路斜拉桥组合箱梁上铺设无砟轨道板，对桥梁在施工至运营阶段的整体变形、局部变形等提出更高的要求。因此，组合箱梁的受力传力特性、桥面刚度问题值得深入研究。

2 钢-混组合箱梁受力与变形特性分析

2.1 钢-混组合箱梁有限元模型

为系统研究高速铁路斜拉桥钢-混组合箱梁的受力与变形特性，采用Ansys软件建立赣江特大桥钢-混组合箱梁节段有限元模型并开展计算分析。根据结构对称性，考虑圣维南原理，建立半幅桥宽、3个标准梁段长36 m的组合箱梁的有限元模型，并在对称面釆用正对称约束，见图2。模型中采用板单元(Shell63)模拟钢结构、实体单元(Solid45)模拟混凝土桥面、梁单元(Beam44)模拟剪力钉、杆系单元(Link8)模拟桥面预应力钢筋。该3节段混合单元有限元模型共包含108 179个节点，124 522个板单元，469 247个实体单元，7 898个梁单元。模型靠近桥塔端采用固定约束，远离桥塔端为自由端。钢-混结合面处钢板与混凝土桥面板单元采用节点三向平动自由度耦合连接；剪力钉与混凝土单元同样采用节点三向平动自由度耦合连接。

图2 组合梁几何模型

2.2 钢-混组合箱梁应力分布特性分析

原桥梁段在“主力+附加力”组合中最大正弯矩、最大负弯矩、最大轴力3种工况下的有限元仿真分析结果表明，组合箱梁整体受压，最大负弯矩工况受力最为不利。其中最大负弯矩工况下主要构件受力见表1。三种工况下中腹板中部正应力沿梁高分布见图3。

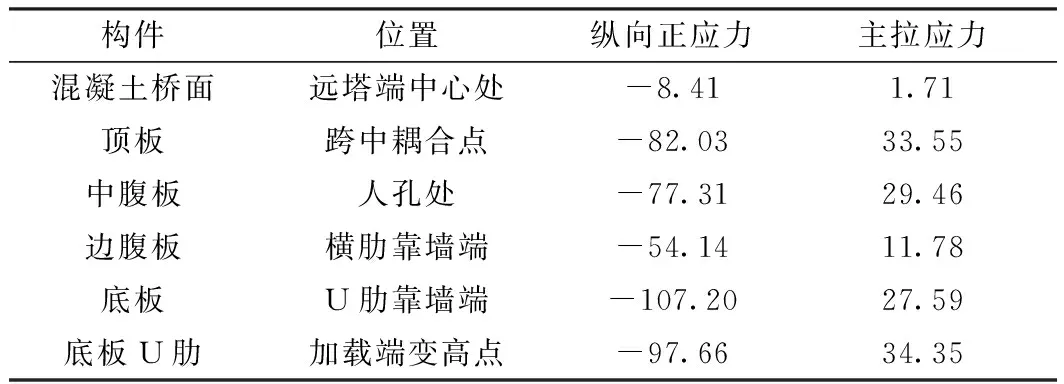
表1 最大负弯矩工况下各板件最不利正应力 MPa

图3 中腹板应力沿梁高分布

由表1可知，钢梁纵向正应力基本在-100 MPa以内，最大为-107.2 MPa，出现在底板U肋靠墙端。混凝土桥面板纵向正应力总体在-7.0 MPa以内，最大值为-8.41 MPa，出现在远塔端的桥面中心线处。箱梁部分构件如剪力钉连接处等存在一定应力集中，并存在局部的主拉应力，但其量值并不显著。钢箱梁的顶、底板应力值较高，为受力关键区域，腹板靠近顶板与底板区域应力值亦相对较高，腹板加劲肋与底板U肋的设置，有效减小了板件的应力量值。由图3可知，在3种工况下，中腹板纵向正应力量值介于-77.23～0 MPa之间，以受压为主；由于构造特性与刚度差异，中腹板纵向正应力沿梁高并不呈线性分布，与顶底板连接部位受力较为复杂。

2.3 钢-混组合箱梁桥面变形特性分析

大桥成桥后铺设无砟轨道板，此时桥梁恒载变形已完成，因此施工过程中对主梁线形要求严格。列车活载下桥面变形包括主梁整体变形和节间局部变形，分别可导致轨道长波、短波不平顺。主梁整体变形在设计时基于全桥有限元分析控制列车活载下挠跨比以满足无砟轨道线路要求。为进一步分析高速铁路列车行车下桥面局部变形特性，计算原桥梁段混凝土桥面板在列车轮轴荷载下桥面局部挠度结果，并计算梁段节间纵、横向挠跨比。挠度计算结果表明：列车轮轴荷载下，梁段节间纵向及横向挠曲变形呈近似正弦波分布，沿桥面中心线的节间相对挠度值最大为3.95 mm，横桥向节间相对挠度值最大为3.86 mm。列车轮轴荷载下梁段局部纵桥向挠跨比为1/3 038，局部横桥向挠跨比为1/2 112，桥面纵向与横向局部挠跨比均较小，表明在高速列车荷载作用下桥面局部具有良好的刚度。

3 高速铁路钢-混组合箱梁模型试验

3.1 模型设计

为进一步研究高速铁路斜拉桥钢-混组合箱梁的受力与变形性能，根据赣江特大桥原桥标准梁段结构构造，开展模型试验研究。基于应力等效原则按照1∶3缩尺比例设计并制作组合箱梁全截面试验模型，通过调整试验模型加载力及施加方式使得模型考察区域的应力及其分布规律同原桥基本相同。试验模型一端顶紧反力墙，另一端作为加载端。加载时采用多个加载千斤顶、分载梁及锚固于反力墙的钢绞线组成的自平衡加载系统进行加载。各板件高度、厚度、长度、板件间距等均按缩尺比设计，部分板件在保证模型截面面积、惯性矩不变的原则下进行调整。模型中剪力钉、普通钢筋及预应力筋均按面积等效设计。对试验模型的混凝土板采用张拉无黏结预应力钢筋来模拟全桥预应力钢筋。为试验加载等效、方便，并防止加载点局部屈曲，在试验模型上设计了反力墙端局部加劲肋、加载端T形肋及加载面板等构造。模型结构设计中根据有限元试算调整。最终试验模型总长度8.46 m(含加载端构造长度)，宽5.43 m，高1.49 m。模型钢结构板件采用同原桥相同的Q345qD钢材料，混凝土采用与原桥一致的C55微膨胀型混凝土，剪力钉材质采用ML15，普通钢筋为HRB335。模型总体布置见图4。

图4 模型及加载布置(单位：mm)

为验证试验模型的等效性，根据最终试验模型的有限元模型，计算最大正弯矩、最大轴力、最大负弯矩等效加载工况下的应力结果，并与原桥应力对比分析等效情况，结果表明，钢-混组合箱梁试验模型各主要受力板件关键测点的应力等效性良好。与原桥相比，模型钢结构主要测点应力绝对误差基本在3.5 MPa以内，相对误差值在5%以内。除极少部分点的模型应力比原桥应力小外，其余模型测点的应力均相比原桥应力接近或略大，钢-混组合箱梁关键构造处应力情况得到良好模拟。

3.2 加载与测试

模型试验主要考察受力最为不利的最大轴力Nmax工况、最大负弯矩Mmin工况下赣江特大桥钢-混组合箱梁节段受力与变形特点。此外，在最大正弯矩工况下叠加一个竖向ZK列车荷载作用Pi工况，考察双线列车荷载作用下混凝土桥面板的刚度状况。模型试验中，各加载工况下的加载荷载值根据赣江桥全桥分析结果等效确定，见表2。试验模型的轴力通过布置于模型加载端与加载梁之间的千斤顶进行加载；模型弯矩通过轴力偏心来实现；剪力及竖向ZK列车荷载通过锚固于地板的竖向预应力钢束配合千斤顶加载。加载端面共布置8个千斤顶，顶部共布置4个千斤顶，见图4。为考察组合箱梁实际受力性能，在试验加载中，最大轴力、最大负弯矩工况分别加载至1.6、1.3倍，单个千斤顶的最大加载力为3 872.5 kN，千斤顶总加载力最大达到21 710.6 kN。各试验加载工况中，为保证测试数据的稳定性，在各级荷载作用下保持2 min，再进行应变与挠度数据采集。

表2 实际内力与等效内力

试验测试包括应变和几何变形测试。根据结构受力特点及有限元计算结果，试验的应力测点布置以混凝土板、钢顶底板、钢腹板、U肋及剪力钉等主要受力构件为主，兼顾各类隔板，合理布置应变片与应变花，全模型共布置631个测点，其中319个单片，104个应变花。为测试钢-混组合箱梁的几何变形状况，了解其在双线ZK荷载作用下的桥面刚度，布置挠度测点20个，其中顶板10个、底板含支座处10个测点。模型的挠度测点、剪力钉测点及部分关键应力测点布置见图5。图5中字母“T”“B”+数字的编号分别代表顶面和底面挠度测点；“C”“S”+数字及仅数字分别代表混凝土、剪力钉和钢的应力测点。

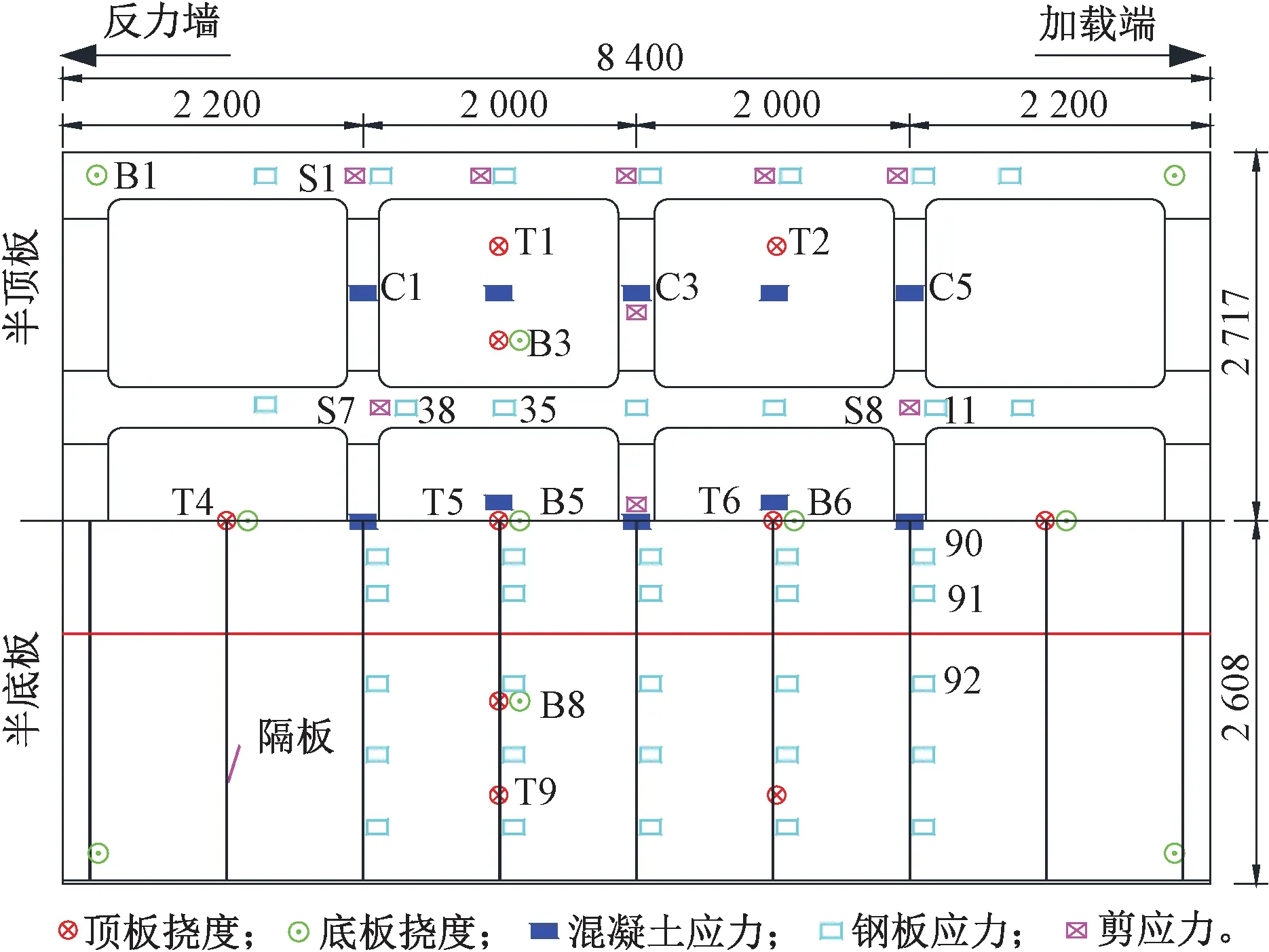
图5 顶板、底板挠度及部分关键应力测点(单位：mm)

4 高速铁路钢-混组合箱梁受力特性

4.1 应力试验结果与分析

由应力实测结果可知：在最大负弯矩工况及最大轴力工况作用下，组合箱梁均以受压为主，纵桥向受力较为均匀，实测应力结果与理论计算值相符良好。1.0倍工况作用下，桥面板混凝土均处于受压状态，其中，最大压应力出现在C5测点，值为-9.91 MPa。钢结构各应力测点应力最大为-124.82 MPa。1.3～1.6倍超载工况作用下，混凝土部分最大压应力为-18.17 MPa，钢结构各测点应力最大为-203.23 MPa。结构测点应力随着荷载的增加近似呈线性增长趋势，混凝土和钢结构部分均在弹性状态下工作，承载能力有一定余量。剪力钉弯曲应力介于4.19～-16.29 MPa，其量值相对较小，并随荷载增加呈现线性增长，表明钢-混连接部处于弹性工作范围，未出现钢-混黏结滑移、脱空等非线性受力情况。其中最大负弯矩工况下混凝土桥面、钢梁及剪力钉部分实测的荷载-应力曲线见图6、图7。

图6 混凝土桥面板荷载-应力曲线

图7 钢主梁荷载-应力曲线

最大负弯矩工况作用下，试验模型中腹板处钢梁截面沿梁高度方向测点应力的分布状况见图8。由图8可见,分级荷载作用下测试应力与理论计算应力沿梁高的分布规律基本一致，组合箱梁应力沿梁高呈非线性分布。

图8 纵桥向应力沿中腹板高度分布

4.2 组合箱梁传力机理分析

为进一步研究钢-混组合箱梁结构的传力特点，基于试验实测应力结果来研究其传力机理，引入组合箱梁结构板件荷载分配百分比Pi，并在此基础上定义钢主梁各板件的受力不均匀程度系数Cj，即

(1)

(2)

(3)

式中：P1，…，Pi，…，Pn为钢主梁部分各构件承担的荷载比例；Pn+1为混凝土桥面板所承担的荷载比例；n为钢主梁全部板件数(包括顶板，斜底板，平底板，U肋，中腹板，边腹板及加劲肋)；j为考察的主梁截面号；ti为钢主梁各板件厚度；li为钢主梁各板件长度；ri(l)为钢主梁各板件在截面处的纵向正应力。

最大负弯矩工况下模型中部节间各关键截面混凝土和钢主梁各板件的荷载分配比例及受力不均匀程度系数见表3、图9。其中Z=0～4 m为模型中部一个标准节段的长度。

表3 各构件内力传力比例理论值

图9 结构内力分配

由表3及图9(a)可见：钢主梁与混凝土桥面板沿纵桥向各关键截面轴力分配比例变化平缓无突变。在Z=0～4.0 m节段内，钢主梁承担的轴力从35.35%增加至52.26%，混凝土桥面板承担的轴力从64.65%减小至47.74%，该变化表明组合箱梁从近塔侧到远塔侧轴力逐渐由混凝土桥面板向钢主梁传递。钢主梁各板件受力不均匀程度系数C的在1.92～2.78的范围内波动，最大值为2.78，表明各板件受力不均匀明显。

由图9(b)可见：斜底板承担的最大轴力比例为16.63%，平底板承担的最大轴力比例为8.89%，前者的轴力分配比例约为后者的两倍。在Z=0～4.0 m节段的各关键截面，中腹板与边腹板承担的轴力由近塔侧到远塔侧线性增大，混凝土桥面板由近塔侧到远塔侧线性减小的轴力主要由腹板及钢顶板承担。组合箱梁的U肋及加劲肋承担的轴力较小，承力比例最大为2.01%，在传力过程中的作用较小，其主要作用在于防止板件局部失稳。

针对关键的Z=0、2.0、4.0 m截面，采用试验实测数据计算构件承担荷载比例并与有限元结果进行验证，结果见表4。由表4可见，试验实测结果与有限元计算结果得到的构件荷载承担比例相近，最大差值不超过5%，有限元分析与模型试验的结合能够较精确的分析钢-混组合箱梁的传力机理。

表4 结构承担荷载比例P

5 高速铁路钢-混组合箱梁桥面刚度

5.1 桥面变形测试结果与分析

在无桥面竖向荷载的2种工况下，混凝土桥面板最大挠度为0.16 mm，出现在两节段跨中，箱梁节段桥面挠度很小。在最大正弯矩工况中再叠加1.0倍双线ZK列车荷载工况下，混凝土桥面板最大挠度为1.52 mm。当双线ZK列车荷载增加至1.6倍时，桥面板最大挠度为2.09 mm，但仍小于TB 10621—2014《高速铁路设计规范》[17]规定的容许值2.5 mm。桥面节间挠度在纵桥向呈现半正弦波变形分布，在横桥向因双腹板的构造而呈现一个半正弦波分布。最大负弯矩工况及ZK列车荷载工况作用下顶板中心线挠度测点T4、T5与底板中心线挠度测点B5、B6的荷载-位移曲线见图10、图11，其中“单”“双”分别代表单、双线列车荷载等级，即试验中为对比单、双线加载的差异而保持主梁1.0倍最大正弯矩加载并将竖向单、双线荷载交替增量加载。

图10 最大负弯矩工况挠度

图11 最大正弯矩+列车荷载工况挠度

由图10可见，最大负弯矩加载工况下桥面变形呈现线性变化，在无竖向荷载下主梁竖向变形量最大为0.16 mm，量值极小。由图11可见，在最大正弯矩工况下，主梁竖向变形量最大为0.69 mm；主梁在竖向ZK荷载作用下，单线1.0倍加载及双线交替增加至1.6倍时，主梁挠度最大增量为1.39 mm，主梁两侧高差均小于0.5 mm，按照相似比对应原桥为1.5 mm，参考高速铁路轨道静态铺设精度标准2 mm/5 m(3 m)的高低(扭曲)可见，偏载对箱梁的竖向变形影响较小，其原因在于单箱三室截面的主梁具有良好的抗扭刚度。

5.2 组合箱梁桥面挠度拟合分析

桥面板短波不平顺性对速度350 km/h的高速列车的行车安全性影响显著，为分析组合箱梁段在双线ZK列车荷载作用下的桥面变形规律，基于板壳结构受力变形解析理论，采用有限元分析与试验实测数据相结合的方法，对有限元模型混凝土桥面板设定横向及纵向路径并计算得到模型横向及纵向单跨挠度Uz值，对有限元计算结果及实测结果进行公式拟合修正，得到组合箱梁桥面竖向挠度在横桥向、纵向的分布波形公式为

(4)

(5)

式中：Uz1，Uz2分别为挠度在横桥向、纵桥向的分布，mm，以向下为正，挠度横向分布扣除了截面整体下挠，纵向分布扣除了整体的变形；y、x分别为距混凝土桥面板横桥向、纵桥向自湿接缝支撑点起的跨度距离，mm；q为单线列车荷载集度，N/mm；B、L分别为单块预制混凝土桥面板横向与纵向长度，mm。

桥面变形的拟合公式结果及其与有限元计算值、实测值的对比见图12。

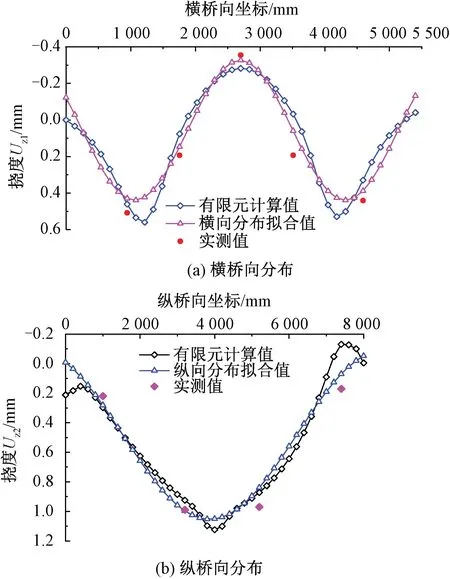
图12 挠度纵向和横向分布

由图12可知，有限元计算挠度与试验实测值相符良好。桥面变形拟合公式结果与有限元计算值及实测值总体相符良好，在端部及约束处，因变形量值小导致误差相对较大；其余区域拟合公式与有限元结果的正负误差均在10%以内；拟合公式与实测数据的误差基本在15%以内，有效反映双线ZK列车荷载作用下桥面的挠度变化情况，可为类似桥面挠度分析提供参考。

5.3 组合箱梁桥面变形挠跨比分析

为研究组合箱梁标准节段在ZK列车荷载作用下的桥面刚度特点，对比分析了局部纵、横向挠跨比的理论计算结果与试验结果，见表5。

表5 试验模型挠跨比理论值与实测值对比

由表5可知，纵桥向挠跨比为1/2 631，横桥向挠跨比为1/2 123，略小于原桥纵、横向挠跨比理论值1/3 038、1/2 112，均小于规范[17]限值1/1 600。挠度在标准梁段跨中达到最大，沿两侧逐渐减小，总体分布趋势与理论计算相近。纵桥向挠跨比稍小于横桥向挠跨比，表明桥面板纵桥向刚度稍强于横桥向刚度。

6 结论

(1)高速铁路斜拉钢-混组合箱梁在3种最不利荷载组合工况下，混凝土桥面板最大压应力为8.36 MPa，钢主梁最大压应力为100.01 MPa，其余多在80 MPa以内，钢主梁顶板、底板应力值较高，为受力关键区域。大多数测点应力实测值与原桥模型计算值相符良好。荷载加载至1.6倍，钢和混凝土间未发生滑移，各测点荷载-应变(位移)基本呈线性关系；表明钢-混组合箱梁受力性能良好。

(2)钢主梁与混凝土桥面板沿纵桥向轴力传递比例呈线性变化；钢主梁传递轴力由35.35%增加至52.26%，钢主梁各板件受力不均匀程度系数C在1.92～2.78的范围内波动，表明各板件受力不均匀明显；混凝土桥面板传递轴力由64.65%降小至47.74%。

(3)竖向单线1.0倍ZK荷载加载及双线交替增加至1.6倍时，主梁挠度最大增量为1.39 mm，主梁两侧高差均小于0.5 mm，小于轨道2 mm/5 m(3 m)的高低(扭曲)精度要求，表明偏载对箱梁的竖向变形影响较小。

(4)在双线ZK荷载工况作用下，模型桥面纵、横向挠度呈现较平顺的正弦波分布，混凝土板竖向位移最大值为1.52 mm，纵桥向挠跨比为1/2 631，稍小于横桥向挠跨比1/2 123，均小于规范限值1/1 600，表明组合箱梁桥面板具有良好的刚度。