考虑管状导体模型和轨中电流的钢轨电位计算

刘 炜，李思文，杨 龙，樊国桢，潘卫国

(1.西南交通大学 电气工程学院，四川 成都 610031; 2. 北京全路通信信号研究设计院集团有限公司, 北京 100071)

直流牵引供电系统中，钢轨是主要的回流传输路径，近些年来钢轨电位问题日趋严重。为了防止钢轨电位过高对人身造成的危害，在各个车站及停车场安装钢轨电位限制器(Overvoltage Protection Device,OVPD)[1]。目前国内地铁线路运营时钢轨电位经常达到120 V甚至更高，OVPD频繁动作后闭锁接地情况屡屡发生。

直流牵引供电系统中，钢轨电流的频率成分主要来源于两部分：①直流牵引变电所整流带来的特征谐波和非特征谐波[2-3]，采用24 脉波整流后，这部分分量含量不大；②地铁车辆逆变器输出VVVF 交流电压给交流牵引电机时，在逆变器的输入侧产生6倍频的谐波电流成份。

图 1为某地铁OVPD动作前钢轨电位波形，钢轨电位频谱中交流分量为12.16 V，直流分量为137.183 V；6倍频成分占总交流分量的75.8%。

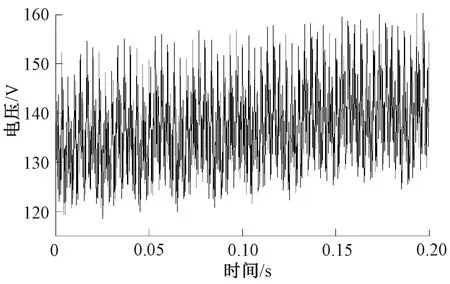
图1 动作前钢轨电位波形

轨中电流交流频谱和钢轨电气参数对钢轨电位计算有很大影响[4]。文献[5]利用Bessel函数给出了管状圆柱导体内阻抗计算公式。该公式在圆柱导体上得到了很好的应用，但是钢轨为工字形截面无法用该公式计算。文献[6]指出钢轨等效为管状圆柱导体模型是针对不规则导体计算阻抗的常用模型且精度较高，但是在计算过程中难以确定管状导体参数的数值，并且随着频率的增大，Bessel函数级数展开式逐渐不可靠。

文献[7-9]提出使用标记法和多项式近似Bessel函数，解决了大参数的问题却忽略了Kelvin函数的影响且未给出钢轨等效管状圆柱导体计算参数。文献[10-11]结合有限元建模仿真FEM提出管状圆柱导体4个参数数值计算方法，但是有限元仿真结果的准确性有待考证。

针对现有钢轨交流内阻抗测量困难[12]且计算模型参数较多而复杂的问题，本文在实验室搭建钢轨交流内阻抗实验平台，实测不同频率下的钢轨阻抗数据拟合确定P60钢轨管状模型参数；对直流牵引供电结构进行解耦，建立钢轨-地分布式参数模型，提出考虑轨中电流交流频谱下的钢轨电位计算公式。通过实验室和工程案例验证了方法的准确性。钢轨电位的准确计算对分析城市轨道供电屡屡发生的异常钢轨电位问题(尤其是OVPDII段动作)、抑制钢轨电位措施的研究有着重要的意义。

1 钢轨管状导体模型

1.1 管状导体模型原理

在交流电流激励下，由于导体的铁磁特性，电流不均匀地分布在导体截面，这导致导体在不同频率下的内阻抗存在差异。当只考虑集肤效应，忽略邻近效应、温度带来的影响时，管状导体的内阻抗为

( 1 )

( 2 )

( 3 )

ω=2πf

( 4 )

式中：re为导体外径；ri为导体内径；σ为导体电导率；f为电流频率；μ为导体磁导率，μ=μrμ0。其中，μr为相对磁导率，μ0为真空磁导率；ber()、bei()为Bessel函数；ker()、kei()为Kelvin函数。

但是钢轨作为“工”字形不规则截面导体，很难找到精确可靠的数学模型计算钢轨交流内阻抗，文献[6，8，10]提出可以将钢轨等效为管状导体模型来计算内阻抗，基本原理见图2。

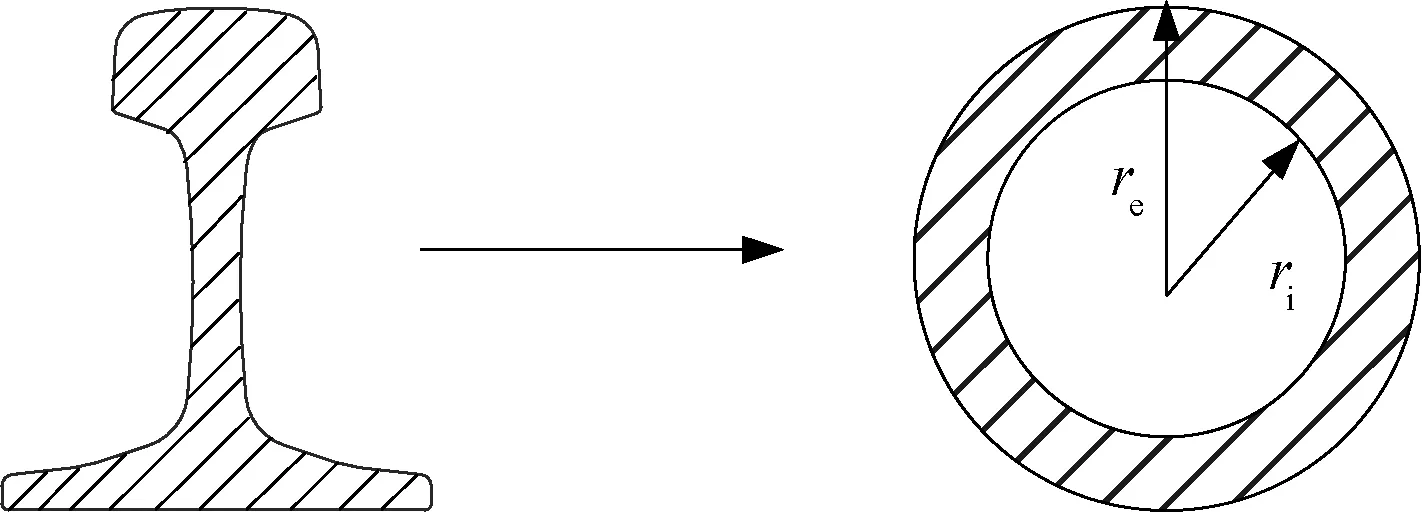
图2 钢轨等效管状导体模型

根据式( 1 )和式( 3 )可知，钢轨等效管状导体需要确定4个关键参数：钢轨等效管状导体电导率σ、等效管状导体磁导率μ、等效管状导体外径re、等效管状内径ri。

1.2 管状导体内阻抗的数值计算

式( 1 )、式( 3 )中的Kelvin函数计算繁琐，且文献[7-8]发现在参数mr>80的情况下，结果会出现振荡、不可靠。这是因为钢轨的高磁导率而导致mr过大引起振荡。文献[7]利用标记法简化式( 1 )，文献[13]将Kelvin函数用余弦函数和多项式函数近似，降低了计算复杂性。本文将式( 1 )表达为Bessel函数形式，如式( 5 )所示。使用多项式函数以及余弦函数进行简化，适用范围|x|>4，相对误差为10-9数量级，得到的内阻抗精度非常高，能满足大部分计算需求[14-15]，并且易于编程。

( 5 )

( 6 )

式中：J0和J1分别表示0阶和1阶的第一类Bessel函数; K0和K1分别表示0阶和1阶修正的第二类Bessel函数。

2 钢轨等效管状导体模型参数的确定

虽然管状模型计算精确且易于编程计算，但是在计算过程中难以确定关键参数。为此在实验室建立钢轨交流内阻抗测量平台，实测钢轨不同频率电流激励下的阻抗，利用不同频率下的钢轨阻抗测试数据拟合钢轨等效管状导体的关键参数。

2.1 钢轨不同频率内阻抗测量

为准确获得P60钢轨不同频率内阻抗，在实验室建立如图 3所示的测试系统，该系统主要是由大功率可编程交流电源，1 Ω精密、无感、大功率定值电阻，置于绝缘垫上的1 m待测钢轨和信号采集装置组成。

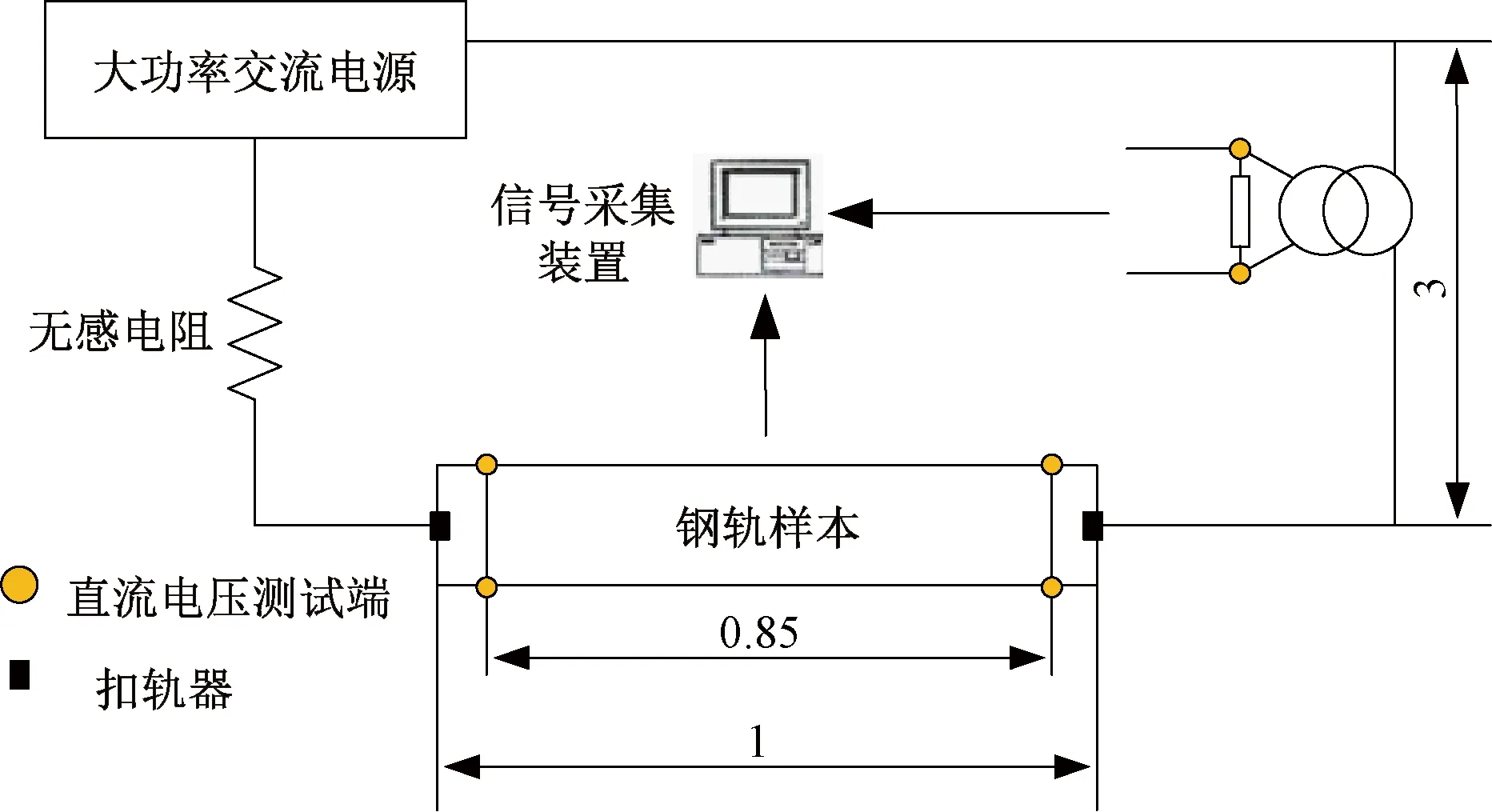
图3 钢轨交流内阻抗测量原理(单位：m)

大功率可编程交流电源注入0～5 000 Hz，20 A、电流精度小于0.2%的电流信号。为了确保电压测量精度尽可能高，信号采集装置要求达到采样频率50 kHz，采样位数为24位且支持多通道采集和精确调节增益功能。

测量导线和电源回路连接导线会对测量信号产生电磁干扰，需要将测量导线和连接导线均穿过独立铜管进行电磁屏蔽。经过多次试验验证，当连接导线位于距钢轨3 m以外的位置时，可以避免电磁干扰的影响。

为了避免接触电阻的影响，试验中采用四点法对图 3中0.85 m钢轨纵向电压进行测量。受限于实验室内钢轨长度较短，注入电流在钢轨内分布不均匀会影响钢轨交流内阻抗测量结果。通过同步测量钢轨内外侧表面纵向电压降落取平均值，以减少因轨中电流分布不均匀而引起的测量偏差。

试验注入20 A不同频率的电流，得到不同频率下钢轨纵向电压降落的幅频特性、相频特性见图4，根据图 4可以看出，随着频率的增大，钢轨纵向电压降落幅值增加，相角减小。利用图4中的测试结果，计算得到单位长度钢轨交流内阻抗见图5。

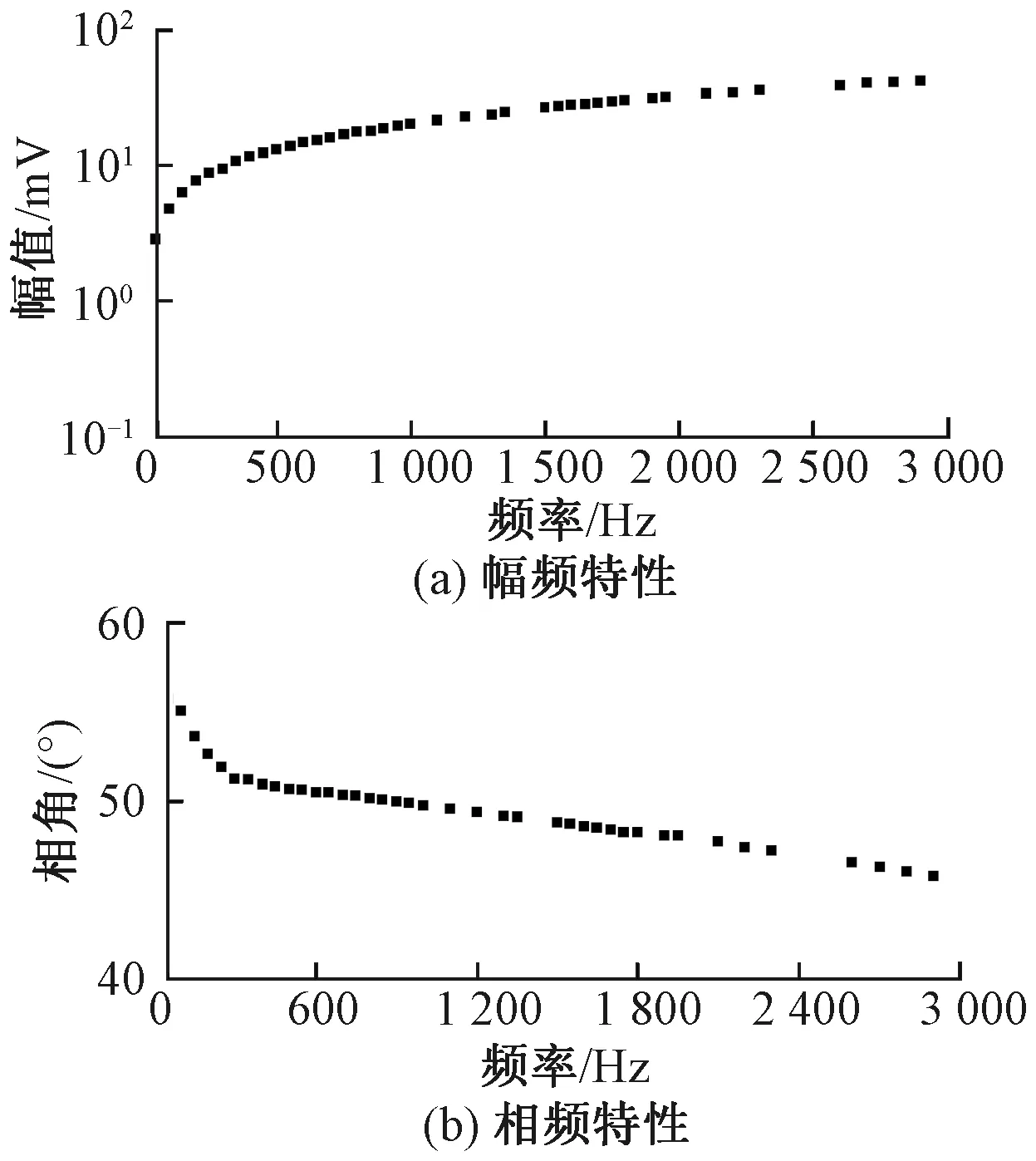
图4 P60钢轨纵向电压降落的幅频特性、相频特性

由图 5可以看出，由于集肤效应，频率越大，折算至单位长度的钢轨电阻和电抗越大；3 000 Hz情况下的交流内阻抗相较于直流电阻增加了40倍左右。

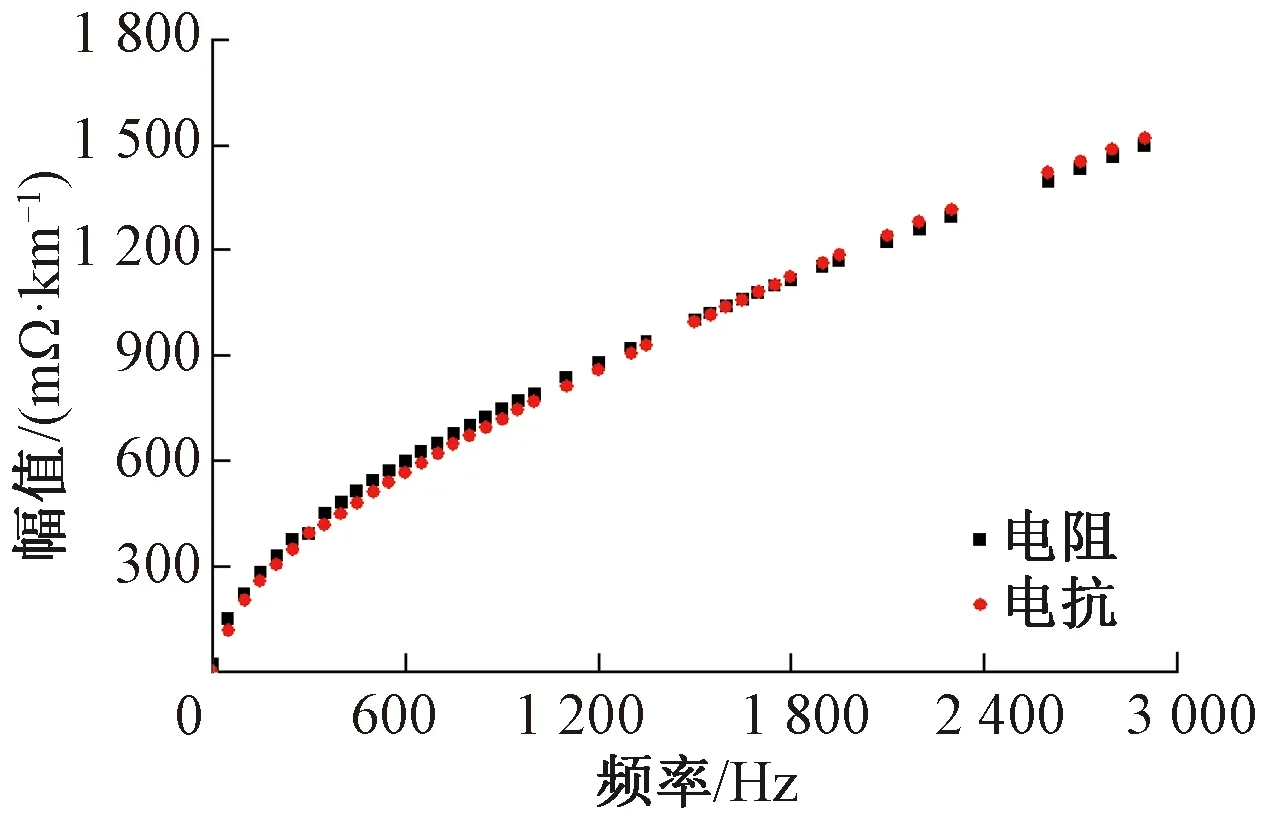
图5 P60钢轨实测交流内阻抗

2.2 钢轨管状导体模型参数确定

根据实测典型频率下的钢轨交流内阻抗数据和管状导体内阻抗计算模型，拟合钢轨等效管状导体模型参数。为了在一定约束下，计算结果Zr和实测结果Zi的差值达到最小，构建最小误差的数学模型为

( 7 )

利用最小二乘法得到μr= 249.79，σ=1.281×106S/m，re=0.165 m，ri=0.145 m。模型计算结果与实测对比见图 6。采用Pearson(皮尔逊)相关系数[16]以及相对误差δ评估计算结果和实测结果。折算至单位长度电阻和电抗的Pearson系数分别为0.998、0.996，相对误差分别为7.53%、7.27%，由此可以看出确定管状导体模型参数后，其计算结果和P60钢轨典型频率下的内阻抗实测结果吻合度较好。

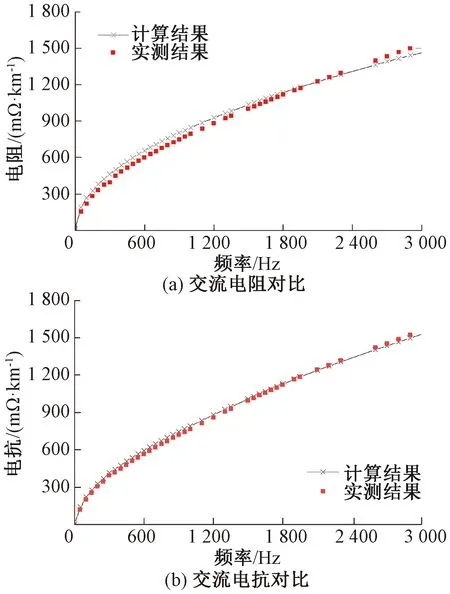
图6 钢轨交流内阻抗计算结果与实测结果对比

3 考虑阻抗频率特性的钢轨电位计算

3.1 直流牵引供电结构轨-地回路电气解耦

考虑地铁隧道内两行钢轨相对独立且距离较远，可以忽略两行钢轨之间的影响。列车电流由接触网注入一行的两根钢轨时，隧道段结构示意见图7。图7中，ir为单根钢轨上流过的电流。

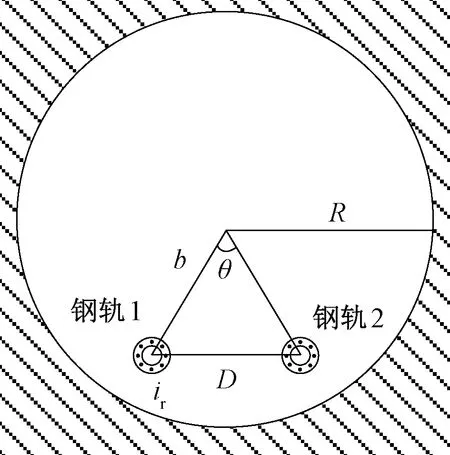
图7 四周无限大的圆形隧道模型

当一行钢轨通以大小相等，方向相同电流情况下，单位长度单根钢轨外电感Le为

( 8 )

钢轨-钢轨之间互感Mrr为

( 9 )

钢轨-钢轨间电容Crr为

(10)

钢轨-地间电容Cre为

(11)

式中：D为钢轨间间距；R为隧道等效半径；b为钢轨中心至隧道中心的距离；θ为钢轨1与钢轨2在圆形隧道中的夹角；ε为真空介电常数。

根据电磁场理论，将两根单位长度平行钢轨等效为管状导体后，在轨距D下会产生互感、电容，进行解耦，见图8。

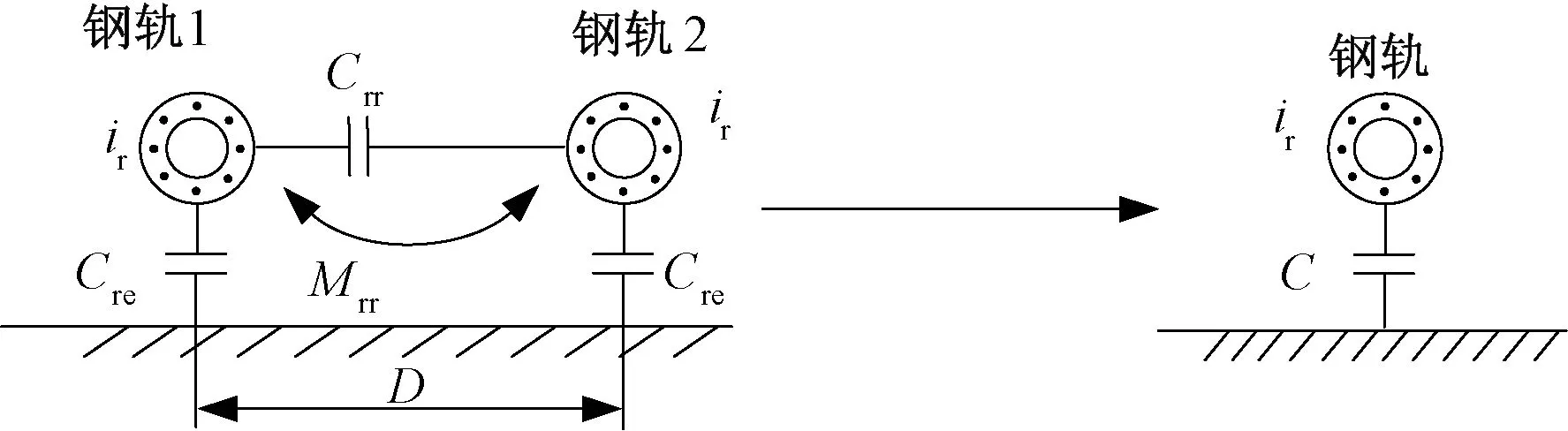
图8 轨-地回路电气解耦示意

Le、Mrr解耦得到一行钢轨等值电感L为

(12)

Crr、Cre等效在一行钢轨对地均匀电容C为

(13)

3.2 典型频率下钢轨电位计算

考虑列车注入电流含有多种频率成分。假设钢轨位置x处，频率ω下的电流向量为I(x,ω)，钢轨对地电压向量为U(x,ω)，位置x+dx处为I(x+dx,ω)、U(x+dx,ω)。解耦后一行钢轨的等值电路如见9。图9中，单位长度一行钢轨与地之间的电导为g；频率ω下单位长度一行钢轨电阻和电感分别为Rr(ω)和L(ω)。

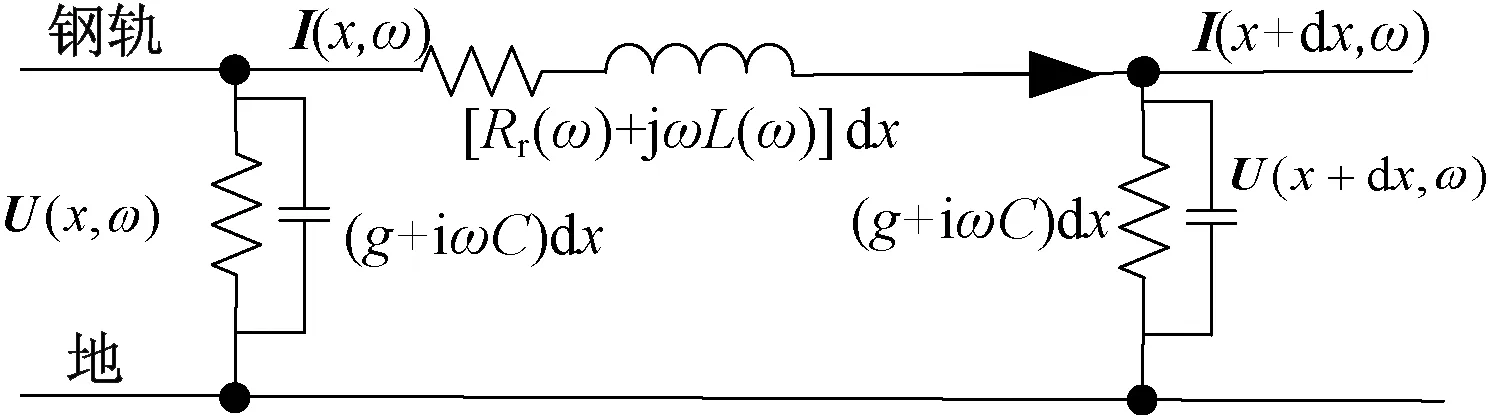
图9 解耦后一行钢轨分布式参数电路

图9中钢轨位置x处，U(x,ω)、I(x,ω)根据Kirchhoff定律可得

(14)

(15)

式中：C1、C2为根据边界条件确定的系数。

假设当x=0时，有如下边界条件。

(16)

式中：U1为x=0位置处钢轨电位在频率ω下的电压向量;I1为x=0位置钢轨电流在频率ω下的电流向量。

综合求得频率ω下位置x处的U(x,ω)、I(x,ω)为

(17)

根据端口网络等值的方法得到一行钢轨-地回路集中参数模型，在频率ω下，长度L的钢轨纵向电压降落ΔU(L,ω)为

ΔU(L,ω)={cosh[λ(ω)L]-1}U1+

Zc(ω)sinh[λ(ω)L]I1

(18)

3.3 考虑轨中电流频率成分后的钢轨电位计算方法

考虑轨中电流频率成分后的钢轨电位计算步骤如下：

Step1在多个牵引变电所、多车的复杂工况下计算钢轨电位极其复杂，根据叠加原理可以将复杂工况拆解为多个单边供电工况。

Step2单边供电工况下，当已知列车时刻t、位置x处的轨中电流为ir(x,t)时，对列车电流进行傅里叶变换，得到各次频率下列车位置的电流向量Ir(x,ω)为

Ir(x,ω)=F[ir(x,t)]

(19)

式中：F(·)为傅里叶变换。

Step3在单边供电工况下，确定边界条件为

Ir(0,ω)=Ir(L,ω)

(20)

式中：L为单边供电工况下牵引变电所和列车的间距。

Step4将各次频率下的电流向量Ir(x,ω)和钢轨内阻抗Zr(ω)代入式(18)，得到各次频率下、长度L的钢轨纵向电压降落向量ΔU(L,ω)和x=L处的钢轨电位向量U(L,ω)为

(21)

Step5对各次频率下的ΔU(L,ω)和U(L,ω)进行傅里叶逆变换，得到长度为L的钢轨纵向电压降落时域Δu(L,t)和牵引变电所x=L位置处钢轨电位时域u(L,t)分别为

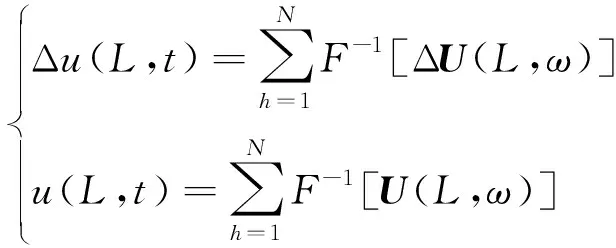
(22)

式中：N为频率数量；F-1(·)为傅里叶逆变换。

Step6根据叠加原理计算多个列车、多个牵引变电所的复杂工况下全线各位置钢轨电位。

4 工程算例

4.1 实验室平台钢轨纵向电压降落算法验证

为了验证钢轨电位计算算法的正确性，根据3.1节获得的P60钢轨交流内阻抗，用大功率可编程交流电源发出如图 10所示的多组6倍频谐波电流叠加信号，在0.85 m钢轨产生的纵向电压降落见图10。

图10 6倍频谐波电流、纵向电压降落波形

考虑实验室平台工况，计算条件满足式(23),将式(23)代入式(18)，计算实验室平台工况下的钢轨纵向电压降落。分析得到实测I(0,ω)、实测ΔU(L,ω)和计算ΔU(L,ω)中包含的6倍频谐波分量幅值为

(23)

6倍频谐波分量幅值见表1。

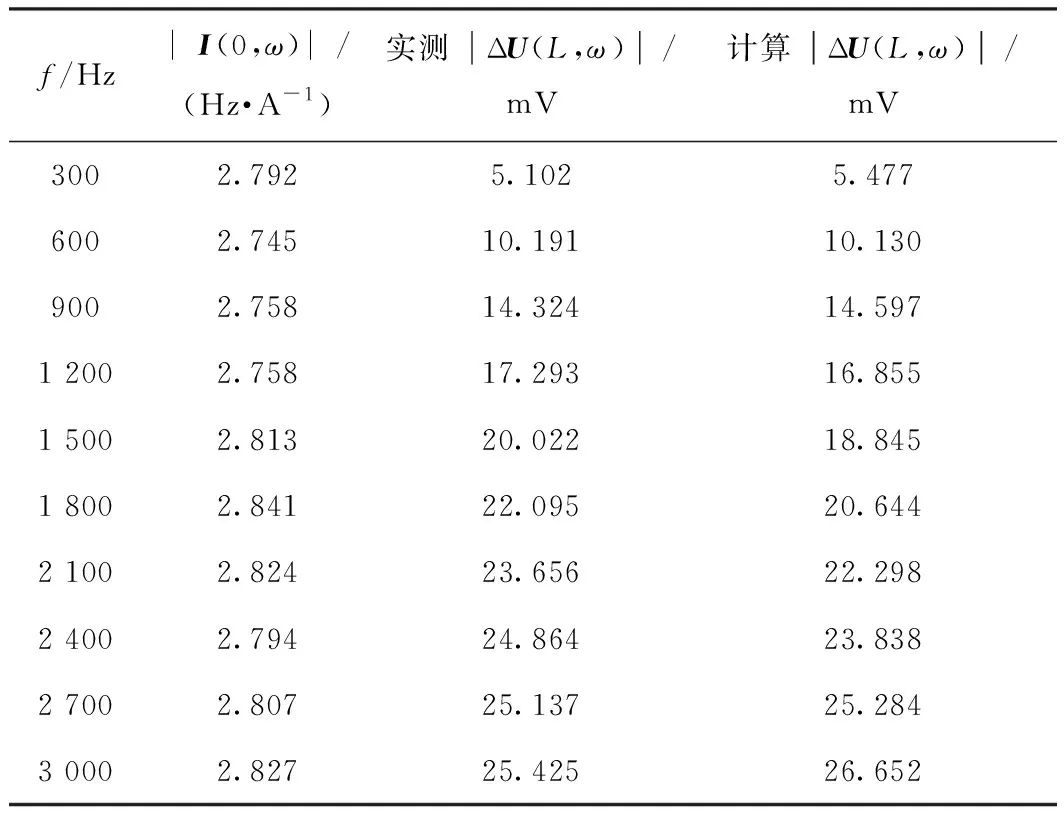
表1 6倍频谐波电流、钢轨纵向电压降落典型频率幅值

根据表 1可以看出，典型频率下的纵向电压幅值随着频率的增大而增大。计算|ΔU(L,ω)|中6倍频电压典型频率幅值与实测值的相对误差最大为9.12%。

计算Δu(L,t)和实测Δu(L,t)波形见图 11。两曲线的Pearson相关系数为0.991，相对误差小于7.59%，验证了本文计算方法的有效性。

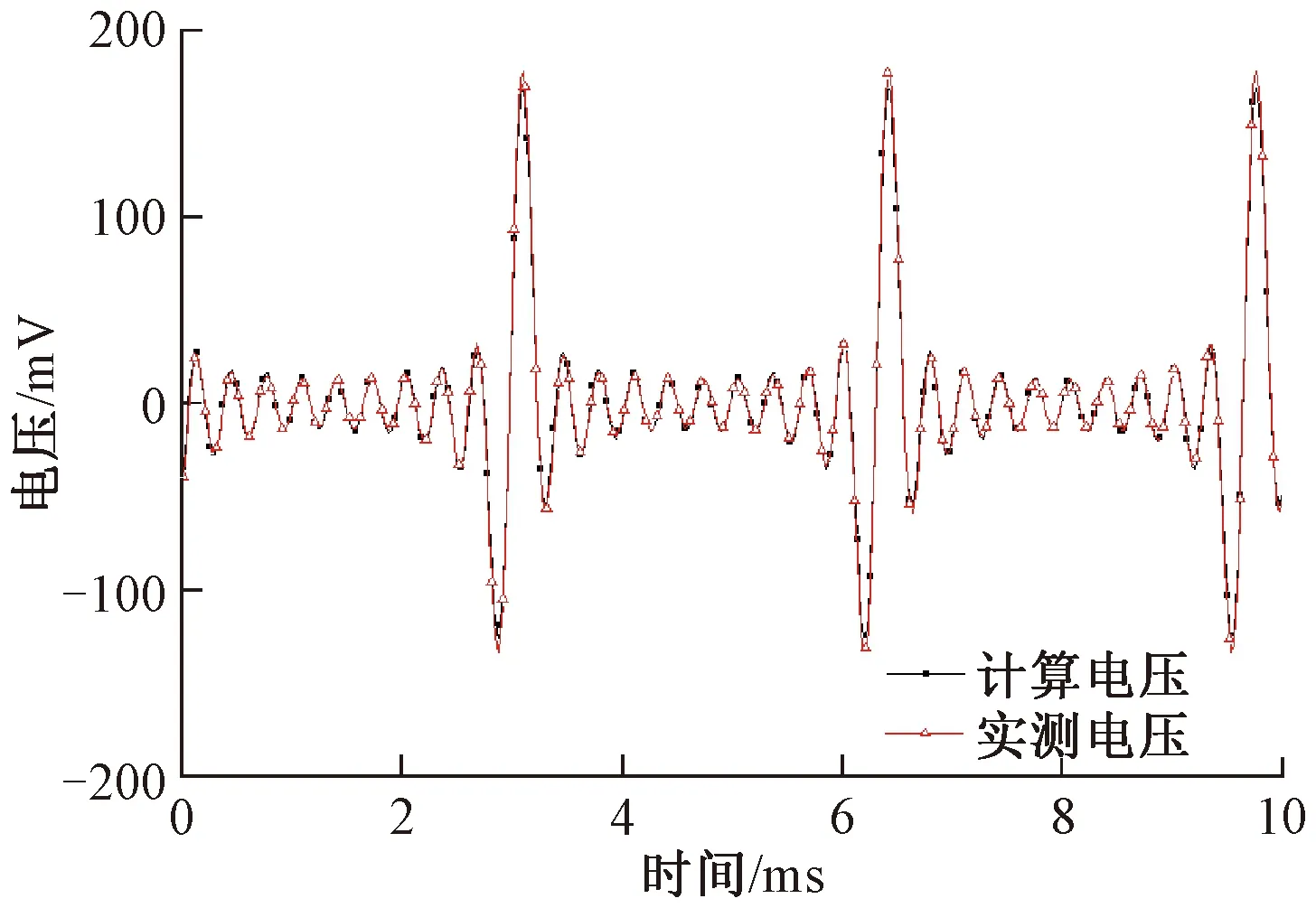
图11 计算纵向电压和实测纵向电压降落对比

4.2 单边供电时钢轨电位计算的工程验证

以某运营地铁P60钢轨线路L=1.88 km的区间为测试案例。该区间位于线路末端牵引变电所和出入段线咽喉区之间。在牵引变电所安装馈线电流和钢轨电位测量装置，在咽喉区靠近正线一侧布置钢轨电位测量装置。不同位置测试信号用GPS同步对时。

在收车阶段最后一列车通过该区间时，末端牵引变电所的馈线电流为列车取流；以电缆支架上的贯通扁钢为参考地，牵引变电所OVPD与咽喉区钢轨电位之差即为长度L的钢轨纵向电压降落。监测点系统图见图12，列车取流i(0,t)见图13。

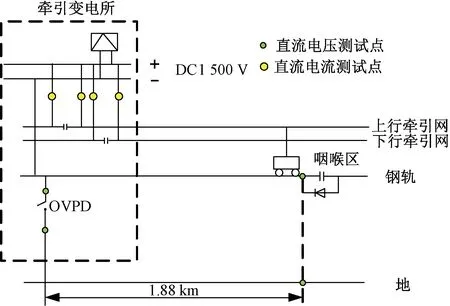
图12 单边供电系统示意

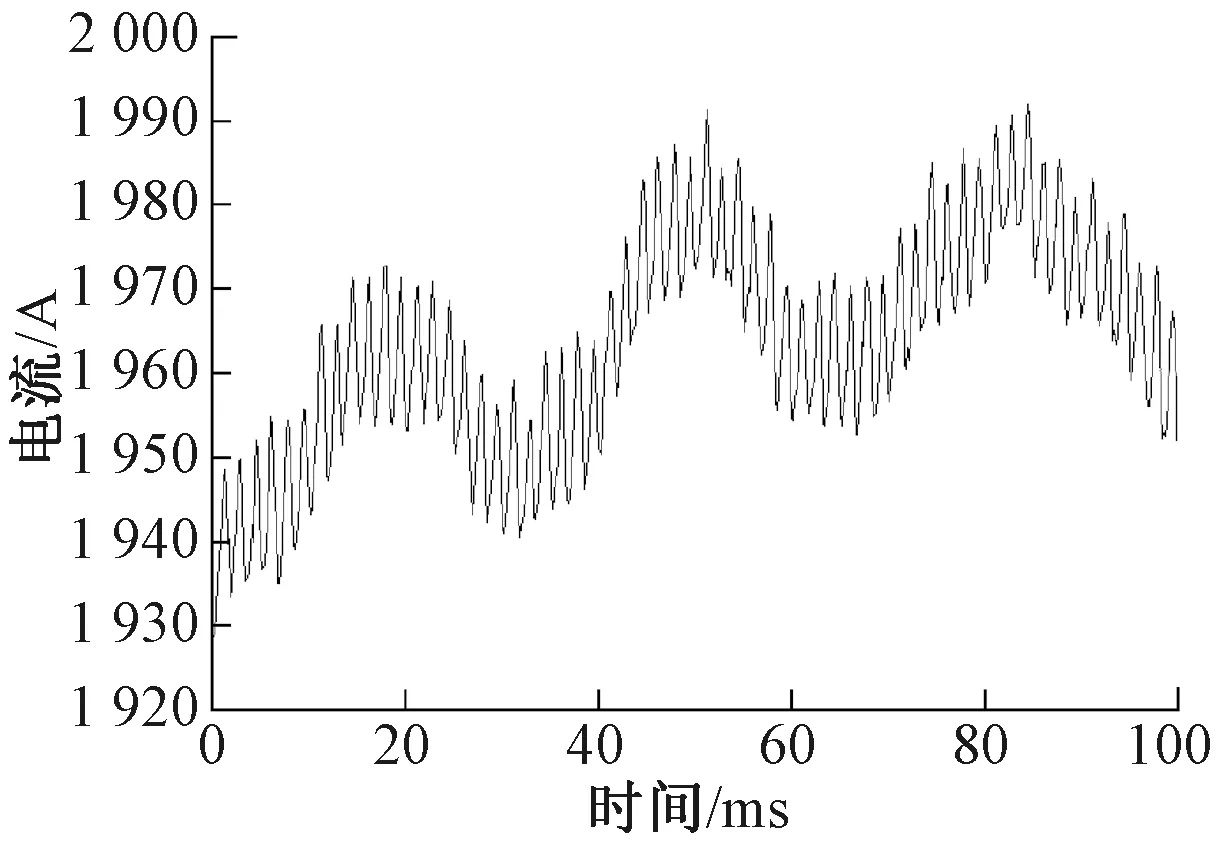
图13 某地铁单车负荷电流

对图 13中的电流进行傅里叶分解得到的频谱见图14。由图14可见，列车负荷电流中包含大量1～50 Hz低频分量以及少量6倍频分量。

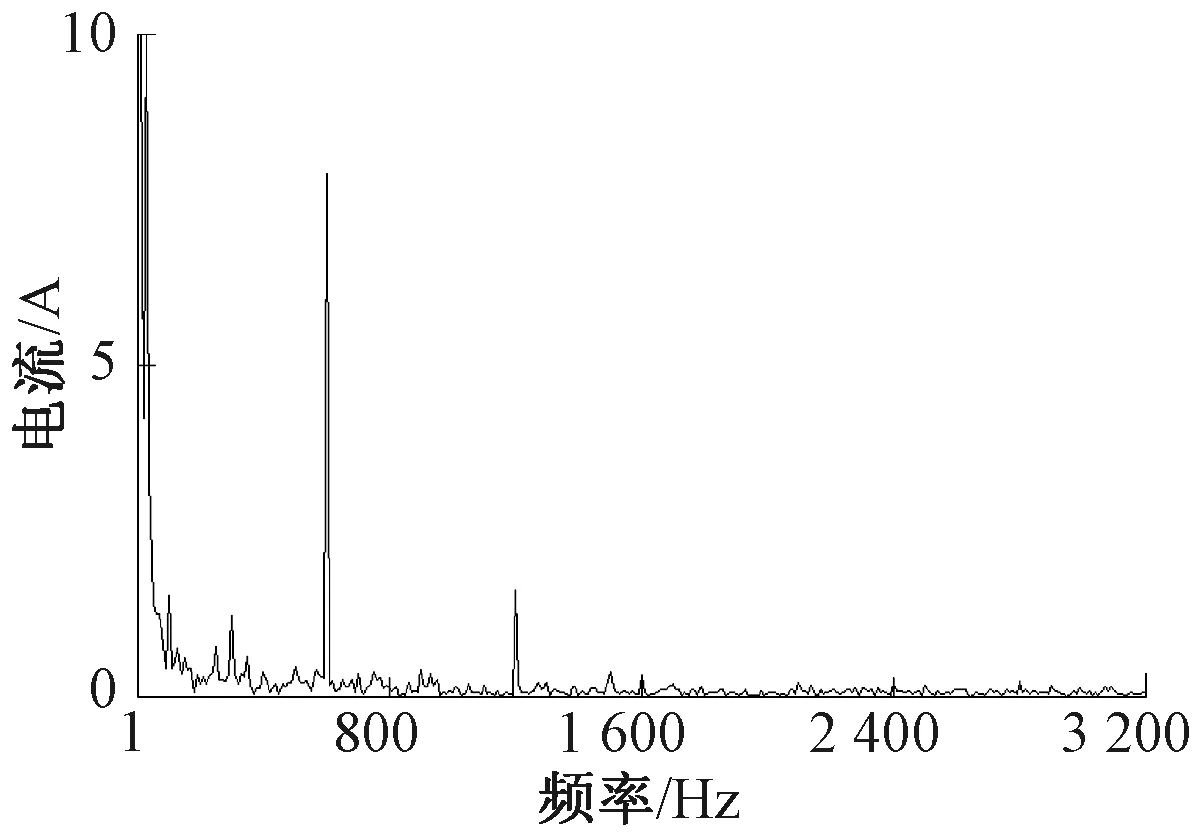
图14 负荷电流频谱

分别在Case A(仅考虑单位长度直流电阻)，Case B(考虑钢轨阻抗频率特性)两种情况下，计算Δu(L,t)和u(L,t)，计算参数见表2。

表2 计算参数设置

Case B中计算Δu(L,t)和实测Δu(L,t)的误差见图15。由图15可见，两曲线的Pearson相关系数为0.922，相对误差小于9.17%。

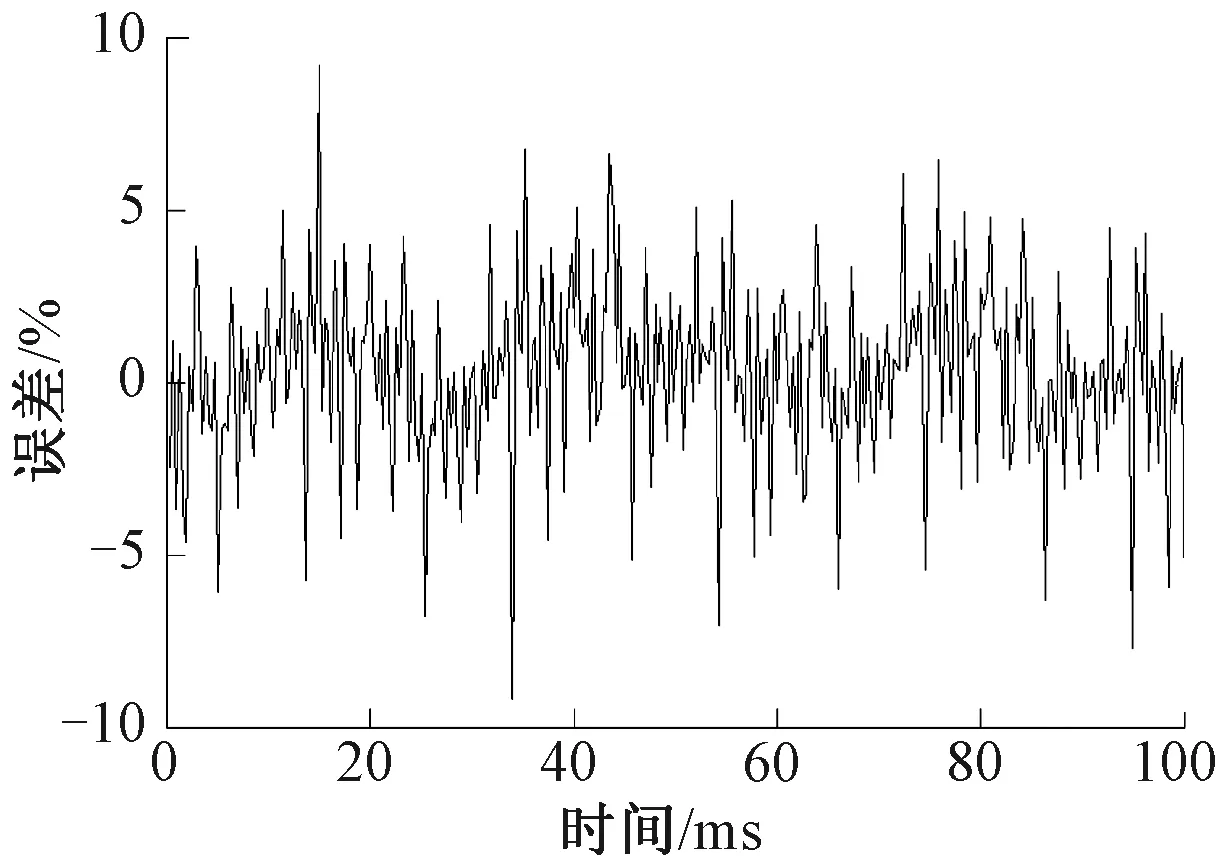
图15 计算和实测钢轨纵向电压降落误差

Case B中计算u(L,t)的频谱见图16。统计得到的i(0,t)、u(L,t)的典型频率成分见表3。

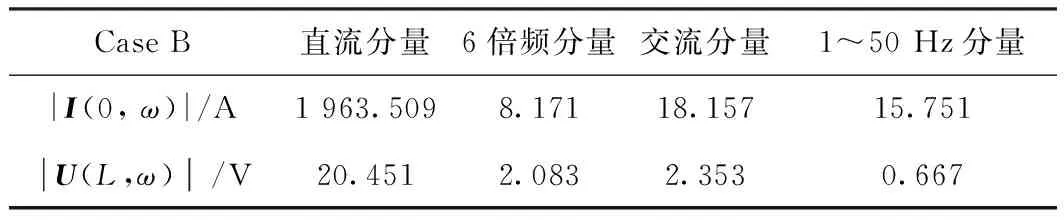
表2 某地铁i(0,t)、u(L,t)典型频率成分

由表3可见，列车负荷电流中6倍频分量占交流分量的20.25%，1～50 Hz分量占比达到75.24%。Case B中6倍频分量占总交流分量的78.37%，1～50 Hz分量仅占到8.04%。诚然，轨中电流成分含有丰富的1～50 Hz分量和部分6 倍频分量，但是在传输过程中，经过钢轨阻抗频率特性的作用，呈现于钢轨纵向电压降落成分中的6倍频分量增加了58.12%，1～50 Hz降低了67.2%。

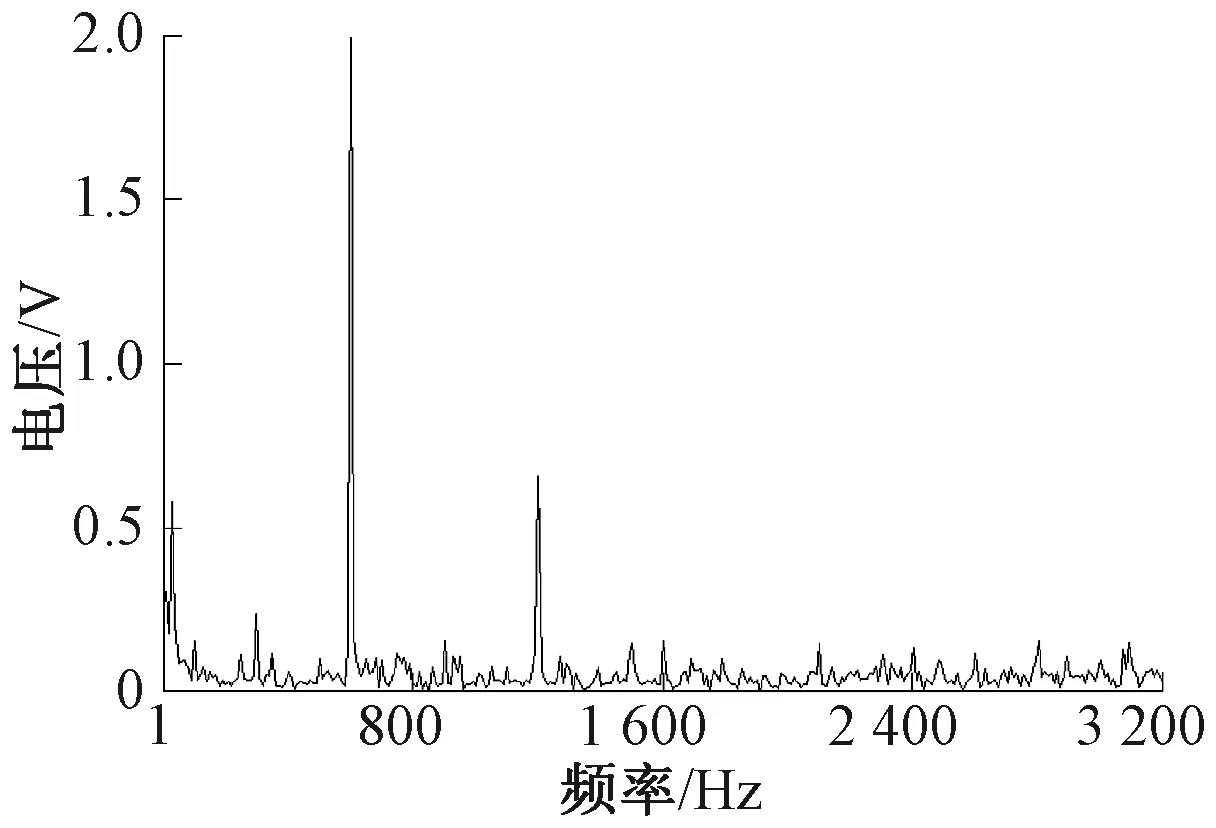
图16 牵引变电所u(L,t)频谱

对比分析CaseA、CaseB两种情况下，100 ms内u(L,t)波形见图17。由图17可见，只考虑直流电阻的u(L,t)分布相对稳定；考虑钢轨阻抗频率特性后，u(L,t)分布波动频繁且剧烈；最大值增加了24.27%，最小值降低了18.60%。

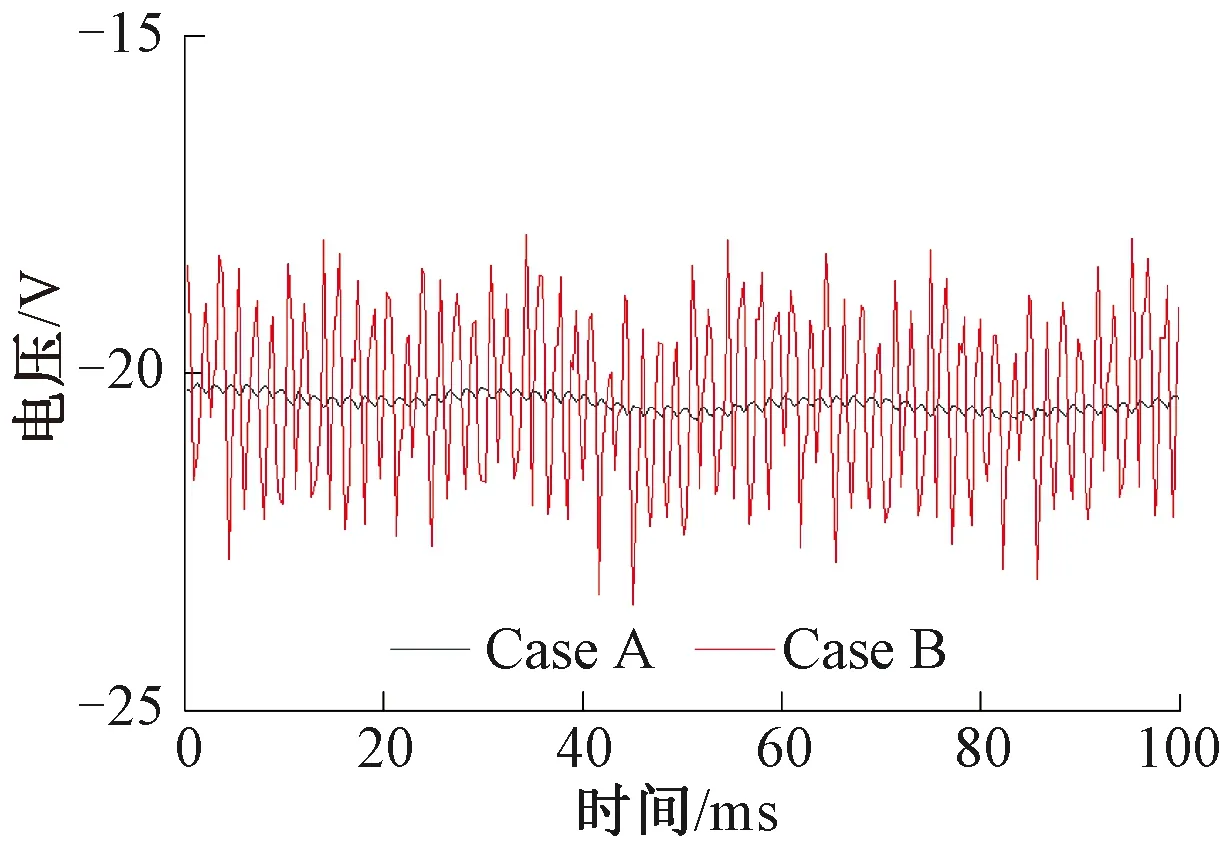
图17 两种计算方法u(L,t)对比

5 结束语

本文提出了考虑钢轨等效管状导体模型和轨中电流频谱的钢轨电位计算方法。根据实测不同频率下的阻抗结果，拟合确定P60钢轨等效管状导体参数。对直流牵引供电结构进行解耦，建立钢轨-地分布式参数模型，提出复杂工况下钢轨电位的计算方法。通过实验室和工程案例验证了方法的准确性。

地铁列车注入钢轨电流中含有丰富的1～50 Hz分量和部分6 倍频分量。这部分回流在传输过程中，经过钢轨阻抗频率特性的作用，呈现于钢轨电位成分中6 倍频分量影响更大。

在城市轨道供电系统中，受列车注入电流频谱分布的影响，采用计及钢轨阻抗频率特性的计算方法，钢轨电位的计算结果更接近实际。钢轨电位的计算对准确分析城市轨道供电屡屡发生的异常钢轨电位问题(尤其是OVPDⅡ段动作)、抑制钢轨电位措施的研究有着重要的意义。