严重初始延误与区间限速条件下高速列车实时调度模型

王铭铭，王 莉，许心越，秦 勇

(1.北京交通大学 交通运输学院, 北京 100044；2.北京交通大学 轨道交通控制与安全国家重点实验室, 北京 100044)

面向突发事件下列车实时调度优化问题是考虑突发事件影响，对已发布执行列车运行计划的实时调整。随着列车运行速度提高、开行密度增大，突发事件下列车运行计划调整问题已逐渐成为铁路运输组织的研究热点[1]，但现有研究主要集中于扰动情景下的列车日计划调整，面向大面积列车晚点和区间限速等严重复合场景下高速列车实时调度问题还未得到较好地解决，是现场调度亟需解决的问题之一。本文针对严重初始延误和区间限速情况下列车实时调度优化方法进行研究。

突发事件可分为轻微扰动和严重扰动[2]。轻微扰动下列车实时调度优化主要针对列车发生轻微初始延误场景，文献[3-5]从微观层面采用替代图刻画列车运行逻辑关系，建立面向轻微延误的列车运行调整模型，但模型复杂度随研究场景复杂程度呈指数增长，无法解决大规模严重扰动问题[6-7]。严重扰动下的列车实时调度称为扰动管理，现阶段研究主要针对单一扰动场景进行调度优化。文献[8-10]针对周期运行图采用事件活动网络构建列车运行调整模型，处理线路中断情况下的列车运行调整问题。文献[11]提出单线铁路区间能力失效条件下的列车运行调整模型，并设计不确定性分枝定界求解算法。文献[12-14]针对区间完全或部分中断情况，基于事件活动网络提出列车运行调整模型。文献[15]研究区间突发故障中断下的列车运行调整问题，建立混合整数线性规划模型。上述文献仅针对区间完全或部分中断单一场景进行研究，严重初始晚点和区间限速等并发场景造成大面积列车连带晚点，影响时空范围更广、需要调度列车多，这使得调度场景更加复杂、约束耦合更强、全局调度优化问题更加困难。

面向突发事件的列车实时调度问题属于NP-hard问题，模型求解时间随问题规模扩大而增加，因此相关学者也致力于求解算法的研究。面向新增列车运行线情况，文献[16]提出基于ADMM(Alternating Direction Method of Multipliers)的运行图优化算法。文献[17]针对双线铁路运行调整问题，提出禁忌搜索算法，以列车晚点最小为目标，搜索受影响列车的最优运行顺序。文献[18]提出遗传和粒子群混合启发式算法，求解轻微初始延误下的列车运行调整模型，但在可接受时间内获得可行解与最优解差距19.6%。文献[19]针对列车变更运行径路情况，提出列车运行调整的分支定价算法，但仅探讨了小规模算例的适用性。文献[20]针对轻微延误情况，提出基于分阶段多叉树的延误列车运行优化调整算法，实现列车总延误最小。

上述文献大多数采用启发式算法求解，大规模算例情况下并未获得最优解，综上，严重影响下列车实时调度优化问题研究尚比较缺乏，且目前我国采用非周期性运行图，运输组织模式更加复杂，国外相关研究成果不适用于我国严重突发事件下列车实时调度问题。此外，符合我国高速铁路特性的面向严重初始延误与区间限速的列车实时调度优化模型，且能够运用于调度现场辅助决策的研究成果不足。

本文将模型复杂非线性约束以中间决策变量线性化为析取不等式约束组，采用分枝定界算法，在满足实时性情况下，获得最优列车调度方案，基于文献[12-13, 21]，针对严重初始晚点和区间限速场景，从宏观层面构建事件活动网络，考虑调整后列车调度方案与原列车调度方案的偏离程度最小化，提出列车实时调度优化模型相关约束和目标函数的线性化方法；实例验证所提出模型算法的有效性，并将所提出模型算法嵌入现场调度辅助决策系统中进行应用，实现严重初始晚点和区间限速情况下的列车实时调度。

1 问题描述与界定

1.1 问题描述

大面积列车晚点、单列车发生较大晚点和长时间区间限速波及列车多、影响时间久，降低列车运输服务质量、影响行车安全，需要对在途和当日计划运行列车进行实时调度。事件活动网络示意见图1。

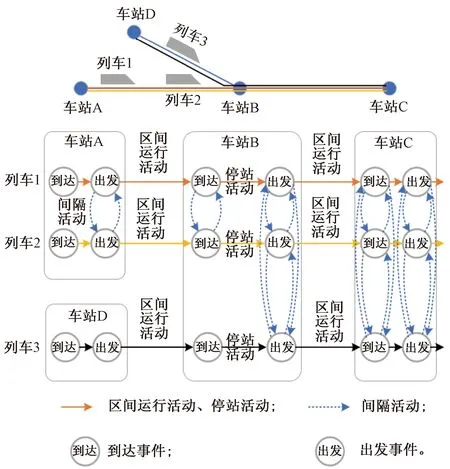
图1 事件活动网络示意

图1中，当区间(车站1，车站2)发生长时间限速，列车G3、G5、G7、G9、G11直接受到影响，不能按照计划运行图运行。因此，需要实时调度运行图中列车，所需调度列车不仅受到列车在区间最小运行时分、列车最小停站时分和列车最小运行间隔时分等基本相关约束的制约，还受已发布执行列车运行图和突发事件影响的限制。在满足上述众多约束情况下，调整受影响区段上列车途经各站的到发时刻、决策列车在冲突时空范围的最佳运行顺序和停运列车，最大程度降低列车调度方案与原列车运行计划的偏离程度。

1.2 问题界定

在突发事件条件下，列车实时调度是一项复杂工作，为简化研究问题，根据高速铁路调度现场作业，提出假设如下：

(1)为保证全线列车实时调度，将车站刻画为具有能力的节点，车站能力用车站到发线数量表征，不详细研究车站到发线运用方案。

(2)仅考虑严重初始延误和区间限速时空范围已知，未受突发事件影响时段和区段，高速列车基本按图正常行车，不研究严重初始延误和区间限速对动车组运用计划的影响。

2 模型构建

2.1 问题抽象

采用事件活动网络表征列车运行逻辑关系。在事件活动网络中，事件表示列车在其途经各车站的到达或出发事件节点，活动是连接两个相关联事件的有向弧段，详细描述参考文献[13]。图1为3趟列车在路网的事件活动网络，列车1和2的运行径路是{车站A，车站B，车站C}，列车3的运行径路是{车站D，车站B，车站C}。在突发事件情况下，需要决策事件活动网络中各列车事件的发生时刻、相邻列车在其运行冲突径路上事件的发生顺序和列车事件是否取消，从而降低突发事件对列车运行计划的影响，保障列车运行安全和服务质量。

2.2 模型参数与决策变量

参数及含义见表1。

表1 模型参数

ωe为整数决策变量，表示调整后事件e发生时刻；ce为0-1决策变量，事件e被取消为1，否则为0；o(ei,ej)为0-1决策变量，事件ei早于事件ej为1，否则为0 。

2.3 模型建立

面向突发事件影响高速铁路列车实时调度的主要目的是能够快速恢复列车按图行车，尽可能减少调整后列车调度方案与列车运行计划的偏离程度。偏离程度可用调整后列车在计划停车站的到发时刻与计划时刻的偏差和取消列车数量衡量。

(1)目标函数

目标函数为

(1)

(2)

式(1)表示与列车运行计划时刻偏差最小化；式(2)表示取消列车数量最小化。

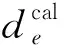
(3)

(2)列车运行计划时刻偏差约束

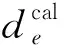
de≥ωe-pte

e∈e{r,s,l|r∈T,s∈Rr,l∈{dep,arr}}

(4)

de≥-(ωe-pte)

e∈e{r,s,l|r∈T,s∈Rr,l∈{dep,arr}}

(5)

e∈e{r,s,l|r∈T,s=Rr,l∈{arr,dep}}

(6)

T,s=Rr,l∈{arr,dep}}

(7)

e∈e{r,s,l|r∈T,s=Rr,l∈{arr,dep}}

(8)

(3)列车取消约束

为避免取消列车对旅客造成较大的影响，该模型仅在列车始发站决策该列车是否取消。列车在始发站的出发晚点超过晚点容忍阈值DTtoler，该列车取消。

de-DTtoler≥(ce-1)·Me∈e{r,s,l|r∈

T,s=or,l=dep}

(9)

所属同列车的事件取消决策与前一事件的取消决策一致，即同列车的后续事件取消决策取决于列车在始发站出发事件的取消决策。

ce=ce′

(10)

e∈e{r,s,l|r∈T,s=or,l=dep}

e′∈e{r′,s′,l′|r′=r,s′∈Rr,l′∈{dep,arr}}

(4)列车出发时刻约束

由于列车时刻表已向旅客发布，列车在计划停车站调整后的出发时刻，不能早于计划发车时刻。

ωe-pTe≥ce·Me∈e{r,s,l|r∈T,s∈or∪

(11)

(5)列车初始延误约束

由于突发事件造成大面积列车延误dte，发生初始延误的事件调整后的发生时刻不早于事件计划发生时刻与初始延误时间的总和。

ωe-pte≥ce·(M-dte)+dte

(12)

(6)区间限速约束

(13)

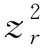
(14)

zr为列车是否受突发事件影响，具体取值为

(15)

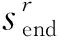
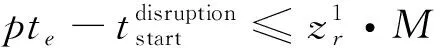
(16)

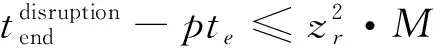
(17)

(18)

(19)

(20)

受突发事件影响的列车在事件影响时空范围内的区间运行时分增加，其增加程度取决于区间限速等级，根据高速铁路行车规则和突发事件下应急响应预案，确定列车在突发事件下的限速等级和区间运行时分增加程度θ。其具体约束为

(21)

(e,e′)=a∈Arun

(7)车站到发线数量约束

列车进站时，应至少存在一条空闲股道供列车停站或通过。根据列车到达车站顺序和从车站出发顺序，分别统计列车r′到达车站之前从同一方向到达该车站的列车数量和列车r′从该车站出发之前向同一方向出发的列车数量。为避免始发站列车无到达时刻和终到站列车无出发时刻，定义列车从动车段进入车站的时刻为始发站列车进入车站时刻，列车进入动车段的时刻为终到站列车从车站出发时刻。本文仅限定到发线数量约束，并不考虑到发线使用方案。

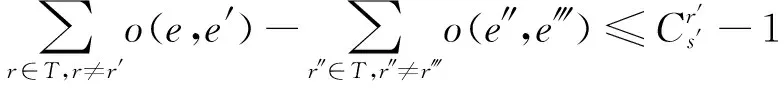
(22)

e∈e{r,s,l|r∈T,s=s′,l=arr}

e′∈e{r′,s′,l′|r′∈T,s′=Rr′,l′=arr}

e″∈e{r″,s″,l″|r″∈T,s″=s′,l″=dep}

e‴∈e{r‴,s‴,l‴|r‴=r′,s‴=s′,l‴=dep}

此外，为决策同一方向相邻列车相继到达同一车站时是否占用该车站同一到发线，引入决策变量：χ(e″,e′)为事件e″和事件e′是否占用相同到发线，具体取值为

(23)

e″∈e{r″,s″,l″|r″∈T,r″≠r′,s″=s′,l″=dep}

e′∈e{r′,s′,l′|r′∈T,s′=Rr′,l′=arr}

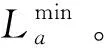
(24)

e″∈e{r″,s″,l″|r″∈T,r″≠r′,s″=s′,l″=dep}

e′∈e{r′,s′,l′|r′∈T,s′=Rr′,l′=arr}，

(8)其他约束

在满足上述约束条件下，同时也需要满足列车区间运行活动和停站作业时间约束、列车在站到发时刻逻辑约束和线路能力约束，并保证相邻列车无法在区间越行。

(25)

(e,e′)=aa∈Arun∪Adwell，

e∈e{r,s,l|r∈T,s∈Rr,l=dep}，

e′∈e{r′,s′,l′|r′=r,s′=sr,l′=arr}

或e∈e{r,s,l|r∈T,s∈Rr,l=arr}，

e′∈e{r′,s′,l′|r′=r,s′=s,l′=dep}

ωe′-ωe≥0

(26)

e∈e{r,s,l|r∈T,s∈Rr,l=arr}

e′∈e{r′,s′,l′|r′=r,s′=s,l′=dep}，

(e,e′)=a，a∈Astation

(27)

(28)

o(e,e′)+o(e′,e)=1

(29)

o(e,e′)-o(e″,e‴)=0

(30)

e‴∈e{r‴,s‴,l‴|r‴=r′,s‴=s″,l‴=l″} (e″,e‴)∈Arun

2.4 模型求解

由于模型包含大量0-1决策变量，因此采用分枝定界算法求解。该算法通过模型决策变量集合构建分枝定界搜索树，分枝定界搜索树用于表示分枝定界求解过程中树形结构，由节点和边两种元素组成，通过不断地分枝和剪枝过程，逐步寻求模型最优解。算法涉及的变量见表2。

表2 算法涉及参数

求解该模型的分枝定界算法步骤如下。

Step1初始化

根据模型决策变量，构建模型分枝定界搜索树的节点集合N，选取当前具有最小整数估计的节点为根节点，节点定义初始解上界LUB←+∞，g=0，Lg=∅。

Step2分枝过程

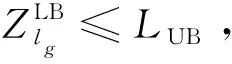
Step3剪枝过程

Step4终止条件

判断算法运行时间或模型上下界的差值是否满足预设定值，若满足，算法终止，模型所求解出的最小下界即为最优可行解；否则，进入Step2。

3 实例分析

3.1 实例描述

以2018年7月25日岳阳东站至广州南站的武广高速铁路区段的64对上下行高速列车运行计划与相关数据进行实际算例分析。研究区段沿线共经过14个车站，13个运行区间。为增加算例复杂程度，所选取列车具有不同的停站模式，并存在越行现象。

相关参数设置如下：为降低临时取消列车策略对乘客带来的负面影响，考虑取消列车数量在目标函数中的费用远大于列车在计划停车站的到发时刻总偏差费用，根据文献[22]设置目标函数费用wdiff=1 元和wcancel=1 000 元，列车在计划停车站的到发时刻总偏差费用和取消列车费用的详细分析见3.2.2节；假设列车取消阈值DTtoler为晚点时分1 800 s。相邻列车最小到达和出发间隔同为180 s；相邻同方向列车相继占用同一到发线的最小发到间隔时间为240 s。根据实绩列车运行数据，统计分析列车在区间最小运行时分，相应数值见表3；列车在计划停车站计划停站时分为列车最小停站时分，列车在非计划停车站的最小停站时分为0。车站能力参照“车站到发线数量”，其相应取值见表4，注意其值不包括车站正线数量。区间限速等级与区间最小运行时分增加程度θ的对应关系可参照参考文献[23]。原列车运行计划方案见图2。

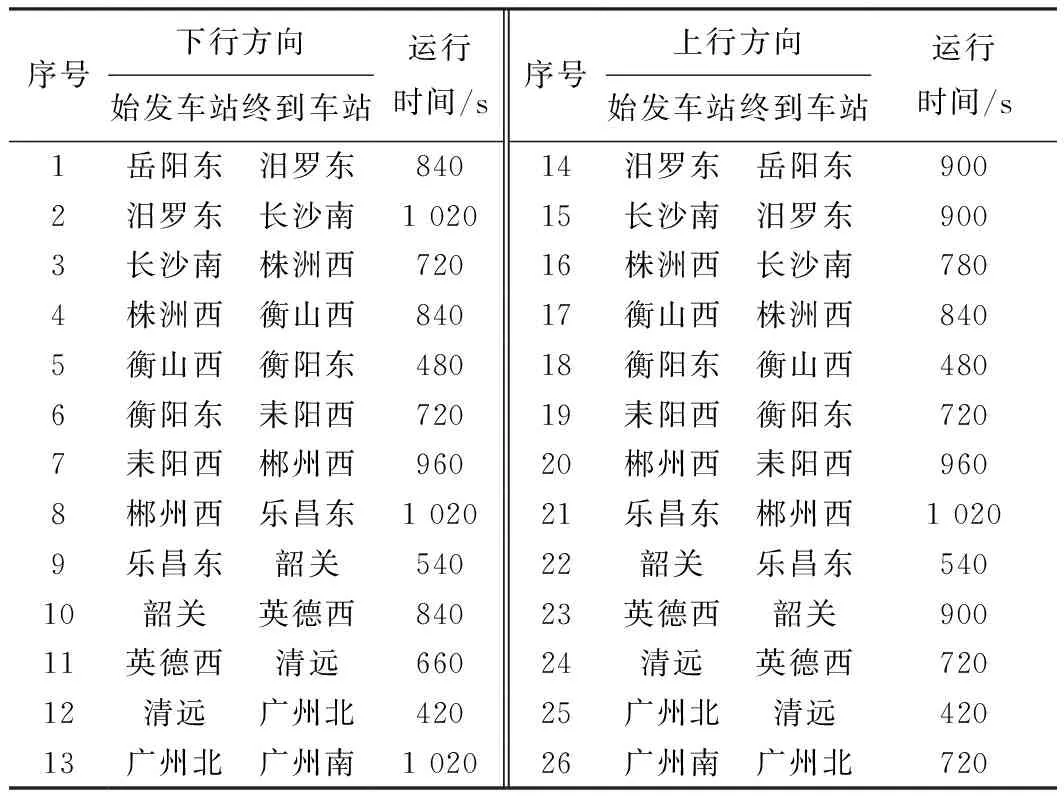
表3 区间最小运行时分(包括启停附加时分)

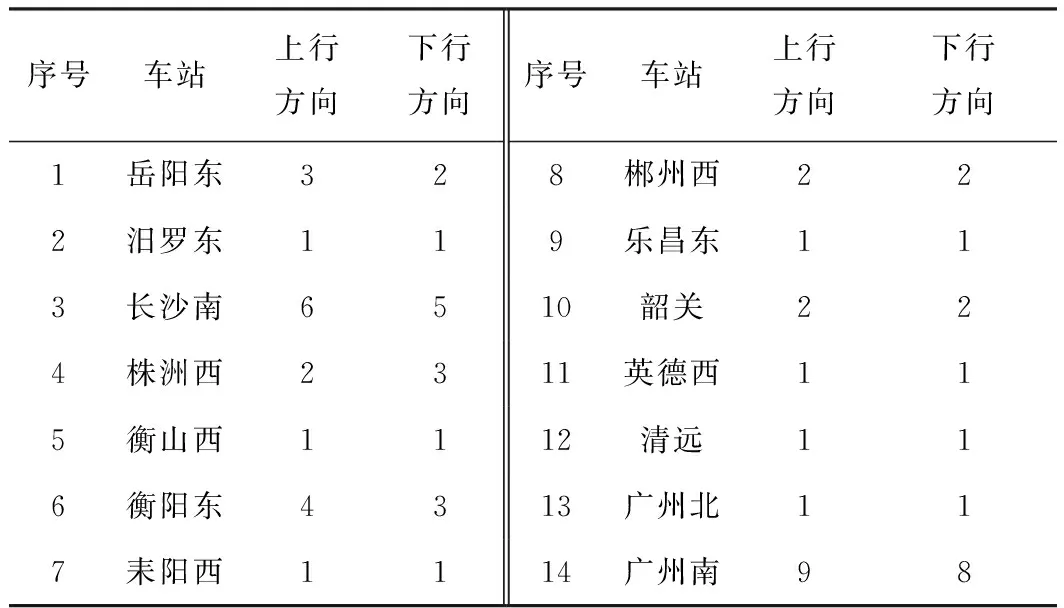
表4 车站到发线数量

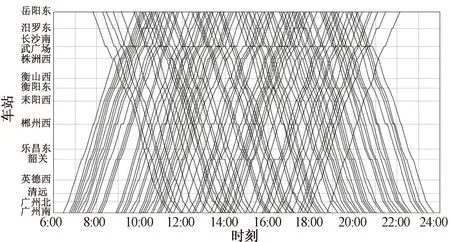
图2 原列车运行计划方案

为验证模型与算法对严重初始延误和区间限速场景处置的适用性和实时性，通过调整初始晚点和区间临时限速的时间和地点，设计了4种不同严重程度的突发事件场景。突发事件场景及其具体参数设置见表5。

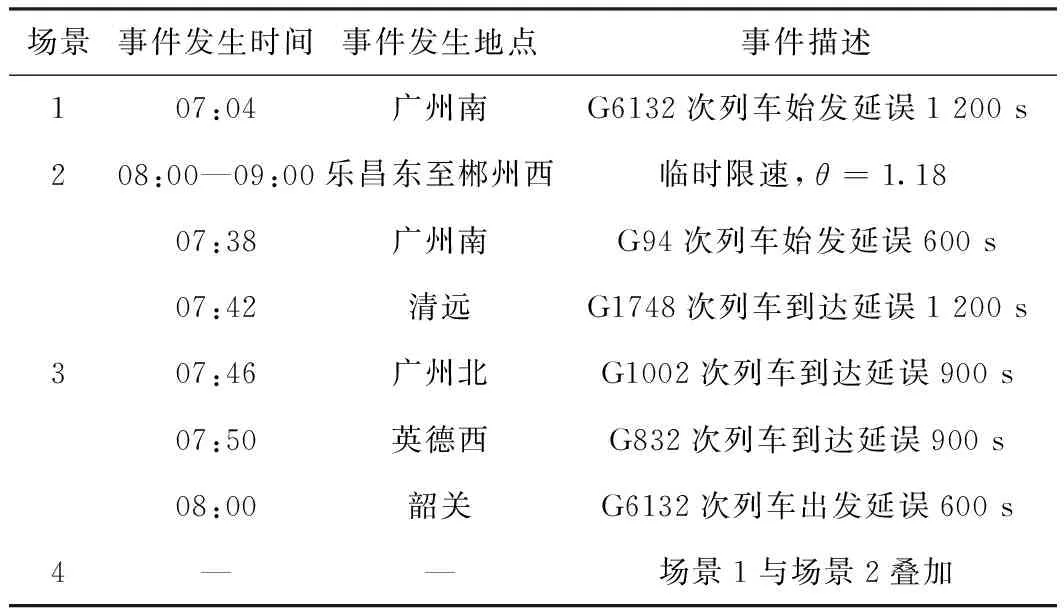
表5 突发事件场景参数设置

3.2 算例结果

本文算例实现环境：CPU为Inter (R) Core (TM) i7 10510U 2.30 GHz、内存16.0 GB、Windows 10的64位笔记本电脑，采用Python 3.6调用Gurobi 9.0.1编程，实现对所提出模型与算法进行实例验证。

3.2.1 可行性分析

针对表5中4种突发事件场景进行求解，求解结果见表6。由表6可知，不同的突发事件场景对列车运行影响不同；并随着突发事件影响程度增加，模型最优解的列车到发时刻总偏差和停运列车数量在增加；对比突发事件场景1、2的调整后列车运行计划可知：由于区间限速影响时空范围较大，会造成严重的大面积列车到发晚点。在本文提出的优化模型和算法下，上述4种突发事件场景均在120 s内求解出最优解，满足列车运行计划调整的实时性要求。

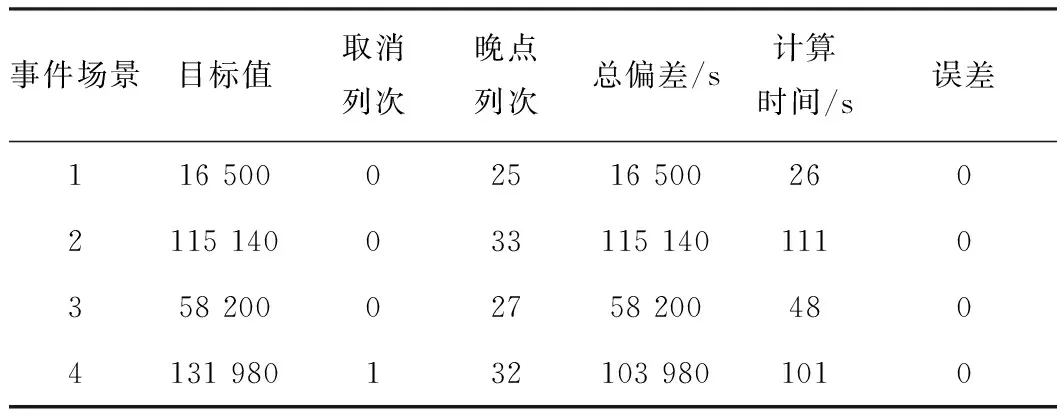
表6 突发事件场景下的计算结果

针对复杂场景4，采用本文所提出的列车实时调度模型进行优化列车实时调度方案。图3和图4分别是列车在途经各站的出发晚点和到达晚点分布情况。从图3和图4可看出，受突发事件影响晚点列车共32趟，其中一部分列车是由于G6132次列车在广州南站始发晚点，造成后续列车发生连带晚点，另一部分是由于乐昌东站至郴州西站区间在08：00—09：00间发生区间临时限速导致。此外，结果表明在列车实时调度下，受影响上行列车晚点在后续车站逐步减少，区间限速对列车运行计划影响较大。

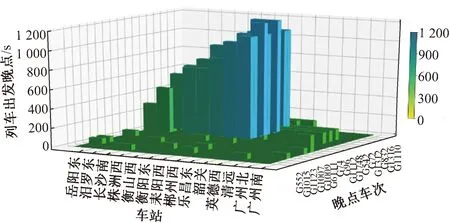
图3 受影响列车在各站出发晚点分布

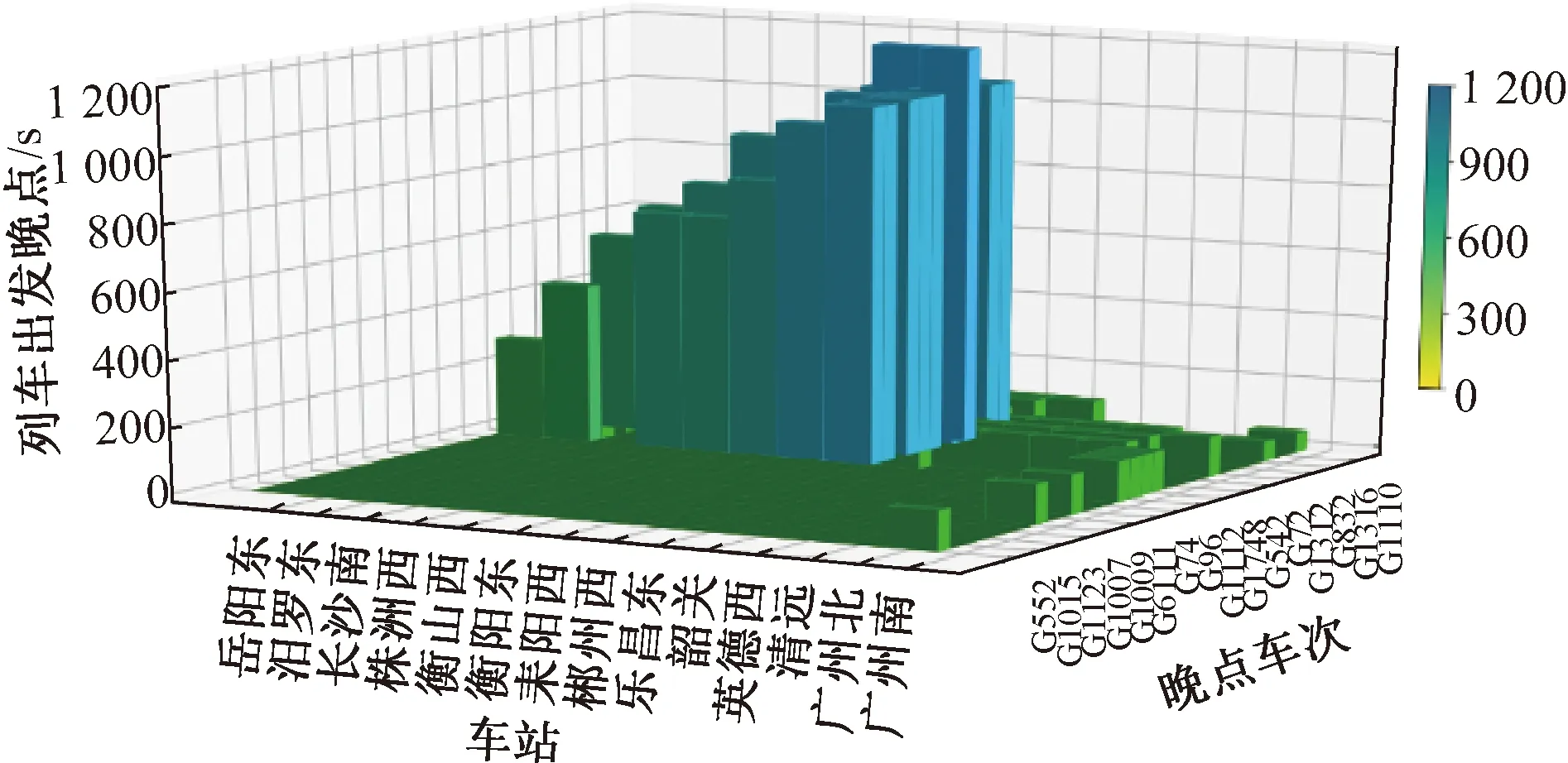
图4 受影响列车在各站到达晚点分布

3.2.2 目标函数权重影响分析

本文所提出模型考虑调整后列车在计划停车站的到发时刻与计划时刻的偏差和取消列车数量的加权费用和最小为目标，为研究两目标费用对列车调度优化模型的影响，以突发事件场景2为例，对模型中目标函数的费用进行影响分析，为模型在实际应用中的费用取值提供参考依据。

设置调整后列车在计划停车站的到发时刻与计划时刻的偏差费用为1，依次增加取消列车策略费用，计算列车优化调度方案的列车总晚点时间和取消列车数量，分析取消列车策略费用的影响，见图5。由图5可见，当调整后列车在计划停车站的到发时刻与计划时刻的偏差费用和取消列车费用相等时，为使得模型目标函数最小，受影响列车全部被取消，列车总晚点为0；随着取消列车策略费用增加，优化后列车调度方案的列车总晚点时间和晚点列车数量逐渐增加，而取消列车数量逐渐减少；当取消列车惩罚增加到550元时，取消列车数量为0，晚点列车数量为33列，列车总晚点达到最大为115 140 s。

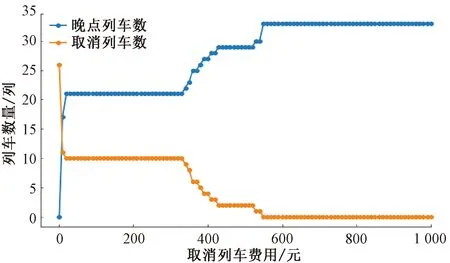
图5 取消列车费用影响分析

考虑临时取消列车对乘客造成负面影响较大，为降低取消列车对乘客的影响，一方面本文模型仅允许在始发站决策是否取消列车，避免取消在途列车；另一方面，调度员可提高临时取消列车费用，减少取消列车数量；此外，为提高列车正点率，可以适当降低取消列车费用，增加取消列车数量，从而降低晚点列车数量。

3.2.3 对比分析

以复杂场景4为例，分别采用所提出模型求解的列车最优运行顺序和以先到先服务的现场调度策略，对调整后的列车调度方案进行具体分析，进一步说明本文提出的模型和算法的有效性。

基于模型最优运行顺序策略和基于先到先服务策略下的模型目标函数上下界收敛曲线见图6。由图6可知，在不同运行顺序策略下，面向铁路实际案例，算法均能在120 s内实现收敛，获取到最优解，满足调度现场列车运行调整方案生成的实时性要求。在本文所提出模型的最优列车运行顺序策略下，所获得的列车实时调度方案明显优于现场按照先到先服务调度策略下的列车调度方案。与先到先服务调度策略相比，基于模型优化下的调整后列车调度方案加权总偏离程度减少25%。由此可见，所提出的模型能够在保证列车安全运行前提下，能够较大的减少突发事件对计划列车运行的影响。

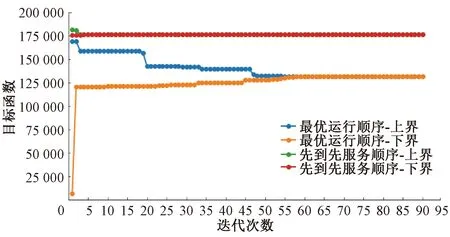
图6 不同策略下目标函数上下界收敛曲线

针对严重突发事件场景4，基于本文所构建模型获得的调度策略，获得调整后列车调度方案见图7。从图7可见，在突发事件场景3的影响下，基于本文所提出模型获得的调度策略，在G2056次列车11：17到达岳阳东终到站时，所有列车恢复按原计划运行图行车，其事件恢复时间为137 min；在相同突发事件场景下，相较于基于先到先服务顺序策略(事件恢复时刻为11：46)，本文所获得最优调整列车调度方案使得突发事件影响恢复时间减少29 min。

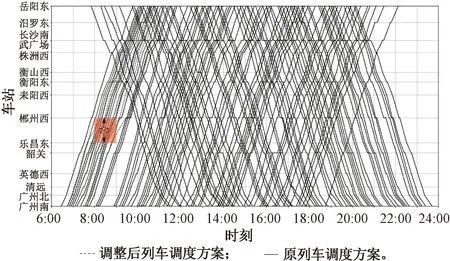
图7 调整后列车调度方案

4 结论

本文通过事件活动网络从宏观层面刻画列车群运行逻辑关系，对严重初始延误和区间限速情况下的列车实时调度问题进行了建模与求解。刻画了列车取消、初始延误与区间限速等相关约束，并对列车晚点、取消等非线性约束进行线性化，以调整后列车调度方案与原列车运行计划的偏离程度最小为优化目标，构建了面向严重初始延误与区间限速的列车实时调度模型；同时，采用了基于分枝定界的列车调度优化算法，能够在线生成列车调度方案。

以武广高速铁路为实际验证算例，设计了4种严重突发事件场景，对所提出的模型和算法进行了实例验证。对模型目标函数费用权重取值进行了分析，给出在实际应用中的一些指导性分析和说明；通过与先到先服务调度策略下的列车调度方案对比，所提出模型和算法能够有效的降低调整后列车调度方案和列车原运行计划的偏离程度(下降25%)和突发事件的恢复时间(减少29 min)。

目前本文主要针对严重突发事件影响初始延误和区间限速情况，在宏观层面对列车运行计划进行调整，但未考虑动车组运用计划和乘务组计划的约束；另一方面，也并未在微观层面对突发事件影响进行分析，如在区间限速情况时，未考虑列车在途降速情况，而这需从微观层面考虑列车的速度牵引曲线，本文为实现解决大规模列车运行计划调整实际案例，对上述细节暂未做详细研究；此外，随着微观层面建模和问题规模的扩大，在权衡求解质量和效率前提下，如何设计更为有效的启发式算法，也是下一步研究方向。