基于高斯扩散模型的爆破粉尘可量化可视化研究
郭 尧
(1.中国矿业大学(北京) 力学与建筑工程学院, 北京 100083;2.海南省发展和改革委员会,海南 海口 570204)
爆破是铁道工程中最基础、最广泛应用的技术之一,特别是随着我国铁路路网结构的基本建成,后续铁路建设越来越多的面临紧邻既有线施工,爆破技术运用好坏直接关系到列车行车安全[1-2]。爆破过程除产生飞石和振动外,现阶段也越来越关注爆破粉尘对列车行车安全的影响,粉尘不但阻断接触网的导电性,还遮挡驾驶员的视线。
目前国内在爆破粉尘防控方面已做了一些研究,但如何形成量化的可复制的防控方法研究较少[3-9]。已有研究主要为爆破烟尘运动阶段划分和各阶段受力特征分析方面,没有很好地与具体水雾降尘技术衔接,因此并未解决工程实际应用中各相关参数的设计问题,这影响了相关方法的深入研究和推广应用。
高斯扩散模型具有较好的处理模糊性和随机性的能力,是研究定性概念和定量数值转换的数学模型[10-16]。为了解决上述问题,考虑爆破粉尘扩散的模糊性和随机性,本文引入高斯扩散模型和Ansys Fluent软件进行模拟计算。首先建立粉尘扩散的物理数学模型,然后采用Matlab和Ansys Fluent软件模拟爆破粉尘扩散规律,得出爆破产尘量和爆破粉尘扩散范围,给出爆破水雾降尘中水袋参数设置,最后以实例表明该方法的可行性和有效性。
1 爆破粉尘扩散模型建立及求解
1.1 模型假设
(1)爆破粉尘源属于在一定爆破区域内,由地面固定位置连续排出的源。
(2)岩石爆炸及粉尘扩散过程时间短暂,爆区周围气象条件保持稳定。
(3)地表对粉尘无吸收和吸附作用。
1.2 模型建立
以爆区中心为原点,设水平下风方向为x轴,水平面垂直下风方向为y轴,垂直水平面方向为z轴,考虑浓度在y方向和z方向对称并符合正态分布,可得浓度q分布为
(1)
式中:A(x)为点源排放强度函数;σy、σz分别为y、z方向的大气扩散参数。
根据质量守恒定理,粉尘排放量应为下风方向所有粉尘的总和,即

(2)

将式(1)代入式(2),可得无界情形下连续点源高斯扩散式为
(3)
爆源为一个区域,具有一定面积,可将式(3)沿x和y方向积分。同时,考虑地面这个界面的存在,浓度测试仪器架设于近地面,即z=0,可得
(4)
式中:QA为爆破粉尘面源排放量,kg/(m2·s);a为爆破区域垂直于下风方向的长度,m;H为爆破源离地高度,m。
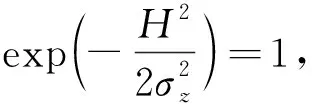
(5)
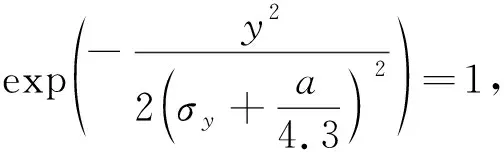
(6)
式(6)中x增大,则σy、σz随之增大,即浓度q随着距离x增大而减小,最大浓度qmax出现在x=0爆心处。
在一次爆破中,布置k个粉尘浓度测点,则粉尘面源排放量取算术平均值,即
(7)
爆破后经过时间t0,爆破粉尘源排放量Q为
Q=QA·t0·a·β
(8)
式中:t0为粉尘量采集时长,s;β为爆破区域平行于下风方向的长度,m。
根据爆破粉尘源排放量计算爆破粉尘排放强度W,可得
W=Q/T
(9)
式中:T为爆破总炸药量,t。
1.3 模型求解
1.3.1 试验方案
考虑爆破粉尘扩散主要受自然风影响,在距离爆破区域中心30 m,下风口25 m处安置Fluke 923型风速测量仪,对爆破现场当时风速进行测量。同时,为便于更近距离、更完整地拍摄,在风速测量仪上方10 m处架设EOS 70D相机,设置相机模式为高频,对粉尘扩散全过程进行记录。粉尘浓度采用FCC-25型防爆粉尘采样仪进行测试,设置采样时间为30 min,采样空气流量为20 L/min,每2 min采集样本一次。三台仪器按线性布置,从爆区下风口20 m处开始,每隔5 m布设一台,现场仪器布置具体见图1。

图1 现场仪器布置示意(单位:m)
1.3.2 试验结果分析
通过逐帧分析数码相机记录的爆破试验全过程,将露天深孔岩石爆破的粉尘扩散根据粉尘形状、持续时间、扩散速度等特征分为三个阶段:启蒙阶段、舒展阶段、扩展阶段。同时,将采集的粉尘样本称重并数据处理后,得到粉尘浓度随时间的变化,见表1。
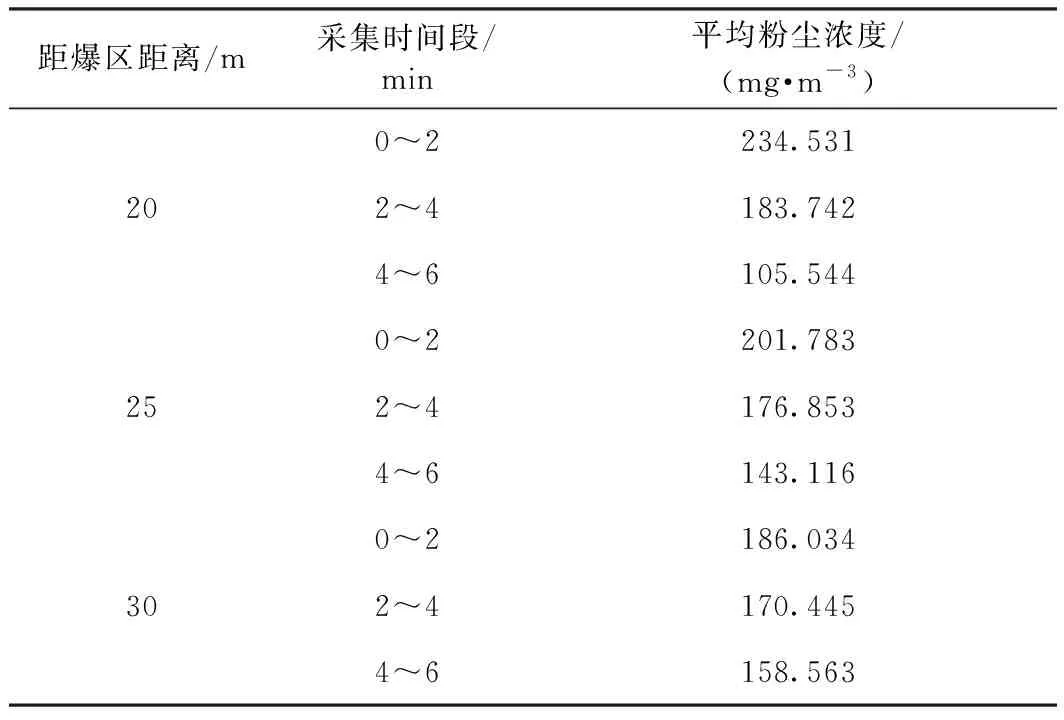
表1 粉尘浓度随时间变化
从表1中可以看出:①粉尘浓度最大值出现在爆破近期,随着时间的推移,粉尘浓度逐渐降低,且距离爆区越近,粉尘浓度的下降速率越快。②由于爆破粉尘主要在爆区内产生,同一时刻,距离爆区越近粉尘浓度越高。③粉尘扩散主要受爆破产生的高温高压气体膨胀所致,距离爆区越远,爆破气体与温度压力以及大气压力更易形成平衡,粉尘扩散速率减慢。
1.3.3 计算结果分析
2021年5月22日16时,在北京郊区进行爆破试验,当时天空晴朗,风速为1 m/s,爆区长度为40 m、宽度为13.5 m,一次爆破总药量为5.04 t,依据式(8)、式(9)计算得出:Q=716.56 kg、W=142.17 kg/t
同时,根据粉尘排放量,利用式(6),计算得出不同距离的粉尘浓度关系,见图2。

图2 粉尘浓度随x方向的变化规律
由图2分析可得,粉尘浓度q随着距离x增大而减小,当x<30 m时粉尘浓度大且急剧下降,当x>30 m粉尘浓度趋于缓和,因此水袋应在爆破区域外30 m范围内铺设效果最佳。
依据式(5),将爆破区域宽度y考虑进去,得到z=0时,粉尘浓度q随x、y的变化,见图3。
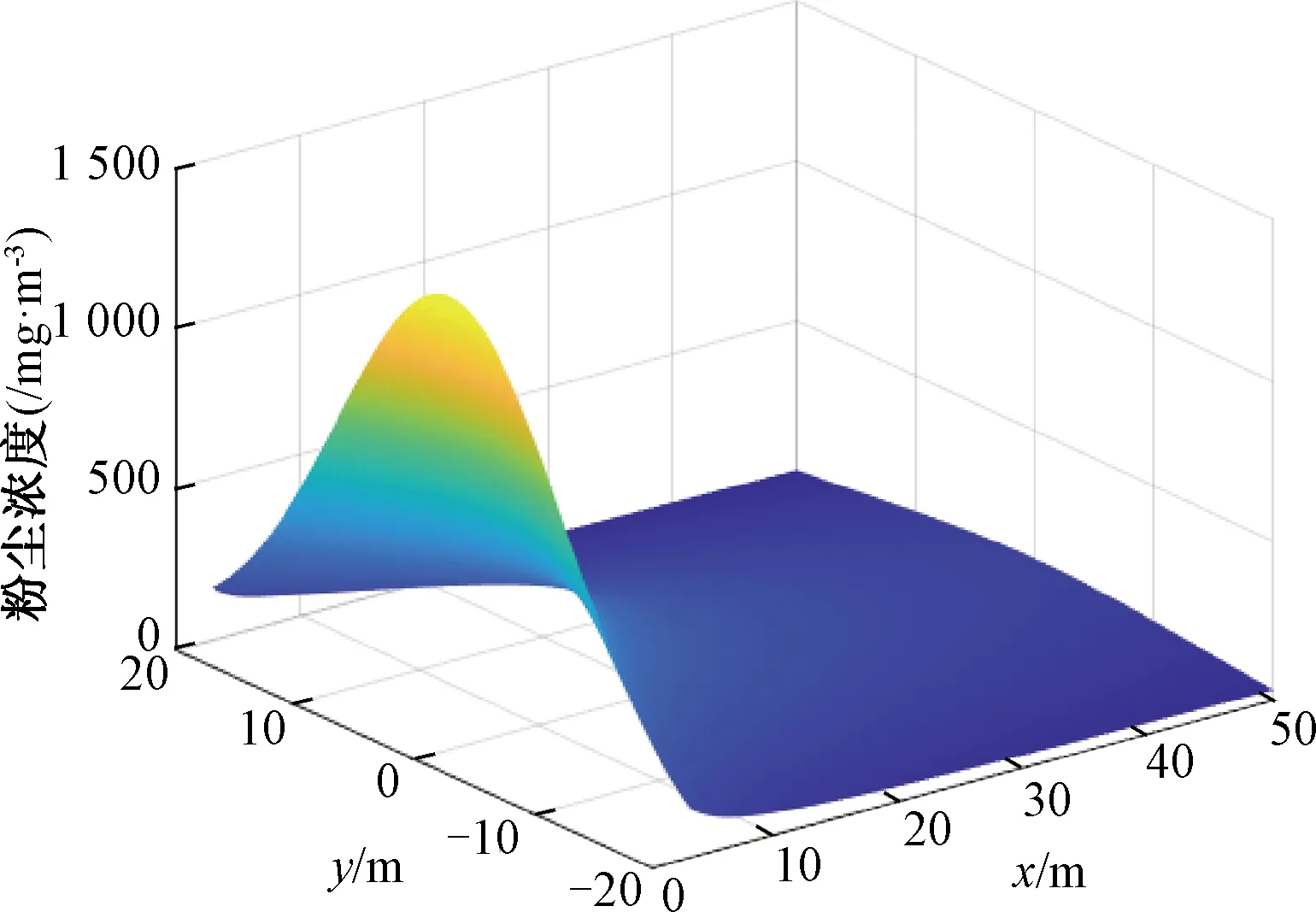
图3 粉尘浓度随x、y方向距离的变化规律
从图3中分析得出,粉尘浓度q随着爆心距离y增大而减小,且基本符合对称分布。当y<20 m时粉尘浓度大且急剧下降,当y>20 m粉尘浓度小也趋于缓和。可以看出爆破粉尘浓度最大值出现在爆心处,而爆破区域边缘的粉尘浓度已经很小,因此设计水袋长度以不大于爆破区域宽度为宜。
利用式(3)对不同高度z的粉尘浓度分布规律进行计算,如图4所示。
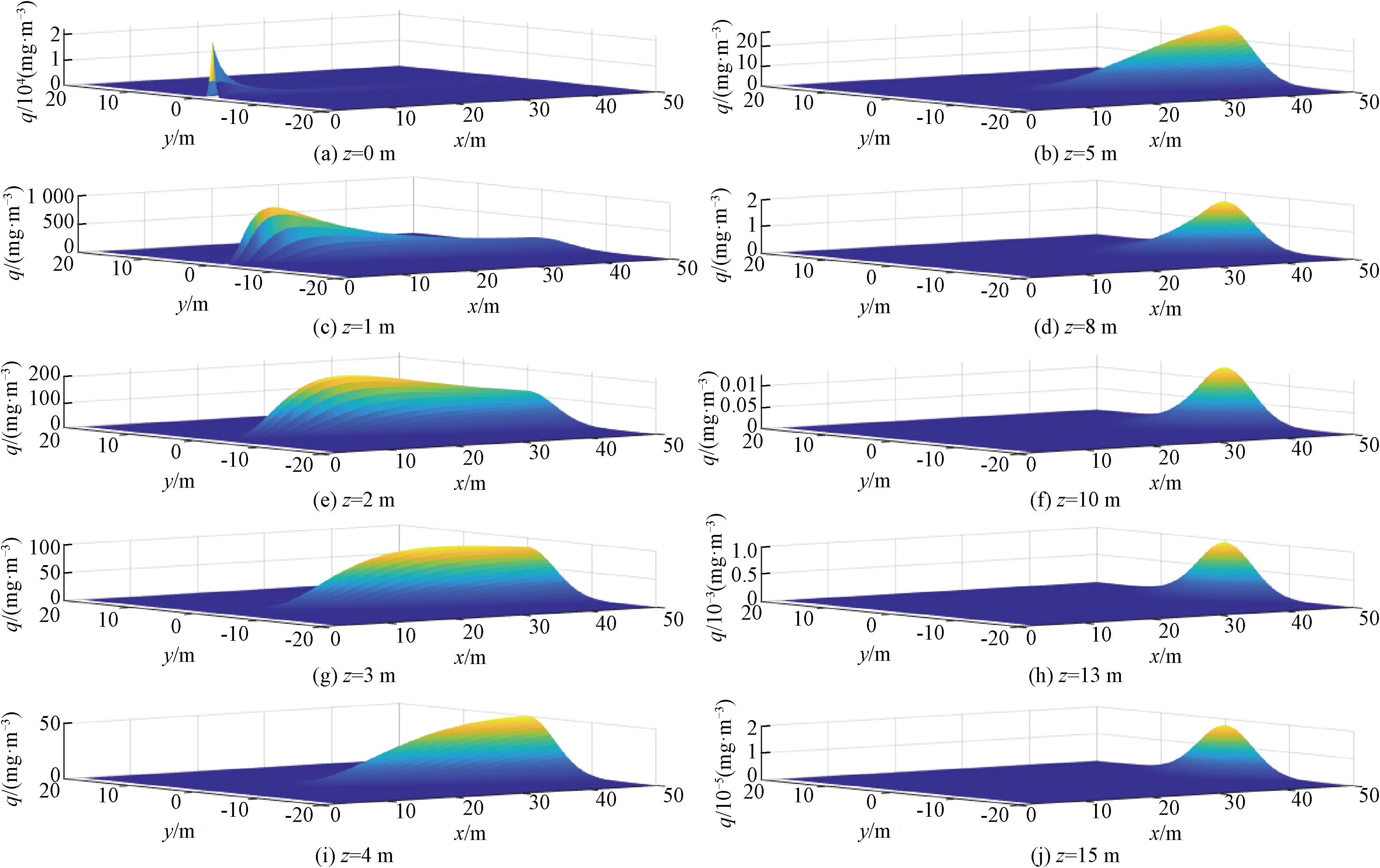
图4 粉尘浓度随x、y、z三向距离的变化规律
从图4中分析得出,粉尘浓度q随着高度z的增大而减小,当z<2 m时粉尘浓度由爆生气体所携带粉尘量决定,当z>2 m粉尘浓度主要受大气扩散因素影响,爆破近区粉尘浓度逐渐小于爆破中远区,当z>13 m粉尘浓度趋于零。因此,水袋炸高设计时,只要水雾高度大于13 m,就可以实现水雾对爆炸产生粉尘的全覆盖。
2 数值模拟及结果分析
根据现场露天台阶爆破试验模型的布置和尺寸,使用Soildworks建立三维几何模型,如图5所示。其中,台阶倾角为75°,梯段高度为12 m,底盘抵抗线为3.8 m,炮孔间距为4.5 m,炮孔排距为3.8 m,炮孔孔深13.5 m,超深1.5 m。

图5 路堑爆破三维几何模型(单位:m)
边界条件和求解过程相关参数见表2。

表2 边界条件及求解参数设置
为了分析爆破粉尘浓度随时间的变化规律,在数值模拟过程中设置监测点和线,以分析不同位置处粉尘浓度随时间的变化规律,如图6所示。

图6 监测点和监测线位置图(单位:m)
其中沿着x方向等间距共设置7个监测点:1(5 m,5 m,0),2(10 m,5 m,0),…,7(35 m,5 m,0),深孔爆破监测点粉尘浓度随时间变化如图7所示。对露天台阶附近的浓度时空分布特征进行分析,以点2为基点,分别在x,y,z方向设置line1、line2、line3三条监测线,如图8所示。

图7 监测点粉尘浓度随时间的变化过程
沿监测点的x轴方向,各点粉尘浓度随着时间的推移,总体呈先急剧上升至峰值,后缓慢下降的分布趋势,监测点离深孔爆破区域的距离越远,粉尘浓度峰值越低且达到峰值所需的时间越晚。如图7所示,点1~7分别在55、55、55、70、60、70、60 s时粉尘浓度到达峰值0.031 2、0.015 1、0.012 6、0.009 2、0.004 9、0.002 8、0.001 5 kg/m3。同时,可以看出点6 由于位于30 m以外粉尘浓度基本保持不变且数值微小。
由图8可知:
(1)沿监测线line1,如图8(a)所示,在台阶起爆瞬间粉尘浓度达到最大,并随着距离的增加整体呈逐步降低的分布趋势;而对于同一检测点,随着时间推移,其粉尘浓度先增大后逐步下降。
(2)沿监测线line2方向,如图8(b)所示,由于监测线与露天台阶爆破区域存在一定距离,故随着时间的推移,粉尘浓度在z轴方向整体呈现先上升后减少的变化规律,且在爆破后30~60 s内达到峰值;在监测点z=0两侧等间距的其他监测点,随着时间和距离的增加呈现大致对称分布的态势;当大于爆区宽度时,粉尘浓度已降至最大粉尘浓度的25%以下。
(3)沿监测线line3方向,如图8(c)所示,不同时刻下的粉尘浓度均随着高度的增加呈现先增大后减小的趋势,这是由于爆破过程中的粉尘沿着垂直爆破面方向扩散;在高度小于2.5 m时,粉尘呈现逐步上升至峰值的趋势;随着高度的持续上升,绝大多数的粉尘颗粒难以继续克服重力作用继续向上扩散,故呈下降的趋势,并在13.75 m附近基本趋于稳定。

图8 监测线粉尘浓度随时间的变化过程
3 实例验证
3.1 试验概况
试验选择在海南昌江石灰岩矿区进行,岩石硬度适中。首先,在爆区抛掷方向布设两排水袋,水袋与自由面的距离按不超过30 m布设,分别设为15、25 m;水袋长度按爆区一半宽度30 m布设;每个水袋炸高按15 m左右控制,使用3根导爆索引爆,起爆时间分别滞后第一排孔1、1.5 s起爆。其次,在自由面前方80 m处布设两台测尘仪。最后,在距自由面50、100、150 m处布置集尘盒检测单位面积落尘量。现场试验布置和效果见图9、图10。

图9 试验方案示意图(单位:m)

图10 粉尘和爆炸水雾的作用过程
3.2 试验结果及分析
通过图10可以看出,在有水袋布设的方位,由于采用了水雾捕获粉尘的措施,爆破粉尘浓度明显小于没有采用任何降尘措施的一侧。
对落尘盒和测尘仪采集的结果进行数据处理分析,见表3、表4。

表3 落尘量统计值

表4 不同措施下粉尘浓度
从表3可以看出,在采用水雾降尘措施和未采用降尘措施后方50、100、150 m处,粉尘量分别增加31%、增加22%和减少27%。说明有水雾的情况下,水雾捕获尘粒作用明显,加速了尘粒的沉降,在近区大部分粉尘就已降落,远区受爆破产尘总量影响落尘量减小。
从表4数据分析可知,爆后50 s,在采用水雾降尘措施后方粉尘浓度比未采用降尘措施减少了27.2%,降尘效果明显。
4 结论
在研究爆破产尘理论的基础上,本文将高斯扩散模型引入到爆破粉尘扩散规律认识中,利用Matlab和Ansys Fluent软件对粉尘扩散进行了数值模拟,并用实例进行测试和验证,得出以下结论:
(1)基于高斯扩散模型,计算得出此次爆破产尘总量为716.56 kg,爆破粉尘排放强度为142.17 kg/t。
(2)基本认清爆破粉尘扩散规律:①从下风方向看,粉尘浓度随着距离增大而减小,当粉尘距离自由面30 m以远后,粉尘浓度变化趋于缓和且数值很小;②从爆区宽度看,粉尘浓度随着距爆区中心距离增加而呈现大致对称分布的态势,当大于爆区宽度时,粉尘浓度已降至最大粉尘浓度的25%以下;③从爆破粉尘高度看,粉尘浓度均随着高度的增加呈现先增大后减小的趋势,随着高度上升至13.5 m左右,粉尘浓度基本趋于稳定且微小。
(3)自由面前水袋设置参数基本确定,水袋设置距离自由面不超过30 m,水袋长度不超过爆区宽度,水袋炸高13.5 m为益。
(4)最后通过实例验证了基于以上参数设置,爆破水雾降尘技术的可行性和有效性,降尘效果达到27.2%。
本方法从粉尘扩散模糊性和随机性的角度出发,客观科学地模拟计算了粉尘扩散规律和扩散范围,为现场采用水雾降尘施工提供了可复制、可推广的方法。

