基于变分自编码器的MVB网络异常检测方法

杨岳毅，王立德，陈 煌，王 冲

(北京交通大学 电气工程学院, 北京 100044)

多功能车辆总线(Multiple Vehicle Bus，MVB)是一种基于串行数据通信总线的通信网络，广泛应用于高速动车组和地铁列车[1]。MVB连接中央控制单元、网关、远程IO模块RIOM等车载列车网络控制设备，传输牵引制动控制指令、列车运行状态等重要信息[2]。由于恶劣的工作环境，许多因素都可能造成MVB网络通信性能退化，严重时造成通信故障，危及列车运行安全[3]。目前，MVB网络检修仍处于故障检修模式，依赖于专家经验进行故障排查，无法有效监测网络状态，不能及时发现网络异常。因此，有效的MVB网络异常检测方法对于保障列车运行安全和降低运维成本具有重要意义。

传统总线型网络的异常检测多通过监测数据链路层信息来实现。文献[4]选用CAN总线消息接收延迟时间来反映消息响应时间的变化，提出一种基于巴氏距离的故障检测方法。文献[5]提出一种基于自适应神经模糊推理系统的故障诊断方法，根据一定时间窗口内总线错误帧数评估网络健康状态。文献[6]设计了一种MVB协议分析装置，能够对MVB过程数据、消息数据等进行实时获取和解析，为检修维护提供了必备工具。文献[7]提出一种基于贝叶斯规则后验概率模型的MVB误码率估计算法，能够用于测试MVB通信质量。然而，对于因线缆性能退化、连接器老化等引起的MVB网络异常，由于其主要造成信号物理波形畸变，且通常在列车运行时才会出现丢包率、误码率等链路层指标大幅升高的现象，因此传统方法无法实现有效的异常检测。

总线型网络的物理层包含大量网络状态和故障信息，可用于网络状态监测和异常检测。文献[8]提出一种基于动态集成学习的城轨列车制动系统CAN总线异常检测方法，提取稳态幅值、超调、位时间等9种CAN总线信号物理波形特征用于模型训练。文献[9]从CAN总线信号物理波形中提取17种时域和频域特征，采用3种经典机器学习算法实现入侵检测。文献[10]提取MVB网络信号物理波形一致性特征，采用多核学习支持向量机进行端接故障诊断。文献[11]提取6种MVB网络信号物理波形特征，提出一种基于支持向量描述的MVB网络健康评估方法。然而，这些方法通常依赖专家经验选择和提取信号物理波形特征，在缺乏先验知识的情况下存在检测准确率不高、效率低等问题，只适用于特定应用场景。

实际中，由于缺乏大量标记的异常数据，造成正常数据和异常数据的严重不平衡，因此相比于监督学习，无监督学习和半监督学习更适用于异常检测领域[12]。变分自编码器(Variational Autoencoder，VAE)是一种无监督的深度生成模型，由于其比自编码器(Autoencoder，AE)具有更好的泛化能力，近年来已经成功应用于异常检测领域[13]。VAE通过训练学习到正常数据集的概率分布，将偏离这个概率模型的数据检测为异常数据[14]。其中，阈值选择对基于VAE的异常检测方法十分重要。文献[15]通过采用交叉验证的方法进行阈值选择，但需要足够的验证数据集。文献[16]通过测试集对模型进行评估，选择最佳模型对应的阈值，但其泛化能力较差。

本文提出一种基于VAE的MVB网络异常检测方法，无需人工特征提取，直接将MVB网络原始信号物理波形作为模型输入，采用重构误差作为异常检测判断依据。模型训练采用半监督学习方式，训练阶段只需要正常数据集，并利用核密度估计(Kernel Density Estimation，KDE)设置异常检测阈值。在实验室环境搭建MVB网络实验平台，验证本文所提方法的有效性。

1 MVB网络异常

MVB网络采用非归零差分曼彻斯特编码，波特率为1.5 Mbps。实际应用中，MVB网络通常选用电气短距离和电气中距离2种传输介质，采用RS-485传输物理层差分电信号，通信线缆规定为截面积0.34 mm2(AWG22)～0.56 mm2(AWG20)的屏蔽双绞线[17]。MVB网络双绞线等效回路见图1。

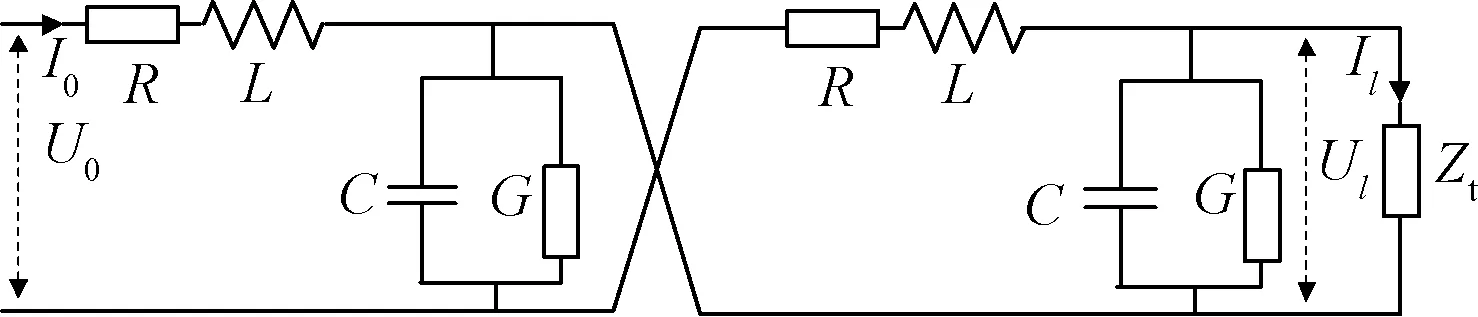
图1 MVB网络双绞线等效回路

图1中R、L、C、G分别为单位长度线缆回路的有效电阻、电感、电容、电导。当等效回路中施加正弦波电压、电流时，设初始端的电压和电流分别为U0和I0，线缆长度为l，可以得到线缆l处的电压Ul和电流Il为

(1)

式中：Zc为特征阻抗；λ为传播参数。

由式(1)可知，线缆l处的电压和电流由入射电压或电流(-λl)和反射电压或电流(λl)两部分组成，入射电压与输入电流之比和反射电压与反射电流之比都等于特征阻抗Zc。协议规定的MVB特征阻抗Zc为120 Ω。

当终端电阻Zt=Zc时，网络阻抗匹配，双绞线电压信号传递函数F=|Ul/U0|=e-λl，只与传播参数λ、线缆长度l有关，因此可以避免出现反射现象。

当阻抗不匹配时，双绞线电压信号传递函数为

(2)

函数由传播参数λ、线缆长度l、终端电阻Zt和特性阻抗Zc共同决定。阻抗不匹配会引起能耗增加、物理波形畸变，导致MVB网络通信质量下降，严重时引发网络通信故障。

MVB线缆反射系数定义为线缆反射波电压与入射波电压之比，则线缆终端处反射系数Γt为

(3)

由于长时间处于复杂恶劣的工作环境中，多种原因都可能造成MVB网络故障，常见的MVB网络异常有：

(1)断路故障。网络断路故障常发生于通信线缆和设备网卡连接器，造成部分设备离线，同时剩余网络设备因阻抗不匹配而引起严重的信号物理波形畸变。

(2)短路故障。芯片击穿、管脚短接、通信线缆破损等原因会造成MVB网络差分通信线路短路故障，导致网络通信中断。

(3)端接故障。振动或者维护不当等原因会使MVB网络终端电阻缺失或者配置位置不正确，造成网络阻抗不匹配，引起网络信号物理波形畸变，通信性能退化，严重时造成网络通信中断。

(4)传输介质故障。由于MVB网络工作环境复杂恶劣、不合理的检修维护等原因，长时间运行会造成网络线缆、线缆连接器、通信网卡电子元器件等性能退化，造成网络原有特性阻抗发生改变，从而使得网络阻抗不匹配，引起网络信号物理波形畸变，抗干扰能力降低，网络通信性能退化。

(5)电磁干扰。MVB网络长期处于列车复杂电磁环境下，不合理的布线、屏蔽层破损、不正确的接地等原因，都可能干扰网络信号正常传输，引起网络通信故障。

2 异常检测方法

2.1 变分自编码器

变分自编码器VAE是一种有向概率图模型，包括概率编码器和概率解码器，其模型结构见图2。

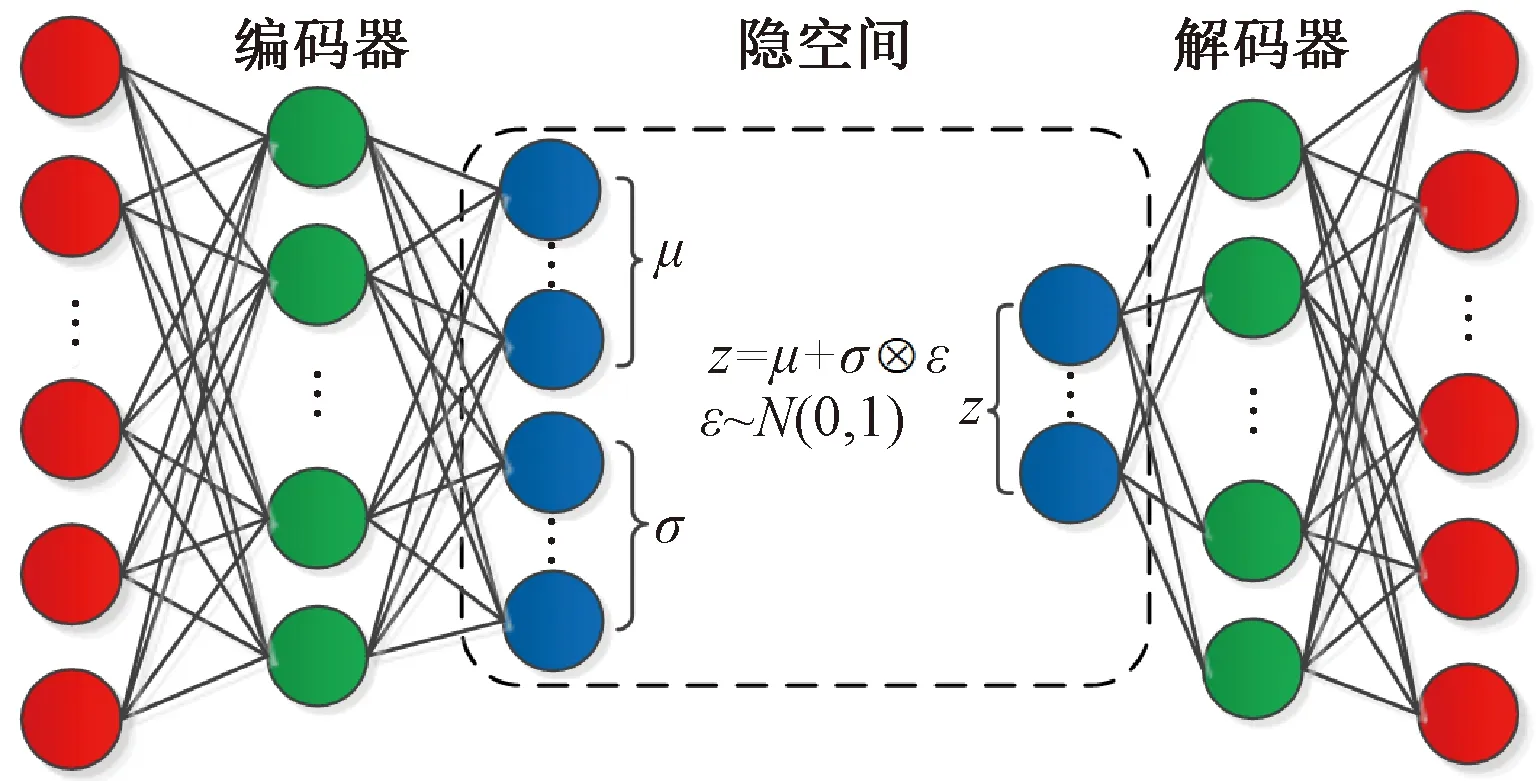
图2 变分自编码器模型结构

由于无法得到准确的真实后验概率pθ(z|x)，因此采用变分推断的方法，通过训练概率编码器得到后验概率qφ(z|x)来近似逼近pθ(z|x)。概率解码器相当于一个生成模型pθ(x|z)，其中z为隐变量。边际似然由单个数据点的边际似然lnpθ(xi)(i=1,2,…,n)的总和得到，n为训练样本数。对单个数据点的边际似然可以表示为

lnpθ(xi)=DKL(qφ(z|xi)‖pθ(z|xi))+

L(θ,φ;xi)≥L(θ,φ;xi)

(4)

式中：DKL为散度，是衡量两个概率分布间差异性的指标，为非负数；L(θ,φ;xi)为数据边际似然的变分下界；φ为变分参数；θ为生成参数。

由于lnpθ(xi)为定值，为了使pθ(x|z)和qφ(z|x)间的散度最小化，需要最大化L(θ,φ;xi)。同时，采用神经网络训练得到变分参数φ和生成参数θ，这也是VAE与AE相关联的地方。

数据xi的边际似然下界L(θ,φ;xi)可表示为

L(θ,φ;xi)=

-DKL(qφ(z|xi)‖pθ(z)+Eqφ(z|x)[lnpθ(xi|z)]

(5)

式中：E为期望。

设一个输入数据x∈Rd，d为样本维度，qφ(z|x) 和pθ(z)服从高斯分布，变分自编码的优化函数LVAE可定义为

LVAE=LMSE(x,xc)+wLKLD(μ,δ)

(6)

LMSE(x,xc)=‖x-xc‖2

(7)

LKLD(μ,δ)=DKL(qφ(z|x)‖pθ(z))=

DKL(N(z;μ,δ2)‖N(z;0,1)=

(8)

式中：LMSE(x,xc)为重构误差优化函数，用于实现模型输出近似重构模型输入；LKLD(μ,σ)为正则化项，用于实现近似后验概率qφ(z|x)逼近先验概率pθ(z)；w为权重超参数；μ、δ分别为qφ(z|x)的平均值、方差；N为正态分布函数。

基于VAE的异常检测方法属于基于重构的方法，假设异常数据是无法有效进行重构的，相比于基于AE的异常检测方法，基于VAE的异常检测方法具有以下优点：

(1)相比于AE的确定性映射关系，VAE是一个随机生成模型，其使用概率编码器构建隐变量分布，在采样过程中考虑隐空间的可变性。当正常数据和异常数据具有相同平均值时，VAE依然可以通过隐空间的方差进行判断。

(2)VAE重构误差不仅考虑输入数据与重构数据之间的差异，同时考虑重构的可变性，可以根据隐变量方差选择性地进行重构。当隐变量方差较大时，VAE能够容忍输入数据和重构数据之间的较大差异，而减小方差较小时的重构概率。

(3)VAE 根据先验概率从隐空间进行多次采样，计算平均重构误差作为重构概率，比AE在异常检测领域具有更高的鲁棒性。

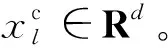
(9)

由式(9)可得异常检测得分向量S={s(x1),s(x2),…，s(xn)}。对于正常数据，训练好的模型能够很好地对其重构，异常检测得分较低；对于异常数据，模型无法正确对其重构，异常检测得分较高。同时，可以将MVB网络节点通信性能的健康指标HI定义为

(10)

(11)

式中：c0为尺度常数[18]；cpre为常数，根据专家经验设定，一般取值范围为[0.90,0.99]。

2.2 阈值设定

对于基于VAE的异常检测方法，阈值选择直接影响模型的检测性能。KDE为一种估计随机变量概率密度函数的非参数方法，无需假设所研究变量的分布函数形式。选择MVB正常数据的异常检测得分作为训练数据，采用KDE估计正常数据异常检测得分的概率密度函数，然后通过累积分布函数(Cumulative Distribution Function，CDF)得到小于等于设定阈值的所有数据的概率分布，并通过显著性水平来平衡模型漏检率和误报率。相比于专家经验的阈值设定方法，该方法更加客观和合理。

设训练集数据的异常检测得分为向量S，通过KDE可以得到其概率密度函数为

(12)

式中：si为第i个训练样本的异常检测得分；K(·)为核函数；h为带宽。

径向基核函数(Radial Basis Functions，RBF)是一种最常用的概率密度估计核函数，其估计训练集的概率密度函数可表示为

(13)

带宽h对KDE的性能影响很大，本文选择文献[19]提出的一种选择准则：

(14)

采用KDE得到训练集异常检测得分的概率密度函数后，CDF可以表示为

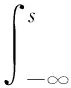
(15)

然后，根据显著性水平α∈[0,1]和CDF，可以设定阈值为sa，满足F(sa)=1-α。在这种情况下，一个数据点的异常检测得分s≥sa时，(1-α)·100%的概率为异常点。α值越大表示越低的漏检率，表明模型将异常数据误判为正常数据的概率越小；α值越小表示越低的误报率，表明模型将正常数据误判为异常数据的概率越小。因此，为了平衡模型的误报率和漏检率，在异常检测应用领域中推荐设置α值为0.1。

2.3 检测流程

基于VAE的异常检测方法流程见图3，主要包括以下部分：

Step1数据预处理。将MVB信号物理波形数据进行归一化处理；然后，将数据集划分为训练集和测试集，其中训练集只有正常数据，测试集包括正常数据和异常数据。

Step2离线训练阶段。将训练集X输入VAE进行训练，得到正常数据异常检测得分向量S∈Rn×d。

Step3阈值设定。由KDE得到训练集异常检测得分s的概率密度函数p(s)，根据得到的CDF和显著性水平α来设定阈值st。

Step4在线测试阶段。将测试集的一个样本Xnew输入训练好的VAE模型，得到其异常检测得分snew，如果snew≥st则判为异常样本，反之为正常样本。

Step5为了防止因噪声干扰引起过多误告警，在实际应用时可增加一个计数器，设定一个告警阈值f。当在设定的时间窗口内检测到的网络异常数大于f时，MVB网络协议分析仪告警，提示需要对网络进行检修维护。

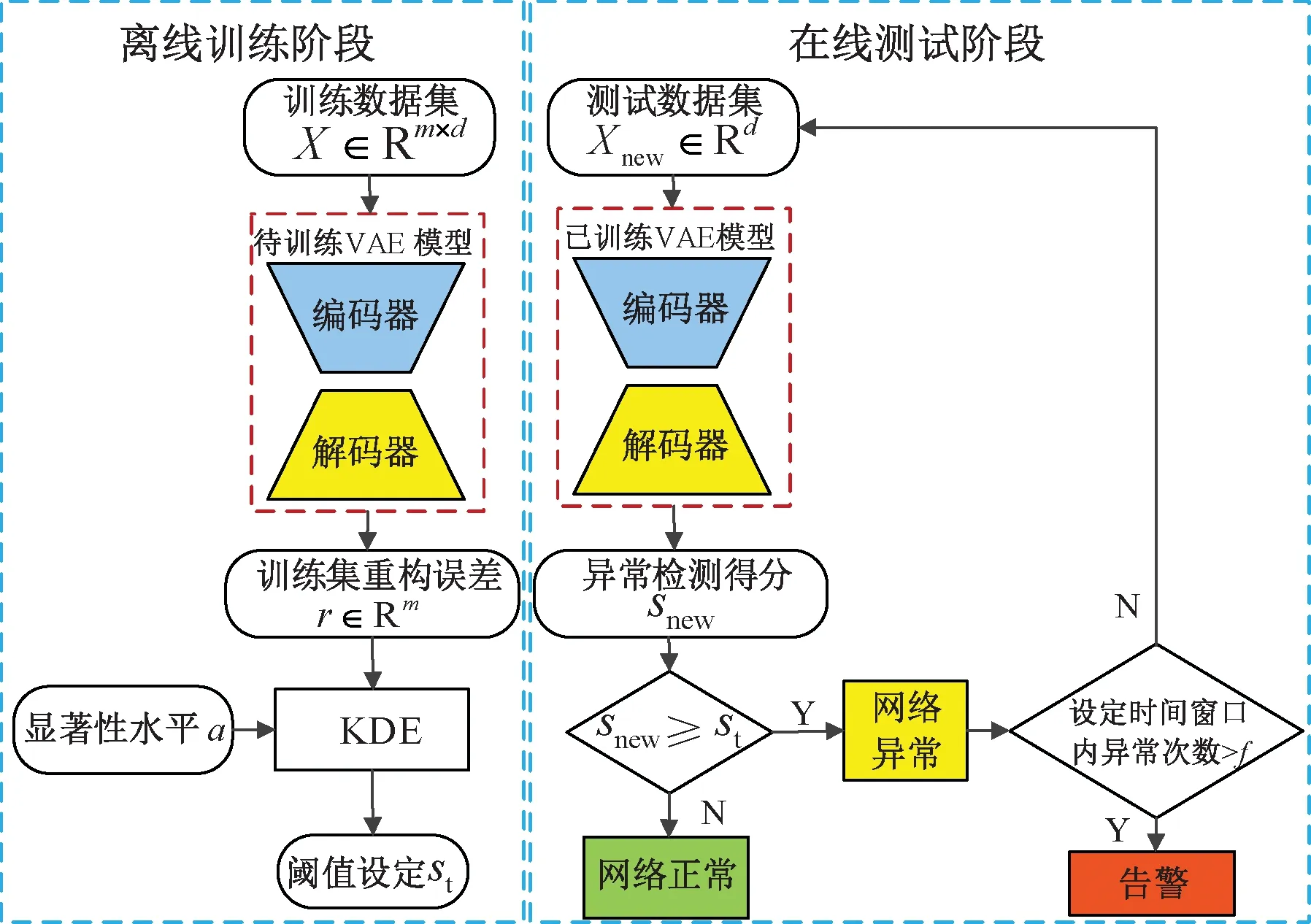
图3 异常检测方法流程

3 实验验证

在实验室环境下搭建MVB网络实验平台，包括列车逻辑控制单元LCU、UIC网关、Duagon D113网卡、自主研制的故障注入板卡、自制MVB通信板、自主研制的MVB协议分析仪等设备。

在实际应用中，MVB网络线缆长度l和传输参数λ通常保持不变，由式(2)可知，MVB网络故障的类型和严重程度主要由终端电阻Zt和特性阻抗Zc共同决定。在MVB网络实验平台上，通过自制故障注入板卡进行故障模拟。故障注入示意见图4。模拟故障类型包括：断路故障(Fault1)、去掉一个终端电阻模拟的端接故障(Fault2)、并联电阻模拟的传输介质故障(Fault3)、串联电阻模拟的传输介质故障(Fault4)、短路故障(Fault5)。当发生短路或断路故障时，特性阻抗Zc或终端电阻Zt为零，Γt=1或-1，MVB网络发生信号全反射，发射波被完全反射，波形畸变严重。当发生端接、连接器老化以及传输线缆性能退化等故障时，0<Γt<1，MVB网络发生部分反射，造成网络波形质量下降，无法满足协议规定的一致性要求。

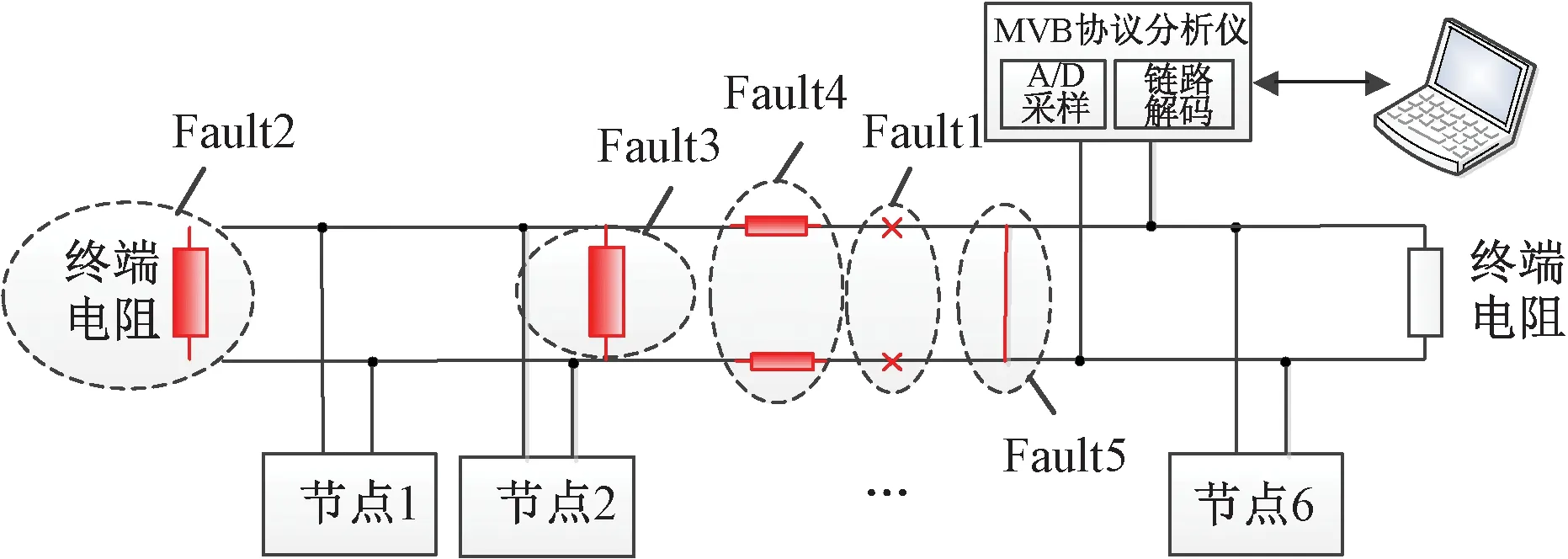
图4 故障注入示意

采用MVB协议分析仪进行信号物理波形数据采集，采样频率为100 MSa/s，主要数据描述见表1。由于短路故障(Fault5)导致信号物理波形严重畸变，无法准确识别数据发送节点，因此数据来源不区分具体节点。将5 000个正常数据构成训练数据集，将从所有节点得到的5 000个正常数据和所有故障类型得到的5 000个故障数据构成测试数据集。

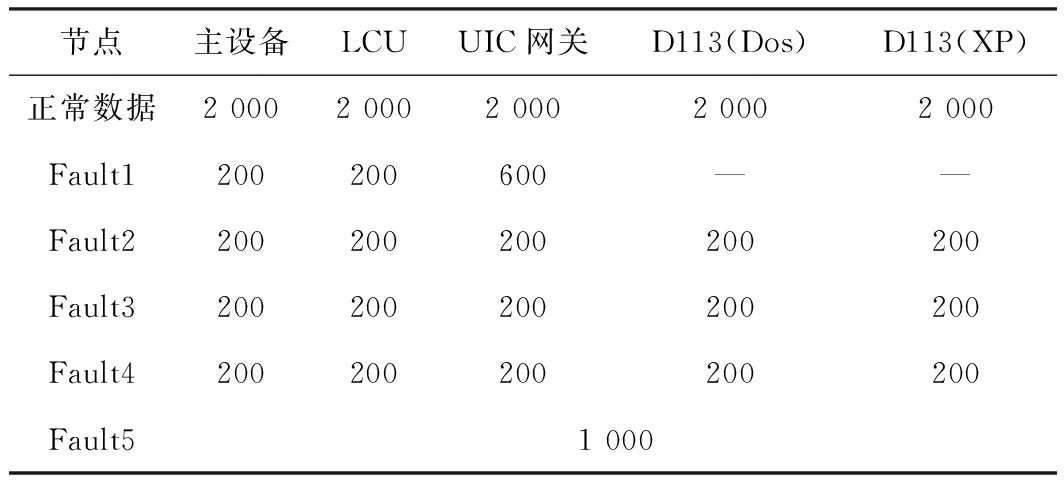
表1 主要数据描述 个

考虑MVB数据帧的起止分界符不因数据不同而改变，本文选取MVB信号物理波形数据前800个采样点作为VAE模型输入，VAE网络结构为800-512-256-10-256-512-800，AE具有相同网络结构。VAE和AE均采用Adam优化器，学习率在[0.001,0.01,0.05,0.1]中选择，batch_size=100，epochs=500。输出层神经元激活函数为Sigmoid，其他层神经元激活函数选择ReLu。所有算法实验运行于配置为Intel 5 2.8 GHz 双核CPU、16 GB 内存的电脑，系统为Ubuntu V18.04.2，编程语言采用Python3.6。

3.1 实验结果可视化

为了直观展示VAE的异常检测性能，采用t-分布邻域嵌入算法(t-distributed stochastic neighbor embedding，t-SNE)将VAE隐变量降至二维。测试集二维隐变量分布见图5。

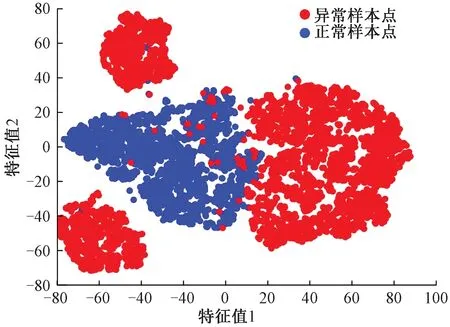
图5 测试集二维隐变量分布

由图5可知，训练好的VAE模型已经基本将正常数据和异常数据的隐变量进行了分离，更易被解码器进行识别。

采用t-SNE将测试集的隐变量降至二维后，绘制每一维的KDE曲线二维隐变量KDE曲线见图6。由图6可看出，每一维度的正常数据的隐空间与异常数据的隐空间均只有很少的重叠，表明VAE具有很强的识别正常数据和异常数据的能力。

3.2 网络状态评估

不同网络状态下的异常检测得分见图7。网络断路、短路故障的故障现象较为明显，信号物理波形严重畸变，异常检测得分较高。网络端接故障和传输介质故障的故障现象不明显，信号物理波形畸变较轻微，其异常检测得分与正常数据的较为接近。实验结果表明，VAE已经很好地学习到正常数据的内部模式，定义的异常检测得分能很好地量化异常数据偏离正常数据的程度。

图6 二维隐变量KDE曲线

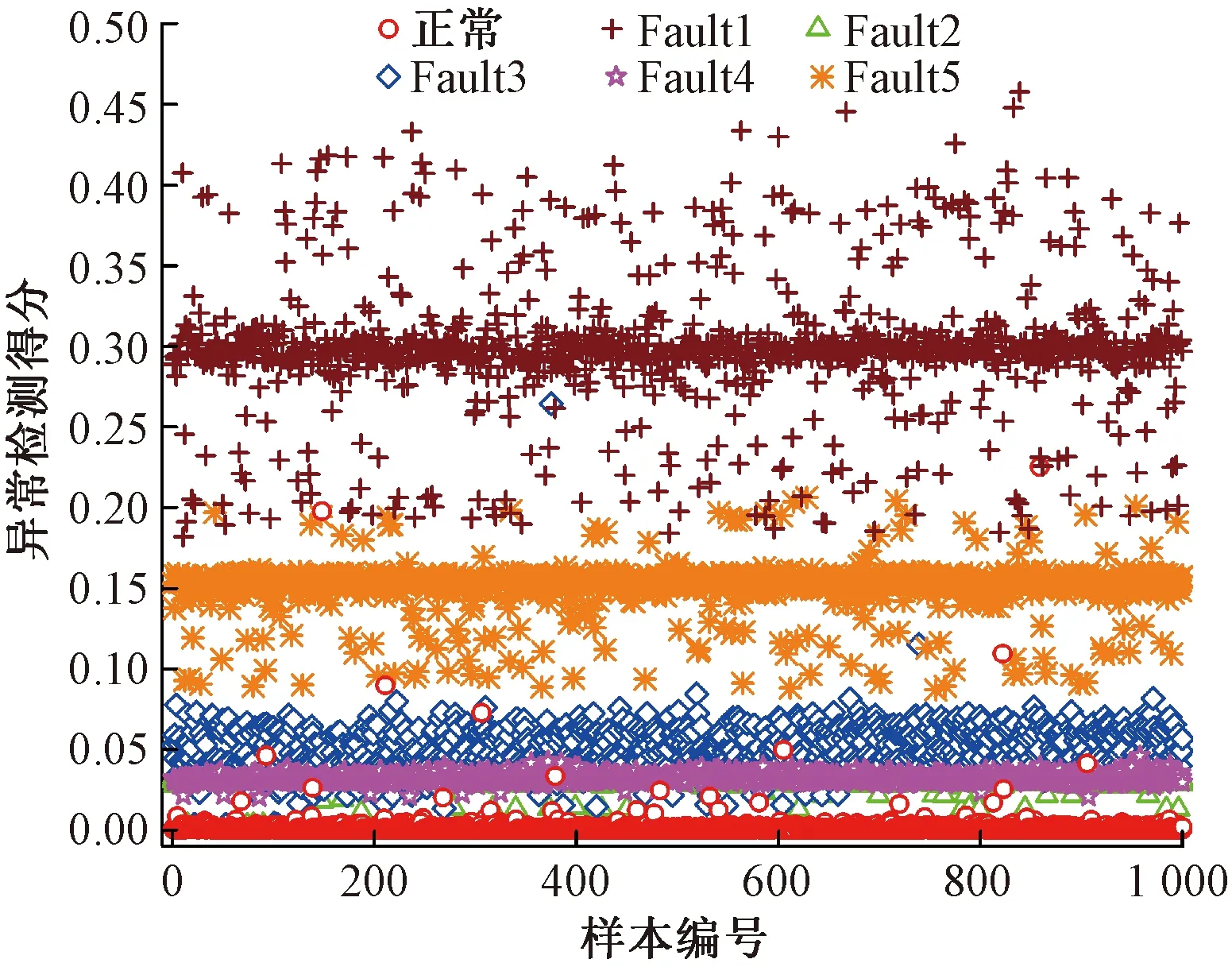
图7 不同网络状态下的异常检测得分

LCU节点不同状态下发送信号物理波形的健康指标见图8。正常状态下的健康指标基本大于90，断路故障和短路故障下的健康指标均低于35。结果表明，本文设计的健康指标能够准确反映节点信号物理波形偏离正常的程度，可以作为MVB网络状态监视和状态检修的依据。

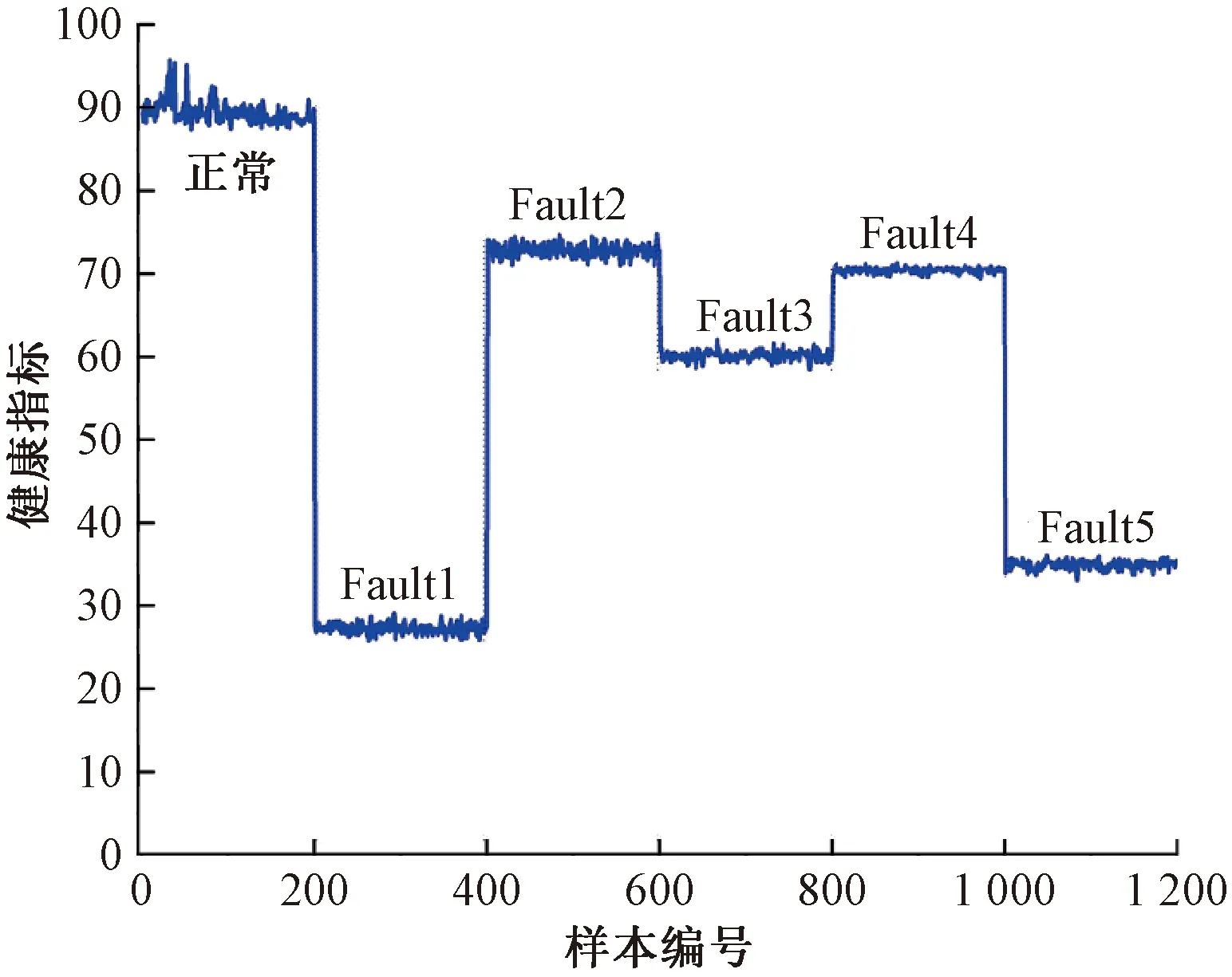
图8 不同状态下LCU节点健康指标

3.3 对比实验

为了验证本文提出方法的优越性，将其与几种经典异常检测方法进行对比实验。局部异常因子算法(Local Outlier Factor，LOF)是一种基于密度的无监督异常检测方法，邻域数从[20,50,100]中选择；孤立森林(Ioslation Forest，iForest )是一种基于集成学习的异常检测方法，决策树数量从[50,100,200]中选择；一分类支持向量机(One-Class Support Vector Machine，OCSVM)是一种基于边界的半监督学习异常检测方法，核函数选择RBF，参数v从[0.01,0.05,0.1,0.2]中选择；基于角度的离群点检测(Angle-based Outlier Detection，ABOD)通过估计一个点到另一个点的差分向量夹角的方差来进行异常检测，无需任何参数选择。

本文选择AUC、精度、召回率和F1值4种常用异常检测评价指标进行算法比较。不同方法的ROC曲线见图9。

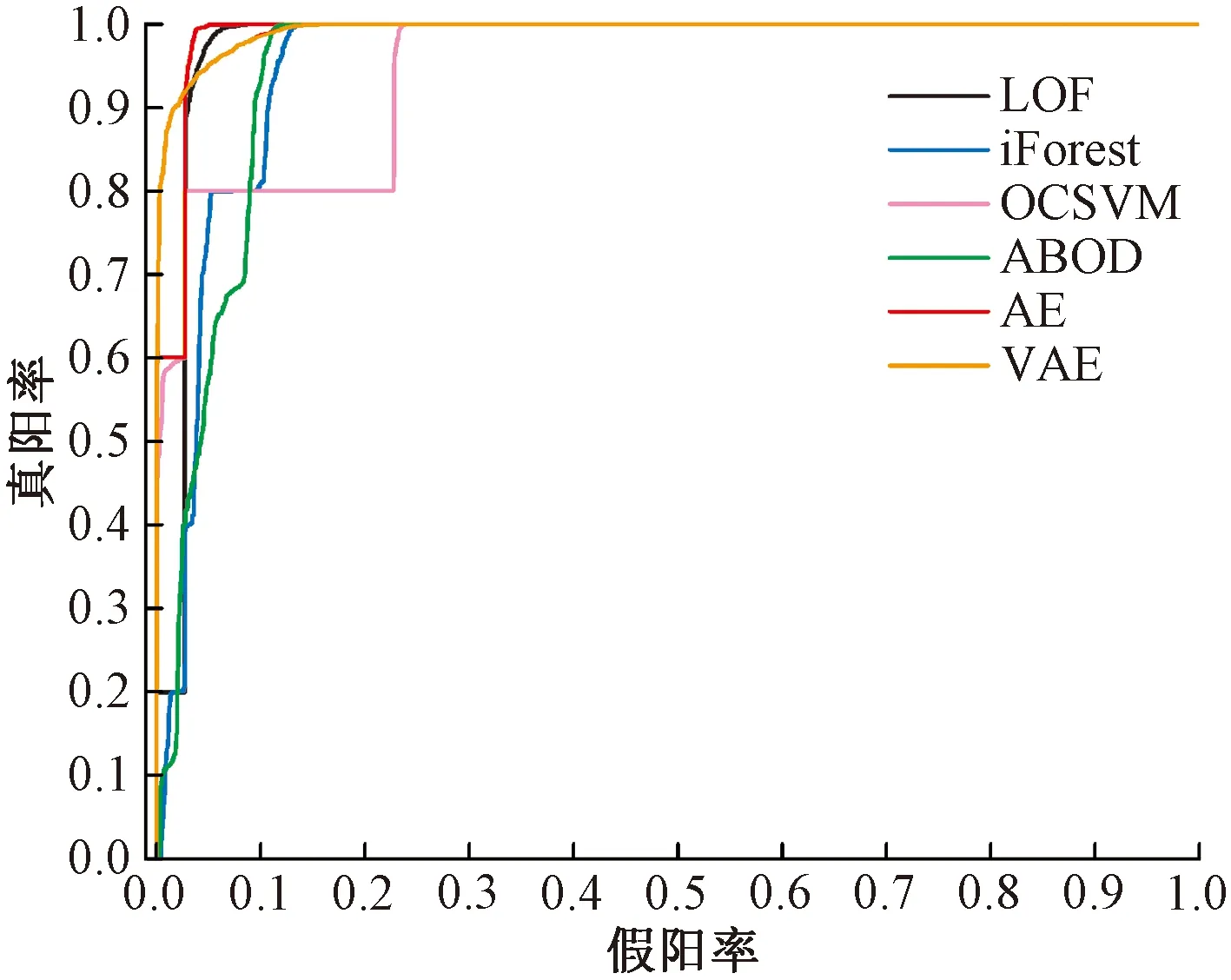
图9 ROC曲线比较

由图9可以看出，VAE的AUC值为0.992 6，略高于AE的0.988 7，高于其他传统方法，表明VAE能够更好地对MVB正常数据进行建模，并对多种不同异常数据具有更强的检测能力。实验结果对比见表2。VAE的F1值为0.945 3，高于AE的0.909 1，说明相比于AE的确定性映射关系，VAE是一种随机生成模型，具有更强的异常检测能力。VAE、AE的F1值均高于其他传统方法，这主要是因为深度神经网络在处理高维度数据和挖掘高可分性特征方面具有优势。同时，传统方法通常都有严格的数据假设，当训练数据与数据假设不一致时，其异常检测表现会受到较大影响。

在本文训练集下，VAE、AE的训练时间分别为429.15、347.18 s。由于VAE需要根据隐空间分布对隐变量进行多次采样，并计算输入测试数据与其平均重构数据之间的重构误差，因此其训练时间大于AE。在实际应用中可以通过提升计算性能来降低离线训练时间。在本文测试集下，VAE、AE的在线测试时间分别为0.217、0.186 s，两者相差不大，能够满足实际需要。

4 结论

(1)本文提出了一种基于VAE的MVB网络异常检测方法，无需人工特征提取，直接将MVB网络信号物理波形数据作为模型输入，选择模型重构误差作为异常检测指标。

(2)采用半监督学习方式，训练阶段只需要正常数据，解决了实际应用中异常数据不足的问题。

(3)利用KDE方法，不依赖于异常数据和专家经验，只需要正常数据就可以自动设置异常检测阈值。

(4)设计了MVB网络设备通信性能健康指标，为MVB网络设备通信状态监测提供了依据。

(5)在实验室环境下搭建MVB网络实验平台，模拟断路、端接、短路等5种典型故障，通过对比实验验证了本文提出方法的优越性和有效性。

未来将重点探讨本文方法对于电磁干扰故障、通信节点软硬件故障等更多故障类型的适用性。