三种非赫兹滚动接触模型的对比研究
王 平,周佳仪,王攀杰,陈 爽,安博洋
(1.西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都 610031;2.西南交通大学 土木工程学院,四川 成都 610031;3.成都工业职业技术学院 轨道交通学院,四川 成都 610031)
铁路运营速度的不断提高使得轮轨服役环境日益严苛,钢轨波浪形磨损、钢轨剥离、车轮多边形磨耗等轮轨伤损现象也更为严重[1]。因此,更为准确地模拟轮轨滚动接触力学行为,对于预测轮轨滚动接触疲劳和磨耗具有十分重要的意义。以往的模拟研究中[2-3],为了提高计算效率,常采用基于椭圆假设的赫兹接触理论。然而,实际情况下的轮轨接触斑常为非椭圆形状,使用赫兹理论会造成较大的计算误差。轮轨非赫兹滚动接触模型可以更准确地描述轮轨的接触斑形状及接触应力分布,从而能够更好地预测轮轨磨耗及滚动接触疲劳。
在模拟轮轨非赫兹滚动接触的研究中,业界学者开发了两类准确的计算模型。其一是通过有限元方法建立的数值模型,但是此种方法需要对轮轨结构进行精细的网格划分,因此在计算过程中需要进行庞大的矩阵计算,极大地限制了运算速度[4-5]。另外一种是基于半空间方法建立的边界元方法,其中最为典型的代表是Kalker开创的三维弹性体非赫兹滚动接触理论及其数值模型CONTACT[6-7]。该理论是目前业界最广为接受的理论,但是其计算效率因不断迭代而难以提高,因此尚未广泛应用于轮轨损伤的计算。
为了更高效地计算非赫兹滚动接触问题,学者们发展了一系列快速解法。Piotrowski等[8]提出了虚拟渗透的概念,通过引入衰减系数以忽略材料弹性变形的影响,提出了一种快速求解轮轨法向接触问题的近似方法(下文简称为KP模型)。LINDER等[9]也提出了类似的思路,但通过不同方法来计算轮轨接触斑和接触应力。Liu等[10]考虑摇头角的影响对KP模型进行了更深一步的扩展。文献[11]同样在KP模型的基础上发展了一种考虑弹性变形与法向压力分布关系的改进模型,使计算不再依赖于接触原点。另一种基于虚拟渗透方法的经典模型是文献[12]提出的半赫兹接触模型,该模型将渗透区域沿滚动方向划分为数个条带,并假定每个条带满足赫兹接触条件,从而求解出接触区域以及应力分布,并发展了STRIPES的数值程序。与STRIPES类似,文献[13]考虑材料弹性变形的影响,提出了一种新的方法——ANALYN来解决轮轨法向接触问题[13]。而以上简化模型切向问题的处理均采用改进的FASTSIM方法[8,12]或FaStrip模型[13]。其中改进FASTSIM方法的核心是将非椭圆接触斑等效为一个或多个局部椭圆,以求解出新的柔度系数替代原方法中根据椭圆假设计算的系数。
针对上述非赫兹接触模型,文献[14]比较了KP、LINDER和STRIPES三种方法求解S1002-UIC60接触工况时法向与切向结果的差异。文献[15]详细分析了KP、STRIPES、LINDER三种模型与FASTSIM程序在曲线地段进行切向计算的差异。文献[16]也对典型接触模型在法向以及切向方面的计算差异进行了对比,并分析了不同接触模型对轮轨伤损模拟的影响。文献[17]针对道岔转辙器区以CONTACT程序为参照,对比分析了不同赫兹接触模型,包括KP模型、STRIPES模型以及ANALYN模型在法向接触行为以及切向接触行为方面的计算差异。上述研究均表明,简化的非赫兹接触模型的精度对轮轨型面的依赖性很大,且只针对有限的接触工况进行对比,故其适用范围存在一定的局限性。因此,仍然需要一个系统、全面的对比研究,考虑不同型面类型,对大量工况进行计算,比较不同的简化非赫兹模型在不同接触工况下的计算差异。
本文选取我国高速铁路常见的两种标准车轮型面(LMA、S1002CN)与标准CHN60钢轨匹配时的两种典型工况进行详细接触计算,并以CONTACT程序的结果作为参照。借助UM软件输出大量工况,采用统计的思想,系统全面地调查不同模型在计算轮轨滚动接触行为时的精度与适用性,为轮轨损伤计算的模型选择提供可靠的依据。
1 三种非赫兹接触简化模型描述
1.1 KIK-PIOTROWSKI计算模型
KIK与PIOTROWSKI提出了一种快速、近似解决轮轨法向接触的新方法(以下简称“KP模型”)。在轮轨接触中,以接触点为坐标原点定义局部坐标系,x为纵向,正方向代表车轮滚动前进方向,y为横向,可以通过右手法则确定。该方法在法向接触建模中,假设两物体之间可以相互穿透,采用经验系数(ε=0.55)与渗透量的乘积来确定接触区域,并认为接触区域内的压应力分布应与纵向接触边界一致。其纵向接触边界a(y)及法向接触应力分布p(x,y)为
( 1 )
( 2 )
式中:f(y)为接触点附近沿横向的法向间隙;δ为渗透量;R为接触点处车轮半径;p0为接触原点的法向接触应力。
切向接触问题的求解则采用修正的FASTSIM模型进行处理。该方法的核心思想是将非椭圆区域等效为一个椭圆,根据该椭圆的具体参数确定FASTSIM中的柔度系数。详细介绍可参见文献[8]。
1.2 STRIPES计算模型
同样基于轮轨虚拟穿透的基本原理,AYASSE和CHOLLET在一系列推导过程的基础上发展了半赫兹的简化模型STRIPES。将接触斑沿滚动方向分解为若干条带,并假设每个条带的特征与赫兹接触理论相同。通过修正接触点区域的相对曲率,求解轮轨渗透量确定接触区域内法向接触应力的分布。每个条带中的纵向半轴长度a(y)以及接触斑内法向接触应力p(x,y)为
( 3 )
( 4 )

切向接触计算时仍采用修正的FASTSIM模型,不同于KP模型将整个接触斑等效为一个椭圆,STRIPES模型视每个条带均通过一个虚拟椭圆中心,在赫兹理论中使用条带中心处的相对曲率来确定局部虚拟椭圆长短半轴,由局部虚拟椭圆参数计算每个相应条带的柔度系数,随后根据原始FASTSIM方法进行切向接触应力计算。具体详见文献[12]。
由于运动副连续接触,使运动副的销轴与套圈中心始终保持运动副间隙的距离.可以将各运动副间隙假设为无质量的刚性杆.刚性杆长度为运动副间隙量,即r=(r1,r2,r3,r4),各刚性杆与X轴正方向的夹角称为运动副间隙角,记为α=(α1,α2,α3,α4).用刚性杆表示运动副间隙,运动副间隙角反映销轴与套圈的接触位置的变化.
1.3 ANALYN计算模型
SICHANI提出了一种不同于虚拟渗透法的近似分析方法,该方法不再忽略表面变形的影响,而是通过接触面之间的间隙估计接触表面变形,并通过修正渗透量求得接触区域。该方法认为接触区域的边界应满足:接触物体之间的法向间隙等于物体之间法向刚体穿透量与接触表面法向弹性变形量之差。接触斑的纵向和横向边界及法向接触应力为
( 5 )
( 6 )
( 7 )
式中:α(y)、β(y)、n(y)、r(y)为每个条带处由赫兹理论计算所得的参数;A(y)、B(y)为每根条带上的赫兹计算参数,即条带中心处的曲率;p0(y)为每个条带上的最大接触压力。
切向接触问题的解决以KALKER的条带理论和线性理论为基础,发展成一种名为FaStrip的新模型。该方法在计算过程中使用统一的柔度系数,根据每个条带处的相对曲率参数确定虚拟椭圆的长短半轴,并判断每个条带处于黏着区或滑动区,从而获得对接触滑动区域分布的准确估计。详细介绍参见文献[13]。
2 典型工况下轮轨非赫兹滚动接触分析
2.1 典型工况的选取
为了对比上述三种非赫兹快速模型的计算差异性,以KALKER的CONTACT程序的计算结果作为标准参考。所考虑的典型工况为LMA、S1002CN两种车轮型面分别与CHN60钢轨匹配时轮轨接触斑在钢轨顶面的分布情况。其中,轮对横移量变化范围为-3~6 mm,LMA和S1002CN车轮名义滚动圆半径分别为430、460 mm,轮对内侧距和轨距分别为1 353、1 435 mm,轨底坡设置为1/40,轮对轴重14 t。特别指出,由于本文所考虑的简化模型均假设轮轨接触斑沿纵向满足赫兹型接触假设,故本节的模拟工作忽略了轮对摇头角的影响,而轮对摇头角引起的横向蠕滑率则在下文中加以考虑。
不同轮轨型面匹配时的接触斑形状以及法向应力分布随横移量的变化见图1。为了便于比较分析,选取LMA型面非赫兹程度较小、接触斑形状接近椭圆,即横移量为0 mm时作为非极端工况代表。由图1(j)可知,S1002CN型面在6 mm横移量下接触斑非赫兹程度比较大,因此选取该工况作为极端工况代表。从接触斑形状、法向接触应力分布以及切向黏滑区域分布等方面对两种工况进行计算,分析不同非赫兹程度下三种模型的计算精度以及适用性。

图1 不同轮轨型面匹配下,轮轨接触斑形状以及法向应力分布随轮对横移量(-3~6 mm)的变化
2.2 轮轨法向非赫兹接触分析
图2为不同接触工况下三种简化接触模型与CONTACT程序计算的接触斑面积、最大法向接触应力以及接触区域内横向曲率分布,其中,图2(a)~2(c)为LAM型横移量为0 mm时的接触工况,图2(d)~2(f)型为S1002CN横移量为6 mm时的接触工况。如图2(a)~2(c)接触斑形状非赫兹程度较小时,三种简化接触模型得到的接触斑形状与CONTACT计算结果基本吻合。而随着非赫兹程度的增大,快速模型的计算误差也逐渐增大,但ANALYN的计算结果始终保持与CONTACT程序最为接近。由图2可以看出,KP模型总是高估了接触斑面积,致使相应法向接触应力偏小,说明以0.55倍的虚拟渗透量值作为实际渗透量并不完全准确。根据KP模型压力分布公式计算出的压力分布形状类似于接触斑的边界,在接触斑非赫兹程度较大时会产生较大的误差。在给定的载荷下,接触斑面积越大,接触斑内分布法向应力越小,因此KP计算所得分布法向应力总小于CONTACT。此外,值得注意的是,LMA型面的横向相对曲率分布比较平滑,而S1002CN廓形的横向相对曲率分布存在较大的跳跃波动,甚至会出现负值,违背了赫兹理论中曲率恒定的假设,进而对依赖于局部曲率进行计算的STRIPES模型、ANALYN模型产生一定影响,也是造成接触斑非赫兹程度较大的主要原因。

图2 不同接触模型计算不同工况时法向接触对比
2.3 轮轨切向非赫兹接触分析
轮轨接触斑上相互接触的质点对之间存在的相对滑动会引起接触区域内的切向力,又叫做蠕滑力,是引起轮轨磨耗接触疲劳和伤损的主要因素,也是车辆轨道动力学研究的重要输出量。因此,需要对不同型面接触产生的切向力以及黏着区域分布进行分析。分析过程中忽略摇头角以及侧滚角等的影响,因此横向蠕滑力为零,纵向蠕滑率ξxL,R、自旋蠕滑率ξnL,R为[18]
( 8 )
( 9 )
式中:rL,R为左右轮瞬时滚动圆半径;r0为名义滚动圆半径;δL,R为左右轮接触处的接触角。图3、图4是两种典型工况下蠕滑黏着区域的分布,接触斑内颜色的深浅代表蠕滑应力的大小,零点代表接触点的位置。每种接触模型计算所得切向力数值见表1。

图3 LMA型面横移量0 mm时轮轨黏滑分布

图4 S1002CN型面横移量6 mm时轮轨黏滑分布

表1 不同型面不同横移量下的纵向、横向以及总蠕滑力
3 基于统计思想的轮轨非赫兹接触简化模型适用性分析
为了检验以上简化模型对于车辆动力学工况的适用性,借助适用于多体系统运动学、动力学建模和仿真计算的UM软件构建CRH2单节车辆模型进行仿真分析,从而获得接触计算所需的基础参数。图5为单节车辆模型。

图5 单节车辆模型
根据多体动力学理论,将CRH2型车视为非线性多刚体系统,单节车辆由15个刚体组成。构架与轮对通过一系悬挂装置连接,车体与构架通过二系悬挂装置连接,采用不同的铰接约束车辆中各刚体的运动。采用LMA、S1002CN两种我国常用廓形车辆与CHN60钢轨匹配,设置速度为250 km/h,分别通过不平顺直线以及平顺曲线地段,并设置两种不同摩擦系数(f=0.3、f=0.5),从UM软件中输出蠕滑率等计算参数,将其作为输入参数导入CONTACT程序以及MATLAB编制的KP模型、STRIPES模型、ANALYN模型中进行计算,将不同模型的计算结果与CONTACT进行对比,采用统计中累计分布的思想对误差进行处理,对比简化接触模型的计算精度,计算流程见图6。需要强调地是,本节的研究目的是通过动力学计算获得大量的轮轨动态响应,以便于从统计的角度分析不同非赫兹接触模型的适用性,因而仅考虑了一种车型的参数。

图6 计算流程
3.1 直线地段
模拟车辆通过不平顺直线轨道,研究车辆不平顺对不同接触模型计算精度的影响。在直线轨道上施加德国高速不平顺谱,获得S1002CN、LMA车轮型面与CHN60钢轨匹配时的横向、纵向、自旋蠕滑率以及横移量等参数,其概率分布见图7。然后将已获得的接触参数分别代入三种简化接触模型以及CONTACT程序进行法向及切向接触计算。

图7 UM软件输出不同型面接触参数概率分布

图8 不同接触模型计算LMA型面接触时累积误差分布
使用UM软件输出不同接触型面匹配时的接触参数作为接触模型的输入量,采用三种非赫兹接触模型进行计算,并以CONTACT模型计算结果作为参考值,得到大量工况下几种接触参数的计算结果,采用统计的思想求得三种模型对CONTACT的误差累积概率分布。横坐标表示与CONTACT模型计算结果相比产生误差的数值,纵坐标表示达到该误差值工况的出现概率。UM软件输出不同型面接触参数概率分布见图7。由图7可知,车辆在不平顺直线地段行驶时所得蠕滑分布较为集中,且S1002CN型面产生的自旋值会略大于LMA型面。根据2节的结果可知,由于型面接触范围内曲率存在较大的波动,S1002CN型面在大蠕滑条件下会产生较大误差。采用不同接触模型计算LMA、S1002CN型面接触时蠕滑力累积分布分别见图8、图9。由图8、图9可知,S1002CN廓形下计算得到的各项接触参数累积误差要大于LMA廓形。在不同接触模型对同一接触参数的计算中,图9表明ANALYN模型总能获得最优结果;KP模型虽然预测详细接触解时存在一定的不准确性,但在计算接触参数时多数情况下可以得到不错的结果;而STRIPES模型相对最差。此外摩擦系数的变化不会影响接触参数以及法向接触计算,因此接触斑面积、最大法向接触应力以及总法向力不变。而由图8、图9可以看出,提高摩擦系数对切向计算的影响不大。

图9 不同接触模型计算S1002CN型面接触时蠕滑力累积误差分布
3.2 曲线地段
模拟车辆在50 m的直线轨道上行驶,然后通过400 m过渡曲线,进入半径为3 000 m的曲线。通过UM软件获得S1002CN、LMA车轮型面与CHN60钢轨匹配时的横向、纵向、自旋蠕滑率以及横移量等参数,其概率分布见图10。将已获得的接触参数分别代入三种简化接触模型以及CONTACT程序进行法向及切向接触计算。

图10 UM软件输出不同型面接触参数概率分布
由图10可见,车辆由直线逐渐过渡到曲线地段时蠕滑分布较为分散。不同接触模型计算LMA型面、S1002CN型面的接触参数累积误差分布分别见图11、图12。由图11、图12可知,S1002CN型面接触参数的计算误差要大于LMA型面,且通过对比图8、图9可以看出,曲线地段的接触计算误差略大于不平顺直线地段,原因在于曲线地段会产生较高比例的高蠕滑。与直线地段类似,随着摩擦系数的提高,各模型切向计算的精度差异不大。在曲线地段,KP模型的计算精度与ANALYN模型基本一致,甚至高于ANALYN。
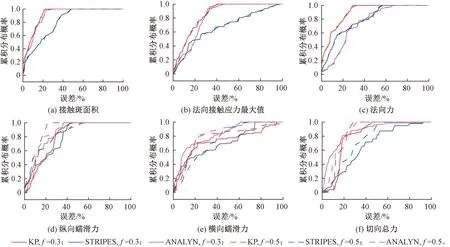
图11 不同接触模型计算LMA型面的接触参数累积误差分布

图12 不同接触模型计算S1002CN型面的接触参数累积误差分布
以上内容均从计算精度的角度对不同非赫兹滚动接触模型进行了对比分析,而车辆动力学求解和轮轨伤损计算要求接触模型的求解效率越快越好,不同接触模型在同一台笔记本电脑上计算同一工况所需时间见表2。其中,CONTACT程序所需时间最长,约为119.2 s;三种快速计算模型中KP模型的计算时间最短,约为CONTACT程序的1/397;ANALYN模型与STRIPES模型所需时间较KP模型较长。需要指出地是,本文所用的 KP模型、STRIPES模型以及ANALYN模型都是编写的MATLAB程序。而CONTACT是在Kalker原始算法基础上经过Vollebregt优化后的求解程序[19]。

表2 不同模型同一工况计算时间对比
4 结论
本文采用目前最常见的三种非赫兹接触模型从轮轨法向接触和切向接触两个方面对我国高速车轮廓形LMA以及S1002CN与CHN60钢轨匹配时进行计算分析,研究了不同非赫兹接触模型计算差异,根据计算结果得到以下结论:
(1)三种简化模型的计算精度在处理LMA-CHN60接触工况时最优,该接触工况下,接触斑形状接近于椭圆形,非赫兹程度较小,三种快速计算模型得到的接触斑形状、接触区域面积以及最大法向应力值与CONTACT计算结果基本相同。
(2)S1002CN廓形存在明显的局部曲率突变,更易产生非赫兹程度较大的接触斑,简化模型的计算精度在处理此类接触问题时较差。ANALYN模型在计算黏滑区域分布方面与CONTACT的结果最接近,因此计算详细局部黏滑分布时建议采用ANALYN模型。
(3)宏观法向以及切向力的计算中ANALYN模型与KP模型均能得到一个较好的结果,而STRIPES模型在某些工况下会产生较大的误差,不够稳定,需要改进其曲率平滑方法以改善计算结果。相比于ANALYN模型,KP模型的计算过程简单,计算时间短,因此只计算宏观接触力时建议采用KP模型。
为了能够兼顾动力学计算与轮轨伤损研究的需要,这三种非赫兹接触模型都需要进一步完善,以提高在不同接触条件下的计算精度。需要指出的是,本文的分析仅针对标准的轮轨型面,而对于磨耗型面的影响则并未涉及,这部分工作有待在下一步研究中进行开展。

