MIMO通信模型下的相关矩阵组低复杂度设计

施育鑫，鲁信金，孙艺夫，雷 菁，李玉生

(1.国防科技大学第六十三研究所，江苏 南京 210000；2.国防科技大学 电子科学学院，湖南 长沙 410000)

0 引言

矩阵常常被用于表示无线通信、图像视频处理、计算机视觉、相控阵雷达的数据表示。随着用户需求的不断增加，数据规模、通信阵列的持续扩大，矩阵的大小和维度也随之快速增加，这给矩阵的数据存储、算法计算带来了很大的困难。矩阵的关联性是指矩阵数据在某些维度上的相关特性，例如视频中时间相邻的帧具有很强的矩阵关联性。因此，充分挖掘矩阵间关联性，以实现低复杂度的计算具有十分重要的价值和意义。

1 问题描述

对于所给定复数矩阵H={Hj,k}，Hj,k∈M×N,j=1,2,…,J;k=1,2,…,K。其中，矩阵之间以及同一矩阵的元素之间有一定的相关性，包括：相同j下标、不同k下标的矩阵间存在一定的关联，即{Hj,1,Hj,2,Hj,3,…,Hj,K}间存在关联；且矩阵的各个元素间也存在关联，矩阵Hj,k∈M×N，j=1,2,…,J;k=1,2,…,K可表示为：

(1)

此外定义矩阵组H={Hj,k}的一组数学运算，其中间结果V={Vj,k}由式(2)给出：

(2)

式中，j=1,2,…,J;k=1,2,…,K，svd(·)为矩阵奇异值分解(Singular Value Decomposition，SVD)中求解右奇异向量的过程；Vj,k是由Hj,k的前L个右奇异向量构成的矩阵,维度为N×L。

为得到最终输出结果W={Wj,k}，先将不同j下标、相同k下标的Vj,k进行横向的拼接，得到维度N×LJ的Vk=[V1,k,…Vj,k,…VJ,k]，然后根据式(3)获取Wk：

(3)

式中，σ2为固定常数；Wk维度同Vk；I为单位矩阵，维度为LJ×LJ。

最后将各Wk按如式(4)进行拆解：

Wk=[W1,k,…Wj,k,…WJ,k]，

(4)

式中，Wj,k为Wk中顺序排列的子矩阵，维度为N×L。

为了降低计算和储存的复杂度，分析相关矩阵组的关联性，通过建模对输出结果进行估计，建模过程可用式(5)表示：

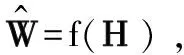
(5)

(6)

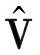
定义W的建模估计精度为：

(7)

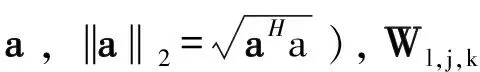
为描述方便，额外定义W的最低建模精度为ρmin(W)：

(8)

计算复杂度定义为由矩阵组H计算得到结果矩阵组W所需要的总计算复杂度。复数矩阵运算可拆解为基本的复数运算，而基本的复数运算又可进一步拆解为基本的实数运算。例如，复数乘法(a+bj)(c+dj)=(ac-bd)+(ad+bc)j的复杂度为4次实数乘法和2次实数加(减)法。实数基本运算的复杂度按照表1计算。

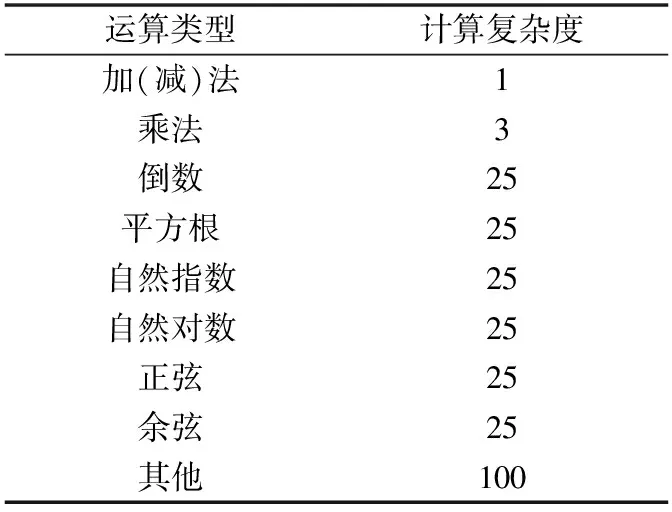
表1 实数基本运算的计算复杂度

2021研究生数学建模A题提供的数据集附件(Data1～Data6)给出的详细数据，包括输入矩阵组、标准中间矩阵组和标准输出矩阵组的数据及其维度，其中M=4,N=64,L=2,J=4,K=384,σ2=0.01，数据为十进制格式。根据所给数据Data1～Data6中的M=4，N=64,J=4,可对应通信模型中共有J=4个用户，每个用户的发射天线数为M=4，基站的接收天线数为N=64。L=2表示取信道衰落程度最低的2个信道向量，即对矩阵进行压缩。K表示信道探测时隙数。σ2表示信道中高斯白噪声的噪声方差。

2 通信模型建立

建立基于矩阵的多输入多输出(Multiple-Input Multiple-Output，MIMO)通信模型[1]如图1所示，J个用户发送信息，信号经过信道H到达基站，基站有N根接收天线。

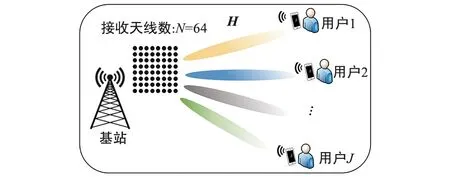
图1 矩阵关系的通信模型建立示意图Fig.1 Schematic diagram of establishing communication model of matrix relationship

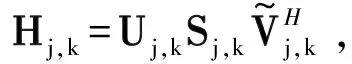
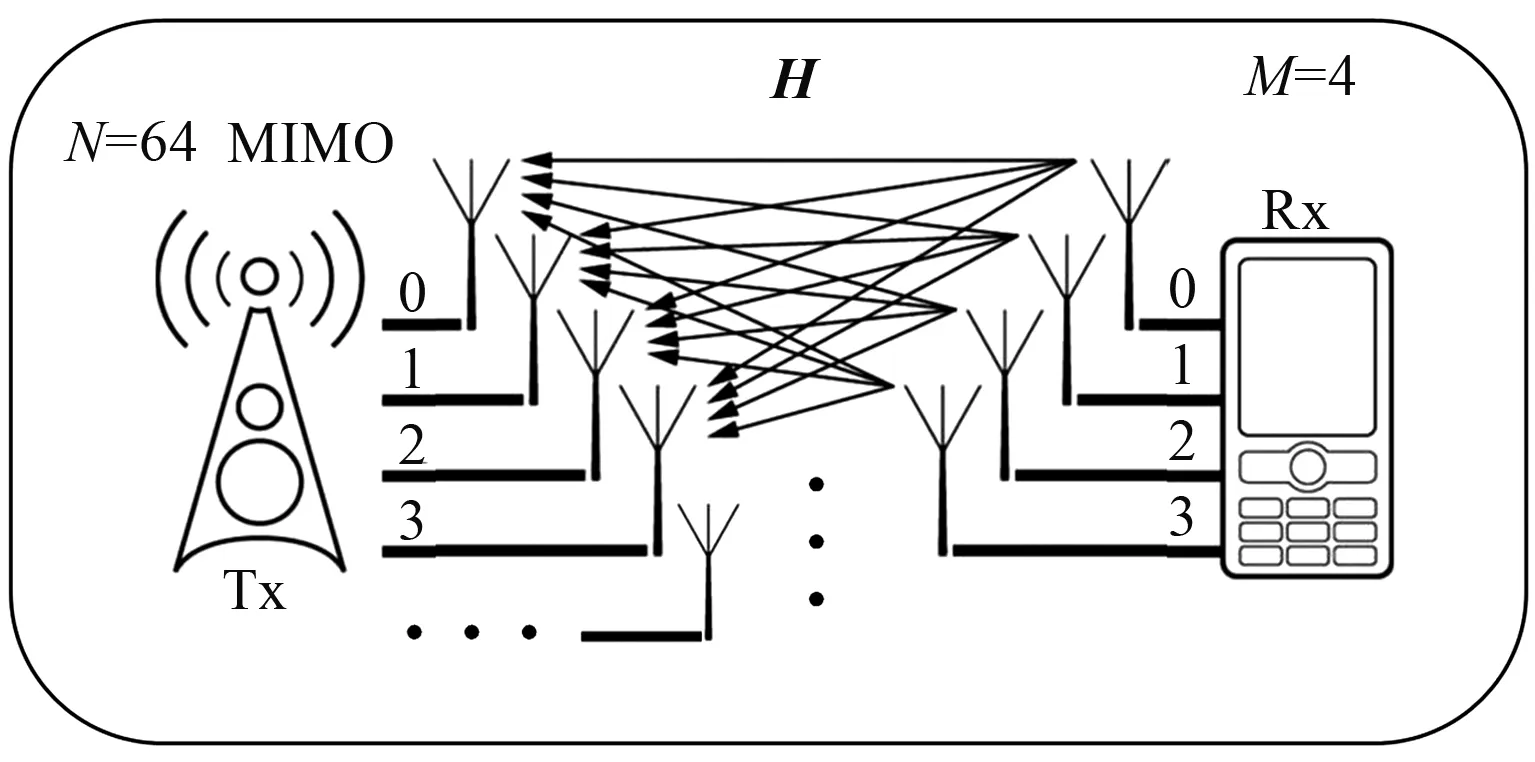
图2 单个用户和基站的通信示意图Fig.2 Schematic diagram of communication between a single user and a base station

此时，可使用压缩矩阵Vj,k来表示H矩阵。进一步，引入最小均方误差(Minimum Mean Square Error，MMSE)的概念来解释题设条件。如图3所示的信道模型中，信号x经过信道V=Vj,k，由于白噪声n的影响，接收信号y可表示为：

y=Vx+n。

(9)

图3 信号传输模型(求解MMSE流程)Fig.3 Signal transmission model (process of solving MMSE)

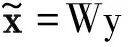
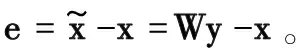
(10)

此时的MMSE为：

MMSE=E{eHe}。

(11)

假设接收到的数据y和误差e是不相关的，即

E{e·yH}=0。

(12)

将式(10)代入式(12)可得：

E{(Wy-x)·yH}=0。

(13)

将式(13)左边进一步展开可得：

E{(Wy-x)·yH}=E{WyyH}-E{xyH}=

WE{yyH}-E{xyH}。

(14)

由式(13)和式(14)可得：

W=E{xyH}E{yyH}-1。

(15)

接下来对E{yyH}和E{xyH}进行处理，首先对于E{yyH}，将其进一步展开：

E{yyH}=E{(Vx+n)(Vx+n)H}=

E{VxxHVH+VxnH+nxHVH+nnH}。

(16)

此处假设输入信号x和噪声n不相关，则nxH与nxH值为0，可得：

E{yyH}=E{VxxHVH+nnH}=

VE{xxH}VH+E{nnH}=

V(P·I)VH+σ2·I，

(17)

式中，P为发送信号x的能量，σ2为噪声n的方差。

其次对于E{xyH}，展开如下：

E{xyH}=E{x(Vx+n)H}=

E{xxHVH+xnH}=

E{xxHVH}=

E{xxH}VH=

(P·I)VH。

(18)

得到E{yyH}和E{xyH}后，将其代入式(15)可得到W的表达式：

W=E{xyH}E{yyH}-1=

(P·I)VH(V(P·I)VH+σ2·I)-1=

P·VH(PVVH+σ2·I)-1=

VH(VVH+·I)-1。

(19)

当发送信号x的能量P为1时，则可得：

W=VH(VVH+σ2·I)-1。

(20)

综合上述分析，MIMO模型中利用信道数据计算信道的MMSE均衡器接收矩阵的复杂度主要来源于SVD分解与式(20)中的矩阵求逆。

3 相关矩阵组的低复杂度计算

由前文可知，H、V和W之间的关系可以由图4表示。

图4 H、V和W的关系示意图Fig.4 Relationship of H，V and W

3.1 利用相关矩阵组的关联性降低计算复杂度

利用相关矩阵组的关联性以降低计算复杂度，其具体分析及操作如下。

3.1.1 矩阵数据的关联性

对于信道系数复数矩阵H={Hj,k}，其中Hj,k∈M×N,j=1,2,…,J；k=1,2,…,K。因此，该矩阵是一个M×N×J×K维的信道矩阵，其中M表示接收天线的数量，N表示发射天线的数量，J表示用户数量，K表示时隙个数。

由前文建立的通信模型，对H矩阵内在的关联性进行分析。首先，Hj,k内部的关系可表示为不同天线构建出的不同信道之间的相关性。在一般高斯白噪声信道条件下，天线阵列之间固定的距离和入射角关系将带来一定的规律，但数据集中未能发现Hj,k内部可靠的相关特性。这可能是由于天线之间的方向性、距离之间的差异较大，使得信道在空间上的相关特性不再明显。

考虑不同k时隙,同一用户j的信道系数情况，即MN个信道的时间相关性。图5给出了MN个信道在时隙k=1，2，3情况下的幅度响应和相位响应。可以看出，在不同k下的幅度和角度的变化程度不大，这可以理解为在相关时间内，信道的变化很小，这进一步验证通信建模的可行性。

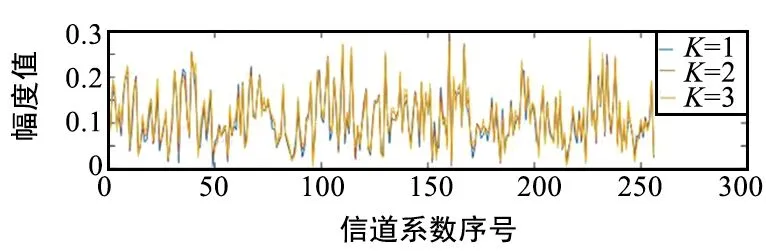
(a) 不同信道系数的幅度响应

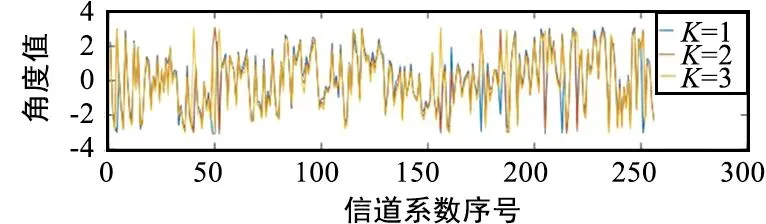
(b) 不同信道系数的相位响应图5 同j不同k的H块之间的幅度和相位响应关系Fig.5 Amplitude and phase response relationship between blocks H with the same j and different k

基于上述两层分析，得出Hj,k块在时间维上的相关性。而在时间维上利用SVD与MMSE求W矩阵是独立的，无法直接用于算法简化，为此，本文利用时间相关性，并运用插值算法直接估计W矩阵。

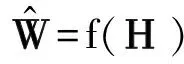
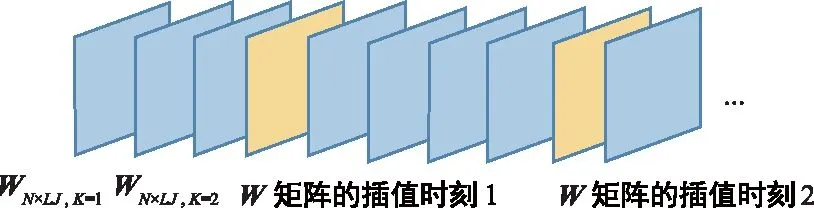
图6 W矩阵的插值示意图Fig.6 Schematic diagram of interpolation of W matrix

3.1.2 矩阵数据W的插值算法

对于矩阵数据W的插值算法，采用linear插值法、spline插值法与Pchip插值法进行建模插值[2-4]。此处，引入“最大插值比”作为评估方法来评价插值性能，参数寻优的过程可以表示为：

(21)

式中，R表示每隔R个点进行一次插值运算。因此，式(21)表示插值结果满足最小建模精度的约束下，使得插值数量越多的寻优目标。

因此，为满足题设对于拟合后W矩阵对最小建模精度的要求，需选择合适的插值方法并计算最大插值比，为此进一步提出了最大插值比搜索方法，以评估在不同信道条件数据集下可用的插值参数，最大插值比搜索算法的详细过程在算法1中给出，其基本思想为通过给定的初始插值比Rate，和选定的插值类型，不断迭代和逼近给定插值类型下的满足要求的最大插值比。当取得的插值比越大时，意味着W矩阵的更多部分可以通过在K维度上的相关性插值得到，不需要通过SVD与MMSE求逆过程，这将大大减少计算的复杂度。此外，Data集最大插值比的计算过程可以理解为适应信道的训练过程。在后续过程中，在外部信道条件未剧烈改变的情况下，不需要再次执行，因此最大插值比搜索可以在线下执行，不会影响算法的复杂度。

算法1 所提出的最大插值比搜索算法输入:训练数据集Data,包含通过MMSE计算的标准W矩阵;初始化:初始插值比 Rate=1/R,插值间隔R的初始值可以设定为R=2。R的中止值可以设定为Rmax=200选定的插值类型:Linear,Spline,Pchip。执行过程:ForR0.99,则跳出循环 (break) Endif EndifEndif输出:插值类型,最大插值比Rate

表2给出了3种常见插值方法在6个Data集的最大插值比。

由于Data1～Data6来自不同的信道条件，因此同一插值方法在插值过程中计算出的最大插值比有较大区别。例如Data 3数据集的最大插值比显著较小，这可以理解为信道的时变性强或受到干扰噪声较大，插值算法在此时难以满足要求，需要降低最大插值比。

进一步，横向对比3种插值方法，可见在多数的数据集下，Linear插值的最大插值比最小，性能最差，这是由于简单的Linear插值精度较低。Spline插值与Pchip插值的最大插值比性能相近，Spline插值在Data 1与Data 3上表现比Pchip插值较好。从原理上分析，可以理解为当基础函数振荡时，Spline比Pchip更好地捕获点之间的移动，后者会在局部极值附近急剧扁平化，这在该场景下带来了更好的插值性能[5-6]。

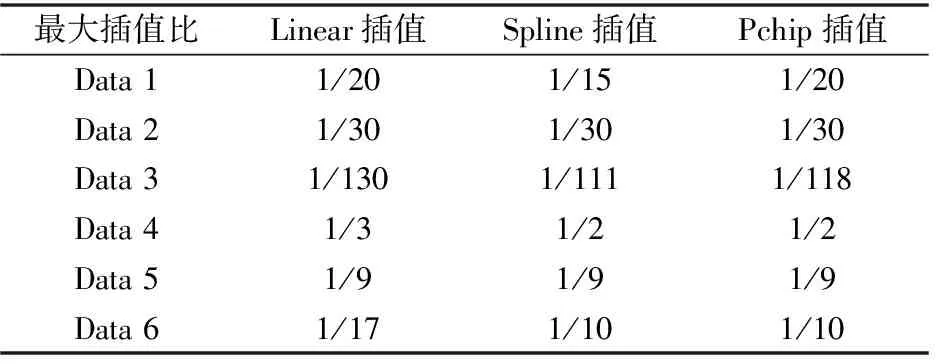
表2 3种插值方法在6个Data集的最大插值比

复数矩阵运算可拆解为基本的复数运算，而基本的复数运算又可进一步拆解为基本的实数运算，实数基本运算的复杂度按照表1计算。

对于Linear插值法，根据上述描述，可得需要加减法6次、乘法2次、倒数1次，且对于复数，幅度和相位要分别插值，总复杂度是实数插值的两倍。然而，特殊的是这里插值点的横坐标是均匀的，因此计算的复杂度可以大大简化，仅需要3次加法、2次乘法和1次倒数，因此总复杂度为68。每个插值时刻k，共需要NJL次插值，因此需要复杂度68NJL。本文的参数取值为N=64,J=4，L=2，因此计算复杂度为17 408。

对于Spline插值法，其计算步骤为：求三次函数的系数，然后将插值点横坐标代入三次函数，计算又需要6次加法、6次乘法。且对于复数，幅度和相位要分别插值，总复杂度是实数插值的2倍，因此总复杂度为124，每个插值时刻k，计算复杂度124NJL。取本文参数，计算复杂度为31 744。

对于Pchip插值，由于其性能不如Spline且计算复杂度相似，因此不在此处进行考虑。

3.2 降低矩阵求逆的计算复杂度

首先，对于矩阵分块直接求逆，假设一个N阶(这里的N被重新定义)的方阵A，分块如下：

(22)

设A的逆矩阵分块如下：

(23)

则根据矩阵分块求逆的原理有：

(24)

式中，对于N×N阶矩阵，需要的矩阵相乘的运算量级为N3。

对于n>1，m>1，直接分块求逆算法在具体实现中需要利用递归实现，具体的运算量按照复数乘加次数统计，对于上述的直接求逆算法，以乘加次数统计理论运算量，式(24)各部分运算量：c11的运算量为4m2n+4mn2-mn，c12和c21的运算量相等，均为4m2n+4mn2-6mn，同理，c22的运算量为4m2n+4mn2-m2，为此，矩阵A利用一次分块求逆的总的运算量为：

T(1)(N)=T(m)+T(n)+16m2n+

12mn2-13mn-m2+4m3，

(25)

式中，T(1)(N)表示利用一次矩阵分块求逆算法计算矩阵求逆的总计算量，T(m)和T(n)分别表示对m和n阶复矩阵求逆所需的运算量。

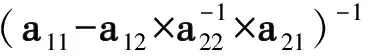
采用改进的Strassen矩阵求逆算法,结合式(22)～(23)，Strassen算法应用到求逆运算有如下公式：

(26)

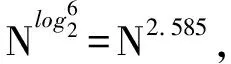
按照前面相同的运算量统计方法，根据式(25)，矩阵利用一次分块求逆的总运算量为：

T(1)=T(m)+T(N)+13m2n+

11mn2-4mn+3m2。

(27)

对于n>1,m>1，Strassen矩阵求逆算法也是利用递归实现的，但因为Strassen算法减少了矩阵复乘次数，所以相比直接分块的常规算法运算量有明显降低。

(28)

式中，对于N×N阶矩阵，需要的矩阵相乘的运算量级为N2。

为了便于比较新求逆算法的性能改善，按照前面相同的运算量统计方法，根据式(28)，矩阵A利用一次分块求逆的总的运算量为：

T(1)(N)=T(m)+T(N)+8m2n+8mn2+mn,

(29)

式中,T(1)(N)表示利用改进算法计算一次矩阵求逆的运算量，T(m)和T(n)部分表示对m和n阶复矩阵求逆所需的运算量。

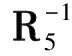
和矩阵直接分块求逆算法相比，新的求逆算法虽然增加了一些加减运算，但复乘次数降低。对于维数较高的矩阵，其中有大量的复矩阵运算，复乘消耗的运算量将远大于加减法，而这个运算量随着矩阵维数增加将有显著增大，因此新算法对于复乘次数的降低将显著改善求逆运算的实时性能。和常规Strassen矩阵求逆算法相比，改进的算法由于利用了求逆矩阵的特点，即对Hermite矩阵进行求逆运算，所以在运算量和算法复杂度上都有明显的降低。

常规算法计算一次矩阵求逆的计算复杂度如表3所示，改进算法计算一次矩阵求逆的计算复杂度如表4所示。

表3 常规算法计算一次矩阵求逆的计算复杂度

表4 改进算法计算一次矩阵求逆的计算复杂度

在本文中，当矩阵维度为8(J=4)时，改进算法总共复杂度为4 776，常规算法总共5 255，复杂度降低10.03%。

进一步，图7给出了不同用户数量J时，改进的Strassen算法与常规Strassen算法的复杂度比较。可以看出，随着用户数量增加，矩阵求逆时的维度增加，采用改进的Strassen算法对复杂度的降低更加明显。

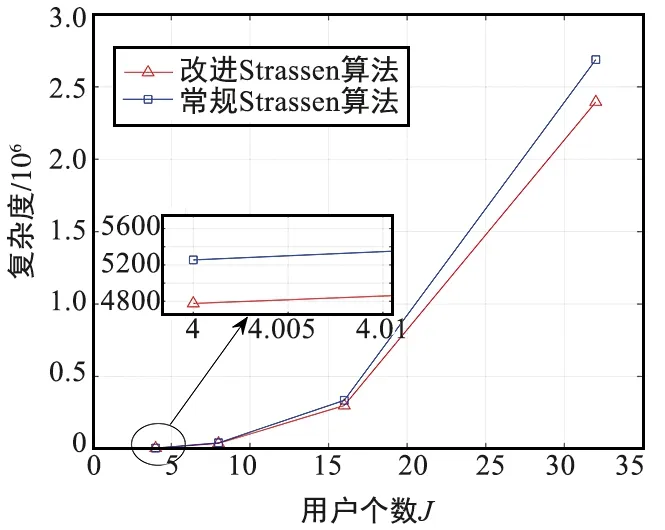
图7 在不同用户个数J下，改进的Strassen算法与 常规Strassen算法的复杂度比较Fig.7 Under different number of users J,the complexity comparison of the improved Strassen algorithm and the conventional Strassen algorithm

3.3 所提算法对最小建模精度的影响

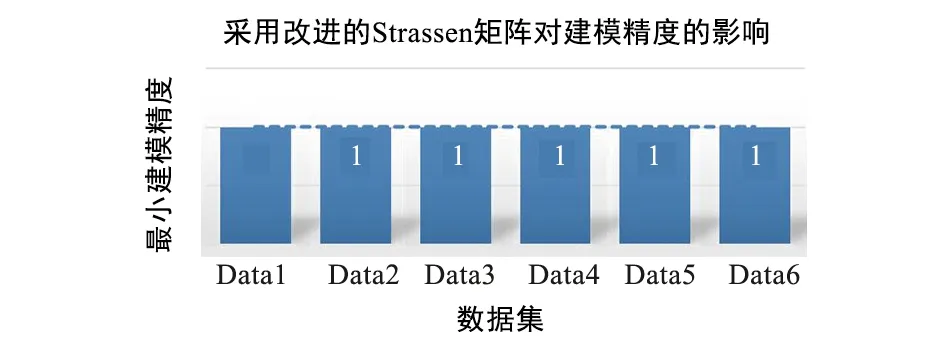
图8 采用改进的矩阵求逆算法后对各数据集 最小建模精度的影响Fig.8 Influence of the improved matrix inversion algorithm on the minimum modeling accuracy of each data set

3.4 综合复杂度分析

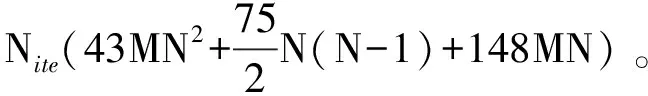
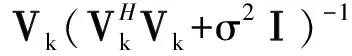
对于不采用插值算法的情况，每个插值时刻k，由H矩阵到W矩阵，需要进行J(J=4)次SVD和1次MMSE均衡(主要复杂度在于求逆)的计算。其中4次SVD需要3 574 400次计算。MMSE均衡需要521 112次计算，因此共需要计算复杂度C1=4 095 512。采用Spline插值时，每个插值时刻的复杂度为31 744。可以计算出每次插值的复杂度收益为C2=3574400+521112-31744 = 4 063 768。因此采用插值的最终复杂度收益为：

ΔC=(C1-C2)×K×Rate。

(30)

假设Rate=1/3时，ΔC=524 225 536。可见，插值对于计算复杂度的降低比较明显。同样，计算复杂度可以降低为：

(31)

当Rate=1/3时，计算复杂度降低为原来的66.93%。当Rate=1/10时，计算复杂度降低为原来的90.08%。

综上，当采用改进的Strassen矩阵求逆算法时，复杂度降低了10.03%。进一步采用插值算法后，计算复杂度能够在上述的基础上再降低9.92%(插值比为1/10)、33.07%(插值比为1/3)。

4 结论

本论文主要解决MIMO场景下的相关矩阵组的低复杂度计算问题，首先利用H矩阵在时间相关性推导了W矩阵的相关性，通过对已有W矩阵的相关性直接插值出部分缺失的W。这使得在接收H矩阵时，在求取部分W矩阵后通过相关性重建完整的W矩阵；也避免了一部分H矩阵的存储以及这部分H矩阵计算SVD与求逆获得W矩阵的过程。相比SVD与求逆的复杂度，插值的复杂度要低得多。此外，采用了一种改进的Strassen矩阵求逆算法来降低求逆过程的复杂度。该算法结合了Strassen矩阵求逆的高效性以及Hermite正定阵的共轭对称性特点，结构更简化。