基于外界影响及时序因素的PM2.5预测研究

杨艳梅,程宗毛

(杭州电子科技大学 理学院,浙江 杭州310037)

雾霾问题不仅对人体健康造成极大危害，也破坏了植被的正常生理机能，对天气及气候的影响十分显著。PM2.5作为雾霾的主要成分之一，是指大气中直径小于或等于2.5微米的颗粒物，其已成为影响城市空气质量的主要污染物之一[1-2]。

国内外已开展了关于PM2.5预测的研究，提出了一系列数据分析模型。PM2.5浓度预测方式大致分为两类：(1)时间序列分析预测法。将历史数据作为输入变量，利用传统统计模型或机器学习进行时间序列预测。例如，文献[3]利用传统的自回归滑动模型(Autoregressive Moving Average Model，ARMA)预测长沙市PM2.5浓度；文献[4]则利用北京市PM2.5浓度的历史数据训练机器学习中的长短期记忆模型(Long Short Term Memory，LSTM)来达到预测目的；(2)外界因素分析预测法。将PM2.5浓度成因作为输入变量，从影响因素着手提高预测模型的解释能力。例如，文献[5]利用平均温度、地表温度和平均风速等气象因素来进行基于BP(Back Propagation，BP)神经网络的PM2.5预测；文献[6]利用20种气象因素和6种环境因素建立了基于量子粒子群算法和径向基神经网络算法相结合的预测模型。上述两种方式各有优势，也都有一定的局限性。时间序列分析预测法突出了时间因素在预测中的作用，建立了时间序列内部关系，但其暂不考虑外界具体因素的影响，精确度有待提高。外界因素分析预测法忽略了PM2.5浓度自身的内部联系，且PM2.5的影响因素具有多样性，使得该方法无法保证对外界因素数据的收集及准确性。

本文兼纳了两种思路，采用BP-EEMD-LSTM组合模型进行预测。本文先依据主要外界影响因素建立基于BP神经网络的PM2.5浓度初步预测模型，此模型预测产生的残差序列中包含了时序因素。针对具有典型的非线性、非平稳性的复杂性较高的时间序列，如果直接建立预测模型，则很难达到预测精度要求[4]。为了降低时间序列复杂程度，本文先将残差序列进行集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)；然后完成复杂程度较低的分解分量的 LSTM建模，将各个分量的预测值累加得到最终的残差修正值；最后，将BP模型得到的初步预测结果与EEMD-LSTM得到的残差修正结果线性相加为最终的预测结果。本文通过实例证实了该组合模型在PM2.5日浓度预测方面有一定的优越性。

基于BP-EEMD-LSTM组合模型的PM2.5浓度预测流程如图1所示。

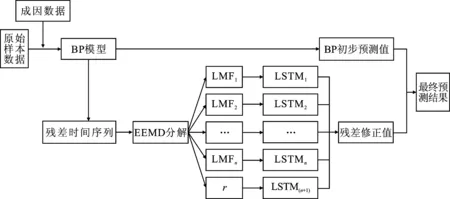
图1 预测流程图Figure 1. Flow chart of prediction

1 理论模型

1.1 BP神经网络

(1)

为了使得误差函数达到最小，利用梯度下降法反复修正权值ω和阈值b。假设η、α分别为权值和阈值的学习速率，则更新计算式为式(2)。

(2)

(3)

预测时，将规范形式的数据输入模型中，即可利用重复更新完成后的权值和阈值获得最终的预测值。

1.2 集合经验模态分解

研究人员于2009年提出了适用于分析非平稳、非线性复杂信号的EEMD(Ensemble Empirical Mode Decomposition)[8]，其可将复杂信号分解成若干个按频率高低排列的本征模函数(Intrinsic Mode Function，IMF)和一个趋势项。该分解算法在原信号中多次添加白噪声，利用白噪声序列均匀分布的频率改变信号极值点的特性，改善了经验模态分解(Empirical Mode Decom-position，EMD)的模态混叠现象[9]。EEMD的算法步骤如下[10-11]：

步骤1在原始信号x(t)中添加平均值为零，方差恒定的等长随机高斯白噪声ni(t)，得到一个新的信号xi(t)

xi(t)=x(t)+ni(t)

(4)

式中，ni(t)为第i次添加的白噪声；xi(t)为第i的新信号；

步骤2将噪声叠加信号xi(t)进行EMD分解，得到n个IMF分量ci,j(t)和一个趋势项ri(t)。

(5)

重复执行步骤1和步骤2共N次，计算每个分量以及余量经过N次实验后的平均值，可消除多次加入白噪声对真实IMF分量的影响，最终得到n个IMF分量c1(t)～cn(t)和趋势项r(t)。分解结果为

(6)

(7)

1.3 长短期记忆神经网络

LSTM作为一种时间递归神经网络，适用于处理和预测时间尺度较长的事件，并可避免梯度消失问题[12]。LSTM单元包括内部单元、输入门、输出门和遗忘门。长短时记忆网络主要通过“门”来丢弃或者增加信息[13]。LSTM单元结构图如图2所示。

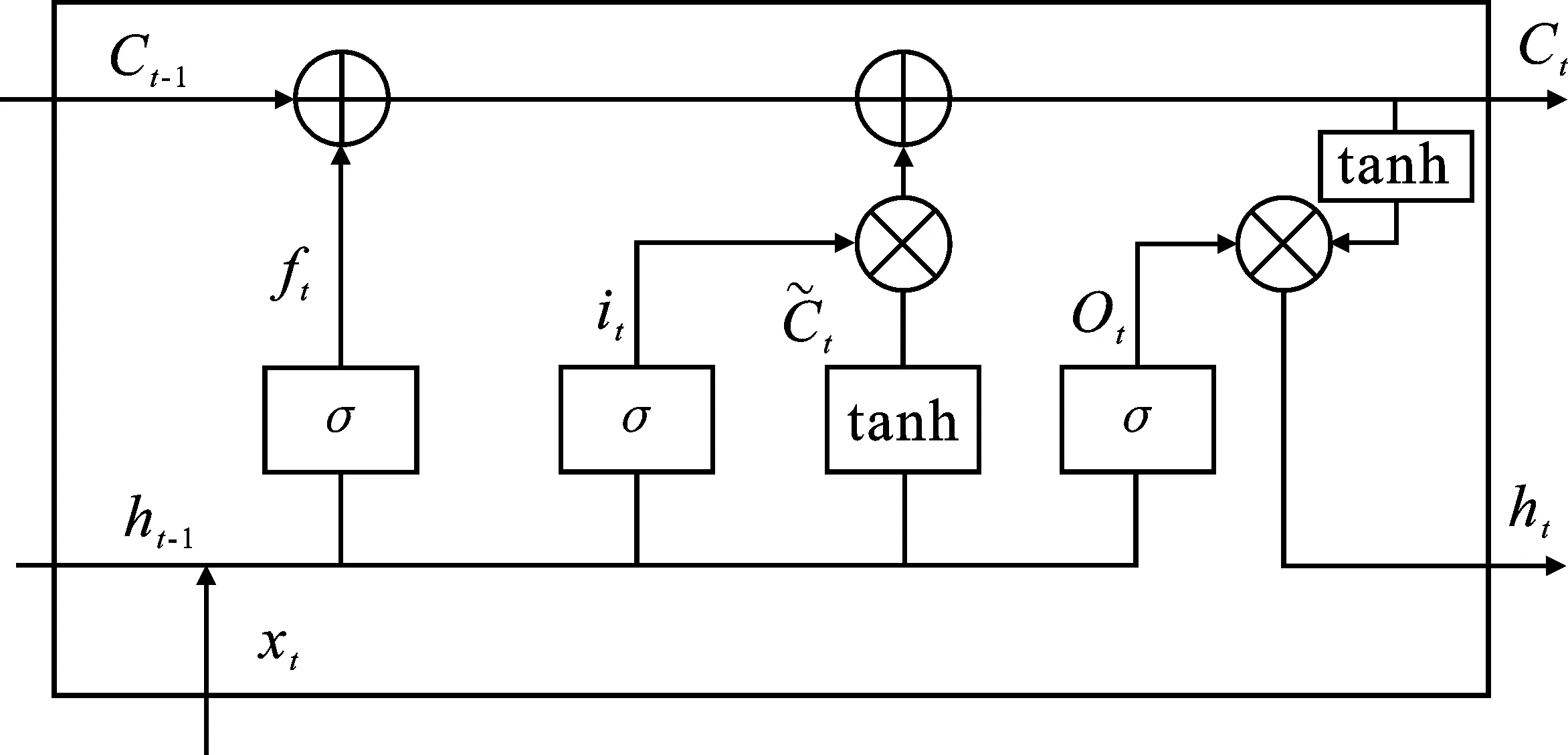
图2 LSTM单元结构图Figure 2. Architecture of LSTM cell

LSTM网络更新[14-15]为：

(1)遗忘门过程函数

ft=σ(Wf·[ht-1,xt]+bf)

(8)

式中，ft为输出遗忘率；σ表示sigmoid函数；Wf为遗忘门权重矩阵；ht-1表示上一时刻的输出结果；xt为该时刻的输入信息；bf为遗忘门的偏置项；

(2)输入门第1部分过程函数为

it=σ(Wi·[ht-1,xt]+bi)

(9)

式中，it为输出结果；Wi为输入门权重矩阵；bi为输入门的偏置项。输入门的第2部分由tanh函数产生1个候选向量为

(10)

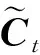
(3)每个单元更新后的状态表示为

(11)

式中，Cd为更新后的当前时刻的单元状态；Ct-1为上一次的单元状态；

(4)输出门的计算输出门结果Ot为

Ot=σ(Wo·[ht-1,xt]+b0)

(12)

式中，Ot为输出门；Wo为输出门权重矩阵；bo为输出门偏置项。利用Ot得出当时刻的记忆输出ht，如式(13)所示。

ht=Ot·tanh(Ct)

(13)

2 模型建立

本文基于BP-EEMD-LSTM组合模型进行PM2.5日浓度预测，组合模型分为以下步骤：

步骤1BP初步预测。将训练集主因素作为BP的输入变量，并将训练集PM2.5日浓度作为输出变量来训练此模型。将主因素输入训练后的BP模型，得到预测集的PM2.5日浓度BP初步预测值Yb和训练集的PM2.5日浓度BP预测值Ybt，并计算训练集的残差时间序列Ye=Yb-Ybt；

步骤2采用EEMD分解残差时间序列。步骤1产生的残差时间序列Ye通过EEMD分解，得到n个不同频率的IMF分量和一个趋势项；

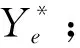
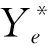
3 数据选取与预处理

本文相关数据来源于中国空气质量在线监测分析平台。选择来源于该平台的杭州市PM2.5、PM10、SO2、CO、NO2、O3的日浓度以及平均温度、最高温度、最低温度、平均相对湿度、总降雨量/总融雪量、平均风速和最大持续风速[16]共13个指标数据作为研究对象。将2014年1月1日～2019年5月31日的PM2.5日浓度和以上12个相关数据作为实验数据，设置2019年5月数据作为预测集，其它月份数据作为训练集，各因素与PM2.5日浓度的相关性如表1所示，相关系数越大表示关系越密切。

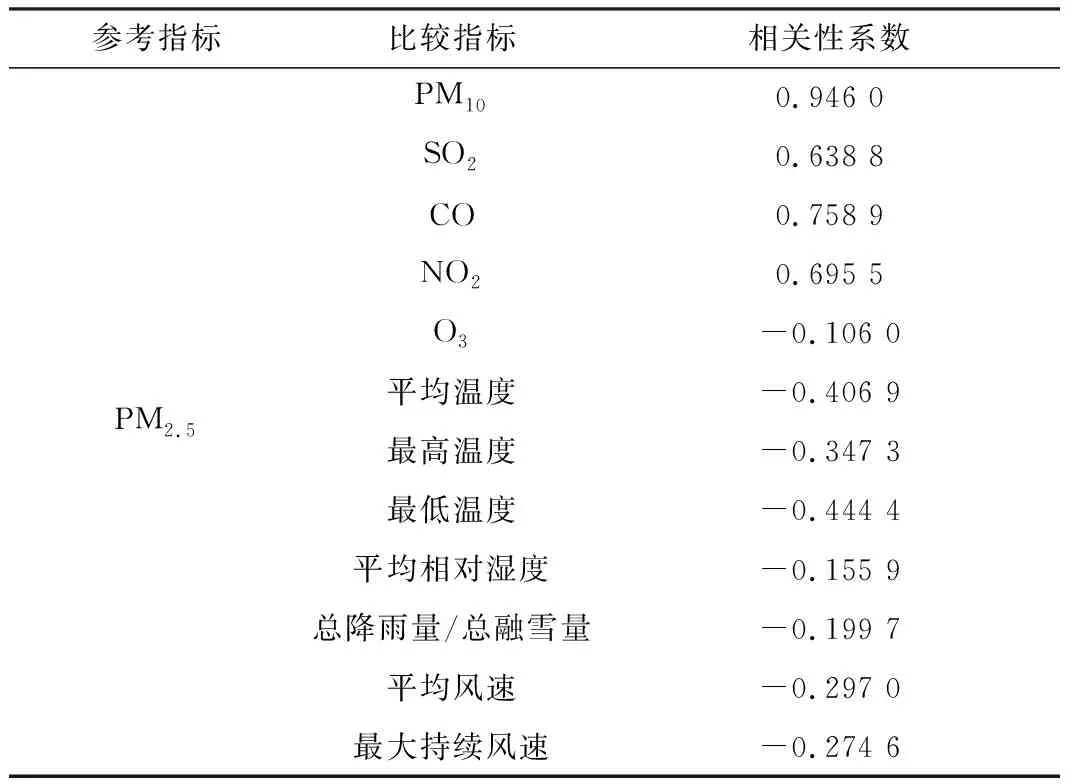
表1 相关性分析

由表1可以看出，在参与分析的因子中，PM10、SO2、CO、NO2是影响 PM2.5变化最主要的因素[16]，相关系数均达到了0.5以上。因此，本文选取PM10、SO2、CO、NO2日浓度作为影响PM2.5日浓度的主因素，PM10、SO2、CO、NO2日浓度也将作为BP预测模型的输入量。

4 实证分析

4.1 BP初步预测

由相关性分析可知，BP神经网络的输入数据包含4个特征，即PM10、SO2、CO、NO2日浓度，因此设立四输入单输出的BP模型，具体操作为：(1)模型隐藏层设置。构建3层隐藏层，将第1层神经元个数设为12，将第2层神经元个数设置为2，第3层神经元个数设为1，输入数据维度为4，采用tanh作为其激活函数；(2)模型参数设置。本文设置损失函数为绝对值均差(Mean Absolute Error，MAE)，选择随机梯度下降(Stochastic Gradient Descent，SGD)为优化器，为防止模型训练出现过拟合现象，设置Dropout(0.4)；(3)模型训练。设置学习步长为0.01；(4)模型预测。将外界成因数据输入训练后的模型得到预测集的PM2.5日浓度预测值Yb以及训练集的PM2.5日浓度残差值Ye。图3为此次BP模型初步预测值的结果，图4表述产生的训练集残差时间序列图。

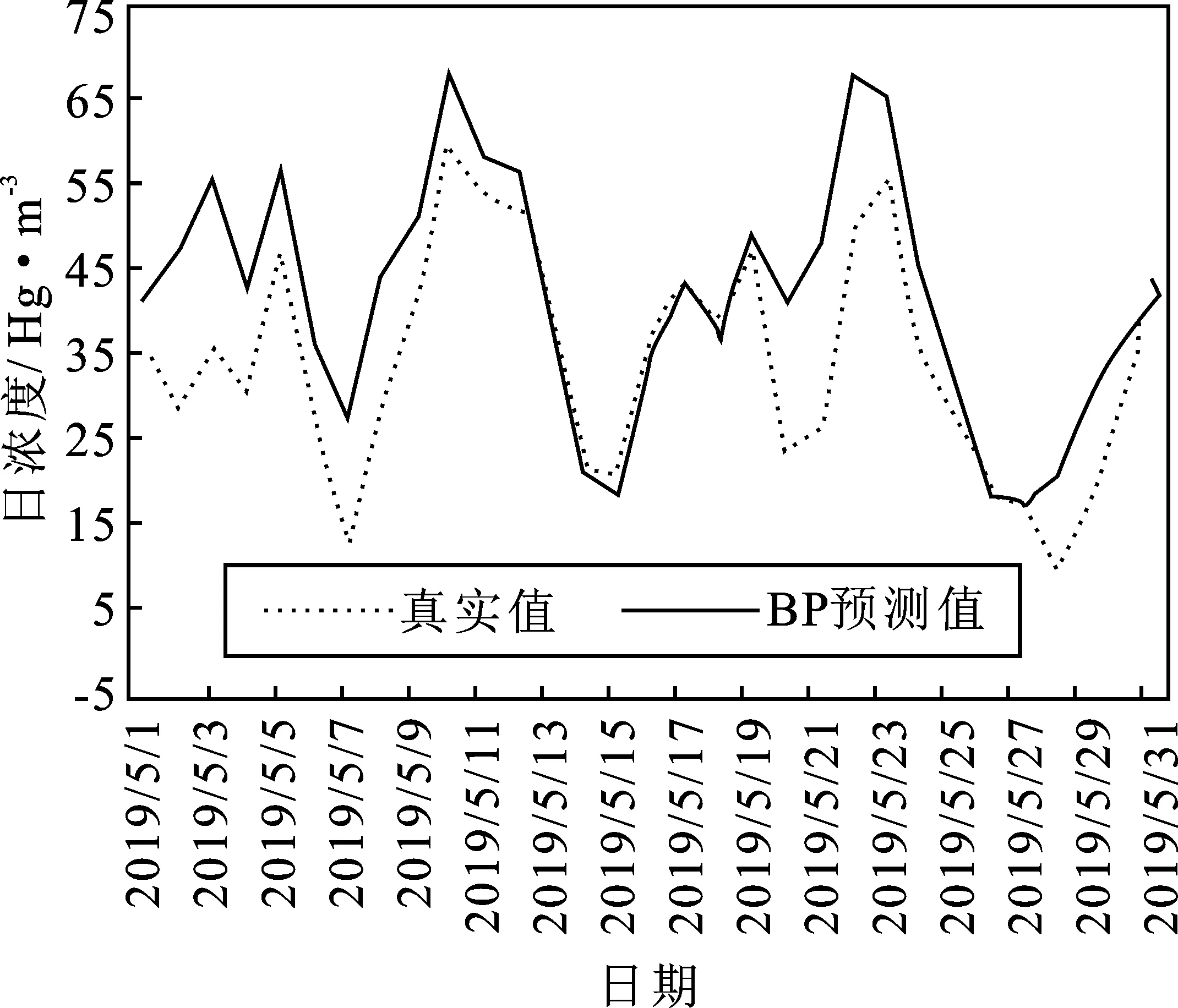
图3 BP预测值与真实值对比Figure 3. Comparison between BP predicted value and real value

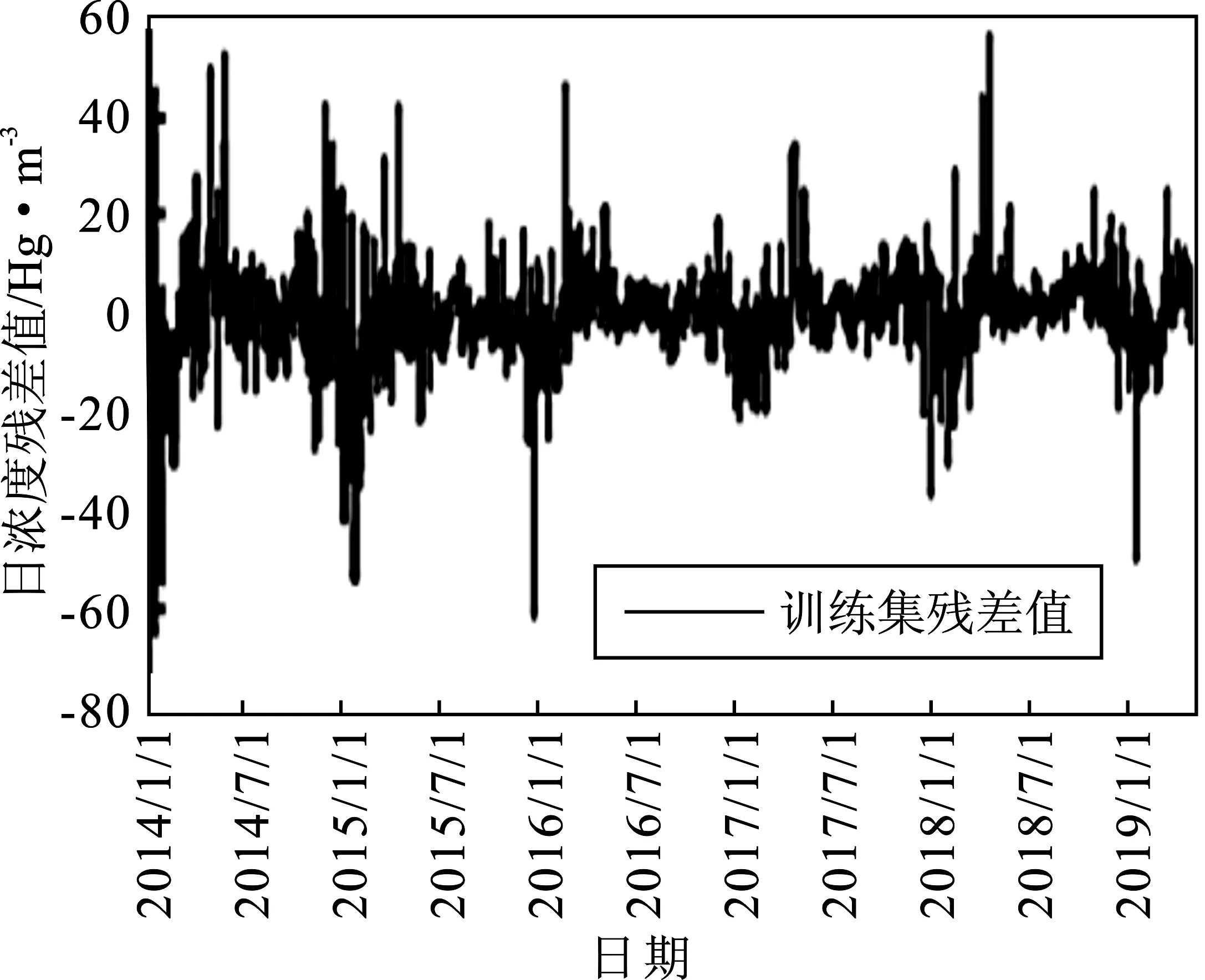
图4 训练集残差序列Figure 4. The residual series of training set

4.2 EEMD分解残差时间序列

将得到的训练集的残差时间序列Ye进行EEMD分解，得到10个不同频率且相对稳定的IMF分量c1～c10和趋势项r，如图5所示。原始残差序列通过EEMD分解后得到了变化规律更加明显的数据，进而降低了时间序列的复杂程度，减少了预测残差的难度。

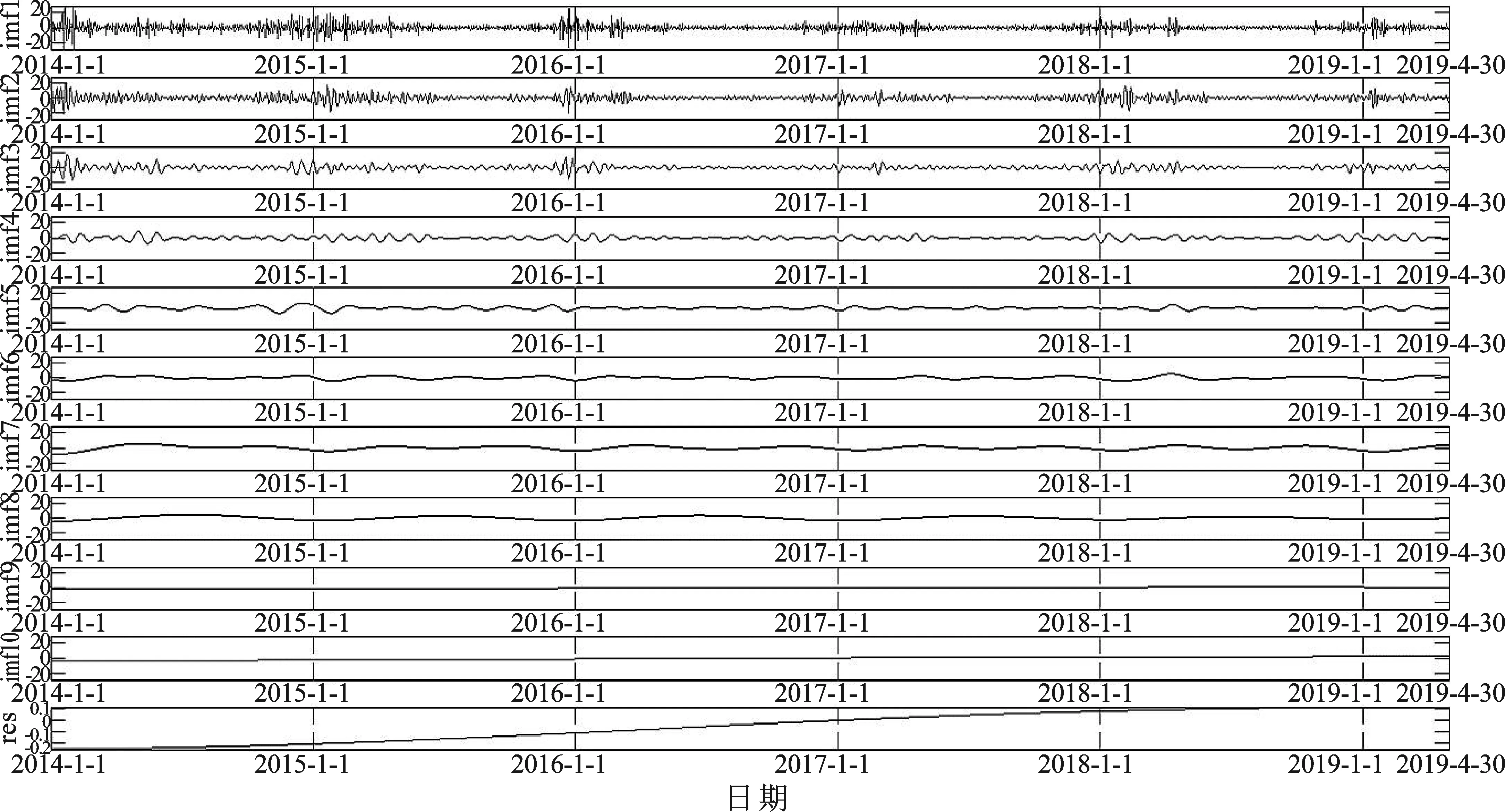
图5 残差序列的EEMD分解结果Figure 5. The decomposition results of residual series by EEMD

4.3 LSTM模型预测残差修正值

为了适用于训练LSTM，需要使用滑动窗口将各分量时间序列数据转换为监督学习型数据。假设LSTM模型每组输入数据长度为n，即为预测目标之前的n天分量数据，用“过去”预测“未来”。设置预测步长为1步，每次只能预测1个数据，之后将预测后的数据作为新的输入数据，从而实现模型的动态更新。输入数据及输出数据如表2所示。

表2 LSTM模型的输入输出数据

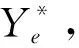
图6 基于EEMD-LSTM模型的残差修正Figure 6. The residual correction based on EEMD-LSTM model

4.4 结果分析

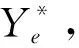
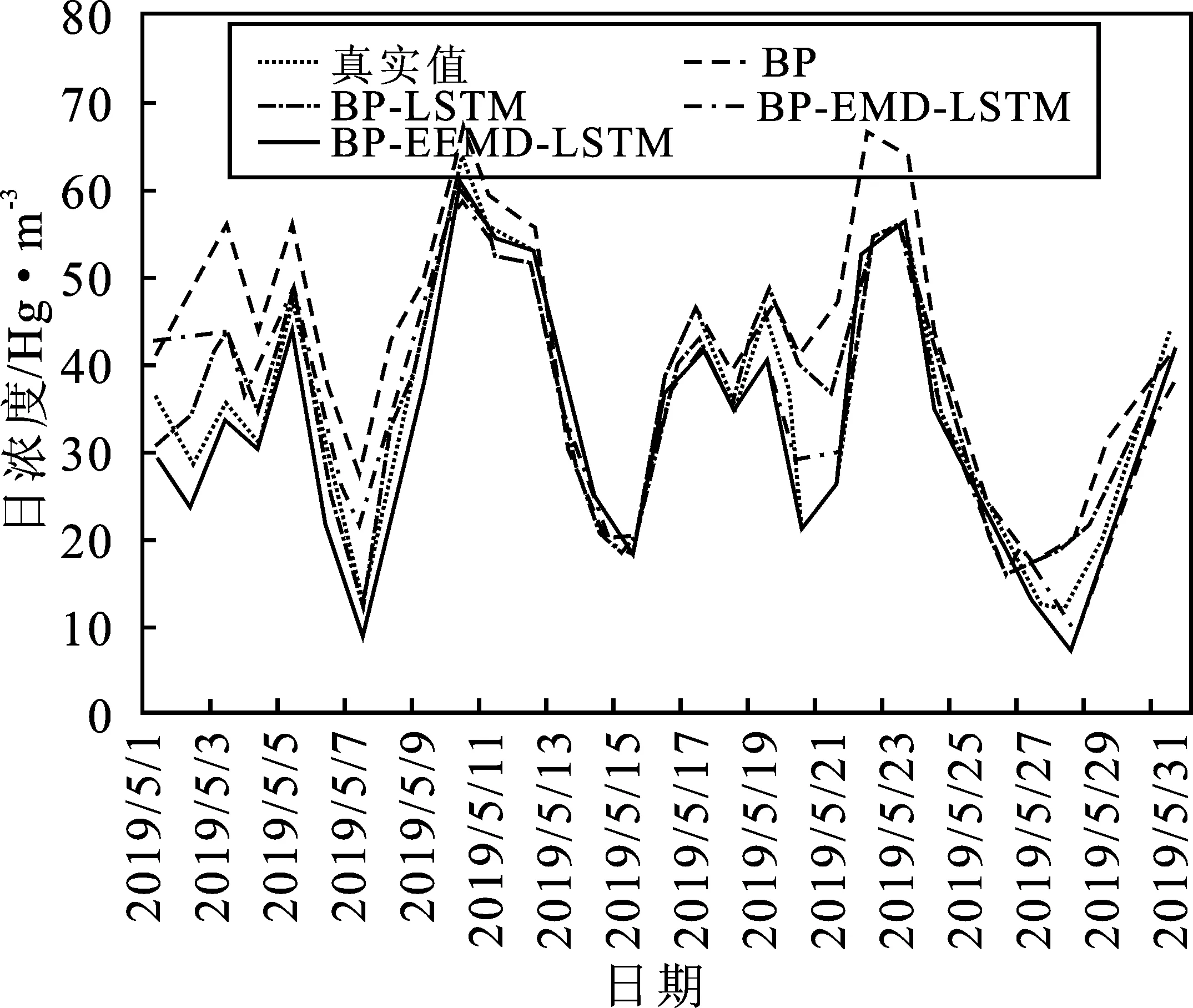
图7 各模型的预测结果对比Figure 7. Comparison of prediction results of each model

由图7可知，BP-EEMD-LSTM 组合模型具有良好的预测效果，能准确地预测出PM2.5日浓度整体变化趋势，并响应PM2.5日浓度的波动变化。BP 模型、BP-LSTM模型和BP-EMD-LSTM模型都能较好地预测PM2.5日浓度趋势，但BP 模型整体的预测准确度较差；BP-LSTM模型在5月1日～5月8日、5月19日～5月22日以及5月26日～5月30日预测存在较大误差；BP-EMD-LSTM模型则无法准确预测了5月1日～5月5日以及5月16日～5月19日的PM2.5日浓度。同时，本文采用均方根误差(Root Mean Squared Error，RMSE)、相关系数R和平均百分比误差(Mean Absolute Percentage Error，MAPE)来评测4种预测模型的性能，以便更直观地定量分析预测结果。比较分析结果如表3所示。

表3 模型预测的误差评估指标

由表3可知，本文提出的BP-EEMD-LSTM组合模型的相关系数更接近1，说明该组合模型能够较好地捕捉PM2.5日浓度变化趋势。该组合模型的均方根误差为2.74，较BP模型提高了73.4%，较BP-LSTM组合模型提高了54.4%，较BP-EMD-LSTM组合模型提高了26.5%。此外，BP-EEMD-LSTM组合模型的平均百分比误差为8.01，较BP模型提高了73.5%，较BP-LSTM组合模型提高了54.0%，较BP-EMD-LSTM组合模型提高了24.2%。由此可知，本文采取的预测模型比其他4种模型预测结果更加精确、有效，整体上BP-EEMD-LSTM组合预测模型的结果更接近真实值。

5 结束语

雾霾问题现在已成为中国大部分城市的主要空气污染问题之一，针对雾霾主要标志物PM2.5的浓度预测尤为重要[18-19]。影响PM2.5预测的因素较多，本文先利用相关性分析方法选择了相关性最大的4个指标作为预测PM2.5的主要外界因素；然后，将主要外界因素输入BP模型得到初步预测值与历史残差序列，再由EEMD-LSTM模型基于历史残差序列做时间序列预测，预测结果为残差修正值；最后，将BP初步预测值与残差修正值结合从而完成对PM2.5的预测。实验结果证明本文提出的基于外界影响及时序因素的PM2.5预测研究即BP-EEMD-LSTM组合模型具有更好的预测效果与精度，为PM2.5的预测研究提供了新的思路。

本文主要探讨了气象因素和大气污染物因素对PM2.5浓度预测的影响，其他因素(例如地理位置、环保政策等因素)仍有待进一步的探索研究。