基于MATLAB App Designer的牵引电机滚动轴承可靠性评估系统设计

齐美义,廖爱华

(上海工程技术大学 城市轨道交通学院,上海 2016202)

目前，可靠性系统设计已被应用到各个行业。文献[1]以双主轴双刀架数控机床的数控系统为研究对象，对该型数控系统进行了可靠性分析，并使用 VC6.0与OpenGL研发出可靠性系统。为进一步提升输电线路自然灾害风险的在线管控能力，文献[2]使用HTML语言进行开发，并利用JavaScript 和 TypeScript开发前端页面研发一套基于气象参数的输电线路电气可靠性评估系统。文献[3]使用 WebStorm 和 MySQL 数据库设计了电力骨干通信网可靠性评估系统，完成了电力骨干通信网可靠性的实际评估分析。文献[4]通过面向对象的编程方法，采用SQL和浏览器/服务器模式模式(Browser/Server，B/S)相结合的方式完成了铁路牵引供电可靠性评估系统设计。

MATLAB App Designer研发工具被国内外研究人员广泛使用。使用该工具研发的微波光子滤波器可以选择单模或多模光源[5]，还可以编辑频率响应参数，例如色散参数和光纤长度。文献[6]在MATLAB App Designer环境下完成了平面桁架结构计算系统设计。该研究首先创建桁架系统模型和输入数据的图形用户界面(Graphical User Interface，GUI)元素，在选项卡“静态分析”允许运行有限单元法(Finite Element Method，FEM)分析；然后显示位移、应力等结果。其“模态分析”选项卡用于计算特征值和振型，“优化”选项卡允许优化桁架系统的横截面和形状，用于减轻重量。文献[7]在比对各种算法后引入免疫算法(Artificial Immune Algorithm，AIA)，为配送中心的地址选取优化问题给出了基本解决思路，得出了求解步骤和求解方法。在解决选取最佳地址的过程中，主要考虑各个配送需求点的位置、配送需求量等，由配送中心辐射到其他需求点。MATLAB APP Designer则被用于研发物流配送中心选址优化系统。

本文基于MATLAB App Designer开发了牵引电机滚动轴承可靠性评估系统。针对牵引电机滚动轴承在运行过程中由于载荷不均匀和运行环境恶劣的问题，建立了基于MFO-WPHM(Weibull Proportional Hazard Model)的可靠性评估方法，并完成数据录入、数据分析和可靠性评估等模块设计。该系统以轨道交通基地实测的滚动轴承振动数据进行研究，实现了对牵引电机滚动轴承的可靠性评估，为城市轨道交通车辆的安全运行提供了重要保障。

1 威布尔比例故障率模型参数估计

比例故障率模型包含指数分布、威布尔分布、对数正态分布等，其中威布尔分布应用最为广泛。威布尔分布可以通过调整形状参数、尺度参数及位置参数来拟合现实的多种失效样本数据。其中形状参数的多样变化可以描述威布尔分布的3种失效率函数：递减的失效率函数、常数的失效率函数和递增的失效率函数。这3种失效率函数对应于浴盆曲线的3个阶段：早期失效、偶发失效和耗损性失效。该失效特征符合设备故障分布类型多样的特点[8]，因此选用Weibull分布作为基底失效率函数的WPHM为

(1)

式中，β是形状参数；η是尺度参数；α是协变量回归参数；Z为时间t时刻所对应的PCA[9-10]融合后的特征指标值。这里采用极大似然估计对β、η、α参数进行估计[11-12]。

求解威布尔比例故障率模型中的3个参数，需要采集原始振动数据。数据包含一定的故障数据和截尾数据。设收集的时间数据为(t1,t2,t3,…,tn)，待求解的参数集θ=(β,η,α)，得到似然函数为

(2)

式中，R(tj,θ)是可靠度函数；h(ti,θ)是故障率函数；N为样本集；D为失效集。

对似然函数两边取对数，得到

(3)

式中，n是数据总数；r代表n中有r个故障数据；n-r为截尾数据；Z(ti)为ti时刻的振动特征指标数值；Z(tj)为tj时刻的振动特征指标数值。

由极大似然参数估计原理，将lnL(θ)分别对待估参数β、η、α求偏导后得到一组非线性方程组。

(4)

由于常规算法求解该非线性方程组的计算速度较慢，本文将建立的极大似然方程组式(4)中每个方程的绝对值的和最小化为目标[13]；然后通过MFO算法进行参数估计优化，寻优得到WPHM的β、η、α，代入到式(5)所示的可靠度表达式中计算可靠度，绘制可靠度曲线。

(5)

2 基于MFO-WPHM的可靠性评估方法

2.1 飞蛾扑火算法

飞蛾扑火优化算法(Moth-Flame Optimization，MFO)[14-15]是于2015年提出的一种新的启发式智能算法。该算法的灵感来自飞蛾的横向导航飞行机制。飞蛾在夜间飞行时，对月亮保持一个固定的角度，这种行为使它们在长距离飞行时始终保持直线飞行。在现实中，飞蛾与火焰相距很近，当飞蛾看到火焰发出的光时，便会试图与其保持固定的角度飞行。飞蛾把人造光误以为月光，于是就有飞蛾绕着人造光作螺旋曲线运动，路径示意图如图1所示。

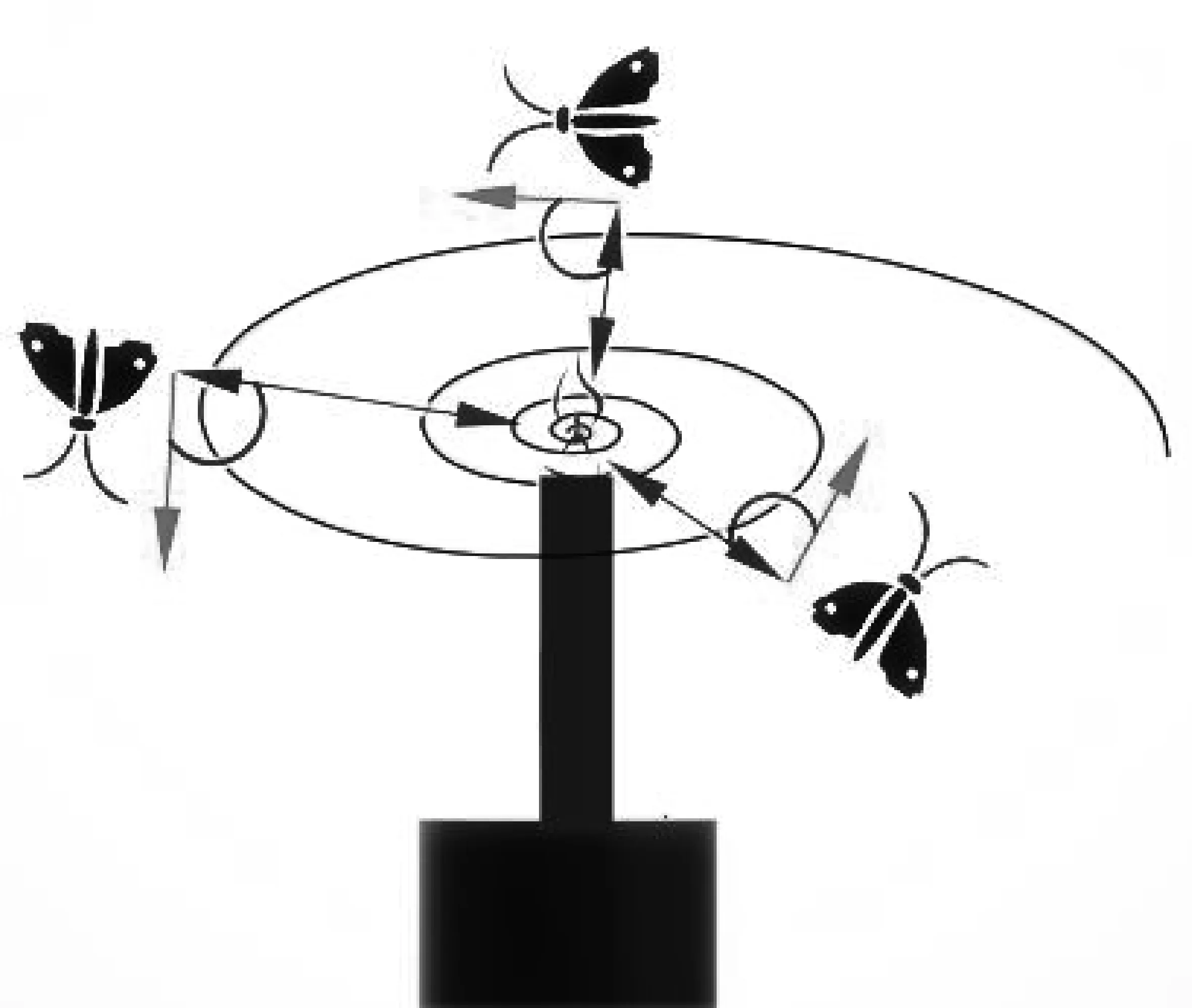
图1 靠近光源的螺旋状飞行路径Figure 1. Spiral flying path around close light sources

在MFO算法中，假设飞蛾为优化问题的候选解， 问题的变量是飞蛾在空间中的位置。通过改变位置矢量，飞蛾可以在任意空间中飞行。n个飞蛾在d维空间的位置为

M=(mi1,mi2,…,mid),i=1,2,…，n

(6)

数组OM用于存储飞蛾的适应度值

OM=[OM1,OM2,…，OMn]T

(7)

该算法的另一个核心部分是火焰，其火焰矩阵可表示为

F=(Fi1,Fi2,…,Fid),i=1,2,…，n

(8)

数组OF用于存储火焰的适应度值。

OF=[OF1,OF2,…,OFn]T

(9)

在MFO算法中，飞蛾和火焰都是解。它们的区别在于每一次迭代更新方式不同。飞蛾实际上是在搜索空间中移动的搜索主体，飞蛾获得的最佳位置用火焰表示。火焰可以看作是飞蛾在搜索空间时落下的旗子，每个飞蛾在旗子周围搜索，并在找到更好的解决方案时更新其位置。通过这种方法，飞蛾就不会失去它最好的解决方案。MFO算法是一个近似于优化问题的全局最优的三元组MFO=(I,P,M)。其中，I生成初始化解和计算相应的适应度值的函数，为I:ψ→{M,OM}初始化后，函数P:M→M成为主函数，循环运行，直到函数T:M→{true,false}。当满足终止条件时，返回true；如果不满足，返回false。在MFO中，对每只飞蛾的位置Mi和Mj进行火焰更新，选择对数螺旋S(Mi,Mj)作为飞蛾的主要更新机制，计算式如下

S(Mi,Mj)=Di·ebt·cos(2πl)+Fj

(10)

式中，Mi表示第i个飞蛾；Fj表示第j个火焰；b是一个定义对数螺旋线形状的常数；t是[-1,1]之间的随机数(其中t=-1是最接近火焰的位置，t=1是距离火焰最远的位置)；Di表示第i个飞蛾到第j个火焰的距离，可以由式(11)计算求得。

Di=|Fj-Mi|

(11)

飞蛾相对于n个不同位置的更新可能会降低对最优解的寻找。本文提出了火焰数量的自适应减少机制来提高开发能力，其定义如下

(12)

式中，l为当前迭代次数；N为火焰的最大值；T为最大迭代次数。

2.2 基于MFO-WPHM的算法寻优流程

利用MFO算法优化威布尔比例故障率模型的形状参数β、尺度参数η、协变量回归参数α，提高算法的寻优能力。算法寻优步骤如下：

步骤1初始化MFO算法参数。飞蛾种群数n，最大迭代次数T，搜素空间维度d，最大火焰数N，螺旋形状参数b；

步骤2初始化飞蛾位置和火焰矩阵。将处理过的数据集作为搜索空间，并在搜索空间中随机初始化n个飞蛾位置，计算每个飞蛾个体的适应度值，并将结果置于火焰矩阵中；

步骤3更新飞蛾位置与火焰数量。计算飞蛾与火焰间的距离并用利用式(10)更新飞蛾位置，利用式(12)更新火焰数量；

步骤4更新火焰矩阵。计算每个飞蛾个体适应度值，并将其同当代的火焰种群合并，将合并后的种群按照适应度从高到低排序，取前N个火焰位置，然后将其置于火焰矩阵中；

步骤5判断是否达到最大迭代次数。若当前迭代次数超过最大迭代次数，输出最优飞蛾种群个体适应度值所处空间位置Best_flame_pos，对应的坐标就是优化的参数β、η、α；否则更新种群并继续寻优。

2.3 基于MFO-WPHM的运行状态可靠性评估流程

采用主成分分析法(Principal Companent Anolysis,PCA)对提取的全部指标进行特征融合，并将融合后的特征指标作为WPHM的响应协变量，建立状态特征指标与可靠度之间的数学模型。用MFO优化算法估计WPHM的待定参数，得到具体的数学表达式。通过该模型计算出滚动轴承的运行状态可靠度，从而实现对牵引电机滚动轴承的运行可靠性进行评估。具体流程如图2所示。

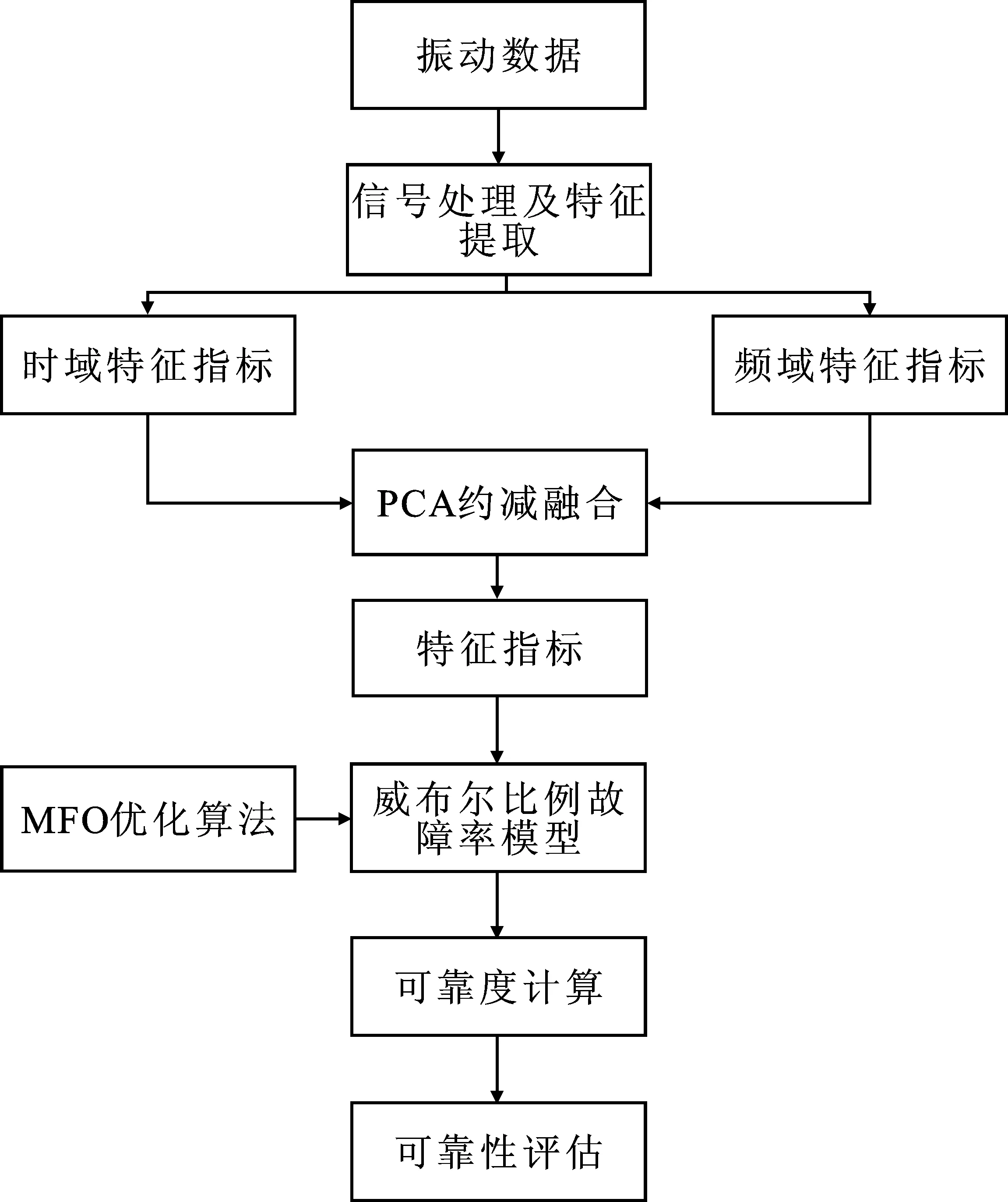
图2 运行状态可靠性评估流程图Figure 2. Flow chart of the operating reliability evaluation

3 牵引电机滚动轴承可靠性评估系统设计

3.1 系统概述

MATLAB专门以矩阵方式处理数据，具有强大的科学计算、图像处理、可视化、开放式和可扩展的功能。它与数值分析、矩阵计算、科学数据可视化以及系统设计、仿真和人机交互等功能集成在一个窗口环境中。其中MATLAB App Designer设计工具集成了构建布置可视化组件，可用于系统的布局和设计[16-17]，用户只需要将可视化组件拖放到设计画布中，系统即可自动生成面向对象的代码。

本文以MATLAB作为编译软件，建立牵引电机滚动轴承可靠性评估系统。首先打开MATLAB，在面板命令行输入“appdesigner”回车进入App Designer程序编辑界面。然后根据系统模块来分析所需要的组件搭建界面，新建的GUI包含两个文件：(1)包含Callback回调函数的M文件或一小段MATLAB程序。其中M文件包含子模块弹出的子界面窗口的控件；(2)包含GUI控件的fig文件[18-19]。该牵引电机滚动轴承可靠性评估系统的主界面及各级子界面由按钮(Push Buttons)、文本编辑框(Editable Texts)、日期选择(Data Picker)、表(UI Table)、坐标轴(UI Axes)等控件组成。

3.2 系统需求分析

牵引电机滚动轴承可靠性评估系统设计的主要目的是对轨道车辆牵引电机滚动轴承在特定轨道工作环境下运行状态和可靠性进行评估，从而辅助相关的维修人员和技术专家了解特定状态下的滚动轴承的运行状态，为转向架牵引电机滚动轴承的维修和更换提供理论支撑和保障。本模块需要设计的功能主要包括以下几点：

(1)数据存储管理功能。在对牵引电机滚动轴承进行特定时间或者全寿命振动数据采集时，通常都是几千次采集的振动数据。对原始振动数据进行存储和管理，要保证分析和处理后的结果能够被有效地保存。数据存储格式通用性要求较高，一般保存为通用的文本格式，以便能兼容其它专业分析处理软件。分析处理结果的存储必须清晰明朗，数据具有较高的安全性；

(2)数据分析与处理功能。可靠性评估过程涉及的步骤较多，包括特征指标提取和融合、待估参数的求解以及可靠度的计算。为保证处理计算效率高等要求，其中涉及到的算法必须要有较高的处理速度和精确度，才能保证模块的实时性和准确性等要求；

(3)人机交互功能。模块要求功能界面友好，人机交互方便，操作简便易上手，数据处理和分析结果能够直观地在屏幕上显示，便于用户分析和处理。

3.3 系统模块设计

系统模块设计的总体方案如图3所示。

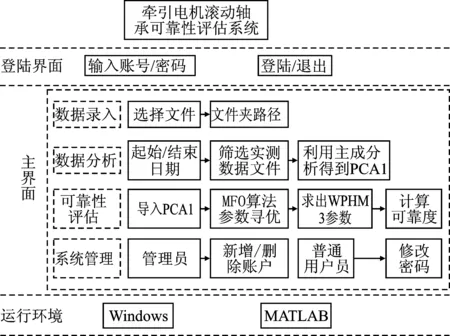
图3 系统模块设计总体方案图Figure 3. Overall scheme of system module design

3.3.1 数据录入模块

数据录入模块主要录入采集的牵引电机滚动轴承振动数据。拖动“选择文件”按钮和“文件夹路径”文本编辑框控件，选中按钮，在右侧“回调”中使用回调函数filepath(·)来实现数据录入功能。

3.3.2数据分析模块

对录入的数据根据实测数据的起始时间和终止时间进行筛选。选择筛选后的数据进行PCA主成分分析，提取第一主成分PCA1。拖动“起始日期”、“终止日期”日期选择控件、“序号/文件名”表控件、“数据分析结果”坐标轴区、“选择数据”和“数据分析”按钮控件。选中“选择数据”按钮，在右侧“回调”中使用回调函数datachoose(·)实现数据选择功能。选中列表中序号对应的一组滚动轴承数据，再选中“数据分析”按钮，在右侧“回调”中使用回调函数pca_analysis(·)，坐标轴中得到主成分分析后的PCA1结果。

3.3.3 可靠性评估模块

将PCA1作为WPHM的响应协变量Z，根据飞蛾扑火优化算法求解WPHM模型参数，计算出可靠度。拖动“可靠性评估”坐标轴、“评估”控件，选中“评估”按钮，在右侧“回调”中使用回调函数reliablity_calculate(·)，嵌套MFO(·)函数，求解出WPHM的β、η、α，计算出可靠度从而完成可靠性评估。

3.3.4 系统管理模块

管理员可指定牵引电机滚动轴承相关负责人和工作用户，并建立账户和密码。普通用户登录系统后可以修改密码，或者通过管理员修改密码。创建一块面板，拖动“账户”、“密码”文本编辑框、“登录”和“退出”按钮。管理员登录进入系统后可以新增或删除账户，点击“登录”按钮，在右侧“回调”中使用回调函数Login(·)，点击“退出”按钮，在右侧“回调”中使用回调函数Out(·)。用户的输入/输出信息始终与Excel相连，并由Excel存储用户信息。系统功能模块对应的流程如图4所示。

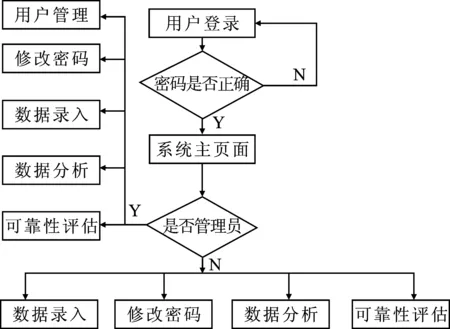
图4 系统功能模块流程图Figure 4. Flow chart of system function module

4 系统实例测试

4.1 实验数据样本来源

本文采用一种基于轮轨分离状态下的转向架牵引电机滚动轴承实车检测方法(如图5所示)，在轨道车辆停运返回车库后对转向架牵引电机滚动轴承进行振动信号采集。首先顶起轮对，使轮轨分离，驱动轮对以不同的转速旋转，再通过数据采集系统采集牵引电机滚动轴承振动信号。此方法有效地避免了轨道车辆在线运行时轮轨激励干扰以及其他部位振源的干扰，降低了噪声的影响，提高了信号的采集质量。图5中的牵引电机滚动轴承为牵引电机驱动端深沟球轴承，型号为SKF6016，传感器为三向振动加速度传感器，通过磁吸座的方式吸附在牵引电机驱动端轴承的正下方。本文中，采样频率为10 240 Hz，采集时间为60 s，每组数据中的数据长度为1 024个采样点，分600组数据。

图5 牵引电机滚动轴承的振动信号采集方案图Figure 5. Vibration signal acquisition scheme diagram of traction motor rolling bearing

4.2 可靠性评估功能实现

点击“选择文件夹”按钮，将牵引电机滚动轴承实测数据录入到系统中，如图6所示。

图6 数据录入图Figure 6. Data entry diagram

在“数据分析”界面指定起始日期和结束日期，点击“选择数据”按钮，右上角表中筛选出多个数据文件。选择序号1，点击“数据分析”按钮，对应轴承1的PCA第一主成分PCA1结果，如图7所示。结合数据分析界面的PCA1结果，点击可靠性评估界面的“评估”按钮，得到拟合后的轴承1可靠度曲线，如图8所示。

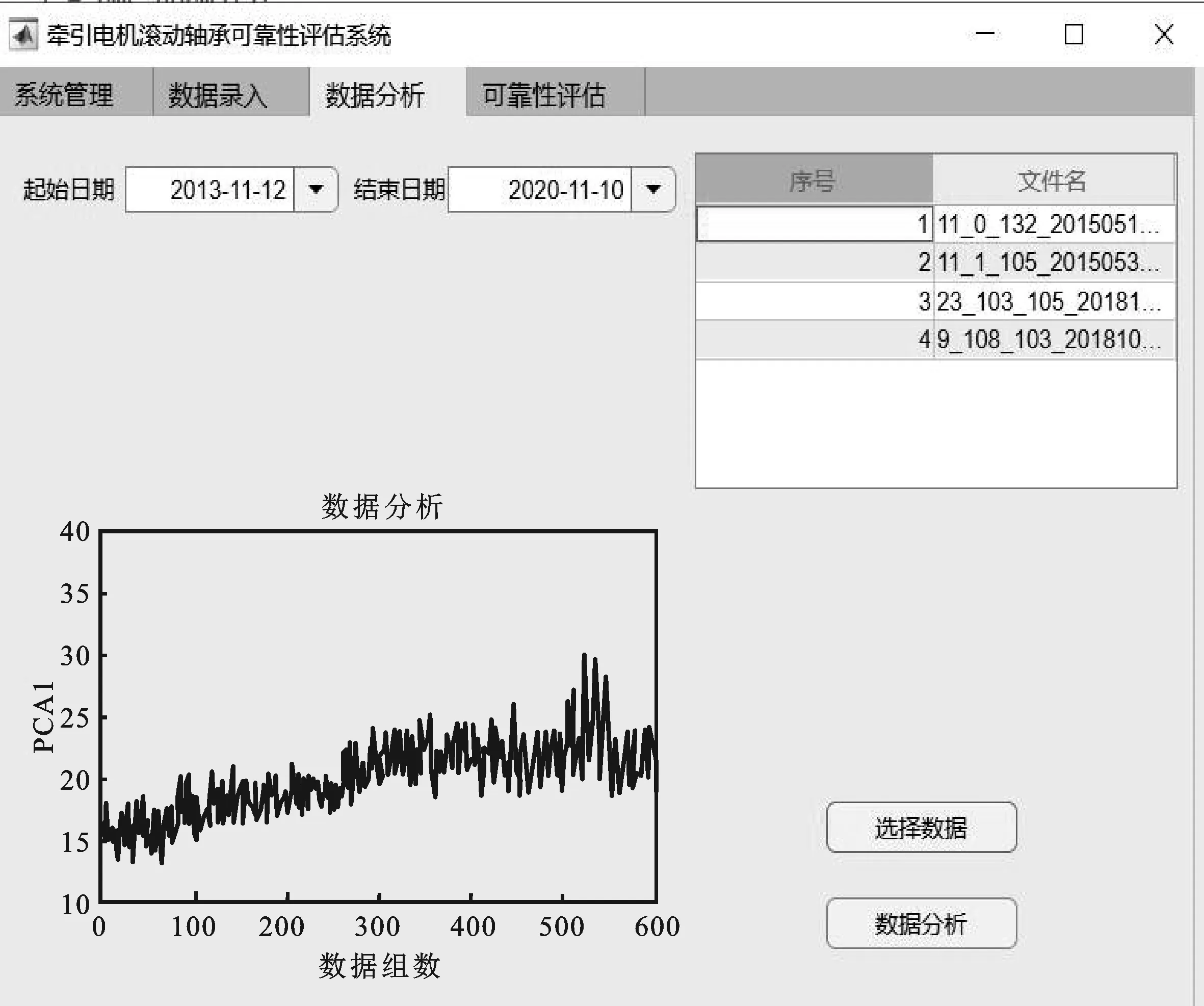
图7 轴承1数据分析结果图Figure 7.Bearing 1 data analysis result

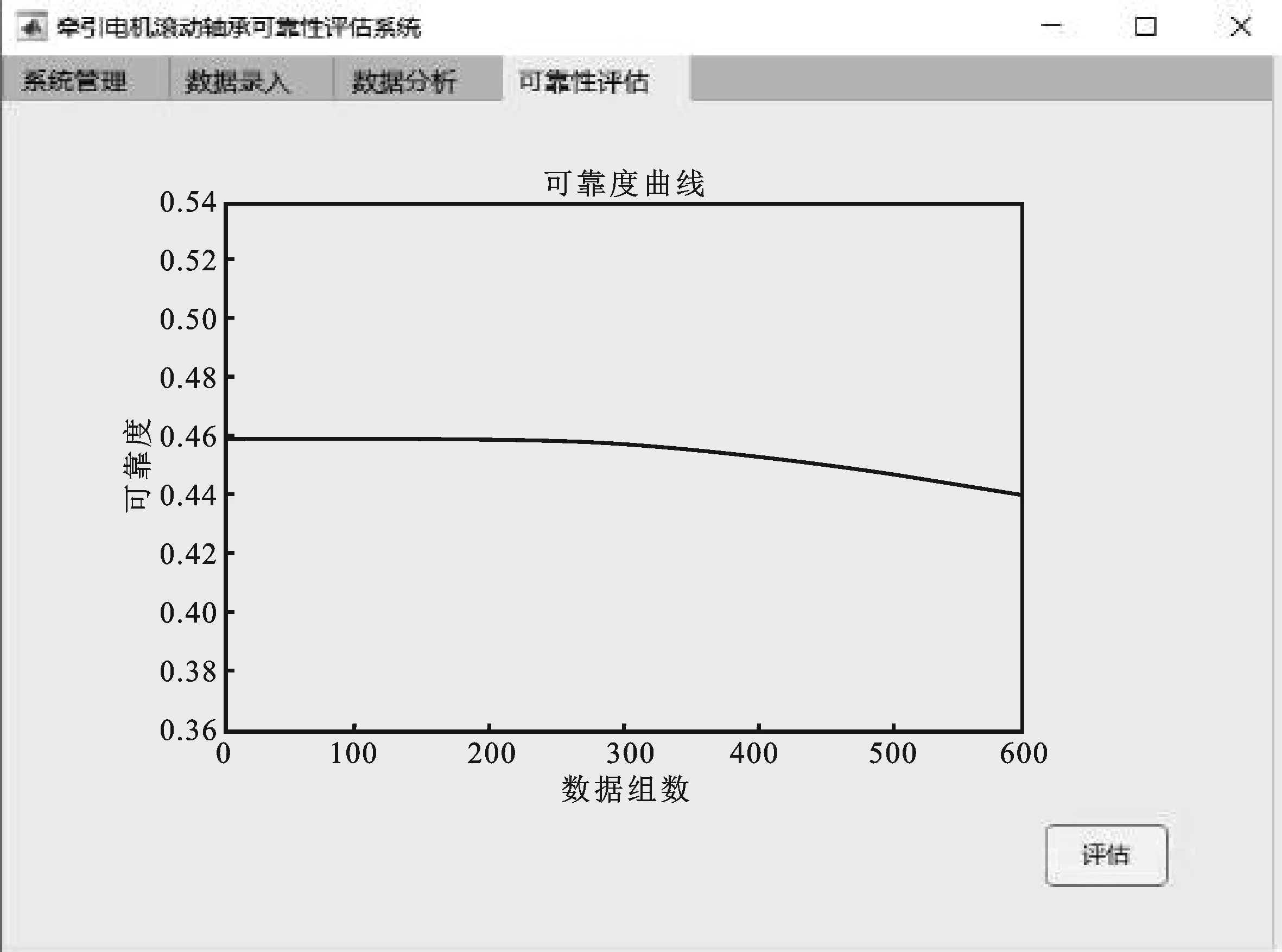
图8 轴承1可靠度曲线图Figure 8.Bearing 1 reliability curve

同理，选择序号2，点击“数据分析”按钮。对应轴承2的PCA第一主成分PCA1结果如图9所示。结合数据分析界面的PCA1结果，点击可靠性评估界面的“评估”按钮，得到拟合后的轴承2可靠度曲线，如图10所示。

图9 轴承2数据分析结果图Figure 9.Bearing 2 data analysis result

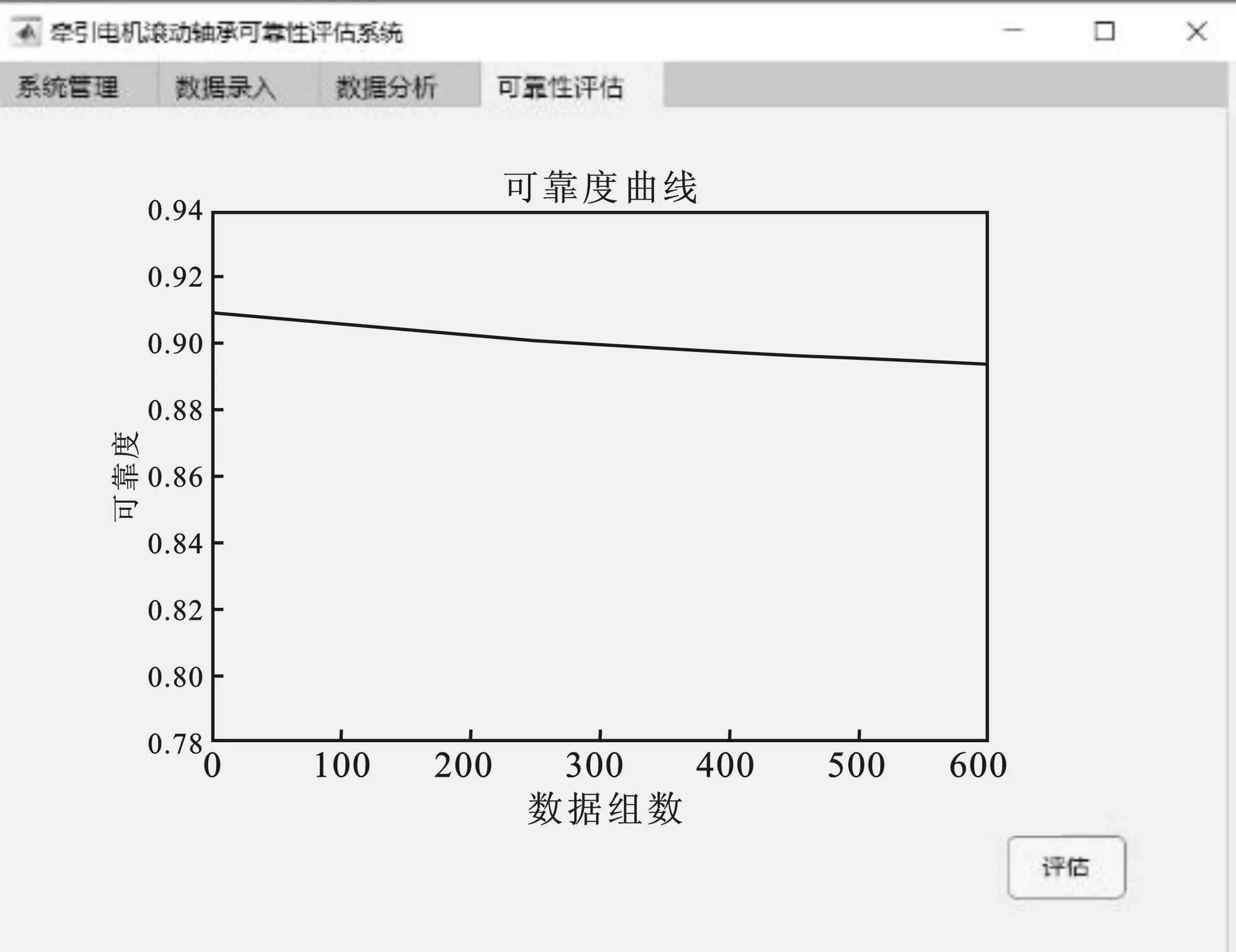
图10 轴承2可靠度曲线图Figure 10.Bearing 2 reliability curve

从图7可知，在400点左右特征指标有一个明显的波动。对应图8的可靠度曲线可以看出，牵引电机滚动轴承可靠性评估模块计算可靠度在0.45左右，400点以后对应的可靠度逐渐减小。通过对牵引电机滚动轴承的拆卸分析可知，牵引电机滚动轴承1的外圈出现了严重烧伤擦伤现象，如图11所示，实际结果与本文方法所求的结果大致吻合。

图11 牵引电机滚动轴承1实际图Figure 11.Traction motor rolling bearing 1 actual picture

从图10可以看出，牵引电机滚动轴承可靠性评估模块计算出的可靠度约为0.9，实际拆卸的滚动轴承2并没有出现故障，可靠度计算结果与实际情况下滚动轴承的状态是相符的。因此，上述结果证明了本文系统设计的有效性。

4.3 用户登陆功能实现

系统用户登录界面如图12所示。

图12 登录界面Figure 12. Login interface

输入账户和密码后，点击登陆按钮，验证身份信息后，系统提示“登陆成功”消息，用户进入系统可以录入牵引电机滚动轴承数据。随后，对数据进行分析，计算出可靠度，完成滚动轴承的可靠性评估。

5 结束语

本文基于MATLAB App Designer设计了一种牵引电机滚动轴承可靠性评估系统。该系统基本实现了牵引电机滚动轴承实测数据的处理，包括数据录入、数据分析和可靠性评估功能。该系统借助MATLAB强大的数学运算能力，不仅展现出良好的滚动轴承可靠性评估效果，而且系统的界面友好、易于操作，且可转化为exe格式的可执行文件，也可脱离MATLAB环境运行，为后续可靠性评估系统研究提供了参考。但是本文所设计系统的可靠度计算进程较为缓慢，模块的交互页面仍需要改善，后续研究将进一步提高算法的计算效率。