基于反步法的四旋翼无人机自适应控制研究

沈昕格，金 海，郭 亮

(浙江理工大学 信息学院,浙江 杭州 310018)

近年来四旋翼无人机由于其具有机身质量轻、结构小、低损耗、易于操控以及可适合复杂飞行环境等优势，被广泛运用于低空巡航、农作物灭火、地图测绘、交通监视、搜索营救等领域[1]。由于四旋翼飞行器是一个典型的多输入多输出、非线性、强耦合的欠驱动系统[2]，且对干扰比较敏感，因此控制难度较大，飞行控制统的设计也较为困难[3]。目前，四旋翼无人机的飞行控制已成为国内外研究者重点研究的课题。线性控制中的PID(Proportion Integration Derivative)控制结构简单，参数易整定，对被控对象精确度要求不高，且可保证一定的鲁棒性[4]。然而在外界干扰较多的情况下，该方法无法有效地使无人机保持稳定[5]。LQR(Linear Quadratic Regulator)控制也属于线性控制，可得到状态线性反馈的最优控制规律，易构成闭环最优控制[6]，但是其控制效果会受到模型准确度低的影响。

线性控制模型过于简单，忽略了很多重要因素，导致实际飞行中控制效果并不理想，针对该问题研究人员提出一系列非线性控制方法[7]。滑模控制能够实现无人机稳定跟踪，但其忽略了不确定的影响[8]。传统反步法控制可以处理大多数不确定因素的影响，但在实际应用中，传统反步法的抗干扰能力不足[9]。为解决上述问题，本文提出了基于反步法的自适应控制系统。

1 四旋翼无人机的动力学建模

为了建立四旋翼飞行器的数学模型，本文做出以下假设：(1)飞行器为刚体的并且严格对称，质量不变；(2)重力加速度不随飞行高度的变化而变化；(3)机体坐标系原点位于机体几何中心处；(4)飞行器的每个旋翼产生的升力与旋翼的转速成正比。

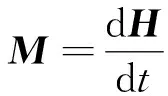
(1)

式中，b为升力系数；w为转子转速；l表示旋翼中心到机体质心的距离；d表示旋翼的阻力系数。

Md可以表示为

(2)

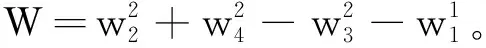
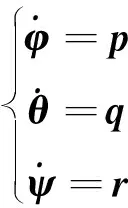
(3)

定义4个控制通道的控制输入，则有

(4)

考虑到无人机的飞行结构和特点，为设计控制器方便，忽略飞行过程中的陀螺效应以及空气阻力对四旋翼飞行器的影响，将无人机动力学模型进行简化[13]，得到

(5)

其中，Ix、Iy、Iz可以表示飞行器绕OXb、OYb、OZb轴的转动惯量；缩写S(·)、C(·)和T(·)分别表示sin(·)、cos(·)和tan(·)。

2 反步法控制器设计

2.1 模型变换

四旋翼无人机模型含有4个控制输入和6个状态输出，是一个强耦合、欠驱动的系统[14]。当考虑加入执行器的故障Di时，可将四旋翼动力学方程式为

(6)

(7)

2.2 控制策略

根据动力学模型可知，四旋翼无人飞行器的控制系统分为姿态环和位置环[15]。设期望位置输入为 (xd,yd,zd)，期望姿态输入为 (φd,θd,ψd)。在位置环由期望位置输入与无人机实际位置作差，设计出位置控制器U1、Ux和Uy[16]。进入到姿态内环后，由Ux和Uy反解得到期望的姿态角，最后将其与实际姿态角作差就可以得到控制器U2、U3和U4[17]。控制结构框图如图1所示。

图1 四旋翼无人机控制结构框图Figure 1. Block diagram of the control structure of a quadrotor UAV

2.3 姿态控制回路控制器设计

滚转角子系统可以表示为

(8)

设期望滚转角φd=x1d，令滚转角的跟踪误差为

e1=x1d-x1

(9)

对其求导可得

(10)

选取Lyapunov函数

(11)

对其求导可得

(12)

其中，α1为引入的虚拟控制量

(13)

e2为x2的误差信号

e2=x2-α1

(14)

将式(13)代入式(12)得

(15)

由式(10)、式(13)和式(14)可得

(16)

(17)

为设计实际控制输入U2，取Lyapunov函数

(18)

对其求导并将式(13)和式(14)代入可得

(19)

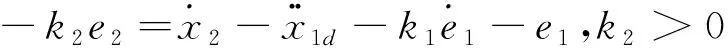
(20)

则式(19)可写为

(21)

由式(8)解得U2，并将式(16)和式(20)代入可得

(22)

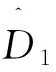
(23)

对式(23)求导可得

(24)

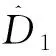
(25)

则根据Lyapunov稳定性理论，该系统渐近稳定。所以得到式(26)。

(26)

同理，根据控制输入U2的设计过程，可以设计俯仰通道控制量U3和偏航通道控制量U4。

经过推导可得

(27)

(28)

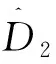
(29)

(30)

2.4 位置控制回路控制器设计

高度子系统为

(31)

设置高度值zd=x11d，令跟踪误差e11=x11d-x11。

选取Lyapunov函数

(32)

并令D4估计值的自适应律为

(33)

则根据Lyapunov稳定性理论，该系统渐近稳定。所以得到

(34)

同理，可分别求得x和y通道的控制输入Ux、Uy

(35)

(36)

2.5 滚转角和俯仰角期望值的反解

由四旋翼无人机的动力学模型可知，滚转、俯仰通道和其水平控制通道有紧密联系。进而可以得到如下的等价关系

(37)

则由ψd=x5d，e5=x5d-x5和式(38)可反解得期望的滚转角和俯仰角

(38)

由控制量反解得到期望的姿态角后，就能将控制系统的内环和外环完整的连接起来[18-19]。

3 系统仿真分析

通过MATLAB进行数值仿真来验证在外界干扰的情况下，所设计系统的抗干扰能力。

仿真中，设期望偏航角ψd=0 rad时初始位置(x,y,z)=0 m，期望位置(xd,yd,zd)=(1,1,1) m，在t=10 s时加入外界干扰信号，仿真时间为T=40 s，模型参数如表1所示。

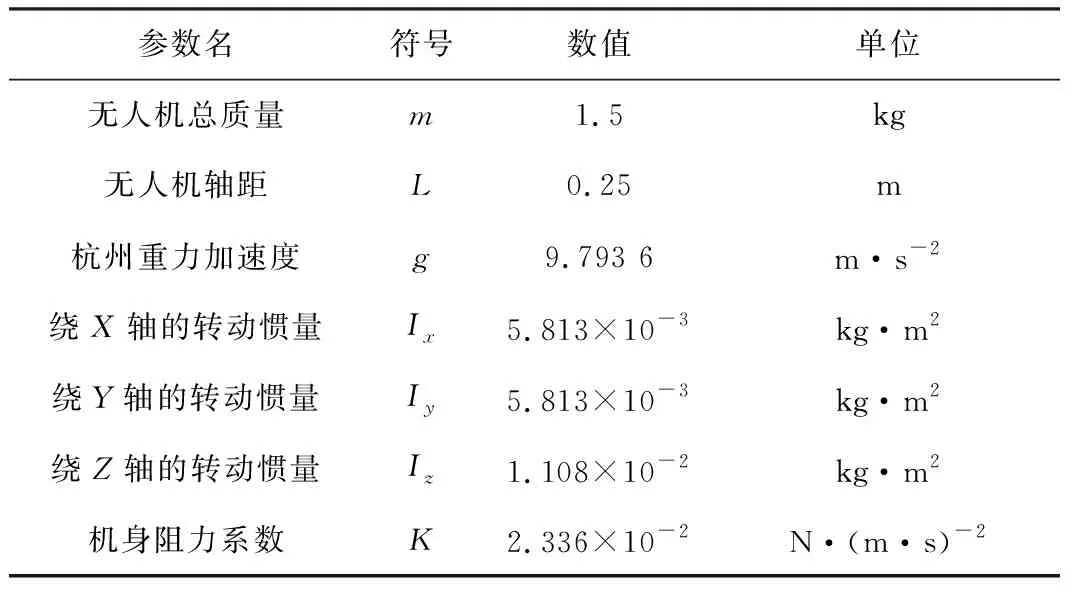
表1 无人机数学仿真模型参数

在自适应反步法控制下的姿态角跟踪曲线如图2～图4所示。

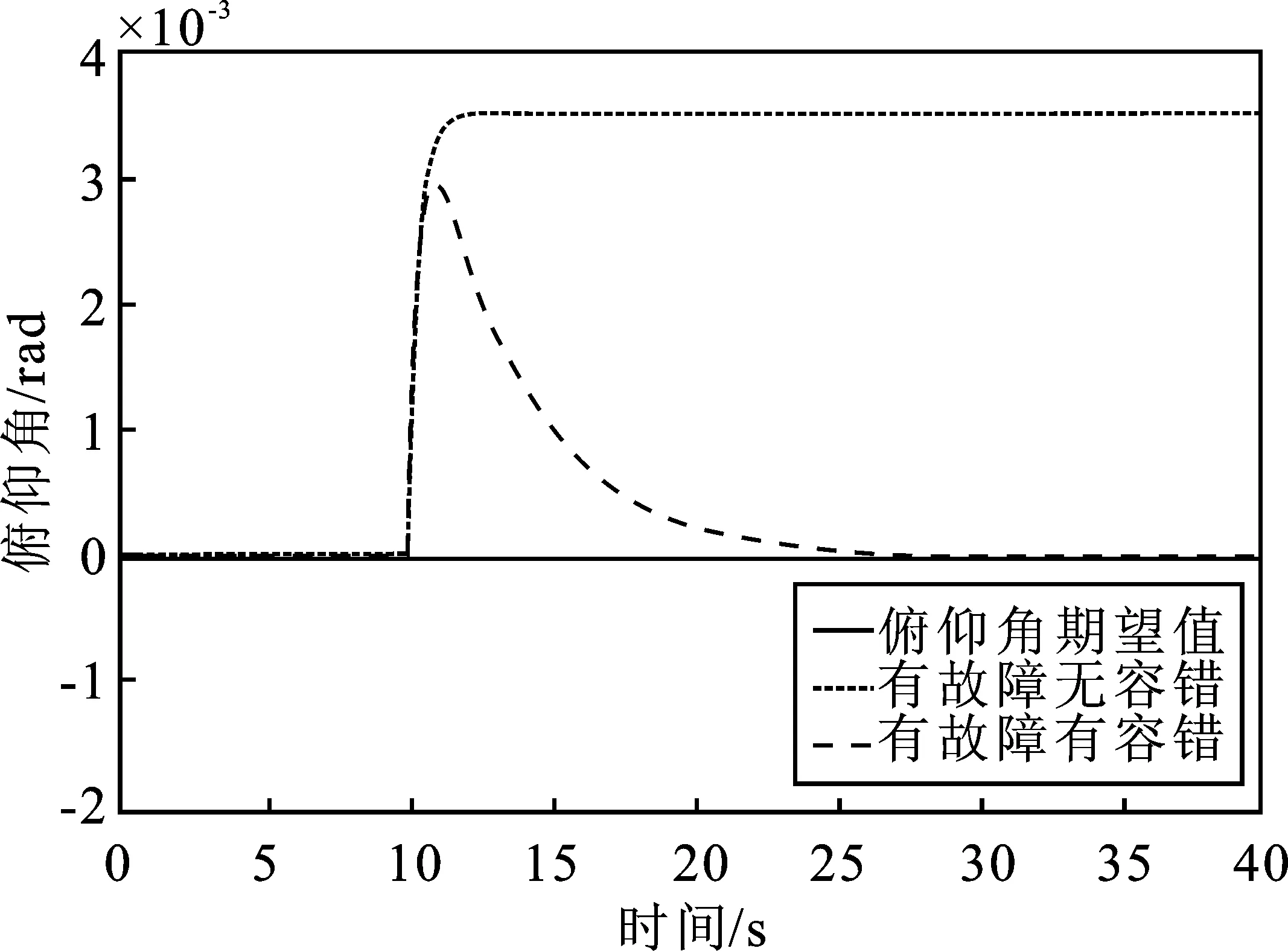
图2 干扰下的俯仰角跟踪曲线Figure 2. Pitch angle tracking curve under interference

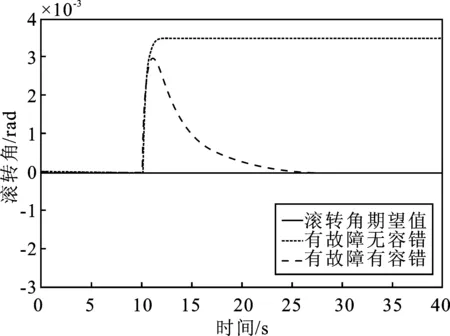
图3 干扰下的滚转角跟踪曲线Figure 3. Roll angle tracking curve under interference

图4 干扰下的偏航角跟踪曲线Figure 4. Yaw angle tracking curve under interference

由图2～图4的姿态跟踪曲线可以看出，在10 s处加入干扰信号后，未加入抗干扰功能的姿态曲线迅速偏离轨道，并无法自我调节到期望角度。使用反步法自适应控制器的无人机由于具有容错功能，在外界干扰情况下，翻滚和俯仰曲线能在15 s内稳定到原有的期望状态(如图2和图3所示)，且不存在超调现象，此时偏航角的最大误差仅为0.000 8，证明其具有良好的动态特性和静态特性。

在自适应反步法控制下的无人机位置仿真结果如图5～图7所示。

图5 干扰下的X轴跟踪曲线Figure 5.X-axis tracking curve under interference

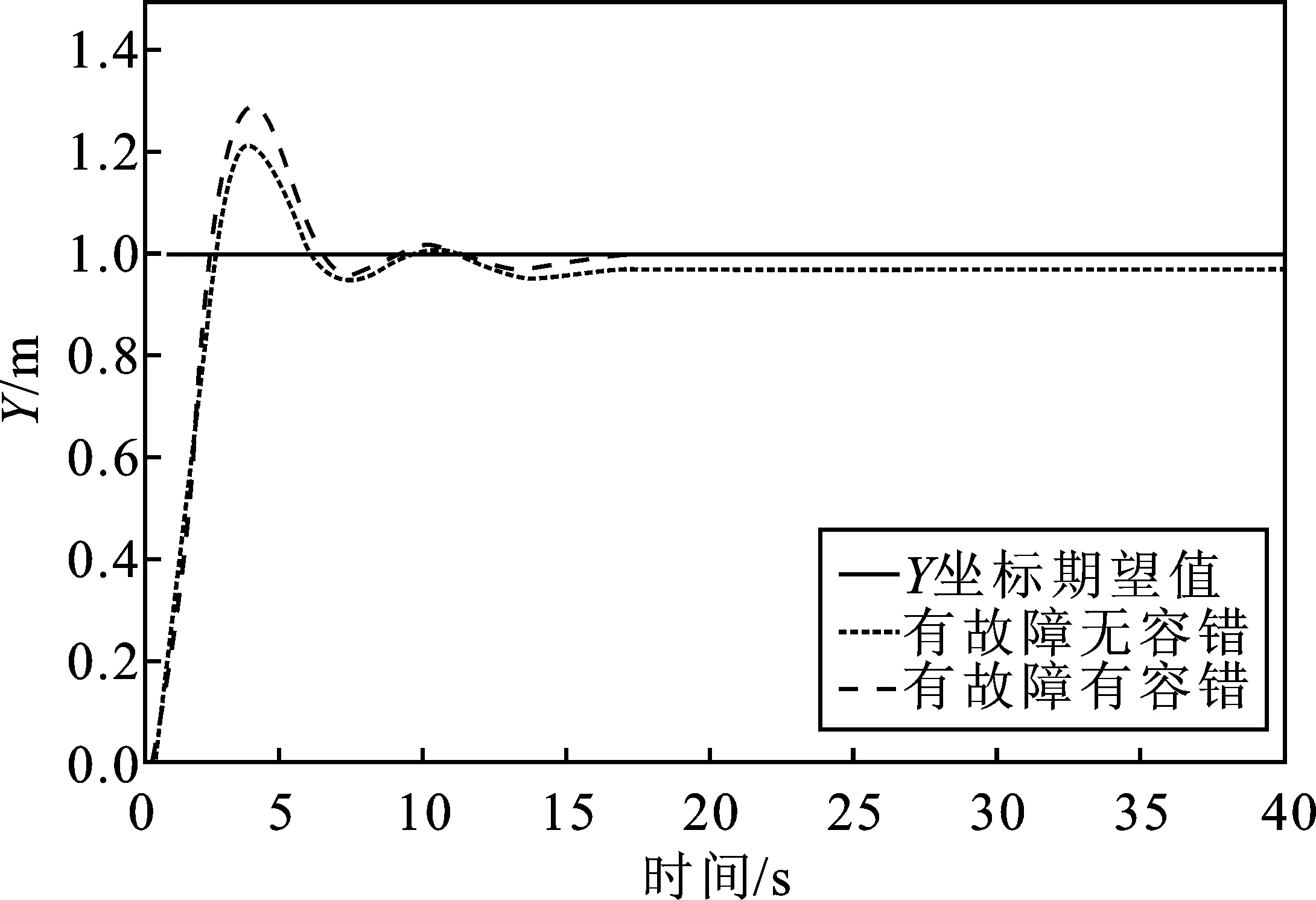
图6 干扰下的Y轴跟踪曲线Figure 6. Y-axis tracking curve under interference

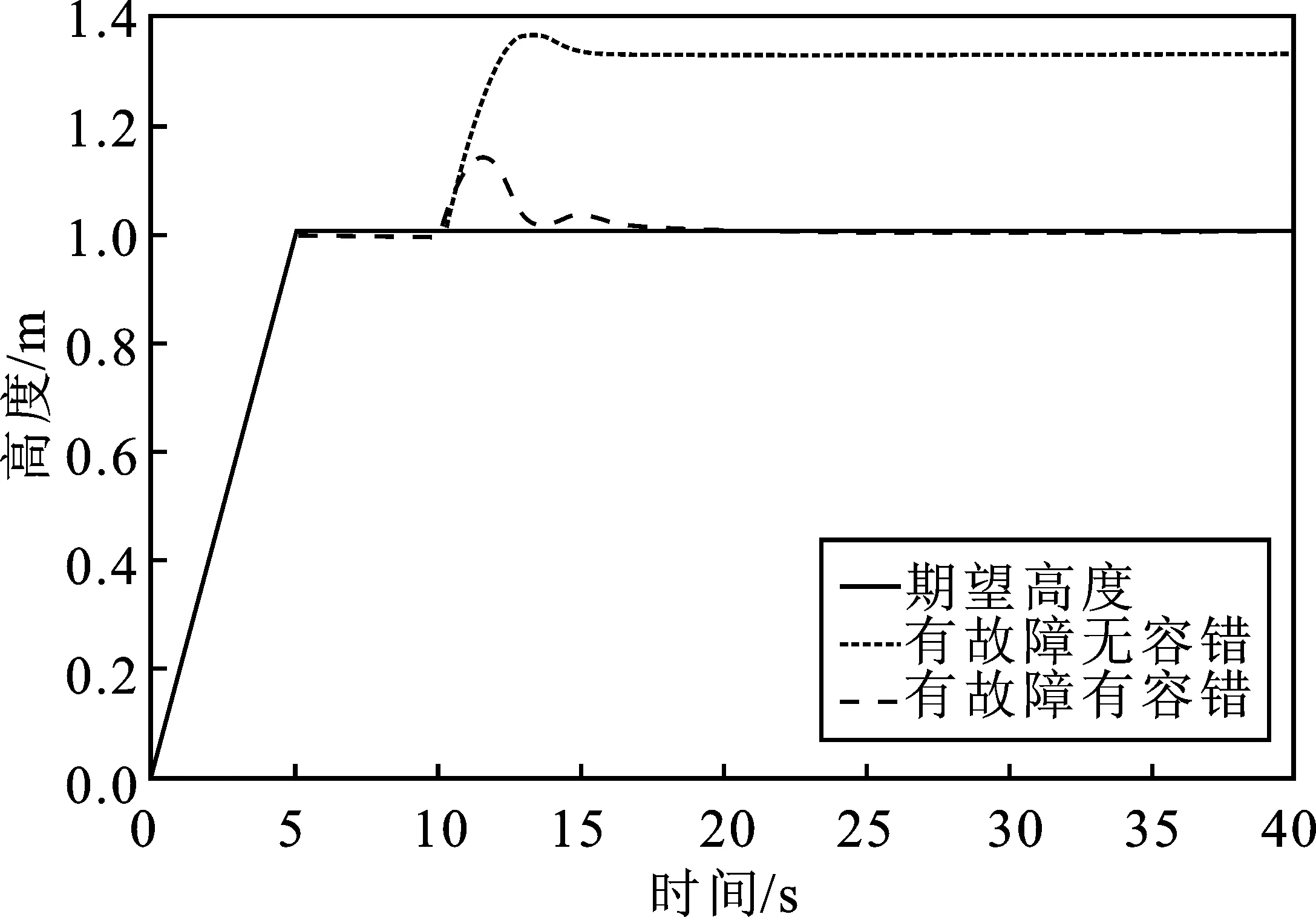
图7 干扰下的高度跟踪曲线Figure 7. Height tracking curve under interference

由图5～图7的位置跟踪曲线可以得出，位置跟踪曲线在干扰信号的影响下，输出响应在一开始有轻微超调现象，但其能够在7 s内快速稳定在1 m附近，静态误差较小，仅为0.000 7。相比之下，未加入抗干扰功能的位置曲线偏离期望位置，无法进行位置调节。

4 结束语

为解决无人机在外界干扰下的稳定性问题，本文运用了反步法并结合自适应控制设计了基于反步法的自适应控制器，并通过MATLAB-Simulink仿真证明该系统能够解决四旋翼无人机在外界干扰情况下的位置和姿态稳定性问题。该控制器能够使无人机在干扰环境下迅速达到期望的位置和姿态稳定状态，并具有良好的静态特性和动态特性。然而，此方法在现阶段暂未用在四旋翼无人机的稳定性实验中，相关结果还有待进一步验证。