单相无刷直流电机的设计分析与建模仿真

上官璇峰,杨婷玉,卫劲松,刘永健

(河南理工大学 电气工程与自动化学院,河南 焦作 454000)

与三相无刷直流电机相比，单相无刷直流电机效率低，响应迟滞。但单相无刷直流电机的结构和制造工艺较简单，成本较低，因此被广泛应用于低成本、低起动转矩和对电机性能要求不太高的小功率设备中，例如小功率风机和水泵[1-4]。

对称结构的单相无刷直流电机齿槽转矩过零点位置和电磁转矩零点位置重合，转子静止于这些位置时，电机通电后无法正常起动[5]。为了解决“起动死点”问题，单相无刷直流电机通常采用不对称气隙结构，使齿槽转矩过零点位置偏离电磁转矩的零点位置，从而使转子获得一定的起动转矩。但是不均匀气隙会引起转矩脉动，增加电机振动和噪声，影响电机性能[6-9]。文献[10]分析了4种不均匀气隙方案电机的性能，证明锥形渐变气隙性能最优，但仍存在较大的转矩脉动。文献[11]针对锥形渐变气隙电机的定子形状优化，提出定子开槽结构。新结构的电机有效降低了转矩脉动，但没有分析控制方式对电机性能的影响。文献[12]提出了一种参考电压PWM控制技术，有效削弱了转矩脉动。近年来，国内外学者针对解决起动死点问题和抑制转矩脉动方面做了大量研究，在电机本体结构和控制策略方面取得了一定的成果。但是对于单相无刷直流电机本体设计的研究较少，目前仍缺乏一套完整的设计理论。单相无刷直流电机的磁场分布相对复杂，很难用简单的表达式表达反电动势和齿槽转矩[13]，给电机设计和性能分析带来了困难。

本文在介绍单相无刷直流电机拓扑结构特点的基础上，推导了单相无刷直流电机理想工况下的基本方程，并根据功率方程推导出电机的参数方程，确定了电机主要尺寸[14-16]。本文通过建立有限元模型对所设计电机的基本电磁特性仿真分析，在Simulink环境中搭建了单相无刷直流电机开环控制系统的模型[17]，仿真得到电机的转速、转矩变化曲线。仿真结果与理论分析较为一致，进一步验证了电机设计方案的合理性。本文总结的设计流程对该类型的电机设计具有一定的参考价值，在Simulink环境中搭建的电机模型为分析设计单相无刷直流电机提供了有效方便的方法。

1 电机结构和工作原理

单相无刷直流电机用电子换相装置取代了传统有刷直流电机的电刷和换相片，可提高电机运行转速和可靠性，降低电磁干扰，延长使用寿命[18]。单相无刷直流电机的拓扑结构如图1所示。

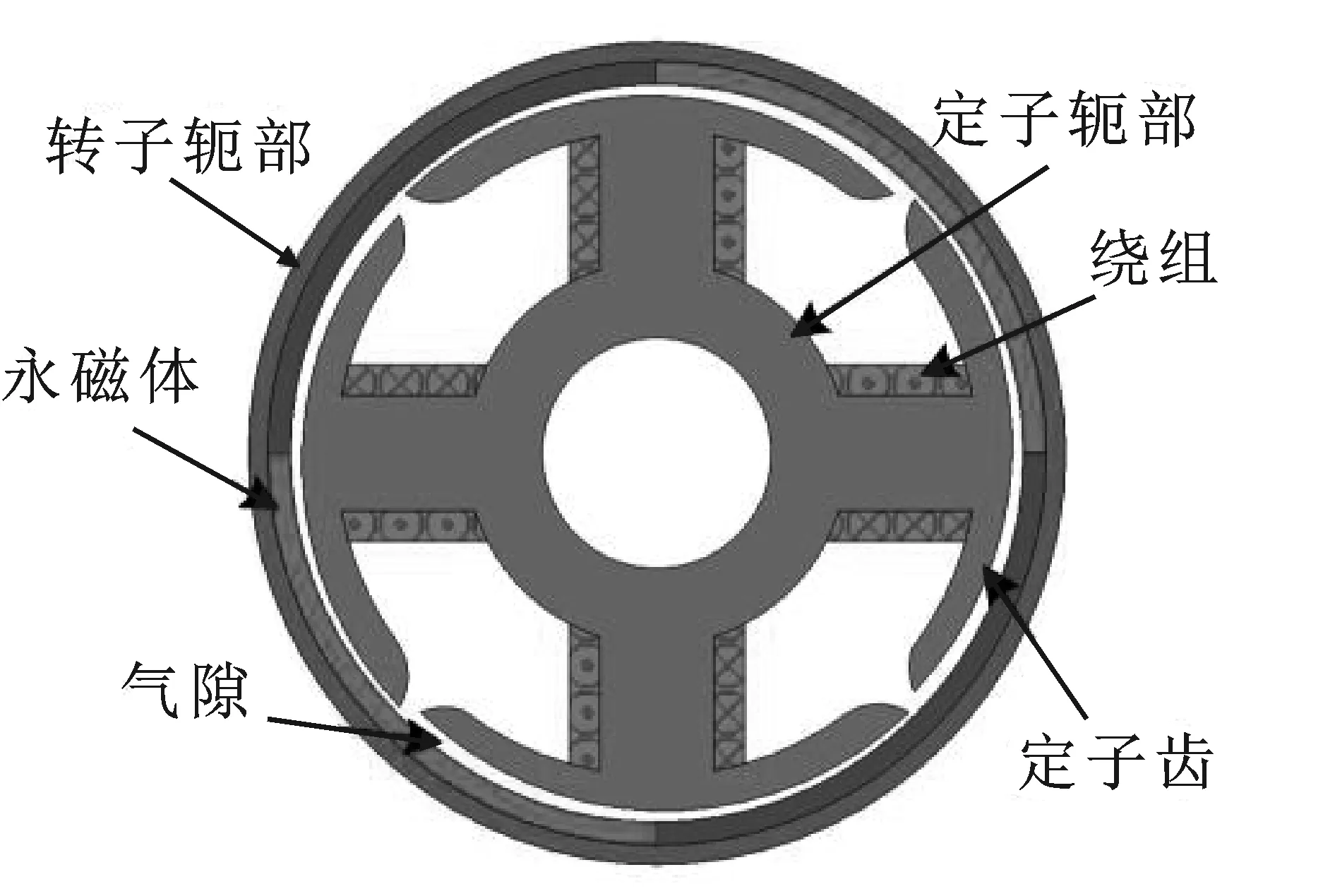
图1 外转子单相无刷直流电机拓扑结构Figure 1. Topological structure of brushless DC motor with external rotor

电机本体由定子和转子两部分组成，转子上的永磁体通常为整体式，且其磁极对数与定子凸极对数相等。电机定转子极面间采用锥形渐变气隙，使齿槽转矩过零点与电磁转矩零点不重合，克服了起动死点问题。由于定子使用直流电源给绕组供电，只能产生固定的定子磁场，而转子磁场随转子位置变化而改变，因此定转子磁场间位置不断改变。同步改变定子磁场方向，使定转子磁场间夹角始终保持在0°～180°电角度，保证电磁转矩方向不变，从而驱动电机连续单向旋转。

2 电机设计

2.1 主要参数的确定

电机初始设计要求如表1所示。

表1 电机初始设计要求

空载运行时反电势E0可表示为

(1)

式中，N为绕组匝数；ω为机械角速度；θ为转子位置角；φ为永磁磁通，可定义为

φ=φmcos(Prθ)=kdkFατlBδm

(2)

式中，φm为永磁磁通幅值；Pr为转子极数；Ps为定子槽数；kd为漏磁系数；kF为气隙磁密分布系数；Bδm为气隙磁密幅值；α为极弧系数；Dso为定子外径；ls为轴向长度。

将式(2)代入式(1)中，空载反电势可表示为

(3)

其中，

(4)

相电流幅值表达式为

(5)

式中，ki为常数；Irms为电流有效值；Dso为定子外径；As为电负荷。

有功功率表达式为

(6)

式中，U1为相电压；I1为相电流；φ为功率因数角；ke为电势常数。

将式(4)和式(5)入式(6)中，得到有功功率表达式

(7)

基于上述分析可得到单相无刷直流电机的输出功率表达式

(8)

式中，η为效率。

根据式(8)得到电机结构参数方程，如式(9)所示。

(9)

一般情况下kd的取值范围是0.89～0.93，kF的取值范围是1.2～1.8，本次电机额定功率为38 W。参照小功率永磁电机的电负荷取值经验，本文取AS=930 A·m-1，取电机气隙磁密幅值Bδm=0.25 T。

将以上选取的参数值带入式(9)可得

Dso2ls=2.77×10-4m3

(10)

取长径比λ=0.34，计算得电机定子外径Dso=9.3 cm，电枢轴向长度ls=3.2 cm。

结合所需气隙磁密通过磁路计算选择表贴式结构的永磁体厚度hm，还要考虑抑制最大过流时的去磁能力，故hm的计算式如下[19]

(11)

式中，ks为外磁路饱和系数，取ks=1.3；kδ为气隙系数，取kδ=1.4；Bδ为气隙磁密，取Bδ=0.25 T；δav为平均气隙长度，取δav=0.8 mm；μ0为真空磁导率；H为永磁体的矫顽力，取H=297.8 kA·m-1。

将以上选取的参数值带入式(11)可得式(12)。

hm=2.14 mm

(12)

综合考虑电机的性能和经济性，在该外转子型单相无刷直流电机的设计中，需要通过增加铁氧体厚度来增加气隙磁密，故取hm=3 mm。永磁体结构采用圆筒形，结构简单，加工和装配方便，可降低总成本。

2.2 渐变气隙对齿槽转矩的影响

齿槽转矩是定子齿槽和转子磁势相互作用产生的，属于电机的固有属性，且分布与电机结构有关。齿槽转矩会引起转矩脉动，产生振动和噪声[20]。对于单相无刷直流电机而言，齿槽转矩是电机起动和提高效率的关键。通过优化齿槽转矩波形可提高电机起动转矩，补偿电磁转矩周期性降落，提高输出转矩的目的。图2为两种气隙结构下的齿槽转矩的有限元解。

图2 齿槽转矩对比Figure 2. Comparison of cogging torque

由图2可知，当单相无刷直流电机采用均匀气隙时齿槽转矩过零点在α=45°(磁极中心)的位置，该位置电磁转矩也为零，且在一个极距内产生的齿槽转矩波形正负峰值幅值相等，因此电机静止在此位置时无法起动，称此位置为起动死点。而采用渐变气隙结构，不仅使齿槽转矩过零点位置偏离磁极中心位置，且齿槽转矩波形正峰明显大于负峰。所以与均匀气隙相比，渐变气隙结构使齿槽转矩波形发生畸变，使电机静止时偏离显著提高电机起动性能。本文所设计的电机渐变气隙结构由两个偏心圆形成，如图3所示。

图3 渐变气隙的电机结构Figure 3. Motor structure with gradient air gap

由图3可知，定子表面是一段圆弧，其圆心在偏离原圆心位置一段距离处，该偏离圆心距中心O的距离为X。本文偏移量X分别取0.5 mm、0.8 mm、1.0 mm、1.2 mm、1.5 mm，所对应的齿槽转矩波形如图4所示，所对应的起动转矩如表2所示。

图4 不同偏移量下的齿槽转矩波形Figure 4. Tooth torque waveform under different offsets

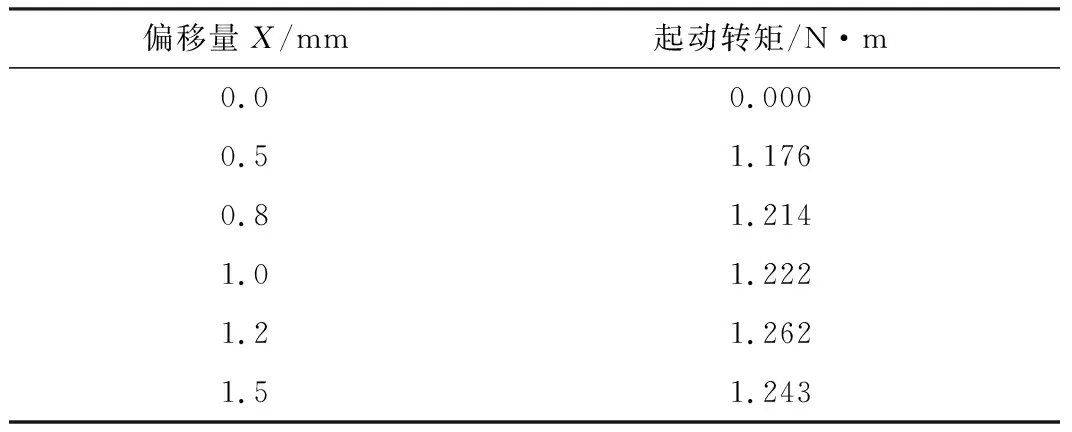
表2 不同偏移量下的起动转矩

由图4可知，随着圆心水平偏移量X的逐渐增加，即气隙不对称程度增加，齿槽转矩峰值逐渐增加。由表2可知，随着偏移量X的增加，起动转矩逐渐增加。当X=1.2 mm时，起动转矩达到峰值，若继续增加偏移量X，起动转矩会减小。这是因为偏移量过大时会减小气隙磁密，降低电机效率，同等功率下电机体积增大，影响电机性能。所以对于本例，X=1.2 mm为临界值，偏移量应小于等于该值。若偏移量过小使加工难度增大，电机性能容易受到影响。故本文取气隙表面圆弧偏移量X=1 mm，此时加工方便电机性能不易受影响。

2.3 绕组的设计

目前单相无刷直流电机常见的绕组方式有单极性连接方式和双极性连接方式[20]。两者在主电路中的拓扑结构分别如图5(a)和图5(b)所示。

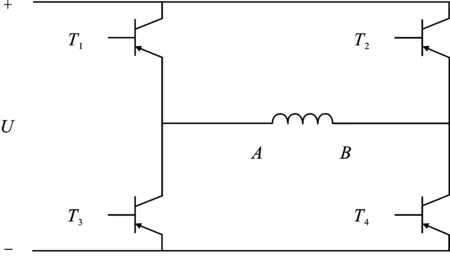
(a)

相比单极性绕组，双极性绕组连接简单，可靠性高，且双极性绕组在每个通电状态下流过相同定子电流时所需绕组匝数是单极性绕组的一半，线圈利用率高，成本低。单极性绕组换向时刻存在续流，使电磁转矩波动变大，增大损耗。因此，本文研究的风机采用双极性绕组连接方式。

2.4 设计方案

综合以上分析，初步得到电机的主要参数如表3所示。电机材料选择如下：定子铁心使用50W270硅钢片，永磁体使用C7铁氧体，转子磁轭使用10号钢，绕组使用线径0.5 mm的铜线。

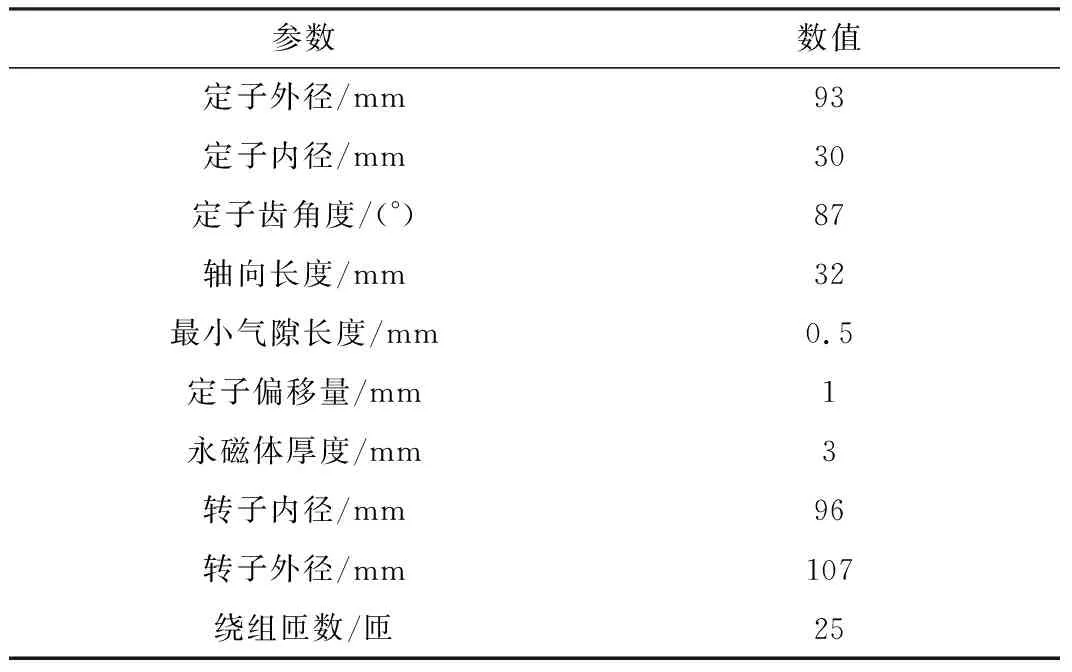
表3 电机主要设计参数

3 仿真分析

3.1 电机有限元建模

为了验证以上理论分析的准确性，通过MagNet软件对该电机进行二维有限元仿真分析。单相无刷直流电机结构模型图、网格剖分图、磁力线分布图、磁场分布云图如图6所示。

图6 有限元模型Figure 6. Finite element model

仿真得到电机的径向气隙磁密波形图如图7所示。

图7 径向气隙磁密波形Figure 7. Radial air gap magnetic density waveform

由图7可得最大气隙磁感应强度为0.21 T，符合初步设计方案。气隙磁密波形对于磁极中心线左右不对称(磁极中心位于图中横坐标45°、135°、225°、315°的位置分别对应A、B、C、D点)，这主要是由气隙不对称和槽的存在导致气隙磁导变化引起的。在额定转速时，仿真得到电机的反电动势波形如图8所示。

由图8可知反电动势波形非理想的平顶波，且近似平顶部分左右不对称，这是由于电机不均匀气隙结构和齿槽转矩引起的磁密波动从而影响反电势波形。有限元仿真结果与理论分析吻合，初步证明电机设计方案的合理性。有限元软件可以更直观的体现电机内部磁场分布情况，能对电机电磁场精确求解计算，但是不利于研究控制系统对电机性能的影响，且求解时间较长。

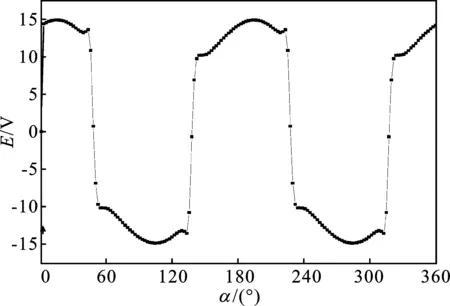
图8 空载时反电动势波形Figure 8. Counter emf waveform at no load

3.2 基于MATLAB/Simulink的电机系统模型

综合上述对单相无刷直流工作原理和数学模型的分析以及从有限元模型中获取的齿槽转矩波形、反电势系数波形，可基于Simulink建立单相无刷直流电机的仿真模型，进一步分析电机的起动特性和控制方式对电机转速、电磁转矩等参数的影响。根据单相无刷直流电机的数学模型，在Simulink中搭建的电机模型如图9所示。

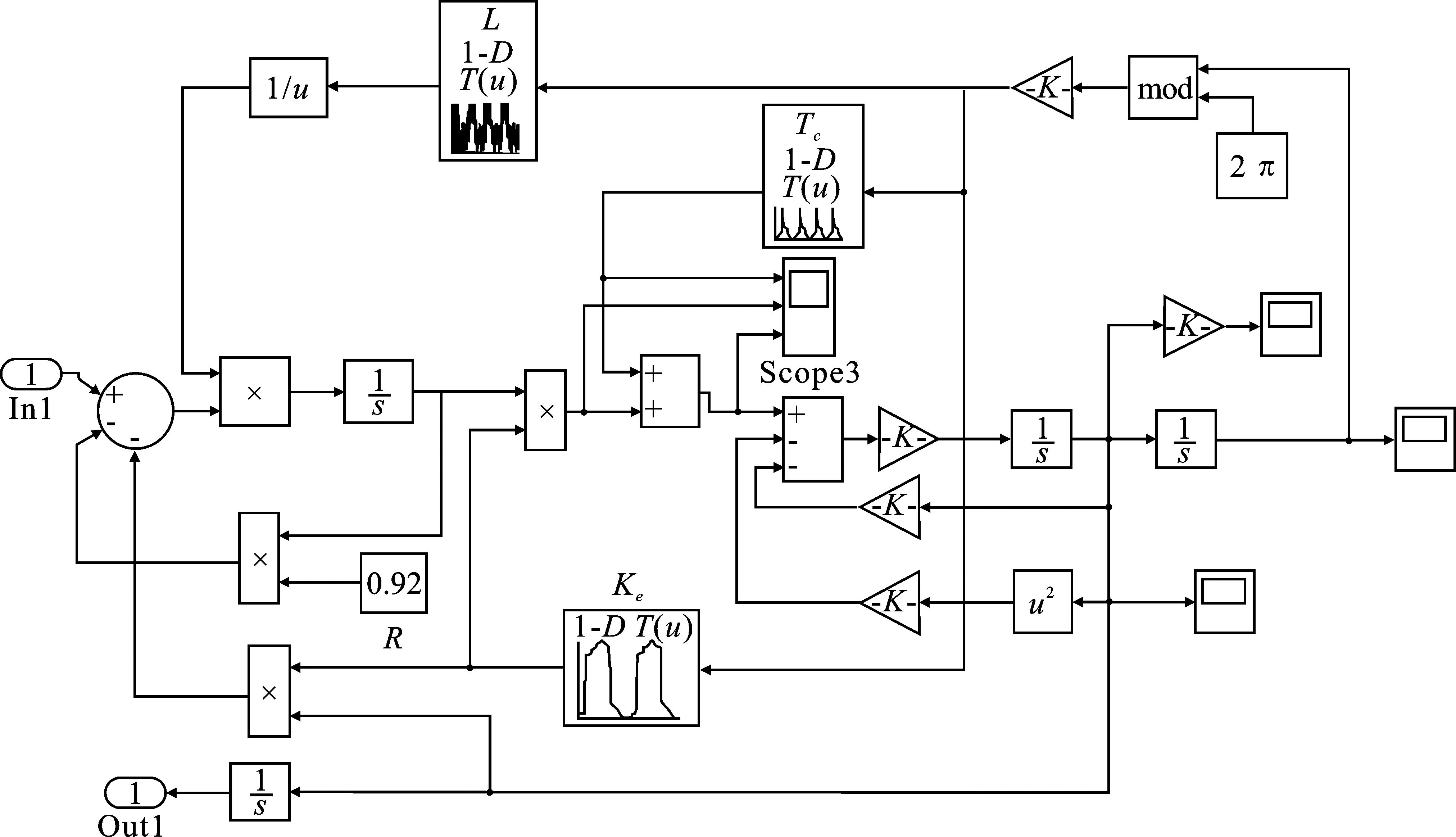
图9 单相无刷直流电机模型Figure 9. Brushless DC motor model

由于模型中的反电动势系数和齿槽转矩均是由转子位置决定的复杂波形，且无法用简单的解析式表达，因此本文在模型中利用了查表(Look-up Tables)模块，从有限元软件中获取数据序列。这样做充分考虑了电机反电动势系数和齿槽转矩相对于转子位置的非线性关系，对实际单相无刷直流电机系统有较高的模拟精度。单相无刷直流电机控制系统采用开环控制策略，无反馈回路，结构简单，成本较低。开环控制模块如图10所示，整个单相无刷直流电机系统模型如图11所示。

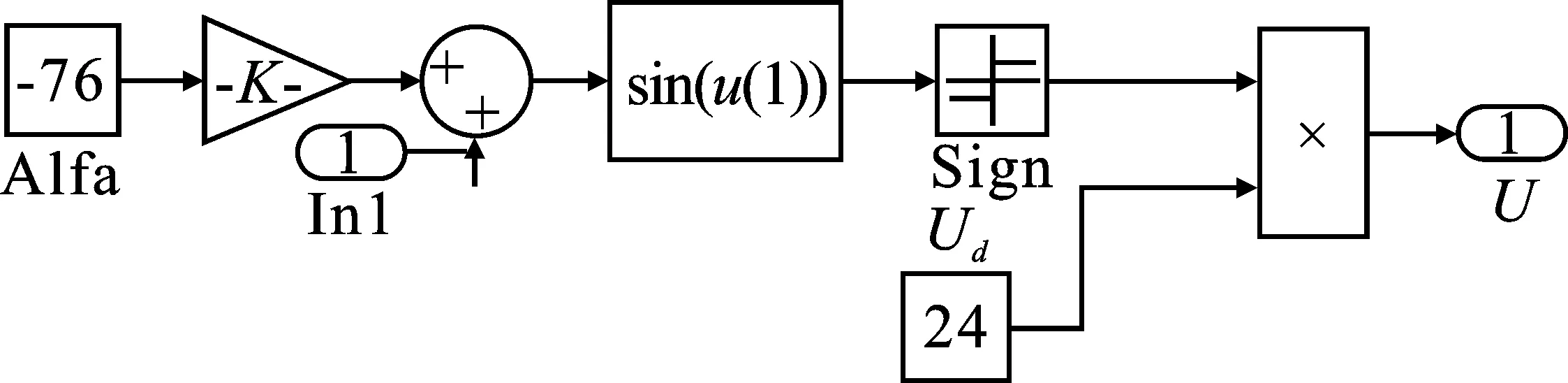
图10 开环控制模型Figure 10. Open-loop control model

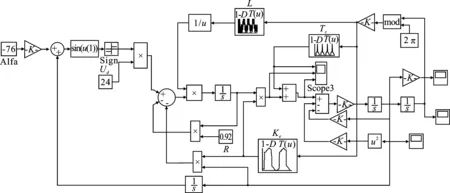
图11 单相无刷直流电机系统模型Figure 11. Brushless DC motor system model

3.3 仿真结果分析

利用Simulink搭建了单相无刷直流电机开环控制系统模型，对各模块参数赋值，并进行了仿真测试。仿真参数设置为：定子绕组电阻R=0.92 Ω，额定转速n=750 r·min-1，转动惯量J= 0.000 56 kg·m2，负载类型为风机类负载，转矩大小与转速平方成正比，即T=kFn2，取kF= 0.000 06。电机空载运行时的转速仿真结果如图12所示，电机带负载运行时的转速仿真结果如图13所示。

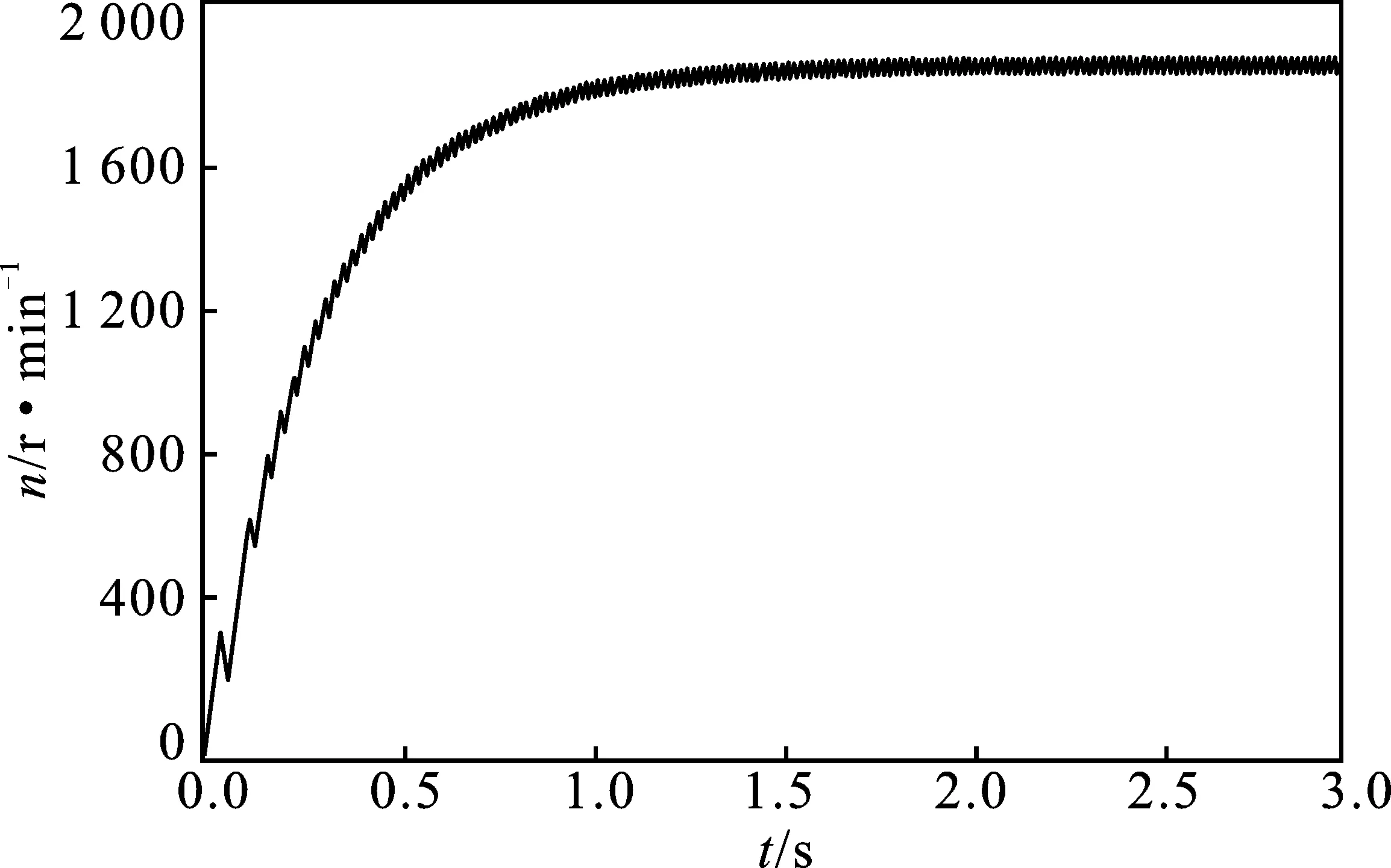
图12 空载时转速响应Figure 12. Speed response under no load

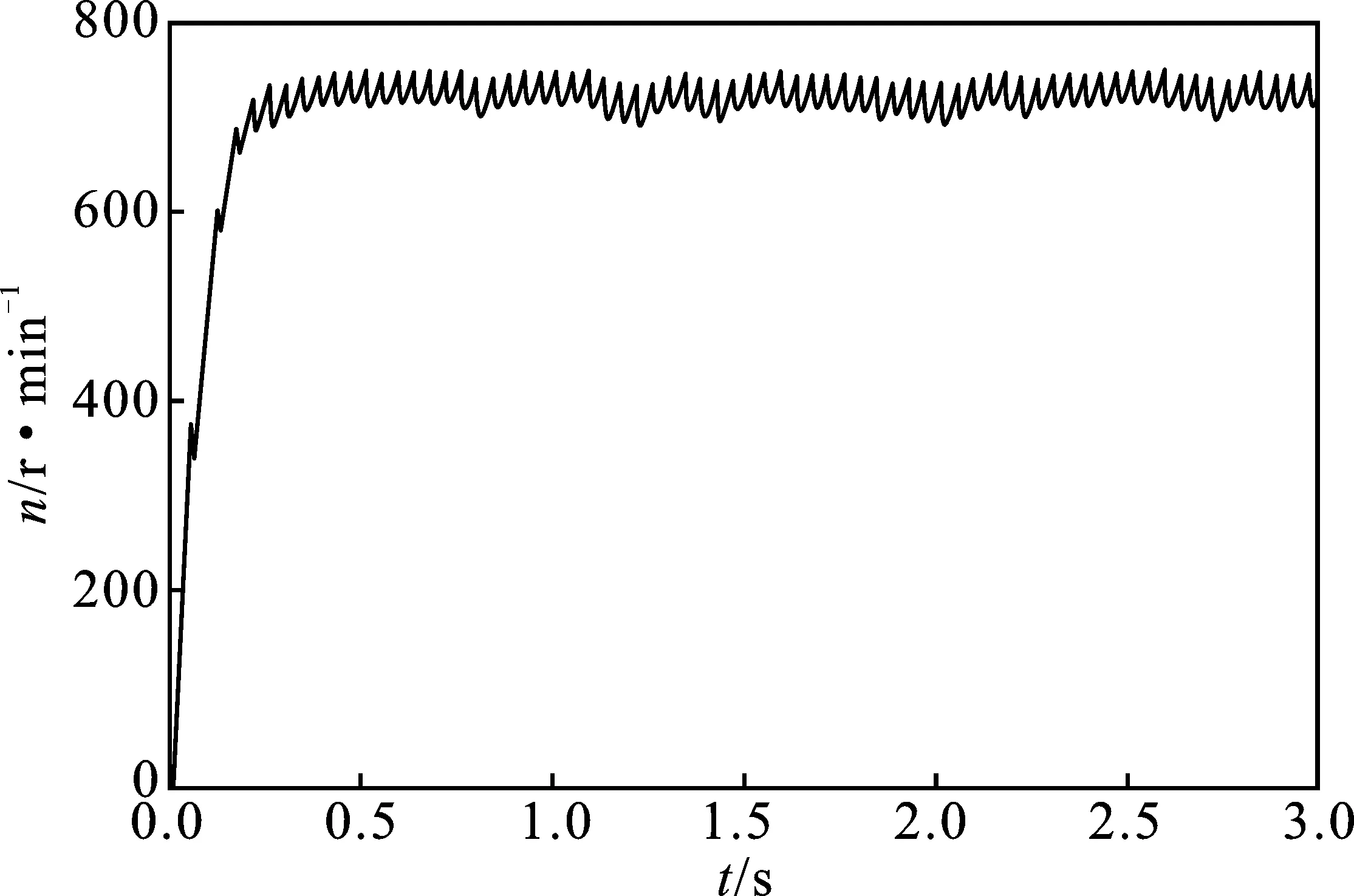
图13 带负载时转速响应Figure 13. Speed response under load

由图12可知，系统空载运行时，转速响应较快且较平稳。由图13可知，系统带负载起动时，转速响应较快但是平稳性差。这是因为电磁转矩波动较大引起转速波动，是单相无刷直流电机的一个缺点。带载稳态运行时反电势、电流、电磁转矩仿真波形分别如图14～图16所示。

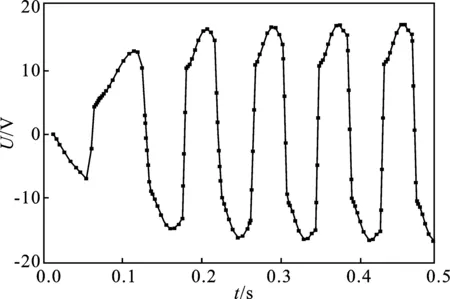
图14 带载时反电动势波形Figure 14. Waveform of counter emf under load

图15 带载时电流波形Figure 15. Current waveform under load

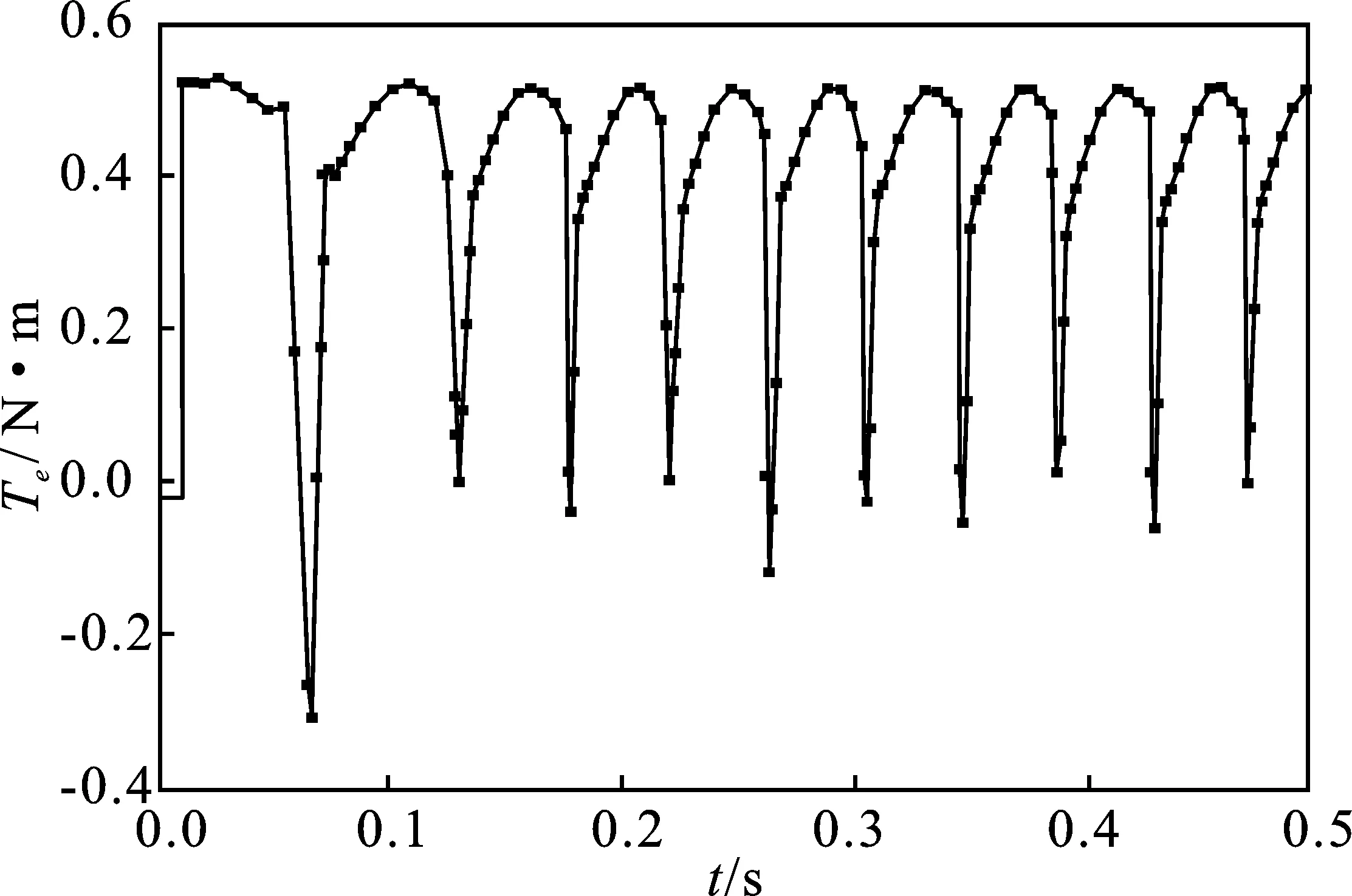
图16 带载时电磁转矩波形Figure 16. Electromagnetic torque waveform under load

由图14可以看出仿真反电势波形与有限元软件中的波形基本一致。图15中仿真电流曲线较准确的模拟了由换相造成的电流脉动。由图16可知电磁转矩可在短时间内进入稳定状态，但是存在较大的转矩脉动，与理论分析吻合。综上所述，仿真结果符合理论分析，验证了该仿真模型的正确性。

4 结束语

本文在介绍单相无刷直流电机拓扑结构特点的基础上，推导了单相无刷直流电机理想工况下的基本方程。本文根据工程实际需求，利用推导的功率方程并结合无刷直流电机的设计原则和设计经验设计出一台额定功率38 W，额定转速750 r·min-1的单相无刷直流电机。通过分析渐变气隙对电机起动性能的影响，确定了最优气隙长度。然后通过有限元软件Magnet搭建了二维有限元模型，仿真得到了电机的气隙磁密波形曲线和反电势波形曲线，仿真结果初步验证了设计方案的合理性。最后在Simulink环境中搭建了单相无刷直流电机开环控制系统的模型。仿真得到电机的转速、转矩变化曲线与理论分析比较吻合，证明了电机设计方案的合理性、电机模型的正确性和有效性。

本文总结的设计流程对该类型的电机设计具有一定的参考价值。在Simulink环境中搭建的电机模型为分析设计单相无刷直流电机提供了有效方便的方法。但本研究在设计中假设了一些理想情况，后期将对设计流程进一步补充完善并对电机进行优化设计，以使其更加符合实际应用需求。