基于系统空间结构约束的多线结构光条纹中心线提取方法

毛雪忆，李文国

(昆明理工大学 机电工程学院,云南 昆明 650500)

线结构光三维测量技术是一种非接触式测量方法，被广泛应用于智能制造[1]、医学诊断[2]、工业产品设计[3]等领域。光条图像中心点的提取是线结构光视觉测量中的一项关键的技术。由相机采集到的光条图像中，条纹中心线包含了被测物体的表面三维轮廓信息，是物体表面三维重构的基础[4]。条纹中心线提取的精度直接影响三维测量的精度。

目前，最常用的线结构光中心线提取方法有几何重心法、阈值法、灰度重心法和Steger法等。几何重心法[5]和阈值法[6]利用光条图像在其法线方向上的灰度分布呈高斯分布的曲线特征，通过先检测光条图像的边缘，再取其中间点作为该法线方向上的中心点，用上述方法遍历整个光条来获得光条中心线。这两种方法处理速度快，但精度较低，对噪声敏感。灰度重心法[7]将光条纹法线方向上指定宽度区域的灰度重心作为该横截面上的光条纹中心点。这种方法在处理有噪声干扰或者光带亮度不集中等问题时，提取精度会明显下降。基于Hessian矩阵的Steger法[8]是对光条横截面上的灰度分布利用泰勒级数展开式来求极值，该方法精度高，但容易受到环境光的干扰而影响精度，不适用于有环境光的条件。

本文实验的系统结构是相机垂直向下拍照，发散型多线激光器倾斜投射。倾斜投射的发散型多线激光器会造成每一根条纹中心线偏移。本文的研究方法分为标定和测量两个阶段：在标定阶段进行相机标定，计算结构约束的参数以及各个条纹的偏移系数；在测量阶段，利用偏移系数求出条纹中心线。由于在测量阶段往往有环境光的干扰，故现有的中心线提取方法会存在较大误差，无法准确提取出中心线。本文提出的方法受环境光的影响较小，可提高测量系统的抗干扰能力。

1 方法描述

如图1所示，多线结构光条纹中心线的获取主要由图像获取系统和多线结构光条纹中心线提取系统组成。多线结构光条纹中心线获取系统由4个模块组成。由于在无环境光时，Steger法提取的条纹中心线的精度非常高，因此在计算系统空间结构参数时可采用此种方法。提取中心线后，对点云数据进行处理和误差分析。

1.1 条纹中心线粗提取

在无环境光下，对系统进行相机标定[9-10]，得到相机的内部参数和外部参数。粗提取条纹中心线算法步骤如下：

图1 多线结构光条纹中心线获取系统的组成Figure 1. The composition of the multi-line structured light stripe centerline acquisition system

步骤1通过图像采集设备采集多线激光条纹的原始图像，设图片中最中间条纹的编号为mid，其它条纹的编号如图2所示。对图3(a)所示的原始图像进行预处理，降低图像噪声[11]，得到图3(b)；

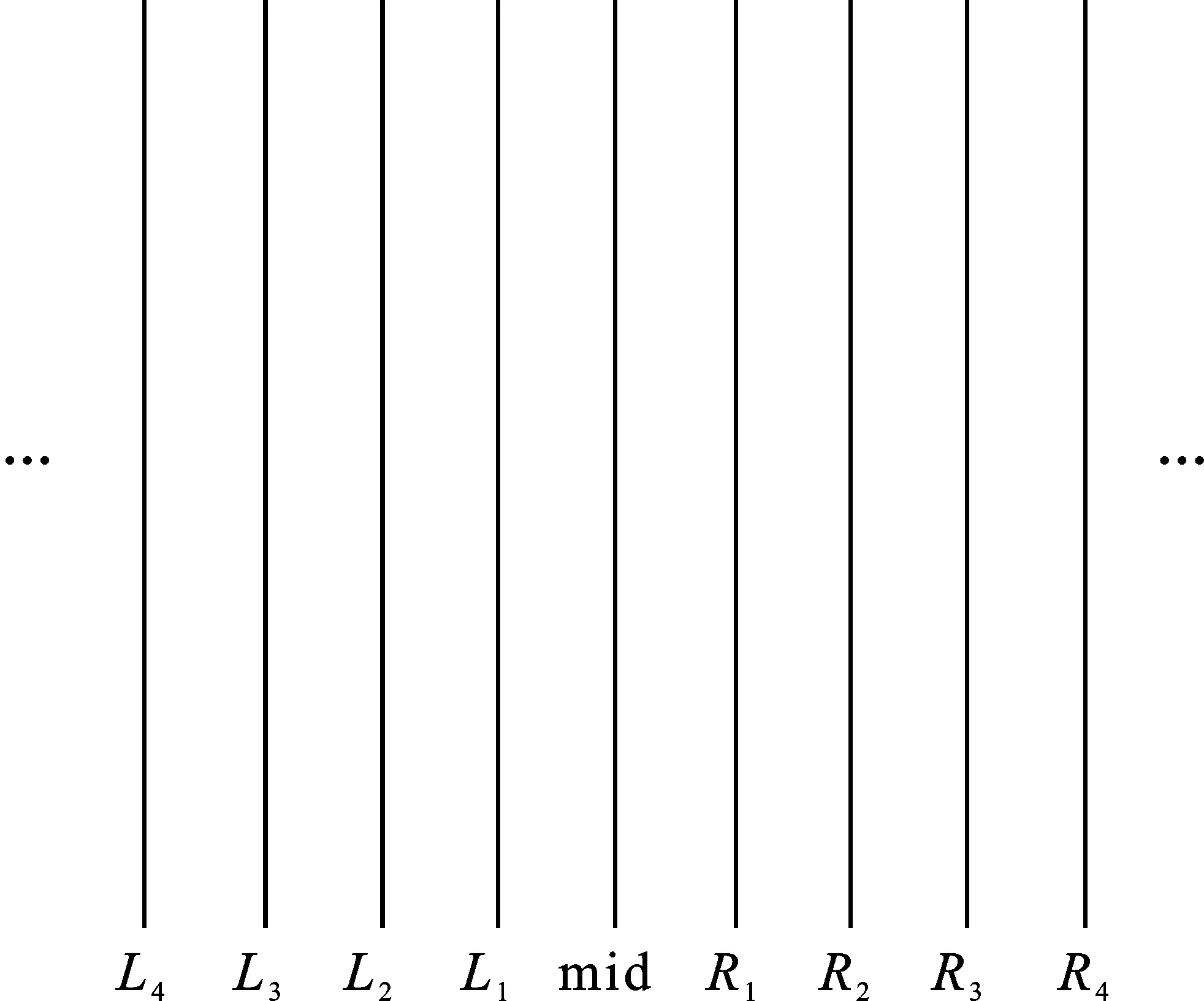
图2 条纹编号示意图Figure 2. Schematic diagram of stripe numbering

步骤2对图3(b)所示的原始图像进行边缘提取[12]并设置感兴趣区域(Region of Interest，ROI)，得到mid条纹边缘像素值和ROI图像，如图4所示；

(a) (b)

步骤3设置灰度值为R，遍历图4中ROI区域的点，当灰度值大于R时输出此点的像素坐标，灰度值小于R则舍去。具体的原理为：经过灰度化后的光条纹图像中有光条纹的部分的灰度值范围是240～255，无光条纹的部分灰度值范围是70～130，取灰度值R为200，即可输出图像中有光条纹部分的像素坐标；

步骤4条纹像素宽度d为

(1)

式中，d为mid条纹像素宽度；n表示每根条纹左、右两边缘像素对的编号；x2n和x2n-1表示条纹左右边缘像素对的横坐标；s表示每根条纹边缘左右像素对的总数；

图4 mid条纹ROI区域Figure 4. ROI area numbered mid stripe

步骤5取条纹像素宽度d的中间值t，与步骤2中的条纹左边缘的像素值相加，即为粗略条纹中心线的像素值p(u,v)。

1.2 系统空间结构参数计算

1.2.1 相机镜头中心坐标计算

本文的世界坐标参考系是以相机中心为原点进行计算的，故相机镜头中心坐标为(0, 0, 0)。

1.2.2 光斑中心的世界坐标的计算

提取图3(b)中的光斑边缘，ROI图像如图5所示，均值提取光斑像素坐标，求得光斑中心点的像素坐标，并转化为三维坐标(xc,yc,zc)。

图5 图像边缘提取Figure 5. Image edge extraction

1.2.3 激光器发射中心的世界坐标的计算

激光器发射中心的世界坐标的算法步骤如下：

步骤1采用Steger算法提取图中3(b)中L12和R12条纹中心线像素坐标[13]，利用相机内、外参数将中心线的二维像素坐标转换为世界坐标系下的三维坐标；

步骤2通过随机抽样一致性算法[14](Random Sample Consensus，RANSAC)求得L12和R12所在光平面方程[15]；

步骤3将L12和R12所在的两条光平面相交，得到空间点向式直线方程

(2)

式中，(x0,y0,z0)是激光器发射中心P的三维坐标值；a、b和c为直线的方向向量；

步骤4光斑中心点(xc,yc,zc)与激光器发射中心的世界坐标(x0,y0,z0)的连线的方程为式(3)。

(3)

由系统空间结构可知，式(2)与式(3)相交且垂直，垂足即为激光器发射中心点，如图6所示。联立两个方程，求得垂足(激光器发射中心)的世界坐标(x0,y0,z0)。

图6 光斑中心点与光平面相交线作垂线的空间关系图Figure 6. The spatial relationship diagram of the vertical line between the center point of the spot and the light plane

1.3 利用系统结构约束计算偏移系数

1.3.1 编号为mid条纹的偏移系数计算

空间结构约束模型如图7所示。由发散型多线激光器特性知[16]，在以激光器轴为参考时，mid条纹的强度分布为标准的正态分布，如图8所示。正态分布函数如式(4)所示。

图7 空间结构约束模型Figure 7. Spatial structure constraint model

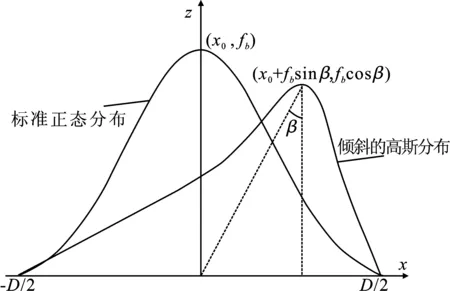
图8 倾斜的高斯分布函数图像Figure 8. Tilted Gaussian distribution function image

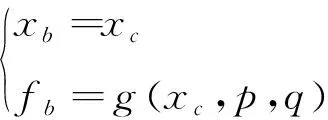
(4)

式中，xc为光斑的x坐标；p为正态分布对称轴的位置；q为的条纹宽度。

由章节2.2得到的参数坐标可以确定图7模型的位置。使用本模型前，可以通过结构调整使相机的世界坐标中的y值与激光器发射中心的y值相同。因此，可用x、z坐标求得夹角β(光斑中心点坐标到相机坐标的连线与光斑中心点坐标到激光器发射中心点坐标的连线的夹角)的三角函数关系为

(5)

式中，x0和z0为激光器发射中心点的坐标；xc和zc为光斑中心点的坐标。

mid条纹的光平面与法线交点A的坐标为

(6)

如图9所示，求得中心线偏移量e与偏移系数k0为

e=xA-x0=fbsinβ

(7)

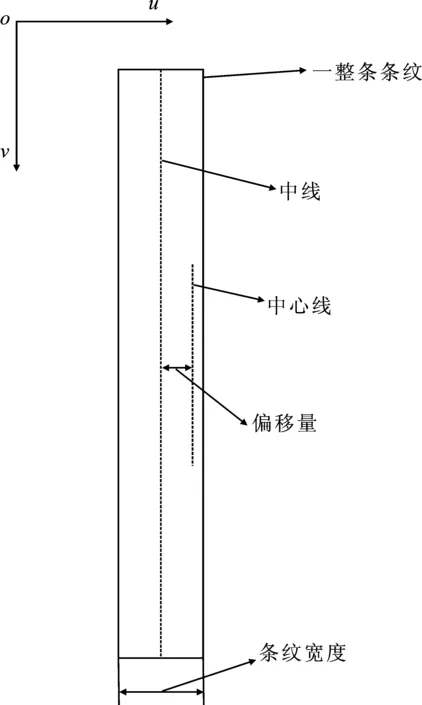
图9 像素坐标下的一整根条纹Figure 9. A whole stripe in pixel coordinates

(8)

式中，D为条纹的世界坐标宽度；e为粗提取条纹中心线x坐标与精确提取中心线x坐标之间的差值；k0为偏移量与条纹宽度的比值。

1.3.2 同一光条纹各个位置的条纹偏移系数特点

通过分析空间结构约束系统可知，同一线结构光投影到的不同空间位置上的点，其成像后的条纹偏移系数相同，具体分析如下文所述。

如图10所示，以光斑中心点为原点建立坐标系，设mid条纹光平面与其法线的交点A的纵坐标为h，则点A与原点O的直线方程为

y=cotβ·x

(9)

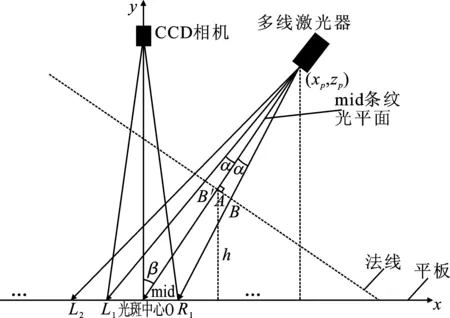
图10 以光斑中心为原点的系统空间结构图Figure 10. System space structure diagram based on spot center

将y=h代入上式，得点A的坐标 (htanβ,h)。

设在多线激光器坐标系下标准正态分布的高度为fb，如图8所示，可知在以光斑中心为原点的坐标系下

fb′=fb·cosβ

(10)

以光斑中心为原点的坐标系下，法点A上的高斯分布的最高点A′的y坐标为

y′=fb·cosβ+h

(11)

因为A′也在法点A与原点的直线上，故将y=y′代入式(9)，求得点A上的高斯分布的最高点A'的x坐标为

x′=fb·sinβ+htanβ

(12)

则A′的坐标为(y0·sinβ+h·tanβ,y0·cosβ+h)。

由式(9)～式(12)可得，此根条纹的中心线偏移系数k为

(13)

可知，偏移系数k与A点的纵坐标无关，即证明同一线结构光上各个点的条纹偏移系数相同。

1.3.3 所有条纹的偏移系数

如图13与表2所示，根据发散型激光器自身的特性，本文以25根条纹的激光器为例。根据制造厂家的生产制造规格数据，每两根条纹的夹角α为定值(1.11°)。由图7所示，求得与A点相邻的B点坐标如下

(14)

编号为r1条纹的中心线偏移量e1计算如下

e1=fb·cosβ·sinα

(15)

通过下式求得此根条纹的偏移系数

(16)

式中，D1为R1条纹的条纹宽度。以此类推，可求得其它所有条纹的偏移系数kn。

(17)

式中，n为条纹的编号数；Dn为条纹宽度。

1.4 最终的光条纹中心线的精确提取

由式(1)得到的条纹像素宽度d与式(17)的系数kn相乘得到条纹中心线的偏移量m偏。粗提取中心线像素坐标p初(u,v)与中心线偏移量m偏相加，即为条纹在物体上精确的中心线图像坐标l终(u,v)。

2 实验及测量数据对比分析

如图12所示，本实验所用到的设备有一部相机、一个镜头、一个激光器和一台笔记本电脑。其中激光器的参数由表1和表2所示。实验流程如图11所示。

图11 实验流程图Figure 11. Flow chart of experiment

图12 多线结构光实验平台Figure 12. Multi-line structured light experiment platform

表1 激光器的主要参数

表2 激光器衍射角

图13 多线结构光示意图Figure 13. Schematic diagram of multi-line structured light

2.1 标定阶段实验

搭建一个无环境光的实验台，多线激光器倾斜入射，相机垂直拍照[17]。采用张氏标定法对相机进行标定，得到相机的内外参数。

将L12和R12光条纹所在的光平面进行拟合，得到这两条光条纹所在光平面方程

(18)

将两个光平面相交，得到空间点向式直线方程

(19)

均值提取图5光斑中心点后，将其转化为世界坐标(-0.055,-0.01,492.12)。光斑中心与激光器发射中心的世界坐标(x0,y0,z0)的连线方程为

(20)

联立式(19)与式(20),求得激光器发射中的世界坐标。

由图7中参数的位置关系，求得夹角β为20.778 3°。由式(17)求得所有条纹的偏移系数。

2.2 测量阶段实验及分析

标定阶段结束后，本文从斜平面、圆柱体高度和曲面拟合分别做了中心线提取实验，并与Steger法进行比较,其中斜平面和圆柱体高度拟合属于平面拟合。本文中的3个实验需要保证参数位置关系相同。

2.2.1 斜平面拟合实验及分析

如图14所示，调整使平面板倾斜于水平桌面。图15为Steger算法提取结果。

图14 平面板拟合实验结构Figure 14. Experimental structure of plane plate fitting

(a) (b)

由图15可以看出，当没有环境光时，Steger算法能有效提取条纹中心线；但是当有环境光时，Steger算法无法有效提取条纹中心线。

计算利用本文方法提取的中心点到标定板面的距离，测量其误差，并与采用Steger算法获得的结果进行比较，结果如表3所示。

表3 本文方法与Steger方法的误差比较

由表3可以看出，当没有环境光时，本文的方法拟合平面在测量精度方面与Steger算法处在同一个像素级(都没有超过0.005 mm)；当有环境光时，Steger算法无法有效提取中心线，而本文提出的方法依然能有效提取中心线，且能将精度控制在0.007 mm以内，说明本文方法除了可以控制精度，还具有较强的抗干扰性。

2.2.2 圆柱体高度拟合实验和分析

本实验在无环境光下提取了圆柱体上表面的条纹中心线，对这些条纹中心线进行平面拟合。通过计算圆柱体上表面与平板之间的距离，得到了圆柱体的高度。本文使用的标准圆柱体的高为70 mm，实验如图16所示，误差分析如表4所示。

(a)

表4 圆柱体高度误差

由表4可以看出，在无环境光时，Steger法拟合圆柱高度的百分比平均相对误差为0.74%，本文的方法拟合的百分比平均相对误差为0.686%，比Steger法提取的精度提高了0.054%，可见在无环境光时，本文的方法能较准确地提取出条纹中心线。

2.2.3 半球体曲面拟合实验及分析

曲面拟合实验采用的是直径为50 mm的半球体，本实验在环境光下进行，实验如图17所示。由图17(b)可以看出，Steger算法提取的条纹中心线存在断口和缺失等问题，无法准确有效地采集到半球表面的点云。

(a) (b)

本文的方法是通过条纹宽度和偏移系数来计算条纹中心线的点云。通过对半球物体上的条纹进行边缘提取，得到条纹边缘的点云，如图18所示。然后，将这些点云拟合成椭圆。同一根条纹的边缘线有两条，拟合椭圆是一个同心椭圆。最后通过两个椭圆的短半轴相减，得到球体表面条纹像素宽度，从而获得条纹中心线点云。

图18 曲面条纹边缘提取Figure 18. Edge extraction of surface stripes

本文通过6组实验进行验证，其中一组计算出的点云图如图19(a)所示。对这些点云进行曲面拟合[18-19]后的结果如图19(b)所示。半径误差如表5所示。

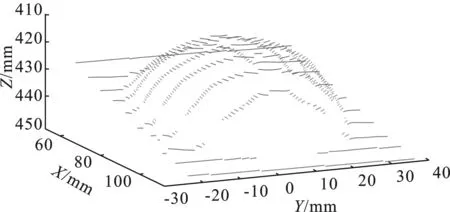
(a)

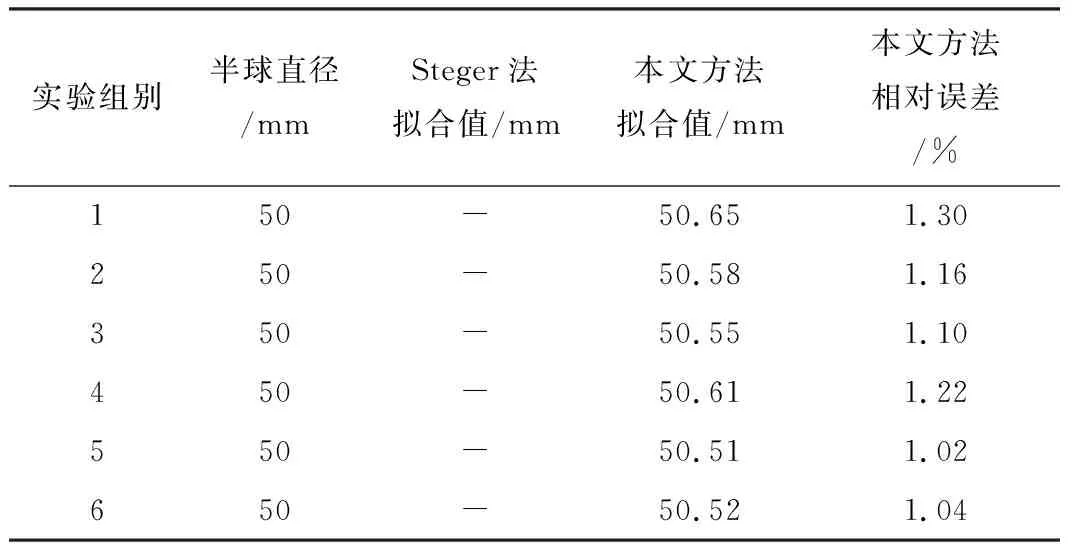
表5 有环境光时半球直径误差

由表5可以看出，在有环境光时，Steger算法无法进行半球点云拟合，而采用本文的方法提取条纹中心线，重构半球后误差为0.57 mm，百分比相对误差为1.14%，比高度拟合的平均相对误差增大了0.435%。该结果说明在曲线拟合时，精度会因为条纹的弯曲而增大，进而说明本文的中心线提取方法更适用于表面相对平滑的物体。

3 结束语

本文提出了一种基于多线结构光中心线提取方法。因所使用的激光器为发散型激光器，故每根条纹的中心线都有不同程度的偏移，造成中心线提取存在误差。相较于其它的算法，该方法通过结构约束来提取中心线，在标定阶段搭建实验系统进行标定和计算偏移系数，在测量阶段只需通过检测条纹像素宽度，结合偏移系数系数通过数学计算便可求出条纹中心线。实验结果表明，该方法能在有环境光时准确提取中心线，抗干扰性好、精度高。实验结果证明，在有环境光干扰的情况下其它方法无法提取中心线，但是本文所提方法能有效提取条纹中心线。本文的方法在提取表面为平面的条纹中心线时的精度很高，但提取曲面物体的条纹中心线时精度不高，还需要进一步探索与研究。此外，当测量物体的表面为复杂表面时，得到的激光条纹无明显规律，条纹宽度无法准确获取，从而无法精确提取条纹中心线。在今后的研究中，也将针对这一问题进行探讨和改进。