基于声矢量场处理的海洋内波预警监测技术
姜 煜,张 敏,白兴宇,华生辉
(杭州电子科技大学 电子信息学院,浙江 杭州 310018)
海洋内波是发生在密度稳定层化的海水内部的一种波动,在海洋内部其振幅范围一般为几米到几十米,波长为几百米至几千米,周期为几分钟至几十小时[1]。作为一种极其普遍的海洋自然现象,海洋内波对海洋军事活动和海洋资源利用开发具有较强的威胁性和破坏性,是目前国内外海洋领域的研究热点[2-4]。
目前国内外海洋内波检测方法主要有两种:一是采用锚系仪器阵列、走航拖曳仪器、中性浮子探测和声学仪器等,通过检测海水流变引起的物理变化来获取和检测内波信息[5-7];另一种是通过卫星遥感观测,通过获取内波在波峰后和波谷后处产生的辐聚和辐散现象来实现内波发现与跟踪[8-10]。然而,利用海水流变检测内波的技术存在诸多问题:锚系仪器阵列在细结构方面存在严重缺陷,其安装仪器有限,不可能获得足够长的物理垂向和水平空间序列,且锚系链容易受海流拖拽力影响发生摇晃,多普勒影响显著[11-13]。走航拖曳仪器测量的缺点在于成本高,随机性强,检测海域范围小,同样无法做到全自主实时检测。卫星遥感观测主要通过合成孔径雷达(Synthetic Aperture Radar,SAR)来进行内波检测,最大优点是能够进行大面积实时观测。但该方法仅能检测海水表层的特定内波,不能直接对隐藏于海底的内波进行连续的观测。此外,SAR观测的精度也受到海面状况的制约[14-16]。
本文提出了一种基于矢量场处理的海洋内波监测方法。该方法利用超低频矢量传感器对海洋背景噪声场拾取的三维信息进行水平方位估计,确定跟踪的目标信号源。本文从海洋内波水动力能流物理特性进行切入。内波的传播引起三维声速剖面的变化,基于目标的声强信息,声场的起伏导致声源垂直维掠射角发生突变,当跟踪的目标声源掠射角在时间限度内突变幅度超过正常范围,即可判断内波的到来。为了验证该方法的有效性,本文采用数值仿真分析跟踪声源信号在受内波影响条件下的垂直维掠射角的变化,并与常规噪声场条件下的角度变化进行对比。
1 基本原理
1.1 内波引起声场变化
在夏季,内波会导致大振幅波动,振幅可达百米。内波活动导致温跃层剧烈起伏,使海水的声速分布产生剧烈变化,对水下声场造成较大的影响。
图1是内波存在时声速剖面变化图,则声传播路径上的声速剖面为
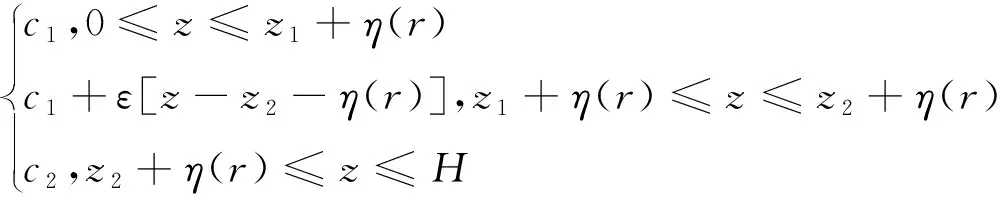
(1)
式中,η(r)代表内波随距离的位移;c1和c2分别表示温跃层上下声速;z1和z2分别表示温跃层上下边界深度;ε[z-z2-η(r)]为温跃层声速梯度。
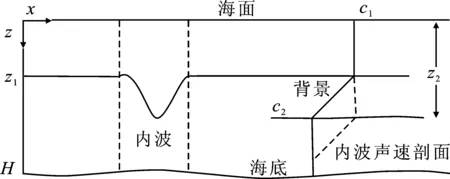
图1 内波声速剖面图Figure 1. Internal wave sound velocity profile
对于水平不变的浅海环境,远场声压可由简正波理论表示为
(2)
式中,ρ(zs)为深度zs处的介质密度;m为简正波号数;Ψm(z)为声源处简正波模态函数;Ψm(zs)为水听器处简正波模态函数;krm为简正波的本征值。水听器接收灵敏度取决于接收器处简正波模态函数Ψm(zs)的变化。内波引起的声速剖面的变化会导致Ψm(zs)改变,最终使信号声能流强度发生变化。
1.2 基于声矢量场处理的海洋内波监测
内波可引起声场起伏。由于声能流强度的改变,信号垂直维掠射角也随之变化。在海洋背景噪声场中搜索非协作声源目标,并通过监测目标信号的垂直维掠射角畸变来反演内波。
目前基于声压振速联合信息处理技术的声能流检测器主要为平均声强器与复声强器,其中复声强器为平均声强器在频域的实现形式。假设海洋信道中,声压与振速是同相位的,利用欧拉公式并经过傅里叶变换求解频域下质点振速分布
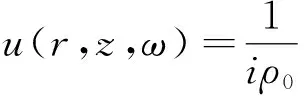
(3)
式中,∇p(r,z,ω)为声压梯度;r为水平位置;z为深度;ω为角频率;ρ0介质密度。通过声能流定义,得到复声强如式(4)所示。
I(r,z,ω)=p(r,z,ω)·u*(r,z,ω)
(4)
有限尺度声源所产生的辐射声场为相干信号,声压与振速是完全相关的。在海洋背景噪声中的各向同性噪声场为非相干信号,而非相干信号信息主要集中在虚部,即无功声强。经过互谱运算后相干信号会落在其实部,即有功声强
(5)
式中,Ii表示x、y、z各分量方向的有功声强。
利用有功声强在在x、y、z轴上的正交投影就可以估计出声源垂直维掠射角α,其表达式如式(6)所示。
(6)
对于多信号源方位估计,平均声强器只能得到合成声强流的方位。当存在不同频段范围的信号时,信号在频域上有明显的不同特征,此时使用复声强器法,能够分辨不同频率范围的信号目标方位,实现目标方位估计,得到目标垂直维掠射角。然后,对选定的目标信号进行跟踪并监测其垂直维掠射角,在内波到来时,即可得到跟踪目标的垂直维掠射角度变化情况。
图2为声矢量场时空频三维背景跟踪的内波识别示意图。如图2(a)所示,若不存在海洋内波,跟踪的某背景辐射源声信号将以A路线直达潜标,掠射角为α1。如图2(b)所示,当海洋内波来袭时,海水等温度面、介质密度层发生变化,引起声速剖面发生变化,导致海洋信道发生改变,声信号将以B路线到达潜标,掠射角为α2,与α1有明显的不同。潜标以此特征变化间接识别内波来袭,快速启动报警模块,完成报警职能。
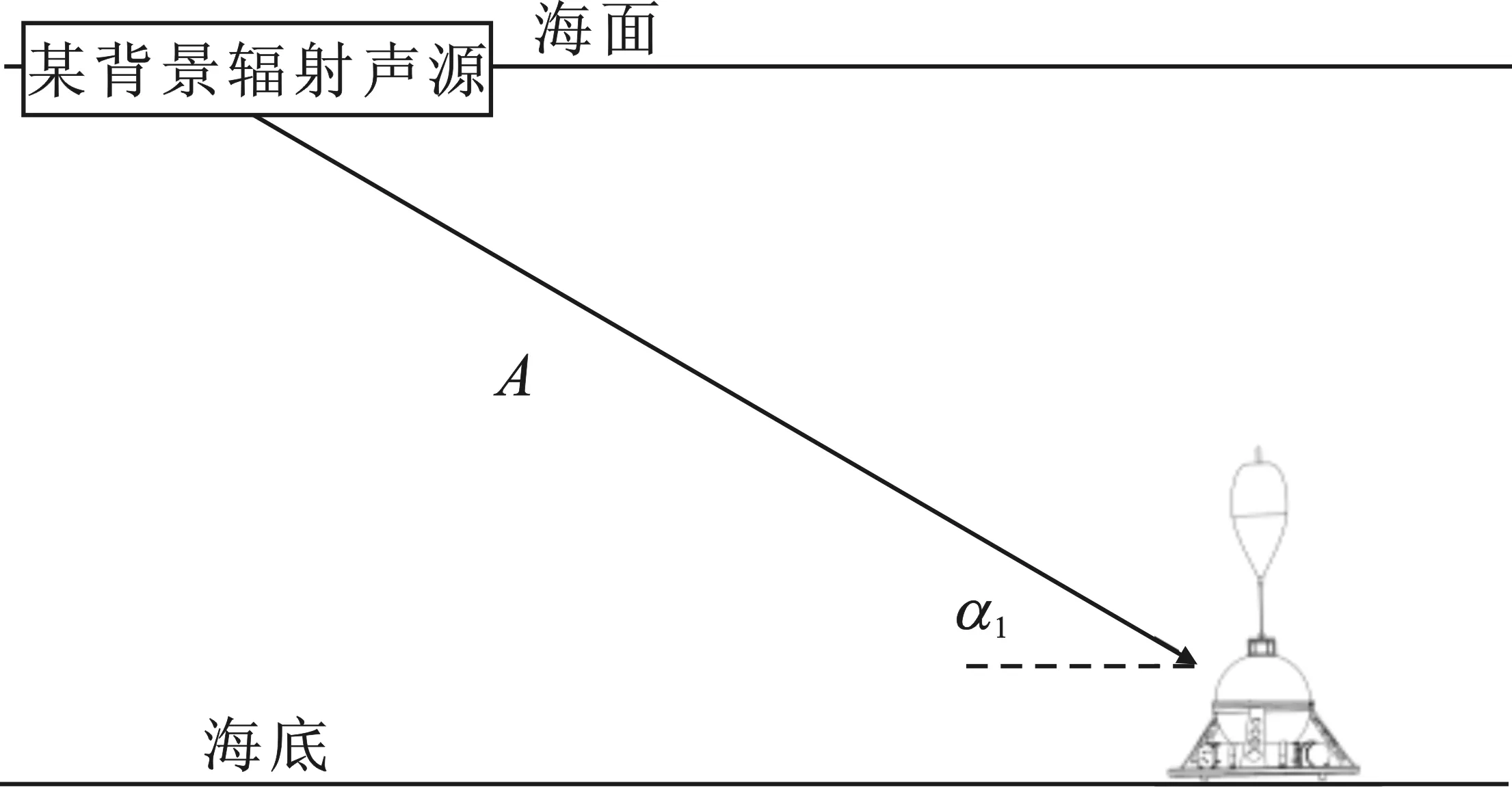
(a)
通过绘制时间(t)-频率(f)-方位(α)图,可直观地通过图上垂直方位角的跳变来判断内波的到来,该方法的算法流程框图如图3所示。
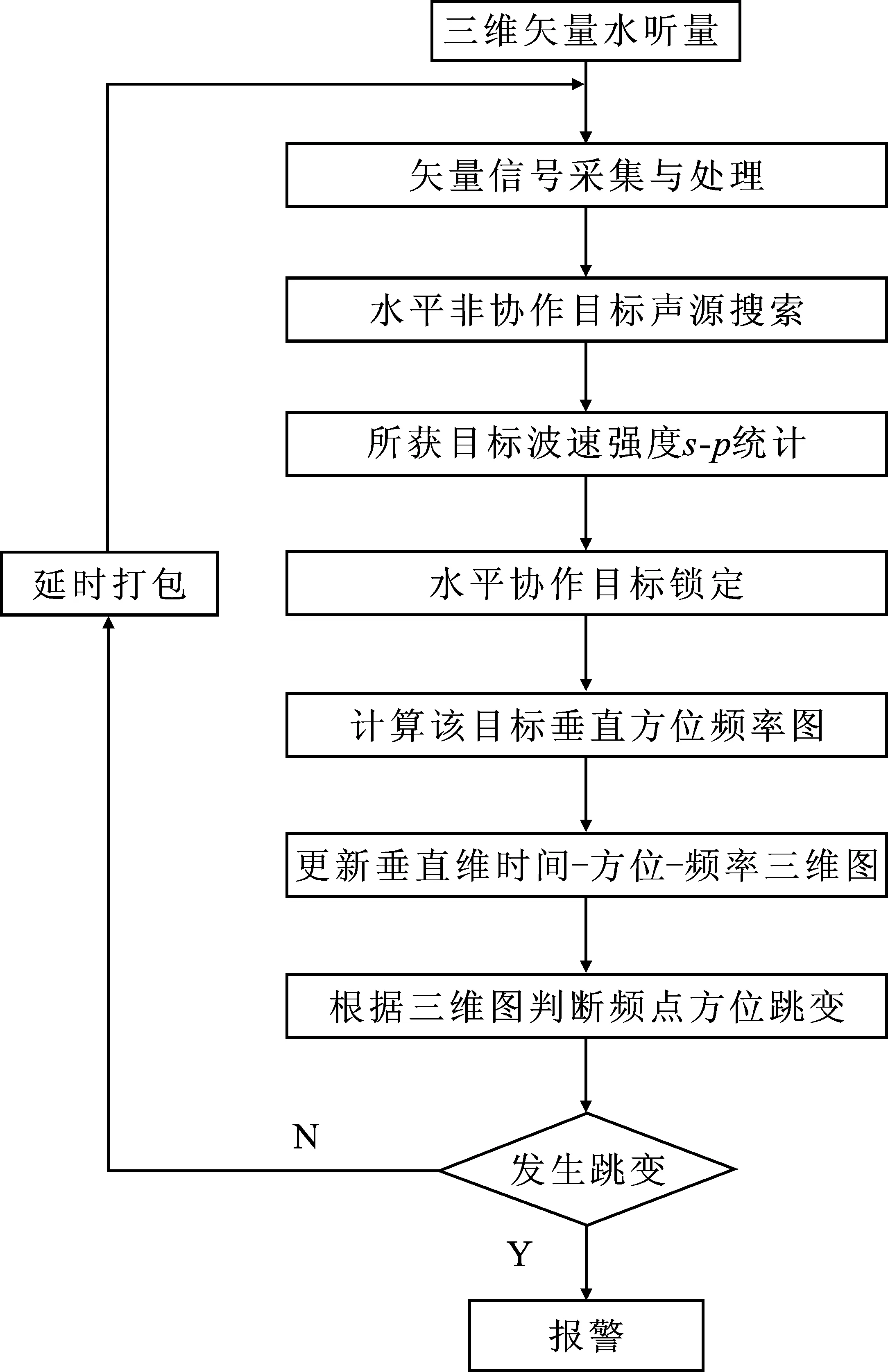
图3 矢量场内波监测原理图Figure 3.Schematic diagram of wave monitoring in vector field
2 方法实现
2.1 方位估计搜索非协作声源
矢量水听器接收到的水声信号为各方向声源的矢量和。当噪声源呈均匀分布时,接收到的声能流为零;当噪声源非均匀分布时,其环境噪声场呈各向异性。在实际的海洋环境中,噪声源的分布是不均匀的,海洋环境噪声场在水平方向呈现各向异性。同一接受点处的声压与互相正交的振速分量有着显著的相关性,通常均不为零,并存在显著的平均噪声声能流以及各个噪声源的合成声能流。
因受到干扰噪声源的影响,目标声源的定位会产生较大的误差。为提高方位估计精度,根据文献[17]提出的声能流矢量补偿方位估计算法和文献[18]噪声源定位方法,先粗略地获取目标所在空间扇区,确定主声源目标,将其他方位的噪声源均视为干扰噪声源;然后计算干扰噪声源的声能流,并从合成声能流中剔除干扰噪声源的声能流;最后再根据净声能流计算得到高精度的目标方位,锁定非协作目标声源。
如图4所示,确定目标水平方位角和垂直掠射角分别为(θ,α),Is为目标声能流,噪声源方位角和掠射角分别为(θi,αi),In为噪声源声能流,Is′与In′分别为Is、In在X、Y二维平面的正交投影。根据合成声能流原理可计算出各方位干扰噪声声能流在目标方位的分量为I′nx(θi,αi,f)、I′ny(θi,αi,f)、I′nz(θi,αi,f),获得目标声能流Is在各维度的分量为Isx、Isy、Isz。将目标方位声能流Is与In’进行矢量减,即为去噪的净声能流。

图4 矢量水听器三维声源声能流示意图Figure 4.Schematic diagram of three-dimensional sound energy flow of vector hydrophone
(7)
式中,N为在方位角为θi的频点个数;E[·]为求期望,即θi方位多个频点的平均声能流;K为不同方位的独立干扰噪声源个数。
根据净声强流I′sx(f)、I′sy(f)、I′sz(f)可求得较高精度的水平目标方位θ和目标掠射角α。
(8)
(9)
2.2 频点方位统计
根据式(8)计算出每一频点对应的水平方位θ,通过直方图统计法对各个频点所对应的方位角进行统计,统计强度最大值所对应的目标即为跟踪目标。
对于宽带信号,可以对方位进行直方图统计。但是当目标信号是线谱信号且存在宽带强干扰时,宽带强干扰会在频点方位统计时掩盖线谱信号的方位,此时直方图统计不能对线谱信号进行准确方位估计。考虑到线谱在频域中特征比较明显,本文利用加权直方图估计方法对普通直方图估计进行改进。进行频点方位统计时,将频点的声能流强弱作为权重进行加权累计。
记方位角统计间隔为Δθ度,则空间角度所允许的间隔总数为
(10)
由上式可得到水平方位角的区间范围为0~Δθ、Δθ~2Δθ、2Δθ~3Δθ、…、(N-1)Δθ~NΔθ。扫描整个频带,得到对应的方位角度。假定各个频点估计方位落入各个统计角度间隔的数量分别为m1、m2、m3、…、mN,则计算如下统计量S(θ)
(11)
其中,Ss(f)为式(12)。
(12)
为避免宽带噪声干扰,本文使用加权直方图统计目标方位,最终得到角度-强度统计量S(θ),其角度方位反映了真实目标方位值。
根据统计图选取最高峰值对应的角度θ。为了实现对目标信号的锁定,再次扫描整个频带,提取方位角为θ的信号频带Δf,则此宽带信号即为跟踪的目标。然后,再根据式(9)计算目标的垂直掠射角跟踪监测角度变化。在正常的海洋背景噪声场中,声速剖面分层稳定,矢量水听器接收到正常传播的声源信号,目标俯仰角起伏平稳;内波来袭时,跃层的深度起伏引起声速剖面发生明显变化,直接导致接收到的目标信号垂直维掠射角突变。本文基于此来判断内波的到来。
3 数值仿真
在实际工程中,利用三维同振式矢量水听器进行信号的采集和检测。共有4路信号输出,分别是p、Vx、Vy、Vz,其中p为声压,不具有指向性;Vx、Vy、Vz分别为x、y、z方向的振速,具有良好的灵敏度和偶极子指向性。在海洋背景噪声场中,噪声谱具有宽广的频率范围。测量结果表明,在低频范围内,频繁的船舶航行是全球海洋噪声的主要来源。在5~500 Hz频率范围内,自然噪声谱与船舶的辐射噪声谱吻合良好。因此,本文选择跟踪这一范围内的低频信号来监测内波。
海洋背景噪声随着频率的变化由十分复杂的功率谱密度成分所组成,包括各向同性和各向异性噪声。在进行信号处理的过程中,各向同性分布噪声由类高斯白噪声生成,通过高斯白噪声激励FIR线性滤波器得到。各向异性成分由添加的各向异性噪声源的方式进行叠加,共同构成海洋背景噪声模型。
为验证本文所提算法的性能,本文利用 MATLAB 进行仿真,在仿真中模拟了3个中心频率分别为55 Hz、150 Hz、300 Hz,带宽均为100 Hz的宽带连续谱信号作为目标声源信号,其水平方位分布为 50°、100°和150°,对应的垂直掠射角为40°、80°、100°。然后叠加海洋背景噪声,其中各向同性噪声分成与各向异性噪声分成在实际处理频段内的比例为1∶1,各噪声源相互独立。
由拟定生成的信号源和噪声,作为水听器拾取的输入信号进行处理。通过水平方位目标估计方法,先抑制海洋背景干扰噪声,再计算出海洋中各频点对应的水平方位角,方位频点图如图5所示。
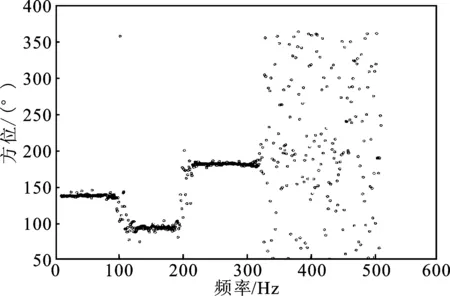
图5 水平维频点-方位图Figure 5. Horizontal frequency point-azimuth map
由图5可知,在拾取的信号带宽范围内,每个频点均对应着相应的方位角度。由方位的密集区域可直观的得到目标个数,但无法得到目标的信号强度,因此需要通过直方图统计法对各个频点计算得到的对应方位角进行统计。根据式(12)可得目标波束强度统计图,如图6所示。
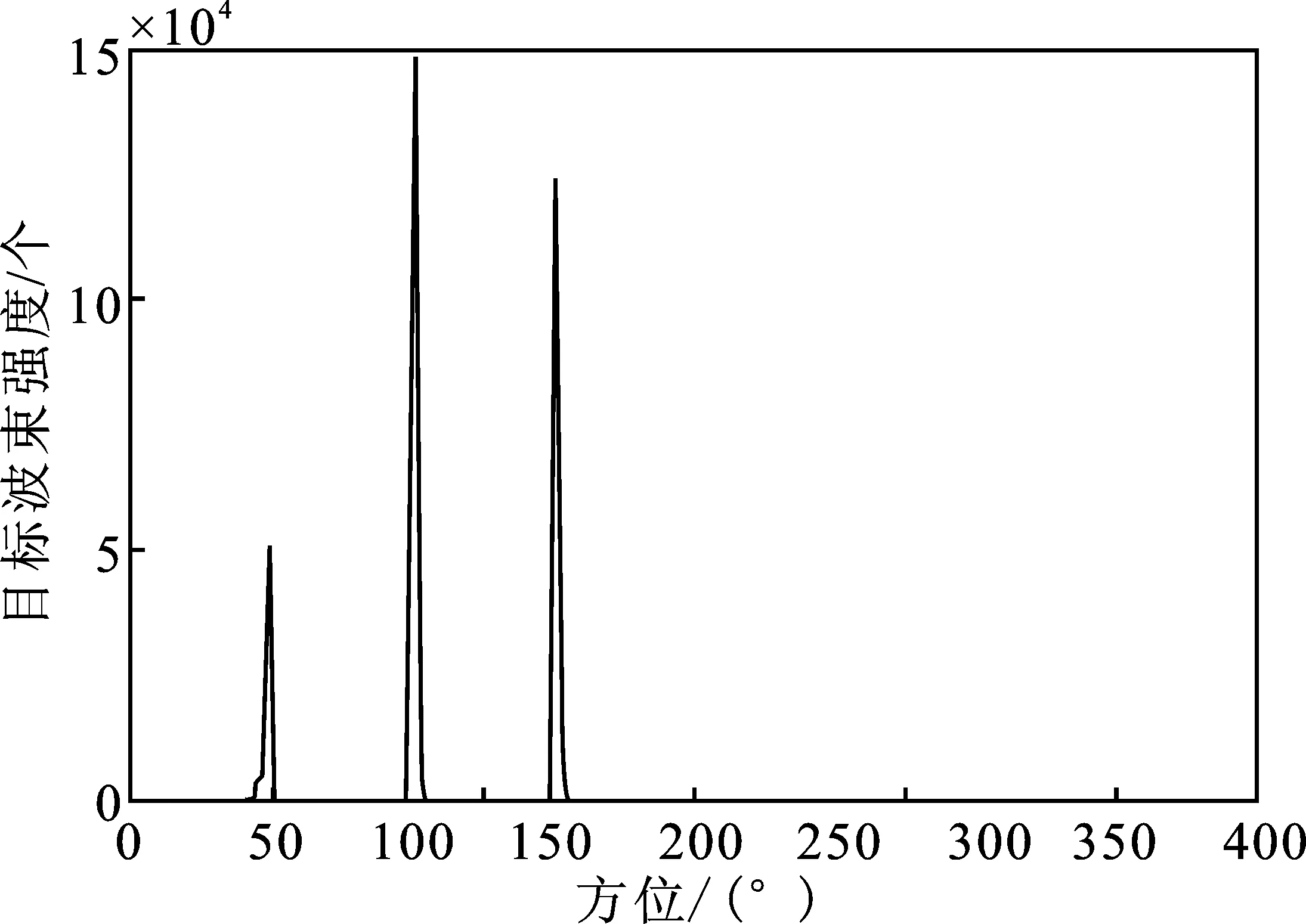
图6 目标波束强度统计图Figure 6. Statistics chart of target beam intensity
使用加权直方图估计方法来对频点方位进行统计,将频点的声能流强弱作为权重进行加权累计。由图6所示,存在宽带目标信号时,信号各频点所对应的方位角均在一定的区间范围内,而噪声频段各频点所对应的方位角呈随机分布,水平方位角为100°的目标信号波束强度最强,便选取此信号作为跟踪目标,跟踪监测其垂直维掠射角。
选定统计图中波束强度最强的信号作为跟踪目标,计算该目标频带范围内的垂直维掠射角,如图7所示。
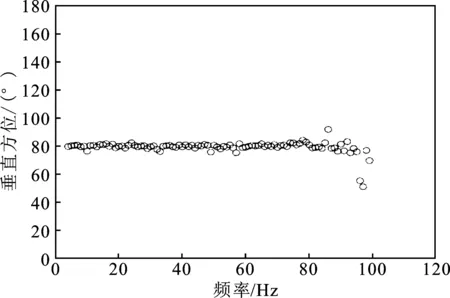
图7 所获目标垂直频率-方位图Figure 7. Obtained target vertical frequency-azimuth map
由图7可知,锁定的目标信号垂直维掠射角的方位为80°,与实验数据相吻合。在正常海洋背景环境中,同一目标信号源在其频带范围内所得垂直维掠射角基本保持不变,在误差范围内保持相对稳定。
在时限范围内,对垂直维频率-方位图进行更新,得到垂直维时间-频率-方位图,如图8所示。
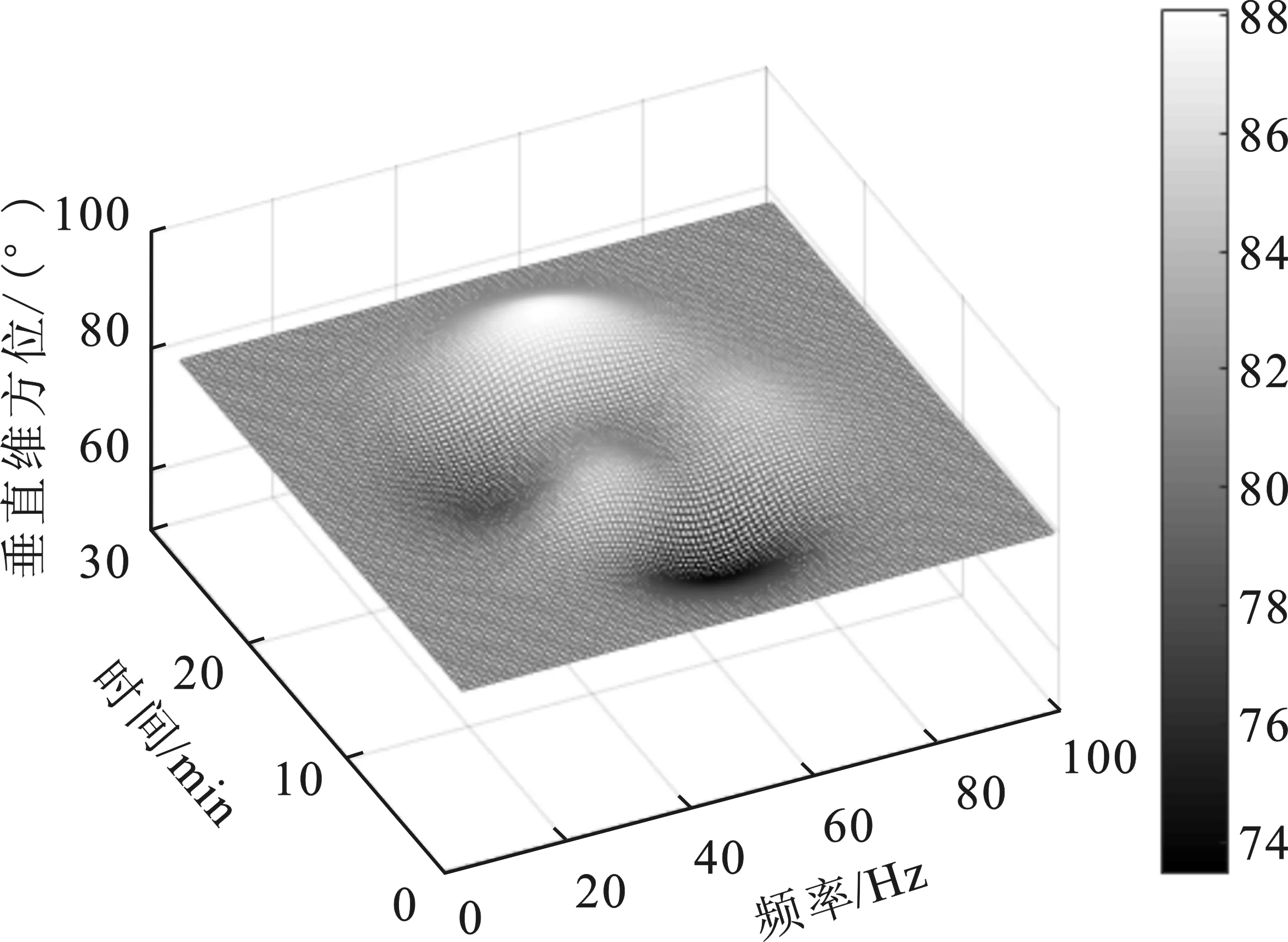
图8 垂直维时间-频率-方位图Figure 8. Vertical time-frequency-azimuth map
由图8可知,在无内波来袭时,跟踪目标在时限范围内,其垂直维方位掠射角呈略微起伏态势,在监测范围内的总体偏转幅度在5%以内,最大偏转幅度为10%。
海洋内波种类丰富多样,由于内波的多样性,从不同地点、不同时间、不同特征的内波得出统一的模拟结果较为困难。本文假设实际的海洋内波是由许多不同频率、不同波数、具有随机振幅和随机相位的正弦波线性叠加而成,以正弦函数来模拟内波介入,通过仿真得到了内波来袭时跟踪目标的垂直维时间-频率-方位图,如图9所示。
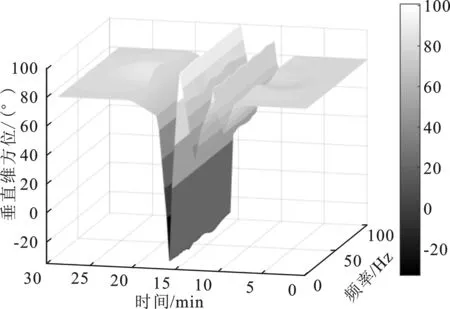
图9 内波来袭垂直维时间-频率-方位图Figure 9. Vertical time-frequency-azimuth map when internal waves strike
结合图8和图9可知,没有内波时,跟踪目标的垂直掠射角在其频带范围内略微起伏,起伏态势总体保持平稳;当内波来袭时,随着内波中心向水听器接收点的移动,由于内波引起海洋背景声速剖面的改变,声波向远离内波的方向偏转,产生一定会聚效应。根据劳埃德镜效应,固定接收点的能量呈现强弱交替出现,从图中可看出垂直掠射角也随之大范围的上下起伏。随着内波移动到接收点中心位置,水听器拾得目标信号声能流急剧改变,造成跟踪目标的垂直维掠射角产生最大的偏转角度,极大值从+80°的角度跳变到-20°,最大偏转幅度达到125%。当内波向远离声源的位置移动,偏转角度随之变小,随着内波超出影响范围,声源信号的传播不再受到影响,跟踪目标的掠射角恢复到正常角度,偏转幅度在5%以内。若在跟踪时限内判断为同一海洋内波,则结束跟踪,然后对海洋内波来袭数据进行加密打包处理,启动数据通信模块,完成报警职能,同时进行内波数据传输。
基于以上描述,依据海洋内波声学原理跟踪目标垂直维掠射角的变化,结合图像跳变特征即可判定内波的到来。与传统内波监测方法相比,该方法不需测量多种物理量变化,也打破了空间的束缚,可较为快速而精准地判断内波。
4 结束语
本文提出了一种基于矢量场处理的海洋内波监测方法,该方法利用超低频矢量传感器对海洋背景噪声场拾取的三维信息,先进行水平协作目标搜索来锁定跟踪的目标声源。由于内波的传播引起声场的起伏,因此通过监测目标的声强信息和垂直维掠射角的变化范围来判断内波到来。仿真分析结果证明跟踪目标声源垂直掠射角在正常海洋环境中变化范围在5%以内,浮动较小;当内波来袭,目标声源垂直掠射角发生突变,最大突变可达125%,突变至负向角度。海洋内波潜标监测技术通过背景跟踪、噪声抑制、角度监测并结合水下探潜技术可以实现现有仪器无法做到的海洋内波实时全自主识别。另一方面,潜标体积小,布放回收便捷,不需要大型吊放设备,可以使用渔船、小艇等进行布放和回收,成本较低,具有较好的实用价值。由于三维海洋背景的复杂性,本文主要通过简化后的内波模型代入算法演算仿真,未来的研究方向将基于真实的海洋内波传播模型来改进算法,通过处理实时的海洋环境数据实现内波监测工程化。

