复合材料火箭筒体的力学响应分析及建模方法研究
张 淼,隋 欣,党海燕,王宁飞
(1 北京理工大学宇航学院,北京 100081;2 北京特种机械研究所,北京 100143)
0 引言
复合材料具有良好的性能,使其在工程领域得到了广泛的应用。将复合材料应用于火箭筒体,可减轻质量,满足隐身、防弹等军事要求,提升火箭武器系统战术技术性能。近年来,随着复合材料在火箭筒体上的大量使用,如何更有效研究复合材料筒体的力学性能和变形特性对于火箭筒体设计优化有着重要的意义。在进行筒体研究时,其建模计算仿真是必不可少的步骤,建模方法的正确选择对于后续工作影响深远,因此筒体建模方法的研究十分必要。
文中基于有限元数值仿真的方法,以有限元计算软件ABAQUS为开发平台,分别采用实体-壳单元绑定与全部壳单元两种方法建立两种复合材料筒体的仿真模型,将仿真结果与试验数据进行了对比,结果表明,研究筒体强度时选择实体-壳单元绑定的方法建模获得的结果更贴合实际试验结果。
1 复合材料层合板理论及其非线性模型
1.1 理想层合板基本假设
根据力学相关理论,做以下假设:
1)层合板变形很小,且材料服从胡克定律;2)层与层之间理想粘接,无间隙,无粘接层厚度,无错动,且沿厚度方向变形连续;3)层合板中变形前垂直于中面的直线段,变形后仍保持直线且垂直于中面。
1.2 单层板任意方向上的应力应变方程
如图1所示,单层板任意方向上的应力应变关系满足:

(1)

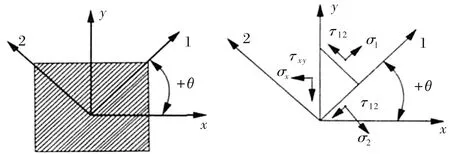
图1 单层板任意方向上的应力应变关系
1.3 经典层合板非线性本构方程
如图2所示,由各单层板应力沿厚度方向积分,可得到层合板单位宽度内力和内力矩方程为:

(2)
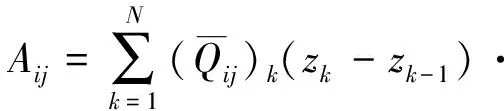

(3)

以上分析构成了复合材料经典层合板理论及其非线性数学模型。

图2 层合板内力、内力矩
2 有限元仿真模型
2.1 筒体模型及计算假设
模型为复合材料筒体,三维结构如图3。

图3 筒体模型
根据筒体模型,分别建立两种有限元仿真模型。筒的结构尺寸完全相同,筒体长度为5 000 mm,内径为1 000 mm,最大外径为1 100 mm,筒体包括内结构层、保温层和外结构层,内结构层为复合材料筒体,保温层为泡沫,外结构层为PE层和外蒙皮。
第一种建模方法:分别建立壳单元的内结构层、PE层和外蒙皮,实体单元的泡沫层。由于各部件之间是层层铺叠、紧密贴合的,故将内结构层与泡沫层、泡沫层与PE层、PE层与外蒙皮之间的相互作用都设置为绑定约束,建立的有限元仿真模型如图4(a)。其中,内结构层与泡沫层的绑定约束中内结构层为主表面,泡沫层为从表面;泡沫层与PE层的绑定约束中泡沫层为主表面,PE层为从表面;PE层与外蒙皮的绑定约束中PE层为主表面,外蒙皮为从表面。内结构层、PE层与外蒙皮的网格类型为S4R,泡沫层的网格类型为C3D10,网格数量为23 967。
第二种建模方法:直接建立壳单元筒体,内结构层、泡沫层、PE层与外蒙皮在同一部件上,在内结构层的基础上增加泡沫层、PE层与外蒙皮,建立的有限元仿真模型如图4(b)。网格类型为S4R,网格数量为2 970。
建模软件中实体单元和壳单元的薄厚显示存在差异,实体单元显示厚度而壳单元只显示壳体。

图4 有限元模型
为了便于计算,文中假设火箭为普通刚体。
2.2 材料参数
筒体结构材料主要是T300碳纤维、玻璃纤维、PE纤维和泡沫,各个材料体系的力学性能参数如表1~表2所示。
结构部分由材料以0°/90°两个角度为一周期交替缠绕,每个周期的材料厚度相同。

表1 泡沫的物性参数

表2 复合材料的力学参数
2.3 边界条件与载荷
工况1(发射工况):筒体内施加0.8 MPa的内压载荷,筒体前后法兰端面及鞍型架与筒体接触面位置设置固定约束。
工况2(起竖工况):筒段水平放置,在鞍型架位置通过工装施加集中压力载荷,大小为700 kN,载荷方向垂直于筒体轴向方向向上,筒体前后法兰端面及鞍型架与筒体接触面位置设置固定约束。
3 有限元结果分析
3.1 筒体变形分析
对于工况1,两种模型的筒体位移云图如图5。

图5 工况1两种模型筒体的位移云图

图6 工况1实体-壳单元模型中内结构层的位移云图
该工况下,实体-壳单元模型的最大变形位置在筒体下方中部,出现最大变形的部件为内结构层,云图如图6所示,壳单元模型的最大变形位置在前后法兰内侧。这种变形结果是由于筒体前后法兰都被完全固定,筒体中部位置离被固定位置最远,受力大从而变形最大,而内部加压筒体会产生变形,前后法兰内侧由于同时受到被固定位置的约束力和内部压强,导致此部分变形较大。
两种模型中最大变形出现的位置完全不同,这是因为:首先两种模型使用的单元不同,实体-壳单元模型中使用了两种单元,可以更真实模拟筒体内部单元之间以及各部件之间的力学响应,即实体单元泡沫层对壳单元内结构层的影响,而壳单元模型只使用了一种单元,且各部分建立在一个部件上,忽略了不同种类单元以及各部分之间的接触对力学响应的影响;其次各部分的材料属性不同,实体-壳单元模型中尽管用绑定约束各个部件,但受到较大压强时各部件的刚度差异较大,各个差异叠加后反映在仿真结果的差异更大,而壳单元模型中各部分建立在一个部件上,相对削弱了各部分之间的差异,因此利用两种模型计算后的仿真结果存在不同。
对比两种模型的变形云图,实体-壳单元模型的最大变形量为1.5 mm;壳单元模型的最大变形量为1.2 mm。
对于工况2,两种模型的筒体位移云图如图7。

图7 工况2两种模型筒体的位移云图
该工况下,鞍型架两侧变形量最大,这是因为鞍型架与筒体接触面固定,同时在鞍型架下侧施加载荷,导致鞍型架两侧变形最大。对比两种模型的位移云图,实体-壳单元模型的云图后侧变化梯度相对较小,变形相对均匀,最大变形出现在PE层,云图如图8所示,变形量为18.98 mm;壳单元模型的筒体整体变形较大,且云图后侧变化梯度相对较大,最大变形量为26.6 mm。

图8 工况2实体-壳单元模型中PE层的位移云图
3.2 应力分析
对于工况1,两种模型的筒体应力云图如图9。
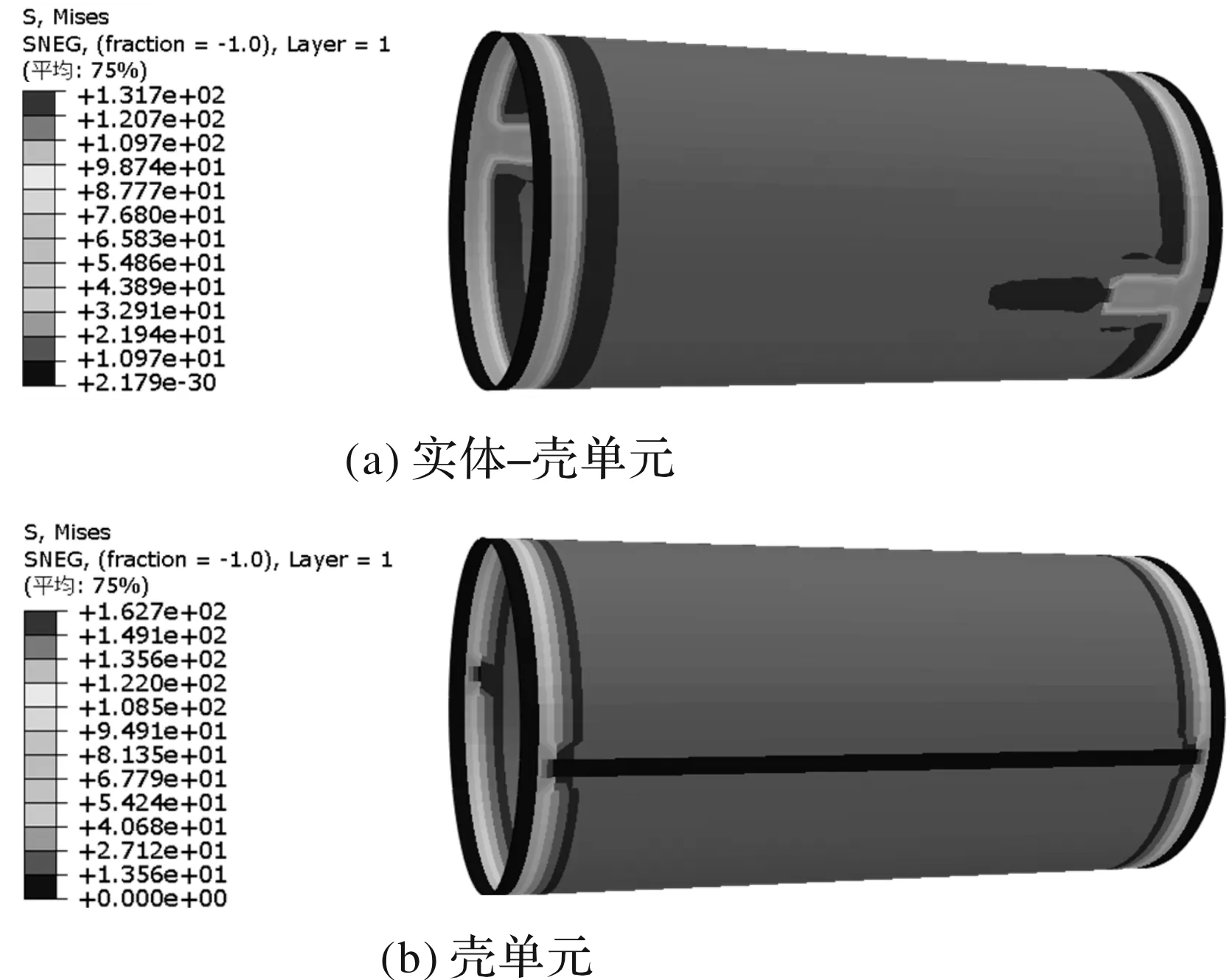
图9 工况1两种模型筒体Von Mises等效应力云图
该工况下,两种模型的应力最大位置均在后法兰前侧,这是由于此位置受力较大,但受力面积因变形减小,从而导致应力最大。实体-壳单元模型的最大应力出现在内结构层如图10,最大应力为162.7 MPa;壳单元模型的最大应力为131.7 MPa。

图10 工况1实体-壳单元模型内结构层的Von Mises等效应力云图
对于工况2,两种模型的筒体应力云图如图11。

图11 工况2两种模型筒体Von Mises等效应力云图
该工况下,两种模型的应力最大位置均在鞍型架两侧,这是由于鞍型架两侧受力最大,同时变形量大导致面积减小,从而应力变大。如图12,实体-壳单元模型的最大应力出现在PE层为349 MPa;壳单元模型的最大应力为169.7 MPa。

图12 工况2实体-壳单元模型PE层的Von Mises等效应力云图
3.3 应变分析
对于工况1,两种模型的筒体应变云图如图13。

图13 工况1两种模型筒体应变云图
该工况下,两种模型的应变最大位置均在后法兰前侧,这是由于此部分变形较大从而导致应变变大。实体-壳单元模型的最大应变出现在内结构层如图14,为0.129 9%;壳单元模型的应变云图更为均匀,最大应变为0.101 8%。

图14 工况1实体-壳单元模型内结构层的应变云图
对于工况2,两种模型的筒体应变云图如图15。
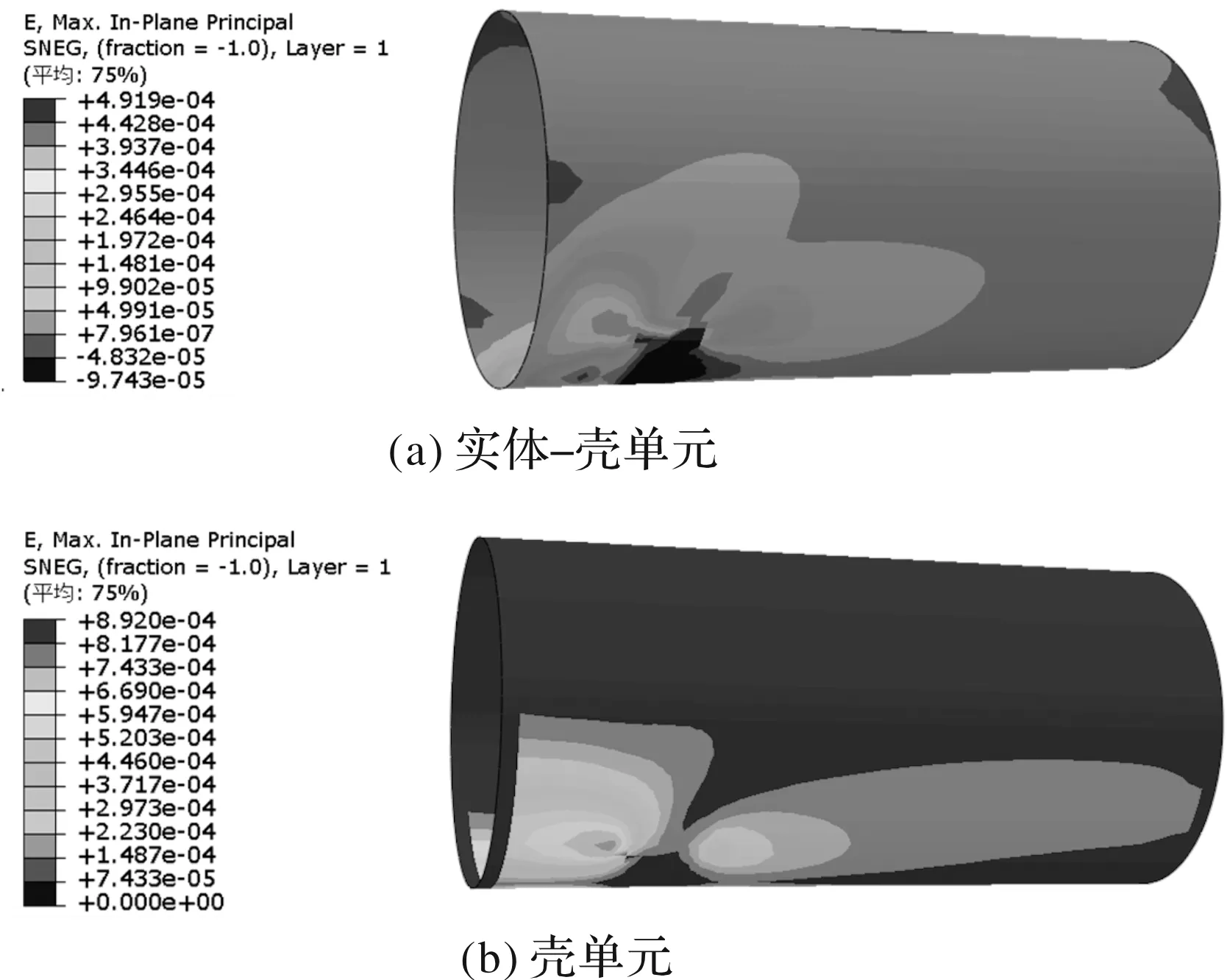
图15 工况2两种模型筒体应变云图
该工况下,实体-壳单元模型的最大应变位置在鞍型架右侧,为0.049 19%,最大应变出现在内结构层,云图如图16;壳单元模型的最大应变在鞍型架前侧,为0.089 2%。这是由于鞍型架周围的受力最大,变形最大,导致此部分应变最大。

图16 工况2实体-壳单元模型内结构层的应变云图
4 试验及结果分析
4.1 工况1结果分析
用内压试验来模拟筒段的发射工况。在筒体前部、中部、后部分别周向均匀布置3组应变传感器,每组8个如图17所示;在鞍型架位置及筒体中部均匀布置2组位移传感器,每组4个,后部布置2个位移传感器,共10个如图18所示。向筒段内部灌满水,并加水压,逐步加载至内压达到0.8 MPa,在内压为0.2 MPa,0.4 MPa,0.6 MPa,0.8 MPa时分别采集对应的应变及位移数据。筒段内压试验测试结果如表3。由试验结果可知,在水压达到0.8 MPa后,筒段的最大应变在后法兰前方右侧位置,为0.137 2%,最大位移在正下方中部位置,为1.57 mm。

图17 工况1试验应变测点示意图
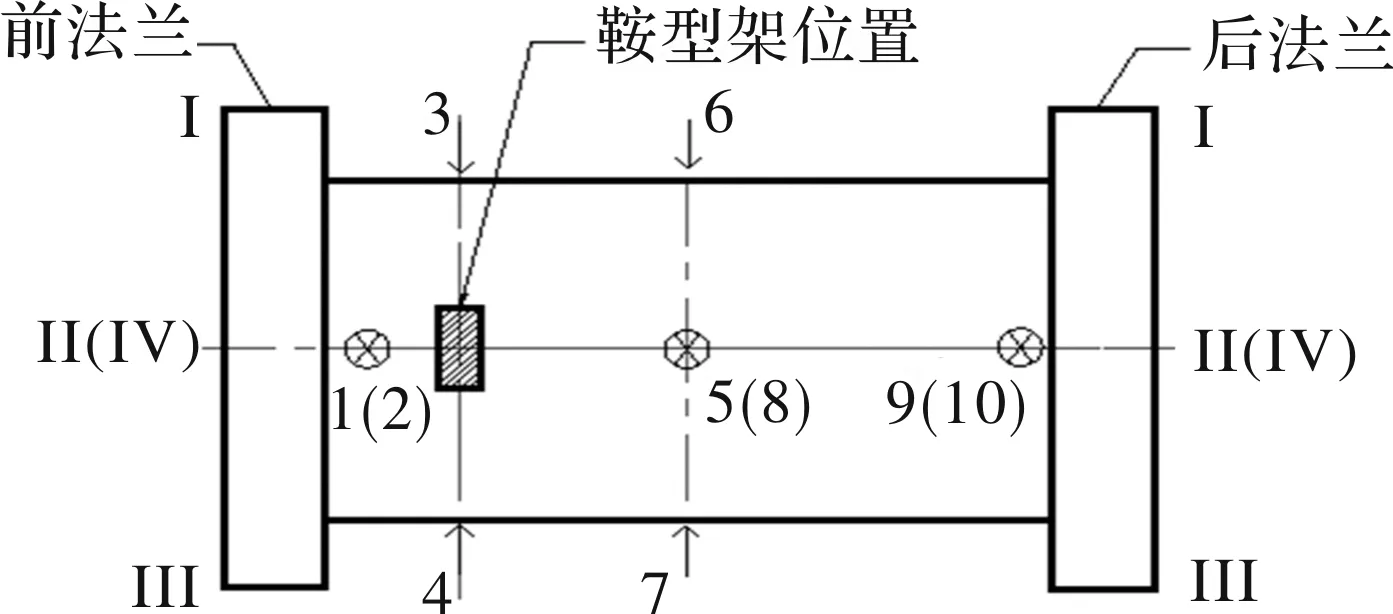
图18 工况1试验位移测点示意图

表3 内压试验应变测试结果 单位:με

表4 内压试验位移测试结果 单位:mm
4.2 工况2结果分析
用起竖试验来模拟筒段的起竖工况。在鞍型架位置周向均布20个应变传感器如图19所示;在筒体前侧和鞍型架位置布置2组位移传感器,每组3个,在筒体后侧及转接法兰位置布置2组位移传感器,每组4个如图20所示。
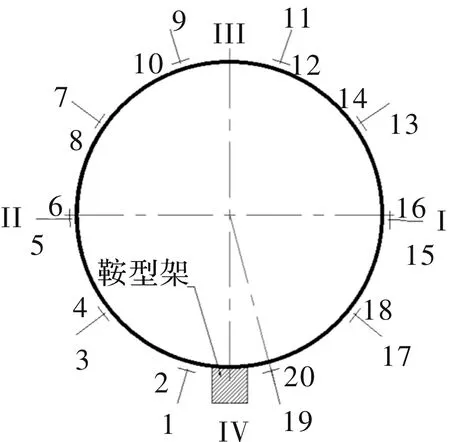
图19 工况2试验应变测点示意图

图20 工况2试验位移测点示意图
对筒段慢慢进行加载,当力传感器显示为70 t时停止试验,在载荷达到10 t,20 t,30 t,40 t,50 t,60 t,70 t时分别采集试验对应的应变及位移数据。筒段起竖试验测点数据结果如表5~表6。由结果可知,在加载到70 t后,筒段的最大应变在鞍型架右侧,为0.038 1%,最大位移在鞍型架前侧,为20.36 mm。

表5 起竖试验应变测试结果 单位:με

表6 起竖试验位移测试结果 单位:mm
试验测量结果与仿真计算结果对比见表7,可以看出,在误差允许范围内,实体-壳单元的建模方法与试验更为相符,且最大应变出现的位置也更吻合,所以实体-壳单元的建模方法更具准确性。

表7 试验测量结果与仿真结果对比
5 结论
基于有限元建模仿真软件ABAQUS,利用不同的建模方法建立了两种有限元模型,分别模拟了复合材料火箭筒体的发射工况和起竖工况,得到了筒体的应力应变和变形的数据,同时做了内压试验和起竖试验,得出以下结论:
1)发射工况下,筒体变形的最大位置在正下方中部,应力应变的最大位置均在后法兰前侧位置。
2)起竖工况下,筒体变形及应力应变的最大位置均在鞍型架附近。
3)在建立复合材料筒体的仿真模型时,选择实体-壳单元绑定的方法建模获得的仿真结果更贴合试验结果。
在今后的复合材料火箭筒体设计中,应对筒体中部及鞍型架部位适当加强,以提高筒体的力学性能;同时在仿真计算时应尽量选用实体-壳单元绑定的建模方法,以获得更真实的仿真结果。

