雷诺数对熔融态三硝基甲苯射流雾化的影响

左亚帅，张 帆，张会锁，王 蒙，王家祺，李 强，焦军虎

(1 中北大学机电工程学院，太原 030051；2 西北工业大学航海学院，西安 710072；3 山西中通高技术有限责任公司，山西 晋中 030600)

0 引言

废旧弹药回收处理技术概念的形成最早是在第二次世界大战前后。由于军事需要，世界各国，尤其是军事大国，都储备了大量弹药。这些弹药超过有效期限以后变得极其不稳定，引发了许多爆炸事件。因此，如何处理这些大批量的废旧弹药就成为了各国的重要课题。

传统的处理大批量废旧弹药的方法，如公海倾倒法、深土掩埋法等，不能从根源上完全消除炸药易燃易爆的不良特性，且销毁过程产生的大量废气和残渣会污染生态环境，因此被逐渐淘汰废弃。随着一系列环境保护文件陆续签署，世界各国都积极探究新的可持续的方法来处理废旧弹药，主要分为回收利用法和销毁法。回收利用法可将废弃炸药转化为民用炸药、烟花爆竹，甚至应用于医疗方面，可产生经济效益，但生产线价格昂贵，生产过程也存在大量不确定性，只能做小批量弹药的尝试。销毁法中的焚烧销毁法，虽然没有经济效益，但方法便宜，适合处理大批量的废旧炸药。文中对传统的焚烧销毁法加以改进，使其对环境友好。

目前的废旧炸药中，绝大多数的炸药为三硝基甲苯(TNT)，在燃烧过程中容易发生燃烧转爆轰(DDT)反应，如何控制其稳定燃烧在销毁过程中尤为重要。TNT熔点低，易转化为熔融态，可通过雾化工艺将熔融态的TNT形成均匀的、小颗粒的雾区并点燃，将不可控燃烧转化为可控的实验室燃烧。

郝俊修等设计了一套雾化销毁系统的样机，但在实验过程中缺少对材料的分析数据和雾化理论的支撑，试验具有偶然性，在使用过程中存在诸多安全风险。Dafsari等尽管在液体性质对喷雾的影响上进行了大量研究，但其研究重点为航空燃料，对TNT的处理没有参考价值。

基于三硝基甲苯的材料属性，研究雷诺数对于熔融态TNT的雾化影响，为后续的销毁研究提供理论支持。

1 物理模型及验证

雾化问题是一种十分复杂的三维流动，为了简化实际流动，也为了描述三维计算相对于二维计算无法比拟的简洁性和基础性，在研究中使用二维流场进行仿真计算。

1.1 数学及物理模型

TNT喷射问题的控制方程为不可压缩流和Navier-Stokes方程：

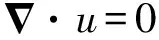
(1)

(2)

式中：,和分别表示速度、压力和时间。所有变量均使用喷嘴直径、材料密度和来流速度进行无量纲化处理，设为动力粘度，雷诺数的定义为：

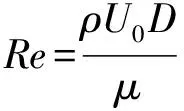
(3)

1.2 模型验证

由于国内外并未有对熔融态三硝基甲苯的雾化研究，参考Hattor等的雾化试验建立计算模型，以验证模型的准确性。试验所用喷嘴直径为0.3 mm，喷嘴长度为0.75 mm，雾化材料为柴油，环境压力3.0 MPa，喷嘴压力为32.0 MPa，基于实验模型建立简化的计算域如图1所示，喷嘴直径=0.3 mm，流向和展向分别为300和200，喷嘴中心位于展向的100处。

图1 二维计算域

文献[7]中的部分试验结果和文中与之相对应的计算结果如图2所示。可以看出，文中模型不仅可以很好的重现试验中的射流发展过程，也可以很好的表现燃料喷射过程中伞状头部的破碎和发展过程。

图2 实验结果与仿真结果对比图

1.3 网格验证

使用3种网格进行网格无关性验证，图2所示的结果所用的网格大约80 000个，另选用20 000和180 000两种网格进行对比分析，材料模型和边界设置与文献[7]一致。图3和图4分别展示了=90 μs时不同网格数下的索特平均直径和最远喷射距离，可以看出两个结果中，20 000的网格数据都严重偏大，而80 000网格数和180 000网格数的结果偏差较小，可以忽略。因此，考虑计算机性能和时间成本，文中选用80 000网格数进行后面的计算。

图3 t=90 μs不同网格数下的索特平均直径

图4 t=90 μs不同网格数下的最远喷射距离

1.4 材料模型

熔融态的三硝基甲苯近似为牛顿流体，采用PengRob材料模型参数，为防止温度过高TNT发生燃烧以至爆轰，以358.15 K至383.15 K温度下的TNT为例进行计算，关键材料参数温度、密度、运动粘度、表面张力如表1所示。

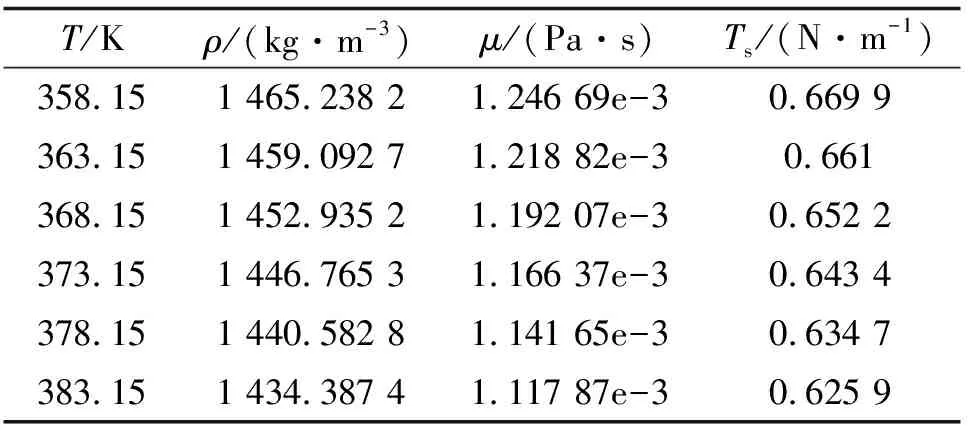
表1 材料参数表

在计算中选用了两个入口速度，分别为15 m/s和90 m/s；选用表1中的6个材料温度。经计算，对应的雷诺数别为3 526,3 591,3 656,3 721,3 785,3 849以及21 156,21 546,21 936,22 326,22 710,23 094。

2 结果与讨论

2.1 小雷诺数工况的结果

在低雷诺数3 526,3 591,3 656,3 721,3 785,3 849工况下，射流的喷射较为稳定，选取某一时间步的粒子速度分布如图5所示。射流进入空气后，高密度流体高速通过空气，在射流头部产生了瑞利-泰勒不稳定性，使得射流柱头部被挤压并向两侧推移，随着表面波的不断发展，射流柱头部在表面张力的作用下发生破碎并形成伞状头部。射流柱表面的液体随着射流柱的向前运动不断与空气发生剪切，并在其表面上发生开尔文-亥姆霍兹不稳定性，小液滴不断发生破碎和脱落。

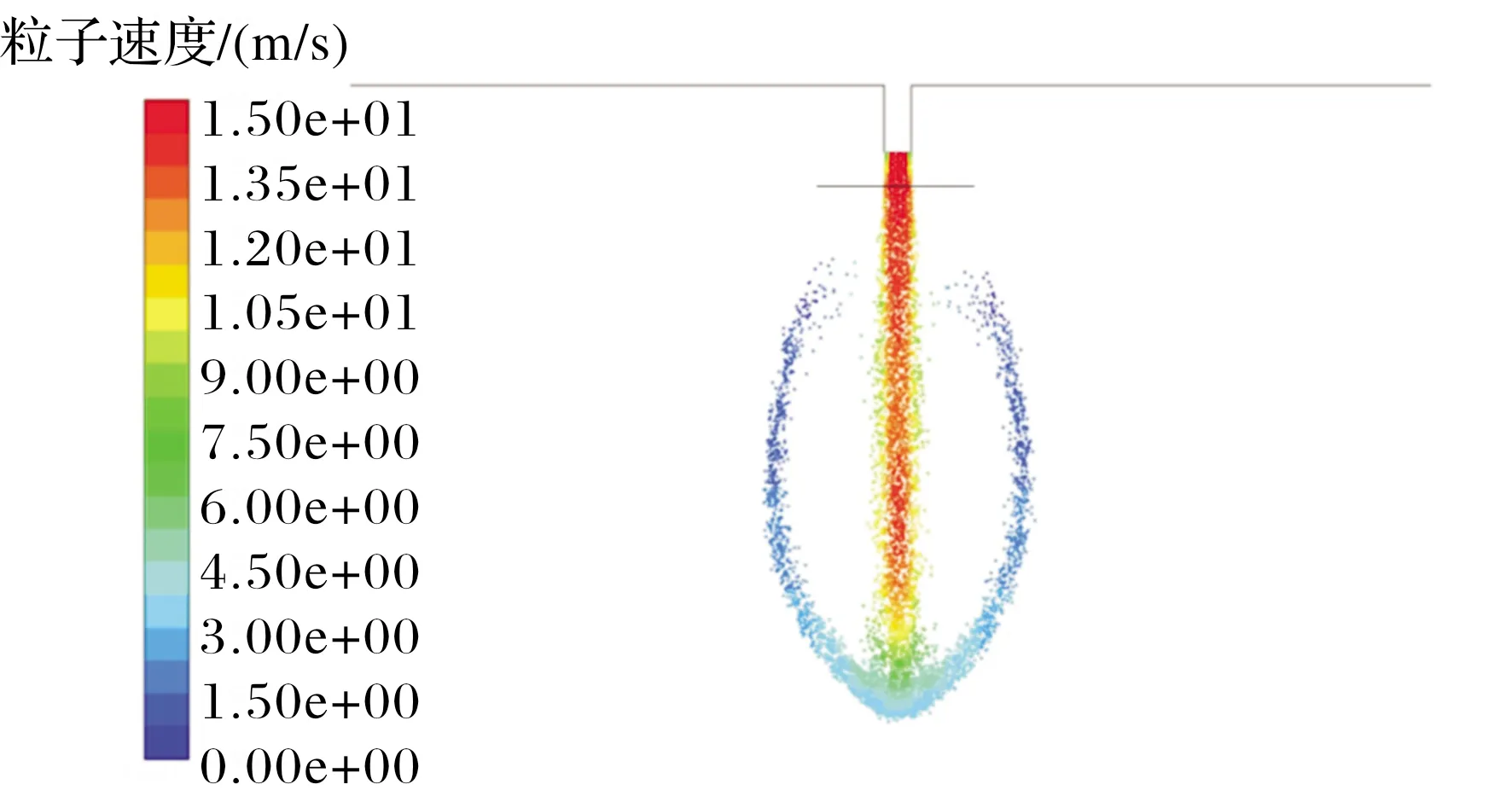
图5 Re=3656，t=10 ms粒子速度分布图

选择距离喷嘴=4的位置观测射流，即为图4内的黑线位置，展向上的平均速度如图6所示，横纵坐标均经过无量纲化处理。从图6(a)可看出，6组射流均在喷口轴线附近达到速度最高值，在轴线两侧速度迅速下降，速度的中心区域大约为6。然而各个雷诺数下的速度分布差异不明显，因此将速度最高点附近的区域放大处理为图6(b)。可以看出雷诺数为3 526，3 591，3 656，3 785这4个工况下，射流所能达到的最大速度随着雷诺数的增加而减小，雷诺数为3 721和3 849两组工况下的射流相较于其他组最大速度更大，但也是雷诺数大的最大速度较小。

图6 t=10 ms不同雷诺数射流的展向平均速度图

图7展示了平均速度衰减在轴线上的变化。从图7(a)可看出6组射流均在=11附近出现了一个波谷，然后速度升高，在=14附近达到局部最优再继续衰减至0，曲线的走势呈现出明显的一致性。为了观测6组数据的差异，把靠近喷口附近的区域放大处理为图7(b)，图7(b)与图6(b)呈现了很好的一致性，雷诺数为3 526，3 591，3 656，3 785这4个工况下，雷诺数越大，速度衰减的越快；雷诺数为3 721和3 849这两组工况较其他组工况的速度衰减较慢，但同样是雷诺数大的组，速度衰减较快些。

图7 t=10 ms不同雷诺数射流的轴线速度衰减图

2.2 大雷诺数工况的结果

在高雷诺数21 156,21 546,21 936,22 326,22 710,23 094工况下，射流表现为湍流剪切破碎模态，是湍流第一次雾化的典型模态，选取某一时间步的粒子速度分布图如图8所示。

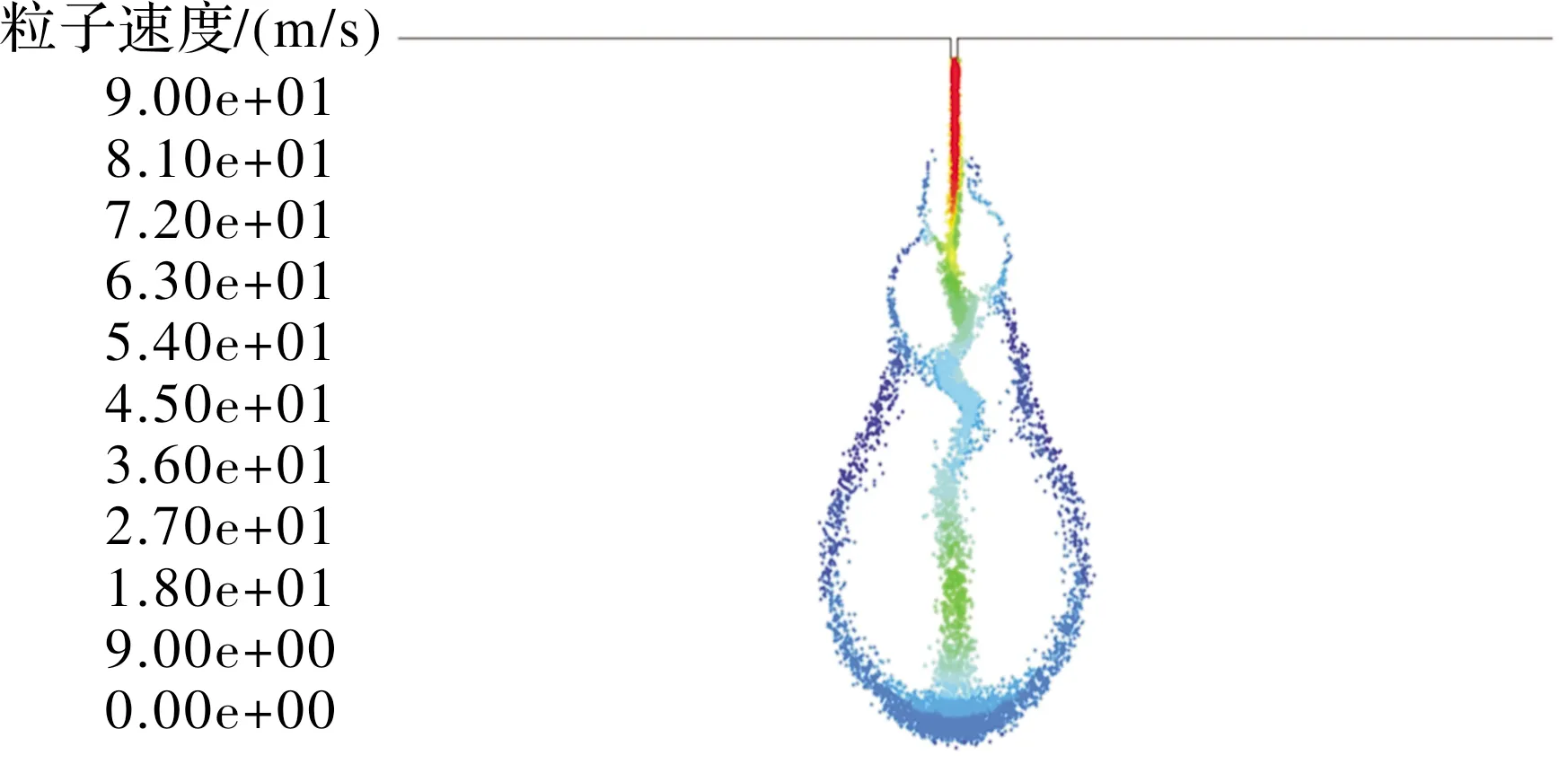
图8 Re=21936，t=10 ms粒子速度分布图

靠近喷口附近的小尺度涡引起了射流柱的小变形，然后小尺度涡溃散。受附近的涡和与空气的剪切力影响，射流柱的速度分布表现出一种明显的螺旋状。射流柱头部状态与低雷诺数相同，均在瑞利-泰勒不稳定性的影响下形成伞状头部，射流柱一边向前发展一边在开尔文-亥姆霍兹不稳定性的影响下破碎和脱落，脱落后的粒子与靠近喷口处的射流柱相互影响，加速了射流柱的雾化。

选择与低雷诺数工况相同的位置观测高雷诺数的展向位置速度分布，如图9所示，从图9(a)可以看出，与低雷诺数工况类似，6组射流均在喷口轴线附近达到速度最高值，在轴线两侧速度迅速下降，速度中心区域明显比低雷诺数工况小，只有约1。图9(b)为最高速度处的放大图，可以看出，高雷诺数工况下，平均速度分布呈“平顶帽”形状，但是这些速度的等速区长度不同，且等速区较长的组，速度分布也更对称。雷诺数为21 156，21 546，21 936，22 710工况下，最高速度随着雷诺数增大而减小；雷诺数为22 326和23 094两组工况单独呈现出随着雷诺数增大，最高速度减小的规律；且比前4组的最高速度都更大，等速区更长。

图9 t=10 ms不同雷诺数射流的展向平均速度图

图10显示了平均速度衰减在轴线上的变化，可以看出较图6而言，高雷诺数工况的速度衰减更混乱，更具备湍流的性质。射流在近喷口处不断振荡，从=65处开始完全衰减至0。将图10(a)分为两部分：图10(b)中包含雷诺数为21 156,21 546,21 936,22 710四组工况，其在衰减过程上保持了极强的一致性；图10(c)包含雷诺数为22 326和23 094两组工况，这两组工况在衰减过程上保持了一致性。

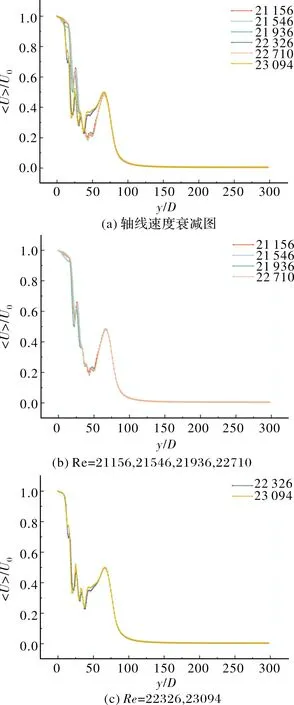
图10 t=10 ms不同雷诺数射流的轴线速度衰减图

2.3 两组结果对比

图11是两组速度工况15 m/s和90 m/s下的索特平均直径的对比图。当速度较大时，材料可以细化为更小的颗粒，且两组的曲线图趋势大致相同。然而，当材料温度为373.15 K时，平均直径体现了与其他5组极其不一致的情况，速度较小组反而颗粒略小，且该温度下的平均直径为全体最大。

根据以上分析，在雷诺数较小的工况下，射流集中在喷嘴口附近区域，射流柱的高速区较宽，射流速度沿轴向衰减快，射流边界层较厚，边界层动量低，导致射流与周围环境流体的相互作用减弱，射流柱处于较稳定状态，雾化主要发生在射流柱头部附近。随着雷诺数增加，射流呈现典型的湍流破碎模态，射流边界层与环境流体的剪切力增强，剪切层的非稳定性明显，液滴在剪切力的作用下从液柱上脱落并破碎成更小液滴，雾化在射流柱头部及射流柱均发生。

图11 两组速度下索特平均直径对比图

3 结论

对熔融态的三硝基甲苯喷射过程进行仿真模拟计算，探究雷诺数内的不同参数对于喷射的影响，得出以下结论：

1)雷诺数较低时射流状态稳定，射流速度沿轴向衰减快，速度在约=14处衰减至0；射流在=4展向上射流高速的核心区域大约为6。

2)雷诺数较高时射流呈现湍流的典型破碎模态，具有极强的不稳定性，射流速度沿轴向衰减较慢，速度在约=65处衰减至0；射流的展向速度分布呈“平顶帽”状，在=4展向上射流高速的核心区域大约只有1。

3)材料的温度对于雾化影响较小，但明显分为两组，一组是358.15 K,363.15 K,368.15 K,378.15 K；另外一组是373.15 K和383.15 K。两组具有相同的规律但各自独立。后面的研究将继续探究这一现象的形成原因。