基于多目标蝙蝠算法的加农炮内弹道性能优化研究
何新佳,马中亮,代淑兰
(中北大学环境与安全工程学院,太原 030051)
0 引言
火炮设计需要以内弹道计算为基础,在火炮内弹道计算中,火药装填条件以及膛内构造诸元的改变都会使内弹道的计算结果大不相同。火炮武器系统的内弹道设计是整个系统设计的核心,其先进性是衡量火炮武器系统先进性的主要指标,因此内弹道优化设计成了火炮武器系统优化设计的关键。对于加农炮来说,身管长,射程远,弹道低伸,因此追求其最大速度往往作为设计者考虑的首要目标,然而,当弹丸离开炮口后,膛内火药气体仍然具有较高的压力,并以很高的速度向外喷出,导致炮口压力较高,为了尽量降低这种有害的影响,必须对其炮口压力进行限制。在衡量火炮内弹道性能的指标中,弹道效率往往作为一个重要指标来考虑。因此在火炮内弹道性能多目标优化过程中,实现多个目标的均衡就成为一个重要的问题。
近年来,出现了很多典型的多目标优化算法,如NSGA-II、NSGA-III及MOEA/D等,这些算法采用的基本思想主要包括基于Pareto占优关系的MOEA算法和基于分解机制的MOEA算法等,其中,基于Pareto占优机制的原理对于处理低维多目标问题效果较好,可以得到分布更加均匀的Pareto最优解。
蝙蝠算法是受蝙蝠回声定位的特性启发而提出的新算法,相比于遗传算法和粒子群算法等,蝙蝠算法参数设置较少,收敛速度更快和求解精度更高,具有很大的应用潜能,因此文中结合Pareto占优机制,采用多目标蝙蝠算法对加农炮内弹道性能进行多目标优化,所得结果可为设计者根据实际需求提供相应的优化方案,并提高内弹道性能及发射安全性。
1 内弹道模型
1.1 加农炮经典内弹道模型
内弹道数学模型是弹丸在膛内运动过程的简化数学描述。对于100 mm加农炮,建立的基于管状发射药的内弹道模型如下:
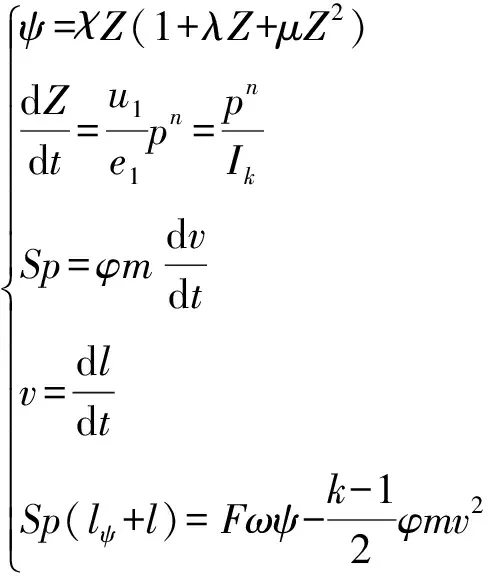
(1)
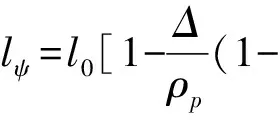
1.2 实验结果验证
文中所研究的加农炮原始数据可以参考文献[1]。利用原始数据,采用四阶龙格-库塔法对加农炮内弹道方程组进行数值求解,得到的膛压和弹丸速度曲线如图1所示。由图1知,曲线符合一般内弹道曲线的特征,很好地再现了火炮膛内的压力变化及弹丸的运动规律。
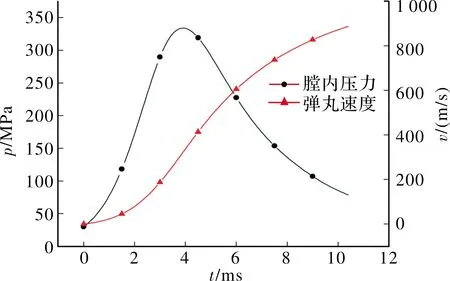
图1 膛压和弹丸速度曲线
取特殊点值与火炮射击实验数据进行比较,如表1所示。由表1可得,计算数据与实验值吻合较好,说明采用的加农炮内弹道数学模型可以准确描述弹丸在火炮膛内的运动规律,因此可以用来对加农炮的内弹道性能进行多目标优化研究。
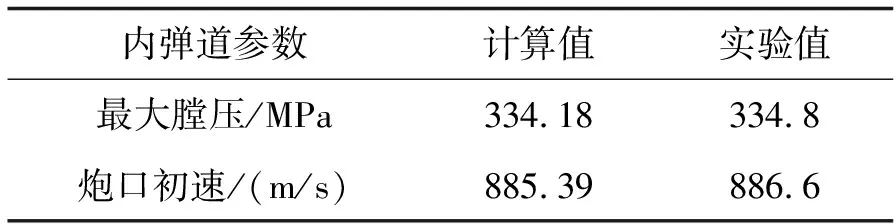
表1 计算值与实验值的比较
2 多目标蝙蝠算法
2.1 蝙蝠算法
蝙蝠算法主要模拟了蝙蝠通过回声定位系统来寻找食物的行为。每一个蝙蝠有4个属性,当前位置、当前速度、回声频率以及回声响度。蝙蝠算法中每只蝙蝠有2种行为:1)更新频率,更新位置;2)随机飞行。蝙蝠算法的假设如下:
1)全部蝙蝠都使用回声定位来感知距离,并且都可以判断出是食物还是障碍物。
2)响度从一个正值变化到最小值。
3)频率在[,]范围内,对应的波长在[,]范围内。
4)蝙蝠在一定位置以一定速度随机飞行,且可以自动调整发射脉冲频率或波长,并根据相对距离调整脉冲发射频率。
对于第一种行为,每只蝙蝠在速度更新之前会先随机更新其超声波频率:
+1=(,)
(2)
式中:和分别为频率的最小值和最大值;为0到1之间均匀分布的随机数;为当前迭代次数。
每只蝙蝠依据自身当前速度和当前位置与最优位置间的距离来更新其速度:
+1=++1(-)
(3)
式中,为蝙蝠在当前空间中的最优位置。
和粒子群算法一样,每只蝙蝠会进行位置的更新:
+1=++1
(4)
对于蝙蝠的第二种行为,蝙蝠会随机选取某个数,如果该数大于蝙蝠的脉冲频率,蝙蝠就会选择随机飞行,其描述随机行为的公式为:
=+
(5)
式中:代表搜索后的蝙蝠生成的新的解;代表搜索之前的最优解;是[-1,1]内的随机数;为该代的所有蝙蝠的响度的平均值。
位置更新完成后,蝙蝠会比较当前位置与之前位置的优劣,如果新位置更好,则飞行到新的位置,否则停留在原处,在飞行到新位置的同时,蝙蝠会更新自己的响度和脉冲发射率:
=
(6)
+1=(1-e-)
(7)
式中,,为常数。
2.2 多目标蝙蝠算法
在多目标函数优化问题中,目标函数之间是相互冲突的,只能进行折中处理,尽可能的都达到最优。在单目标优化问题中,可以通过大于或者小于这样的简单关系对可行解中的解进行评价,但在多目标优化问题中,由于多个目标函数的存在,只能得到折中解,因此需要引入Pareto最优的概念来对折中解进行评价。
∀∈(1,2,3,…,),()≤()∧∃∈(1,2,3,…,),()≤()
(8)
式中,为子目标函数的个数。
3)Pareto最优解集和前沿面。全部Pareto最优解的集合称为Pareto最优解集,对应的目标函数的集合称为Pareto前沿面。
在采用的多目标蝙蝠算法中,首先使用加权法将所有目标函数转化为一个目标函数,其转化公式为:
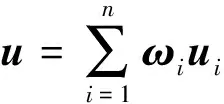
(9)
式中,权重向量是通过均匀分布产生的一组随机数,因此可以保证Pareto前沿面的多样性较好。然后与蝙蝠算法一样,对每只蝙蝠进行速度和位置的更新,以及响度和脉冲发射率的更新。
为了提高种群的搜索性能,在该多目标蝙蝠算法中,采用Pareto占优机制得到前沿面,通过前沿面得到的解集构成最优解的集合,该最优解的集合即为子目标函数折中解的集合。
3 内弹道优化过程与结果分析
3.1 内弹道优化过程
对于加农炮内弹道性能多目标优化问题,首先应该建立优化设计数学模型,并选取目标函数、约束条件、优化设计变量以及合理的优化设计方法等,然后通过建立的数学模型计算出目标变量值,最后利用优化设计模型得到目标变量的最优解。考虑到加农炮本身的作战特点、发射安全性和火药能量利用率等,文中将最大弹丸初速、最小炮口压力以及最大弹道效率作为待优化的目标。设计变量选择对内弹道性能影响较大的1/2火药弧厚、装药量及药室容积,考虑到发射安全性以及发射药燃烧的完全性等,将膛内最大压力和火药相对燃烧结束点作为约束条件。基于上述要求,得到的加农炮内弹道多目标优化模型为:

(10)
式中,为弹道效率,定义为:
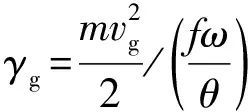
(11)
其中,=-1,为绝热指数。
为火药相对燃烧结束位置,定义为:
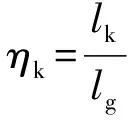
(12)
式中:为弹丸行程长;为火药燃烧结束位置。
将上述多目标蝙蝠算法与加农炮内弹道性能优化相结合,得到基于多目标蝙蝠算法的加农炮内弹道性能优化过程:
步骤1:设置初始参数,对蝙蝠种群位置进行初始化。
步骤2:基于3个目标函数,利用Pareto占优机制得到Pareto最优解集,并将炮口速度、炮口压力和弹道效率作为需要求解的目标函数,然后调用加农炮内弹道程序计算各个子目标函数值。
步骤3:依据式(3)和式(4)对蝙蝠进行速度和位置的更新,将更新后的个体位置与历史最优个体进行比较,选择将目标函数值最优的个体位置作为当前种群的最优位置。
步骤4:生成0~1之间正态分布的随机数,如果>,则参考式(5)选取一个新位置,否则蝙蝠随机产生一个新位置。
步骤5:假设蝙蝠个体当前位置优于种群当前位置,且满足<,则将步骤4产生的新位置作为种群的最优位置,否则将作为更新后的种群最优位置。
步骤6:若当前迭代次数大于最大迭代次数,则输出最优位置,否则返回步骤2。
步骤7:根据步骤6得到的最优位置,输出Pareto最优解集,进而得到一系列优化后的炮口初速值、炮口压力值和弹道效率值。
3.2 内弹道优化结果与分析
对于多目标蝙蝠算法,参考文献[15],设置种群规模为150,算法最大迭代次数为300,响度从1减小到0,响度衰减系数为0.9,脉冲频率在0~1之间变化。
利用多目标蝙蝠算法对该加农炮内弹道性能进行多目标优化,图2显示了在不同迭代次数下的子目标的变化趋势,图3为优化设计变量在不同迭代次数下的变化。由图2和图3可以看出:随着迭代次数增加,无论是子目标函数,还是优化设计变量,都得到了显著的改善。
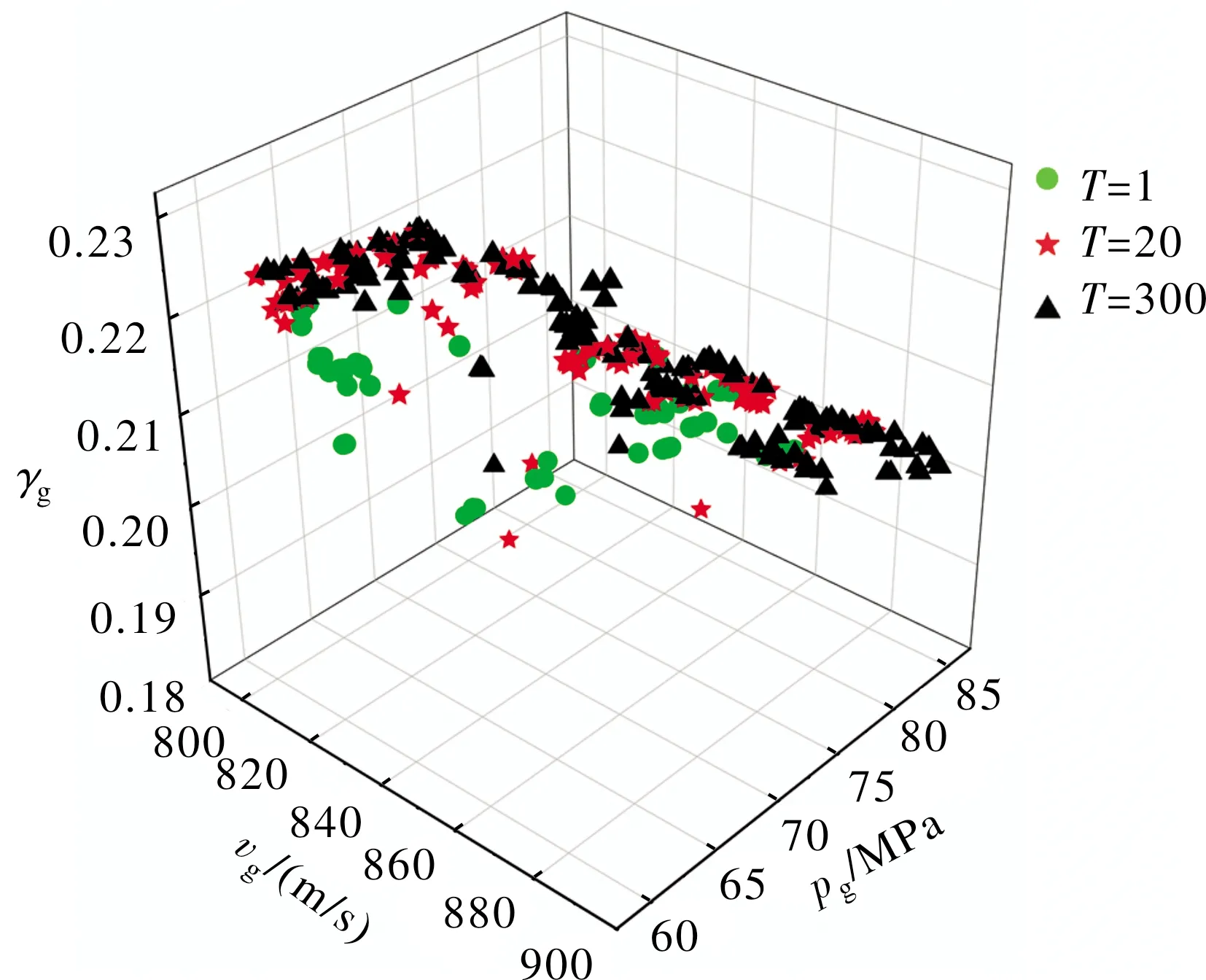
图2 子目标优化进程
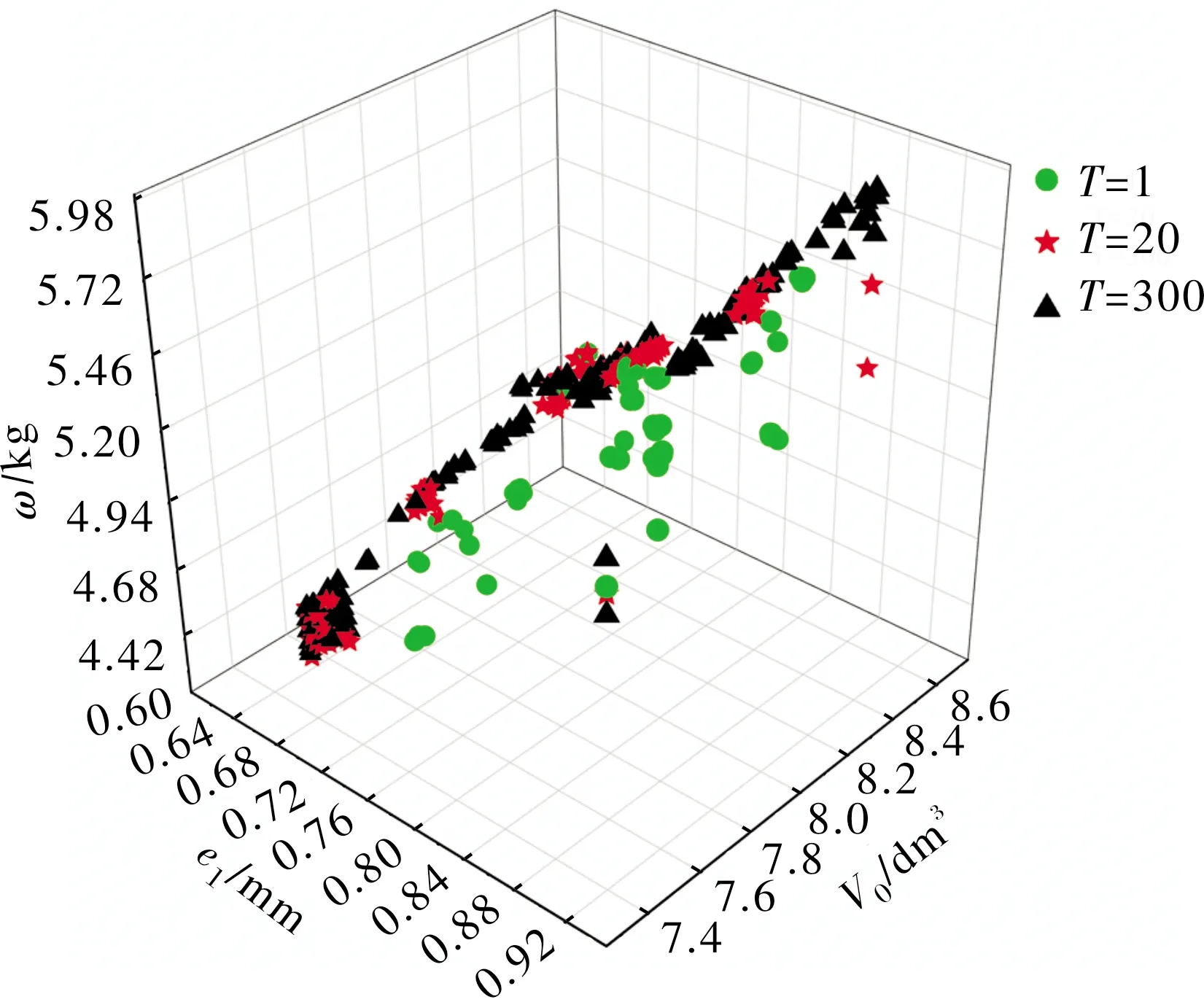
图3 设计变量优化进程
选择炮口初速、炮口压力和弹道效率这3个子目标,然后考察解集的分布以及子目标之间的关系,如图4所示。图4(a)描述了炮口初速和炮口压力之间的关系,由图可以看出,炮口初速随着炮口压力的增加而增加,且目标之间的相关性很高。图4(b)和图4(c)分别给出了弹道效率和炮口初速的关系以及弹道效率和炮口压力之间的关系,其中,弹道效率与炮口初速以及弹道效率与炮口压力之间存在着一定的负相关关系。原因在于,由弹道效率的公式可知,主装药量与弹道效率有最直接的关系,当主装药量增加时,弹道效率会减小,而随着主装药量的增加,火药释放的能量就更多,对弹丸做的功就变多,而无论是炮口初速还是炮口压力都会随着装药量的增加而增加,因此可以得到上述的结论。
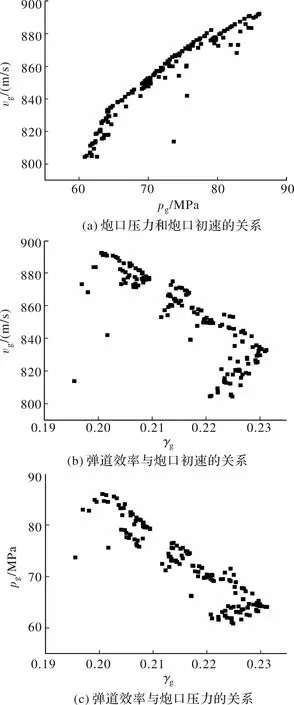
图4 子目标函数之间的关系
为了考察设计变量对目标函数的影响,图5、图6和图7分别给出了不同设计变量对炮口速度、炮口压力和弹道效率的影响,图中也显示了给定目标函数的不同变量的可行域。例如,图5(a)、图5(b)和图5(c)显示了管状药弧厚、药室容积和装药量3个变量两两之间对炮口初速的影响,由图5知,为了尽可能获得较大的炮口初速,需要将药室容积控制在8.2~8.5 dm,将1/2管状药弧厚控制在0.85~0.90 mm,将装药量控制在5.6~6.0 kg。
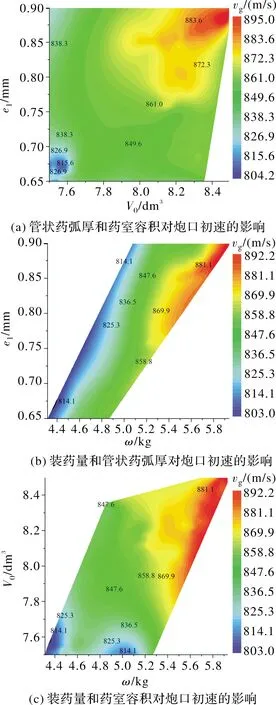
图5 优化设计变量对炮口初速的影响
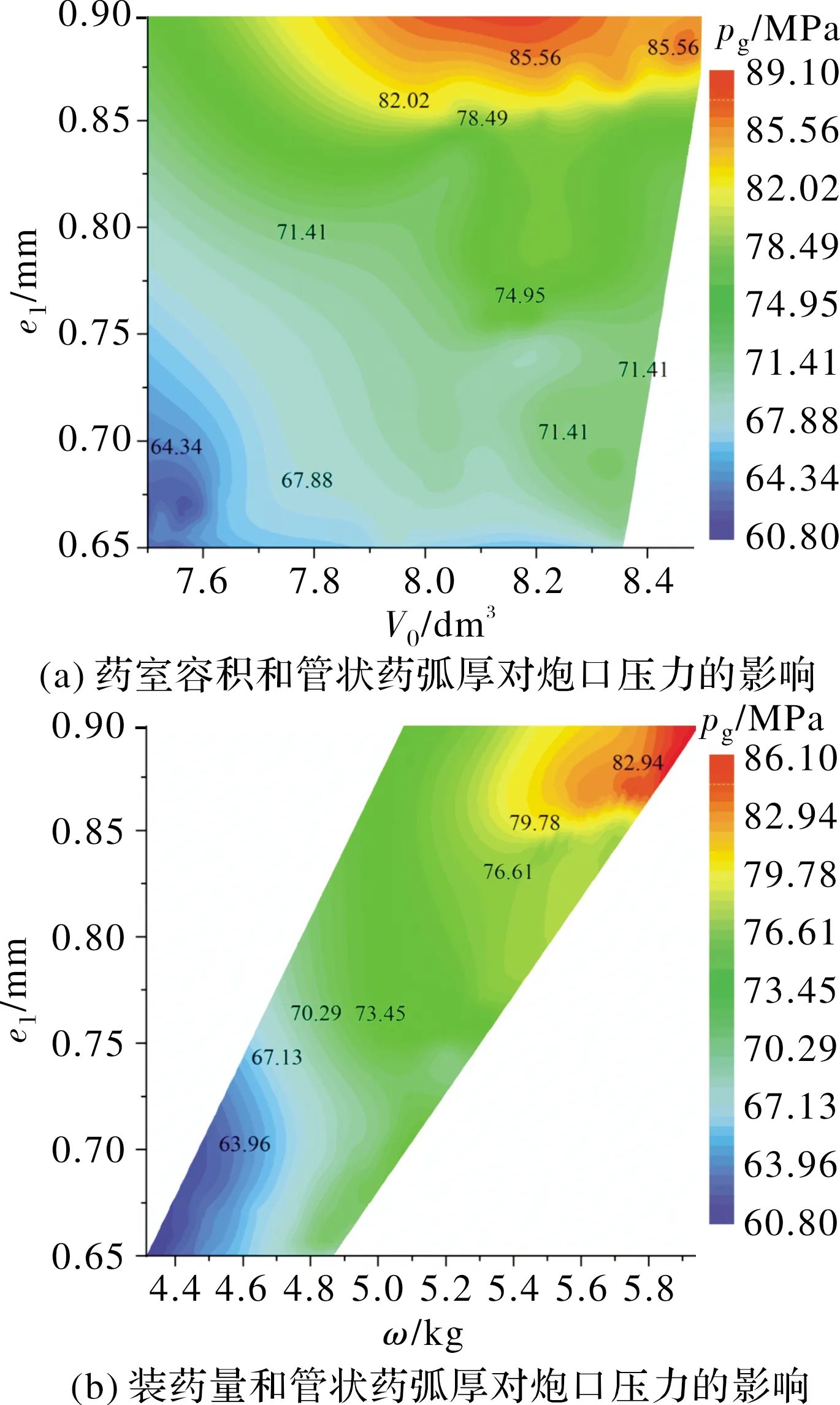
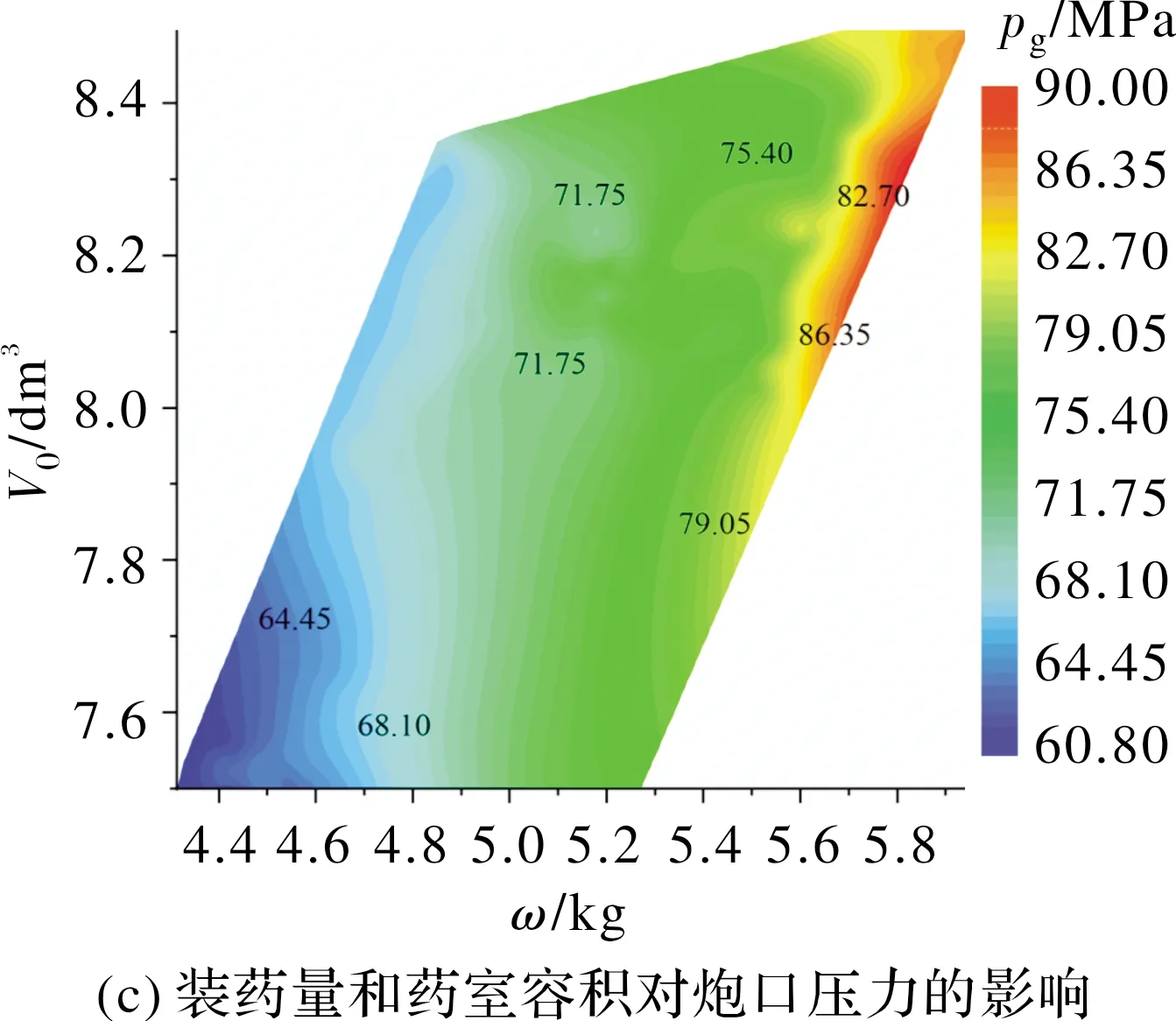
图6 优化设计变量对炮口压力的影响
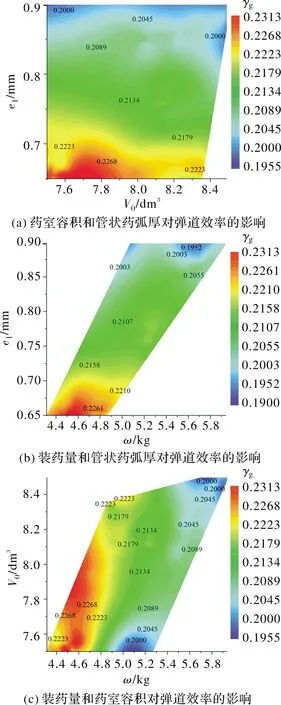
图7 优化设计变量对弹道效率的影响
对于火炮设计者来说,在实际应用中,通常考虑的是尽可能获得较大的炮口初速和较小的炮口压力,基于此,选择图4(a)中的一些特殊点,如图8所示。其中,点为多目标优化方案下的最大炮口初速点,点为综合考虑炮口初速和炮口压力下选择的较为合适的点。
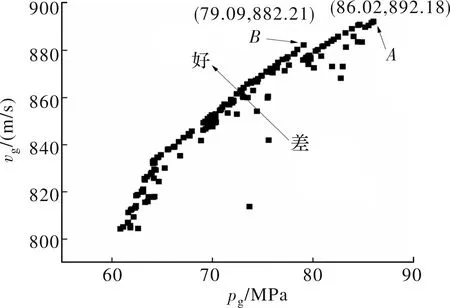
图8 炮口压力和炮口初速关系图
选择基于点下的优化方案,并与初始方案进行比较,如表2所示。
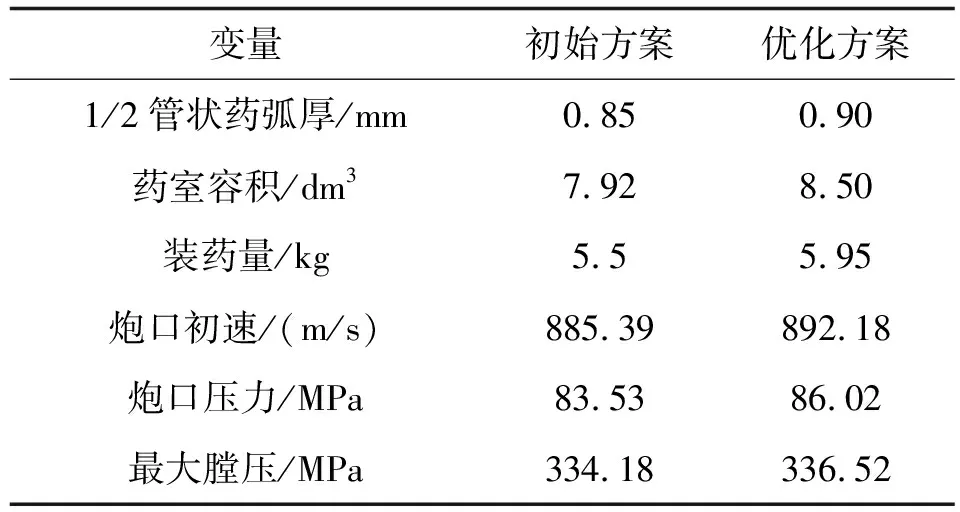
表2 优化方案与初始方案的比较
基于上述方案,得到的膛压和初速随时间的变化曲线如图9和图10所示。
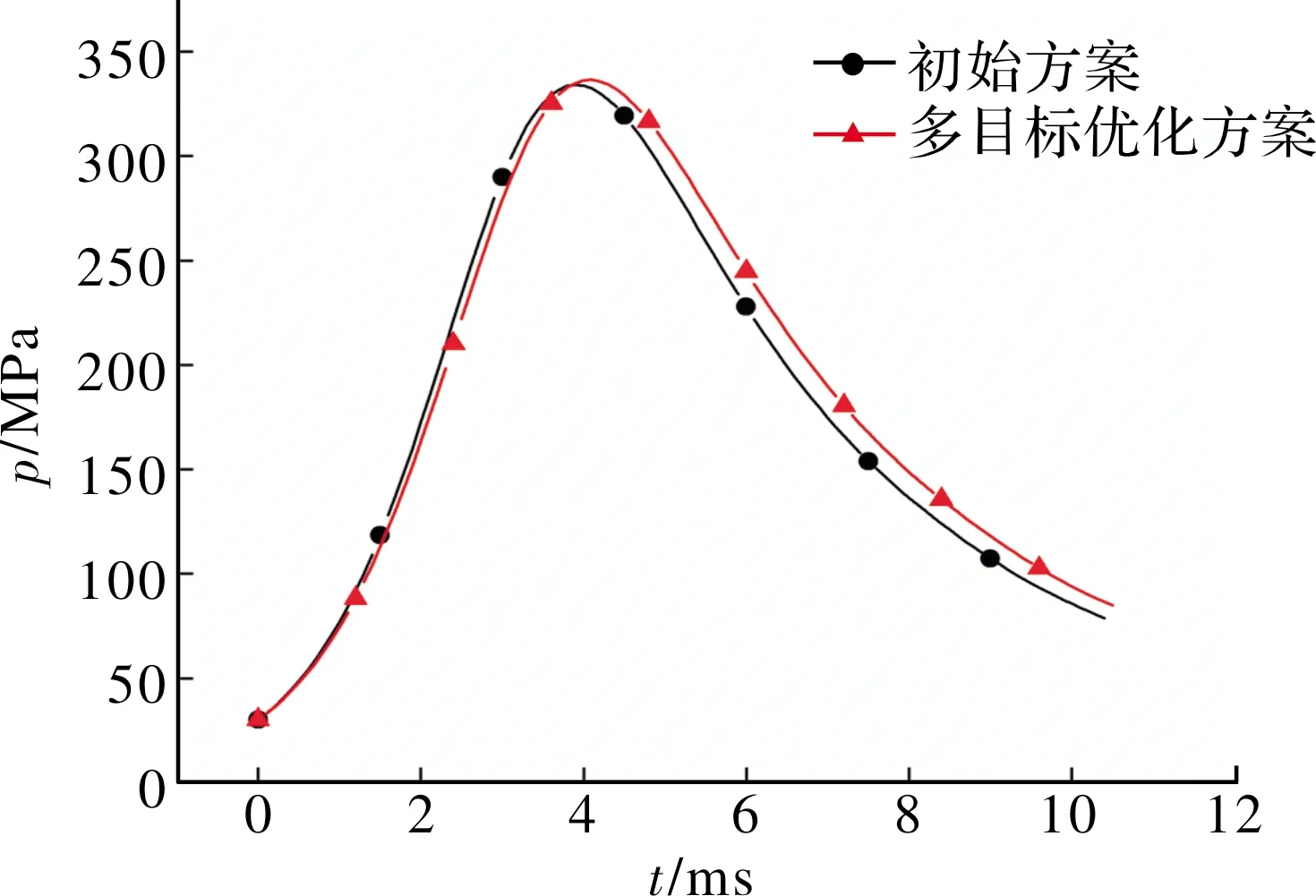
图9 p-t曲线
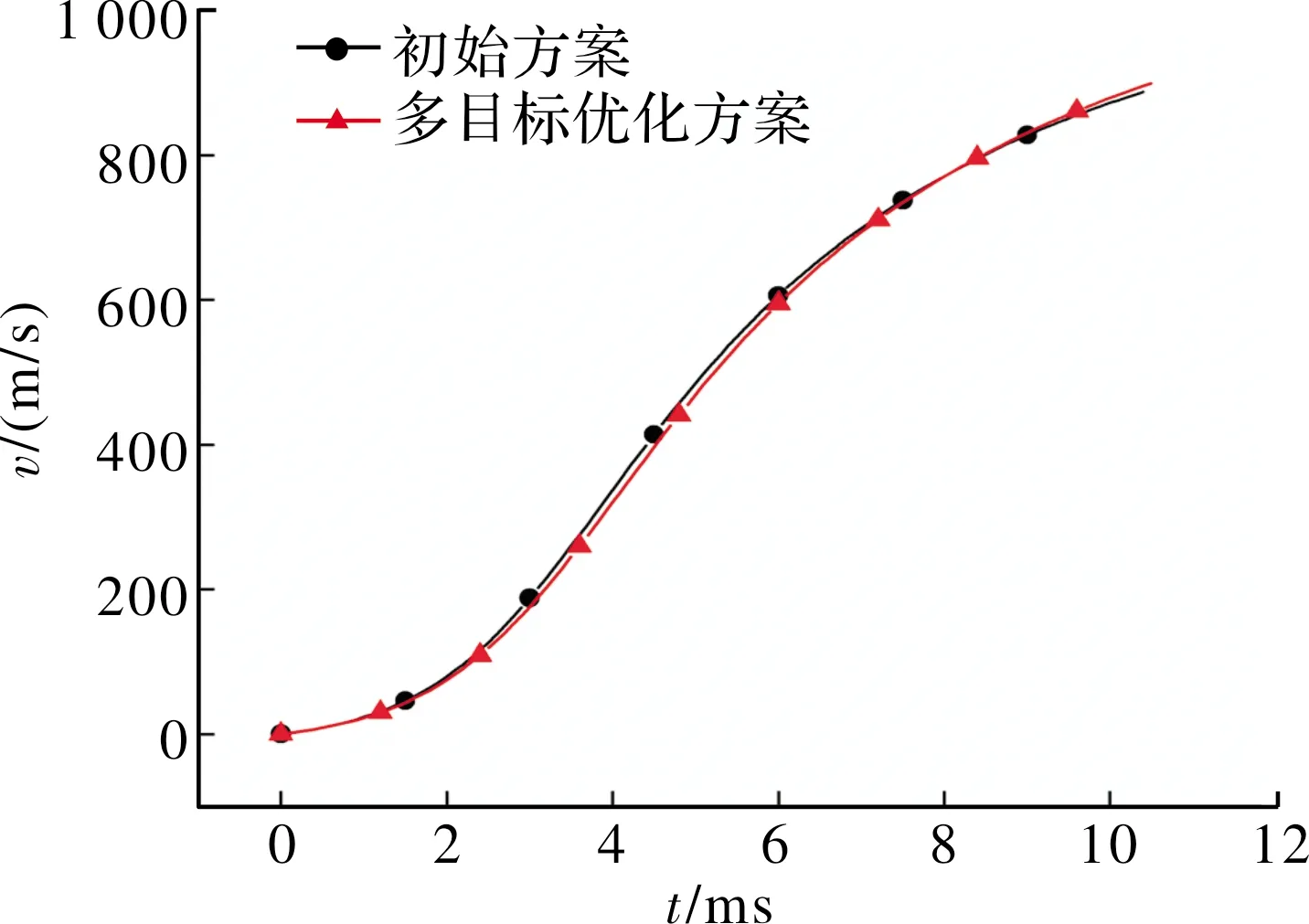
图10 v-t曲线
由图9和图10可知,多目标优化方案下得到的炮口初速更大,但该方案下得到的炮口压力也大,这进一步说明了在多目标函数优化问题中,几个目标函数是相互冲突的,一般不会出现所有目标函数都达到各自最优的情况,然而由图9和图10可以得到,多目标优化方案改善了-曲线的梯度,并推迟了最大压力点的出现,因此该多目标优化方案明显提升了内弹道性能以及提高了发射安全性。
4 结论
采用多目标蝙蝠算法对加农炮内弹道性能进行了多目标优化,通过选择将炮口初速、炮口压力和弹道效率作为拟优化的子目标,对该加农炮内弹道性能进行了真正的多目标优化,所得优化结果为一系列的Pareto最优解,可供火炮设计者根据需要进行选择。然后考察了不同设计变量对火炮内弹道性能的影响及各自目标函数下优化设计变量的可行域。然而,由于目标函数之间相互冲突,因此只能进行折中处理,但从多目标优化方案与初始方案的比较来看,得到的多目标优化方案明显提升了内弹道性能及火炮发射安全性,因此可以为今后加农炮的装药优化和提高加农炮发射安全性等提供一定的技术指导。

