基于Kappa制导的大空域变轨技术

王帅为,梁益铭，马季容，杨姝君，郑建强

(西安现代控制技术研究所，西安 710065)

0 引言

在现代海战中，作为主战武器的反舰导弹从发射开始，就处在敌方天、空、地各种传感预警系统的监视之下，敌方利用预警信息，就会引导其舰空导弹、“密集阵”火炮等进行拦截。为了提高导弹的突防概率，新型反舰导弹都采用机动变轨弹道。所谓变轨弹道,是指为了增加敌方对我反舰导弹的预测难度,并尽可能缩小敌方反应时间,提高突防概率,反舰导弹从发射开始,在燃料消耗、导航精度和作战时间允许的情况下实现的弹道轨迹变化。顾文锦等采用比例导引进行机动弹道设计，未考虑接近目标时攻角过大问题;庄益夫等采用变结构导引律进行机动弹道设计，但是由于引入符合项，存在抖振问题;毕开波等分析了导弹机动变轨的突防效能，但仅限于几种典型的机动变轨方式。

基于Kappa制导算法，文中提出一种大气层内机动变轨方法，可实现导弹任意方位的大空域变轨，且攻角变化缓慢，过载分布合理。

1 Kappa制导

Kappa控制算法应用于大气层内的中制导，也可解释为使导弹末速最大的中制导方法，这对于打击远距低高度目标是非常关键的。

用来表示弹目相对距离的垂直投影，视线角可以写成：

(1)

当较小时，视线角可表示为：

(2)

视线角速率可以表示为：

(3)

设导弹和目标不机动，接近速度近似为常值，即：

(4)

以向量表示预测拦截点的位置；向量表示导弹当前位置；为导弹速度；为期望的导弹末速，则比例导引可写成：

(5)

更一般的，可表示为：

(6)

式中：,为比例系数。

根据制导方程：

(7)

式中：为弹目距离;为导弹速度大小;为导弹质量;为=+分量确定的阻力;为推力;为升力系数。

为了保证末速最大，系数,的最优值分别为：

(8)

当→0，→0时:

(9)

由于制导指令生成于惯性系下，不存在比例导引视线系转序问题，只需给定终端速度方向矢量，即可实现导弹以任意方位攻击目标。

2 机动变轨方案

导弹采用虚拟目标变轨方式，给定一系列三维坐标点(,,),=1,2,…,,≠≠,将每一个坐标点看做一个虚拟目标，利用Kappa导引实时生成过载指令，形成一条光滑的轨迹，使其通过所有坐标点，并满足限制条件||≤max。

Kappa制导本质是通过抑制视线的旋转来达到命中目标的目的，若目标速度为零，则在命中点附近导弹速度方向将收敛于视线方向。记

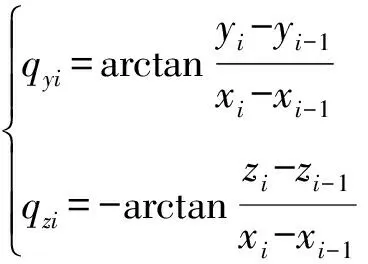
(10)

若Δ=+1-或Δ=+1-较大时，则切换目标后指令会有较大的跳变。考虑改变命中点的速度方向。

若三点共线时，即

(11)

则曲线在(,,)处的导数为：

(12)

若三点不共线时，设过三点的曲线为一空间圆，圆心为(,,),半径为。

由三点到圆心距离相等，可得：

消去，得到：

(14)

记为：

(15)

又圆心与三点共面，则：

(16)

展开记为：

+++=0

(17)

则：

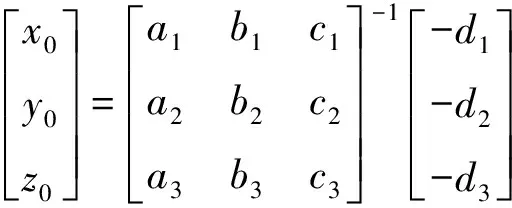
(18)

于是空间圆由以下两式确定：

(19)

对式(19)求全微分，得到：

(20)

则曲线在(,,)处的导数为：

(21)

记

(22)

则(,,)处速度的矢量可以表示为：

(23)

当导弹接近目标时，g会趋于零，制导指令将发散，导致切换指令出现大的跳变。给定一个切换距离，当弹目距<时，即切换到下一个目标。

(24)

式中：为当前时刻；为切换时刻；Δ为切换时间。

综合上述分析得到：

(25)

3 仿真验证

对提出的变轨制导律进行六自由度仿真，导弹方程组参考文献[7]。弹道形式为跃起弹道。设导弹速度为600 m/s，以m为单位给定5个目标点：(5 000,1 000,1 000)，(10 000,1 500,1 500),(20 000,1 000,1 000),(30 000,1 300,1 300),(40 000,0,0)。||<10°,||<10°,当弹目距<300 m时切换到下一虚拟目标，过渡时间Δ=2 s。仿真结果如图1～图4所示。

图1 轨迹

图2 弹目距

图3 攻角

图4 侧滑角

图1为导弹三维轨迹，可知导弹光滑的经过所有预设的虚拟目标点。图2为弹目距，导弹按照预设的切换条件切换4次，最终脱靶量几乎为零。图3、图4分别为导弹攻角和侧滑角，攻角最大为1.8°，侧滑角最大为1.3°，满足指标要求，且攻角变化缓慢，过载分布合理。

4 结论

研究了基于虚拟目标的大空域变轨技术。采用变轨弹道可以充分发挥导弹的机动能力，从而使拦截弹无法准确预测弹道，极大的提高导弹的突防效能。基于Kappa制导律设计了变轨弹道，通过空间圆确定虚拟目标点的速度方向，减小了目标切换引起的指令跳变。采用二阶平滑方式，使过载指令平滑过渡。该技术极大的提高了机动弹道设计的灵活性，且过载分布合理，有一定的工程应用前景。