基于分布式IMU的相控阵雷达运动补偿研究
陈 璞,吴旭华,李振威,冯鑫涛,张亚崇,程咏梅
(1 西安飞行自动控制研究所,西安 710065;2 西北工业大学自动化学院,西安 710129)
0 引言
相控阵天线具有指向性强、探测性强和可靠性高等优势,广泛应用于雷达系统中[1-2]。相控阵雷达通过控制信号的相位进而控制波束指向,而相位误差主要由阵元的位置误差所引起,因此相控阵雷达对安装位置有较高的精度需求。在相控阵雷达工作过程中,载体的振动和气流的冲击等都有可能导致阵面变形,引起阵元位置发生变化,并导致天线增益下降、波束指向精度降低,最终造成雷达性能的下降。上述问题对于蒙皮天线式相控阵雷达更为明显,安装于机翼时,由于飞机机翼并非刚体,在飞行过程中受气流、负载变化等因素的影响,机翼会发生一定程度的挠曲变形[3],将对雷达的性能造成较大的影响。Wang等从概率统计的角度分析了阵面随机位置误差对阵列天线性能的影响[4]。王从思等从机电耦合方面分析了弯曲等变形对电性能的影响,建立结构与电磁耦合模型,将阵面随机误差和阵面变形结合起来,分析了多种误差下对电性能的影响,并从阵面随机误差和阵面变形误差两方面分析对电性能的影响,比较了两者的不同[5-7]。以上研究均是关于阵面变形对雷达电性能的影响分析,未涉及对其进行补偿。
针对安装在机翼的蒙皮天线式相控阵雷达,文中提出一种基于分布式IMU的相控阵雷达运动补偿方法,在机翼上安装多个IMU,通过主节点、子节点间(与主惯导、子惯导含义相同)的相对导航解算和多节点信息融合监测机翼变形,进一步计算出阵面变形所引起的各个阵元的相位误差,并完成相位补偿,最终实现降低相控阵雷达的增益损失。
1 阵面变形对雷达电性能的影响
机翼上安装的相控阵雷达变形误差主要来自于初始随机安装误差和飞行中的机翼挠曲变形。矩形栅格相控阵阵元排列如图1所示,假设阵面共有M×N个阵元,沿x轴方向的阵元间距为dx,沿y轴方向的阵元间距为dy。根据远区观察方向与坐标系Oxyz的空间几何关系(见图2),假设目标所在方位(θ,φ)的方向余弦为(cosαx,cosαy,cosαz),则目标方向与坐标轴间的夹角和方向余弦的关系为[8]:
(1)

图1 矩形栅格排列阵的阵元排列示意图

图2 目标的空间几何关系
假设第(m,n)阵元(0≤m≤M-1,0≤n≤N-1)的位置偏移量为(Δxm,n,Δym,n,Δzm,n),指向偏转为(Δθ,Δφ),则该阵元相对第(0,0)阵元的相位差为[6]:
(2)

此时矩形栅格平面有源相控阵天线的方向图函数为[9]:
(3)
式中:fe(θ,φ)为半波振子作为辐射单元时的方向图函数。
将增益损失定义为[10]:
(4)
式中:f(θ,φ)为无误差时的方向图函数;fδ(θ,φ)为有误差时的方向图函数。
在现有的研究中,薄板仍是最接近实际机翼挠曲的理论模型,机翼挠曲主要考虑z轴方向的位移,机翼挠曲的平衡方程为[11]:
(5)
式中:q为机翼上的载荷;D为机翼弹性系统;LT为机翼长度;x为机翼横轴坐标值;s为对应的z轴挠曲位移。将任意子节点相对位置x,s代入后,就可以计算出q/(24D),因此每个主、子节点通过相对导航解算可获得一个机翼挠曲模型。
为分析不同挠曲程度下的影响,如图3所示,定义β为挠曲指数,反映机翼的挠曲程度。主节点在机翼根部,子节点n在机翼翼尖处。

图3 机翼挠曲形状
考虑挠曲变形和位置随机误差的共同影响,进行仿真分析,仿真10 GHz波段相控阵雷达,图4为不同挠曲指数和不同位置随机误差下带来的天线增益损失图,图中λ为波长,可以看出,增益损失远超出雷达性能所要求的0.5 dB[6],不符合相控阵雷达电性能的需求,因此需要对其进行补偿。

图4 机翼挠曲变形和误差下的增益损失图
2 基于分布式IMU的阵面变形补偿算法
精确的导航信息是满足现代载机高动态下任务设备空域稳定应用需求的关键所在[12]。在高动态应用场景中,当任务设备所在位置存在挠曲变形时,对任务设备的空域稳定存在较大的技术挑战[13]。其与传统导航应用需求的主要差异在于对短期姿态、姿态变化率、位置、位置变化率、速度的更新频率及精度等均有更高的要求。最有效的方法是通过传感器对任务设备的安装位置进行直接的运动测量,以量化导航信息的微小变化部分。雷达阵面的补偿对位置精度要求在cm级甚至是mm级。由于雷达阵面与机载主惯导间存在杆臂效应、安装误差、信号传输延时等误差因素,因此传统的主、子惯导间传递对准方法显然不能满足雷达运动补偿的使用要求[14]。通过分析,雷达阵面补偿本质上是一个对相对运动进行补偿的过程,只需要获得各个节点间位置的动态变化,便可以通过相对位置进行相位补偿[15-16]。因此,选用主节点为参考坐标系,首先进行主、子惯导间的相对导航解算[17],获得各个子节点相对于主节点的运动参数;其次通过多节点信息关联,获得实时的机翼结构形状;最后对机翼结构的方程进行积分,得到每个阵元的实时位置。
2.1 主、子惯导相对导航算法
主、子惯导间的相对姿态微分方程、相对速度微分方程、相对位置微分方程为[18]:
(6)

相对导航解算属于递推解算方法,在初始安装误差和惯性元器件误差等各种误差源的影响下,相对导航解算结果会出现累积误差。因此,需采用闭环反馈校正机制来对误差进行修正。这里以相对惯性导航误差模型为基础来建立卡尔曼滤波器的状态方程,考虑到陀螺仪漂移和加速度计零偏后,状态变量X为:

(7)

状态方程可写为:

(8)
式中,A,B,W的具体描述见文献[18]。
相对惯性导航的解算过程没有任何外界参考信息,因而给量测值的选择带来一定困难。考虑到机翼形状的约束,以相对挠曲误差为量测向量。量测方程为:
y=HX+v
(9)
式中:v为量测噪声。
量测矩阵H为:
H=[03×9I3×303×6]
(10)

图5 相对挠曲误差几何示意图

(11)
因此,通过式(11)可获得δRf的量测值,进而利用卡尔曼滤波基本原理,对状态变量进行最优估计。
在实际应用中,将挠曲分为高频挠曲和低频挠曲。对于高频挠曲,可以使用一阶滞后滤波等方法进行抑制[14]:
mn=(1-a)·mn-1+a·kn
(12)
式中:mn为本次滤波结果;mn-1为上次滤波结果,kn为本次采样值;权值a根据实际要求进行选择,取值范围为0~1。
对于低频挠曲,可以利用主、子节点间的相对姿态与相对位置的关系进行估计[14]:
(13)
式中:μf为挠曲变形角,由相对姿态解算所得。
2.2 多节点信息融合
由式(5)可知,每个主、子惯导均可以计算出一个机翼挠曲模型,机翼上安装有多个子惯导,因此可以进行多节点关联。联邦卡尔曼滤波已广泛应用于多传感器融合领域,具有精度高、配置灵活、计算量低和容错性好等优点[19-20],因此这里选用联邦卡尔曼滤波作为融合算法,将状态变量X进行扩展[21]:
(14)
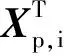
3 仿真结果
3.1 分布式IMU仿真
为验证相对导航算法的有效性,设计了飞行仿真轨迹,共计720 s,初始时北向速度为200 m/s,2 min内爬升5 700 m,然后匀速飞行0.5 min,接着6 min内航向转过360°,再匀速飞行0.5 min,最后2 min内俯冲下降5 700 m。主惯导由轨迹发生器得到,再叠加上挠曲变形角和挠曲位移得到子惯导的数据,以m为单位,主惯导位置为[0,0,0]T,子惯导共10个,安装于[1,0.5,0]T、[2,0.5,0]T、[3,0.5,0]T、[4,0.5,0]T、[5,0.5,0]T、[1,-0.5,0]T、[2,-0.5,0]T、[3,-0.5,0]T、[4,-0.5,0]T、[5,-0.5.0]T,主节点、子节点IMU噪声参数见表1~表2。考虑到机翼结构,这里只考虑纵向挠曲,挠曲位移跟飞行时间的关系用正弦函数来模拟,最大挠曲指数设置为5°[17]。

表1 陀螺仪参数

表2 加速度计参数
主节点与子节点n相对位置解算结果见图6,相对位置解算误差结果见图7。并由表3可知,经过多节点信息融合后的挠曲位移误差非常小,翼尖处的z轴方向挠曲位移仅为4.447 7 mm。

图6 主、子惯导相对位置解算图

图7 主、子惯导相对位置解算误差图

表3 相对导航解算RMSE
3.2 雷达电性能补偿仿真
仿真10 GHz波段相控阵雷达,阵元为9行33列矩形排列,其中天线的中心阵元(0,0)即第5行第17列阵元安装在机翼上[2,0,0]T,单位m,阵元间距为两倍波长,挠曲时相控阵雷达阵列排列图见图8。

图8 机翼挠曲下的相控阵雷达阵列图
经过多节点信息融合,可以实时计算出一条机翼形状,再对机翼模型的方程进行积分,可以解得每个相控阵阵元的实时位置,进一步对相控阵雷达的相位误差进行实时补偿。补偿前后雷达天线增益损失结果见图9,可以得出,经过补偿后,不同挠曲指数下增益损失均在0.2 dB以下,可以满足雷达电性能的需求。为更好的体现所提方法的性能,在挠曲指数为5°时,对补偿前后雷达方向图进行对比,见图10,可以看出补偿后的波束信号功率强,且波束指向精度大幅提高。

图9 增益损失补偿前后对比图(最大挠曲指数5°)

图10 挠曲指数5°时的方向图对比
4 结论
提出一种基于分布式IMU的相控阵雷达阵元相位误差补偿方法,通过主、子节点间的相对导航解算以及多节点信息融合的技术途径实时重建阵面结构,实现对每个阵元的相位误差补偿,从而降低了天线增益损失。实验结果表明,所提的技术方案对相控阵雷达进行实时运动补偿后,天线增益损失在0.2 dB以下,波束指向精度明显得到提高,这对相控阵雷达运动补偿具有重要的借鉴意义。在未来的工作中,还需深入探究相控阵雷达各阵元相位中心的相位误差与惯导误差之间的对应关系,以及如何通过分布式IMU进一步提升各阵元相位中心之间的相对关系,从而为改善相控阵雷达运动补偿系统的设计提供有价值的指导。

