基于GWR的住宅价格影响因素研究——以合肥市为例

鲍雅君,王依林，郭忠臣,2，王成洋

1.宿州学院环境与测绘工程学院,安徽宿州,234000；2.安徽理工大学土木建筑学院，安徽淮南,232001

改革开放以来，房地产市场得到了快速发展，城市地价呈现稳步上升趋势，住宅价格随之升高。地理加权回归模型是由英国地理学家Fotheringham在1998年首次提出，是一种全新的空间信息研究方法[1]。地理加权回归模型在各个领域得到了广泛运用[2]，其中大量学者在房地产价格方面研究中使用该模型。Yu等[3]以美国密尔沃基市的住宅价格为自变量，以住宅面积和周围环境为因变量通过运用地理加权回归模型和特征价格模型两种方法进行研究，得出GWR模型拟合效果优于特征价格模型；San[4]通过地理加权回归模型研究马拉西亚住宅价格影响因素，发现住宅价格的高低受到利率、失业率等因素影响。Zhang[5]运用GWR模型对宾馆价格进行分析，基于GWR模型的空间异质性特点，清晰阐述了不同地区对宾馆价格影响存在显著差异性；尹上岗等[6]借助地理加权回归模型对影响南京市住宅价格因素进行分析，得到住宅价格的主要影响因素及其作用程度；张明霞等[7]选取2018年7月份南昌市城区住宅小区作为实验对象，运用地理加权回归模型和GIS空间分析方法进行研究，得出区位特征和重点中学对房价的影响作用最大；刘贵文等[8]以重庆市市辖区普通商品住宅小区均价为研究对象，利用GWR和OLS两种方法对区域因素、一般因素和个别因素三个层次影响因素进行对比，得出GWR模型的拟合效果显著优于OLS模型，证实了GWR模型是研究空间异质性影响因素的有效方法；徐晶鑫等[9]对南京市住宅小区社区属性、交通属性和附近相应配套设施三方面价格影响因素进行分析，得出相对于OLS模型而言,GWR模型结果更加准确；余岷燚[10]以杭州市写字楼租金为研究对象，对其内部特征和外部特征两个方面进行研究，结果表明地理加权回归模型相对于特征价格模型在拟合方面表现更加优异。

综上所述，住宅属于典型的空间异质性商品，即功能形式和参数在研究区域内不同地方的表现是不一致的，但是在区域的局部变化是一致的。将地理加权回归方法运用到住宅价格影响因素分析上，可以更好地阐述和解释变量与被解释变量间的关系[11]，因此本文基于GWR模型对合肥市住宅价格影响因素进行分析，以期为城市规划和房地产行业发展提供借鉴。

1 数据与方法

1.1 研究区概况

选取合肥市市辖区为研究区(图1)，合肥作为安徽省省会，是安徽省经济、政治、文化中心。鉴于近几年来合肥得到了快速的发展，对其住宅价格及影响因素的研究不仅可以公正客观地反应住宅价格的影响因素，还可以为其他城市以及买房者和房地产开发商提供一定的参考。

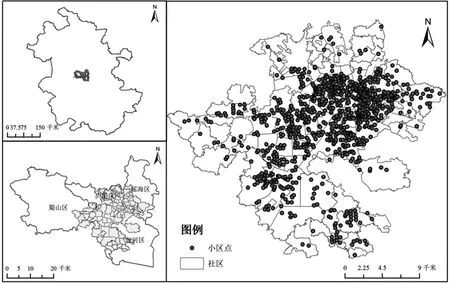
图1 研究区概况

1.2 数据来源

研究以2018年12月为时间截面，利用网络爬虫工具从搜房网(http://nanjing.fang.com/)上抓取合肥市市辖区内所有住宅数据，整理成表格。主要包括小区的属性数据、空间数据。获取数据后对其进行3轮清洗校正。首先，整理数据并统计分析，剔除经济适用房、LOFT公寓、别墅等价格波动较大的特殊房源，只选取合肥市城区的商品房、住宅小区作为研究对象；其次借助百度地图对数据进行校正，剔除错误数据；最后将搜房网与百度地图数据进行对比，校正并补全残缺数据。

1.3 空间插值法

利用空间插值法获取住宅小区点的空间属性特征[12]，常见的空间插值法有克里金插值法、反距离权重法(IDW)、临近法等方法。反距离权重法是以插值点与样本点之间的距离作为权重进行插值，离差值点越近，权重越大，离插值点越远，权重越小[13]。本文采取反距离权重法对合肥市住宅小区数据进行插值分析。

1.4 空间自相关分析

空间自相关是指在同一区域内同一属性要素在不同位置上存在相互依赖性[14]，进行空间自相关分析目的，是为了检验研究区内的数据在空间上是否存在聚集效应和空间异质性。由于合肥市住宅小区数据是以离散点的形式分布在合肥市市辖区内，所以本文利用空间自相关分析来检验相邻数据点之间是否存在相关性[15]。空间自相关分析包括全局自相关和局部自相关两种，全局自相关通常用莫兰指数(Moran′s I)表示，数值的正负代表数据在空间上的正负相关性，为了进一步得到更加精确的相关性，文章使用聚类和异常值分析工具(Local Moran′s I)进行局部相关性检验[16]。

1.5 地理加权回归模型

地理加权回归模型是一种用来揭示数据时间非平稳性与空间非平稳性的有效研究模型，能够提高对时空数据演变规律的认知，增强对时空数据的分析能力。模型表示如下：

(1)

其中，(ui,vi)为第i个采样点的坐标；βk(ui,vi)表示第i个采样点上的第k个回归参数，是地理位置的函数。计算方法如下：

βk(ui,vi)=[XTW(ui,vi)X]-1XTW(ui,vi)y

(2)

其中，X为自变量矩阵；W(ui,vi)为空间权重矩阵，它用来表述位置与参数估计之间的相关性。通常权重用高斯距离权重或双重平方距离权重两种函数表示，分别如下:

(3)

其中h为带宽，dij为位置间的距离。

2 合肥市住宅价格空间分布格局

2.1 合肥市住宅价格概况

研究获取合肥市住宅均价为14 508 元/m2。其中天鹅湖周围的住宅价格最高，超过20 000 元/m2；瑶海区北部以及庐阳区北部的局部地区价格则低于10 000 元/m2。从图2可知，合肥市房价呈现两边低中间高的趋势，从西向东，价格先增后降，从南到北，价格呈现明显的“倒U”型，综合两边的趋势来看合肥市住宅价格呈现城市中央高边缘低格局。

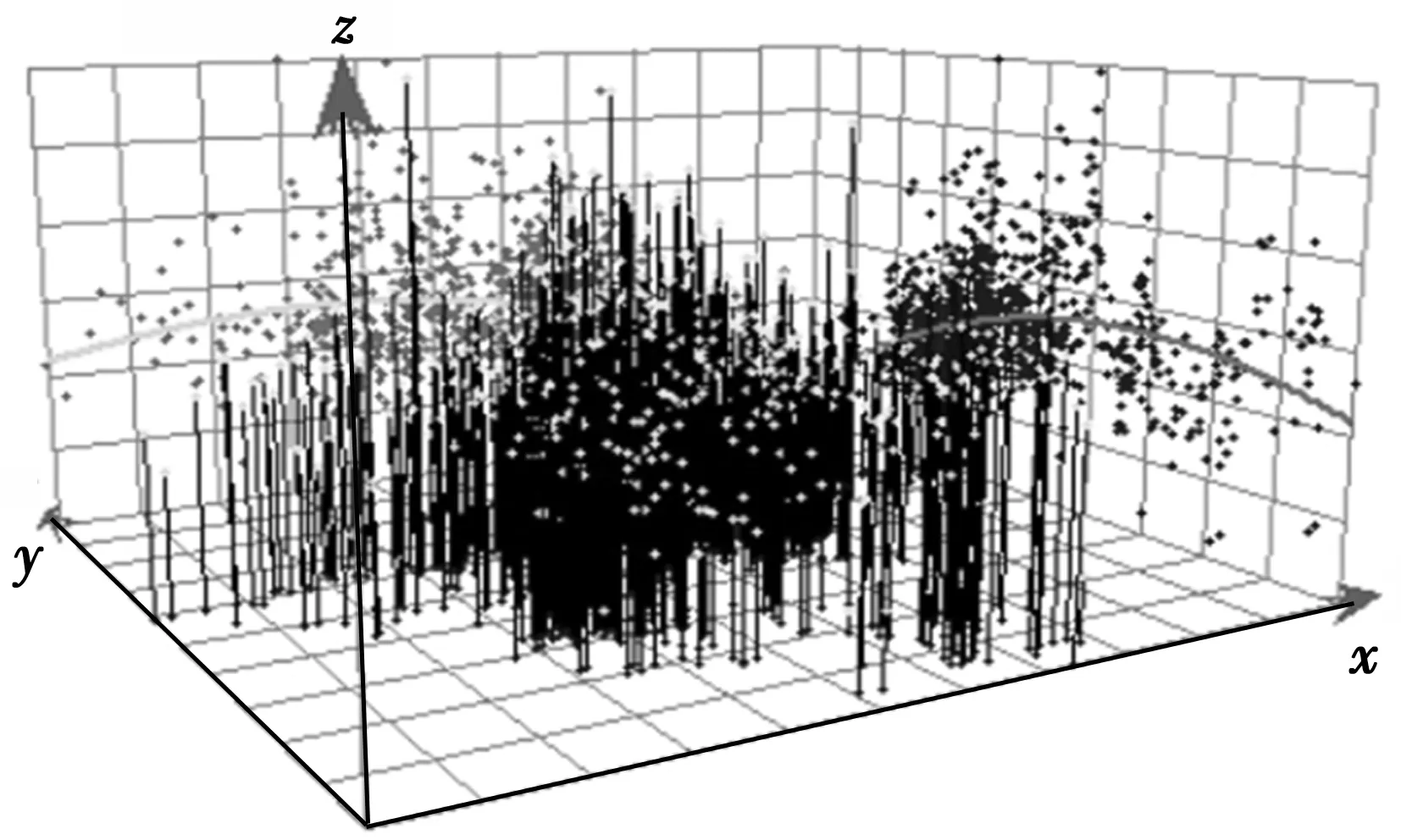
图2 合肥市住宅价格趋势图

2.2 空间自相关分析

对住宅价格数据进行全局自相关分析，莫兰指数为0.312 014，Z得分为33.9，P值为0.00，表明住宅价格呈现显著空间聚集性。进行局部空间自相关分析，由图3可以看出，合肥市住宅价格较高的地方主要集中在天鹅湖附近和蜀山区北部到庐阳区南部之间以及包河区南部的滨湖新区周围；而住宅价格较低的位置集中在瑶海区南部，瑶海区南部是合肥市的老城区，交通相对于新城区而言较为阻塞，尤其靠近火车站附近，人员流通密集交通阻塞情况更为严重，因此该区域住宅价格较周围更低廉。

图3 局部自相关结果图

2.3 合肥市住宅价格空间分异格局

合肥市住宅价格以天鹅湖为中心，房价随着距离增加呈现衰减趋势(图4)。天鹅湖中心位置价格处于最高点，其次天鹅湖周围、庐阳区护城河内以及滨湖新区。这片区域内城市绿化率较高、商业集中，人们生活更加便利，因此该区域住宅价格处于中高水平。瑶海区南部是老城区，交通以及绿化有所不足，同时存在火车噪音以及灰尘较重等情况，该区域住宅价格处于较低水平。

图4 住宅价格空间分异格局

3 合肥市住宅价格因素分析

3.1 影响因素量化及模型构建

从合肥市住宅的区位属性、邻里环境、建筑特征三方面来归纳住宅价格影响因素[14-17]。其中住宅小区到地铁站、商场、学校(中小学)距离作为区位条件，将住宅小区到医院的距离和小区周围1 km半径范围内银行、超市的数量作为邻里环境参数，物业费、绿化率、容积率、房龄作为建筑特征(表1)。

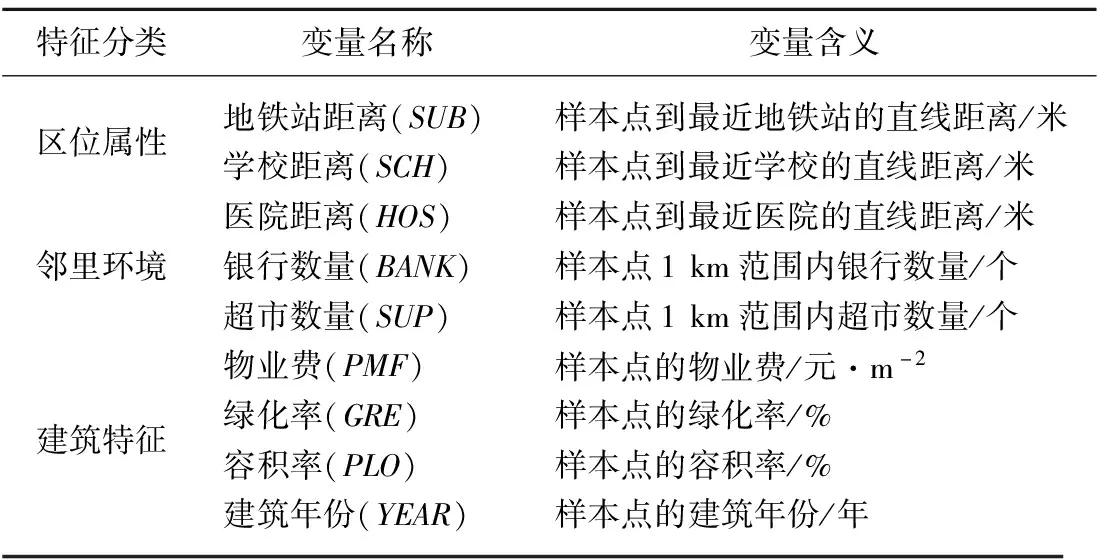
表1 特征变量的描述

3.2 空间回归模型比较

表2反映出物业费用、绿化率、医院距离、1 km范围内银行的数量与房价有正相关性，容积率、小区距地铁站、学校、景区的距离以及1 km范围内超市的数量与房价有负相关性。所有变量的方差膨胀因子(VIF)均小于7.5，表明不存在多重共线性；物业费用、绿化率、房龄、小区距地铁站、学校、医院的距离以及1 km范围内银行和超市的数量通过了5%显著性检验；T统计值显示各系数在统计学上是有意义的[8]，Koenker(BP)统计量观测值为49.485，自由度观测值为0.000，具有统计学上的显著性，说明数据存在空间不稳定性或有异方差的存在。

表2 OLS模型结果统计表

容积率没有通过显著性检验，因此剔除容积率这一影响因素用其他影响因素构建地理加权回归模型，得到模型如下：

yi=β0(ui,vi)+β1(ui,vi)xi1(SUB)

+β2(ui,vi)xi2(SCH)+β3(ui,vi)xi3(HOS)

+β4(ui,vi)xi4(BANK)+β5(ui,vi)xi5(SUP)

+β6(ui,vi)xi6(PMF)+β7(ui,vi)xi7(GRE)

+β8(ui,vi)xi8(PLO)+β9(ui,vi)xi9(YEAR)+εi其中，yi表示样本点i位置的房价，xij表示各自变量在i点的观测值，βj(ui,vi)表示在样点的i的系数值。地理加权回归分析结果如表3所示，物业费用、1 km范围内超市和银行数量以及房龄是影响合肥市住宅价格的主要因素，距离地铁站、学校、医院距离影响程度相对较小。

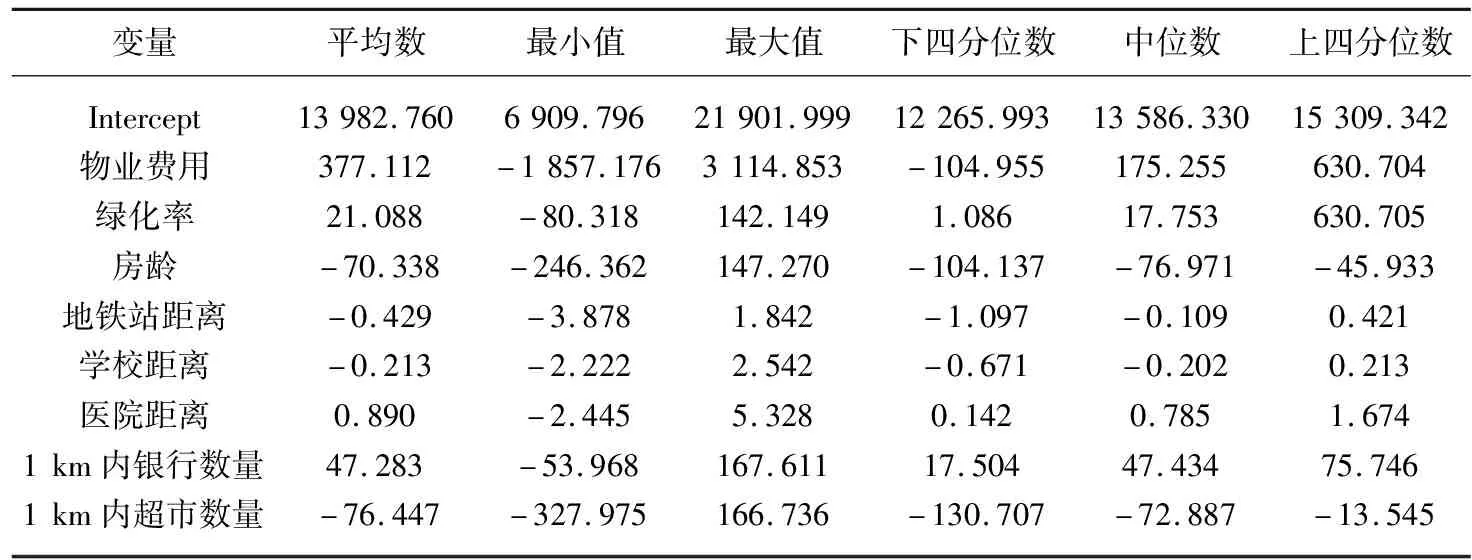
表3 GWR模型回归系数统计表

对比OLS模型和GWR模型结果(表4)，OLS模型校正R2为0.17，GWR模型校正R2为0.50，表明GWR模型比OLS模型对住宅价格的解释能力提高了33.30%；AICc值，GWR模型比OLS模型收敛了440.228，表明GWR模型的拟合效果优于OLS模型。因此，GWR模型比OLS模型更适用于合肥市住宅价格及其影响因素研究。

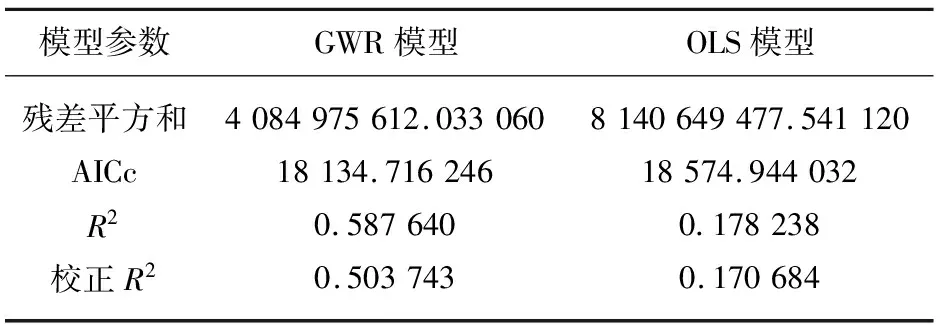
表4 GWR和OLS模型对比

3.3 住宅价格影响因素分析

物业费用对于合肥市住宅价格的影响最大，从图5(a)可以看出物业费与住宅价格呈现正相关，当物业费每提高1元/m2时住宅价格随之提高377.11元/m2，居民越来越看重优良的治安环境和小区各项服务，合肥市老城区绝大部分小区建设年份较早，物业费低廉，因此该区域物业费用对小区的住宅价格影响没有蜀山区南部新建小区的影响大。

小区的绿化可以让居民身心愉悦，同时植被还可以降低空气中的灰尘以及路边的噪音，由图5(b)可得绿化率越高住宅价格越高，其中在天鹅湖周围绿化率对住宅价格的影响最显著，而在老城区附近，有古逍遥津、杏花公园、包公园等景区，公园绿地可达性较好，因此该区域内小区绿化率对住宅价格提升作用不大。

房屋具有一定的时效性(见图5(c))，随着小区建成时间越长，小区内的公共设施以及环境也会有所下降，对于住宅价格会产生一定的副作用，房龄与住宅价格呈反比，房龄越小住宅价格越高，天鹅湖南部以及滨湖新区的小区房龄较低，住宅价格较高，而庐阳区南部、瑶海区南部以及董铺水库周围属于合肥市老城区，小区建成年代较早，价格相对较低。

城市轨道交通具有快速便宜等优势可以方便居民的出行。本文选取合肥市轨道交通1号线和在建的2号线为研究对象，从图5(d)可得距轨道交通1号线和2号线的距离与住宅价格有负相关，在郊区影响程度相对较高，而在火车站附近，住宅价格受其影响程度较小，是由于火车站周围交通便捷，地铁能到达的区域相对较少，因此未能体现出优势。

图5 各影响因素对住宅价格的影响

图6(a)显示距中小学距离对住宅价格有提升作用，合肥市优等中学主要集中在包河区北部和瑶海区南部，因此该区域内学校可达性对房价的影响程度较其他两区更为显著。

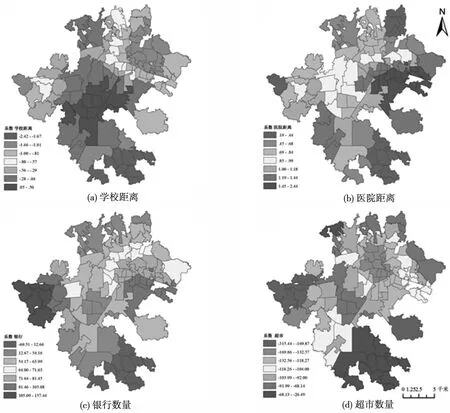
图6 各影响因素对住宅价格的影响

图6(b)体现了包河区北部小区到医院的距离对住宅价格的影响呈正向作用，离医院的距离越远住宅价格越高，这是由于该区域内三甲及综合性医院较少，而普通医院带来的环境污染和噪音弊端大于利端；同时，庐阳区南部、蜀山区北部和滨湖新区三甲及综合性医院相对较多，医院产生的负面影响远小于就医便捷优势，因此该区域内越靠近医院住宅价格越高。

图6(c)可以看出,银行对住宅价格有提升作用。由表3可得，1 km半径范围内每增加1家银行，住宅价格随之提升47.28 元/m2，1 km范围内银行数量越多,区域商业越繁华，金融价值越高，住宅价格越高。

由表3可得1 km半径范围内超市的数量与住宅价格呈负相关，每增加1个超市，住宅价格降低76.45元/m2。图6(d)可以看出，超市对住宅价格有显著负向作用，在合肥市老城区内消极影响显著大于滨湖新区，这是由于老城区分布有主流大型超市，而小型零售超市的数量增加会产生同质现象，因此许多小型零售超市选址在远离大型超市的区域，这样导致老城区商业用房存在资源浪费的情况，从而令整体住宅价格较郊区有所下降。

4 结 论

本文选取合肥市市辖区作为研究区，从区位属性、邻里环境和建筑特征三大方面选取八个要素，通过构建地理加权回归模型对其住宅价格影响因素及其作用程度进行分析，得到以下结论：

(1)合肥市住宅价格在空间上呈现显著集聚性。整体上，住宅价格的可以分为高中低三大板块，分别是以天鹅湖为中心的政务区高价板块，以滨湖新区与庐阳区南部组成的中等价格板块和以合肥市瑶海区北部与距商圈较远区域组成的低价板块。天鹅湖附近是合肥市的住宅价格峰值区域，超过20 000元/m2；三孝口、芜湖路、滨湖新区以及万达广场周边住宅价格处于16 000元/m2到19 000元/m2之间；住宅价格较低的地方分布较广，主要位于合肥市郊区以及远离大型商场的地方，价格一般位于10 000元/m2左右。

(2)合肥市住宅价格影响因素中，物业费用、1km范围内超市和银行数量以及房龄为主要因素，各影响因素作用程度为：物业费用>超市数量>房龄>银行数量>绿化率>医院距离>地铁站距离>学校距离。

(3)住宅价格具有空间异质性，在住宅价格影响因素分析中GWR模型相较于OLS模型更适用。对比两种模型，OLS模型校正R2为0.17，GWR模型校正R2为0.50，GWR模型比OLS模型对住宅价格的解释能力提高了33.30%，而AICc值GWR模型比OLS模型收敛了440.228，表明GWR模型的拟合效果要优于OLS模型。