一类平坦半环生成的簇

高子东,任苗苗

(西北大学数学学院,陕西 西安 710127)

1 引言和预备知识

设 V是同型代数作成的类.若 V对子代数,直积和同态像封闭,则称其为簇.由Birkhoff定理可知,一个同型代数类是簇当且仅当它是等式类,即满足某个恒等式集合的代数的全体.若簇V可由有限个恒等式确定,则称V是有限基底的,否则称V为非有限基底的.簇的有限基底问题是问它是否为有限基底的,该问题是簇的核心问题之一.设K是一些同型代数作成的类,用V(K)表示由K生成的簇,即包含K的最小的簇.若K中只有一个成员A,则简记为V(A).由Tarski定理可知,V(K)=HSP(K),其中H,S,P分别是同态像,子代数和直积类算子.

设(Ai)i∈I是一族同型代数,A是的子代数.若对于任意j∈I,用

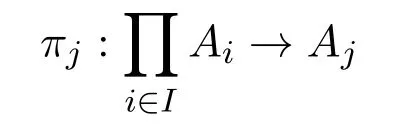
表示自然投射,均有πj(A)=Aj,则称A是 (Ai)i∈I的次直积.如果代数A只有平凡的次直积分解,即对于任意一族同型代数 (Ai)i∈I,A是 (Ai)i∈I的次直积蕴含着存在i∈I,使得AAi,则A被称为次直不可约的.若A是非平凡的代数,则A是次直不可约的当且仅当它有最小的非平凡同余.由文献[1]知,簇V的每个成员都可表示为它的一些次直不可约成员的次直积.这表明簇V完全被它的次直不可约成员所确定.因此,研究簇的次直不可约成员是簇的又一核心问题之一.

定义 1.1[2]设S是半群,A是S的任一非空子集.若AA⊆A,则称A为S的子半群,记作A≤S.若AS,SA⊆A,则称A为S的理想,记作AS.

设I是半群S的理想.则ρI(I×I)∪1S称为S上(由I确定)的Ress同余[3].其对应的商半群为

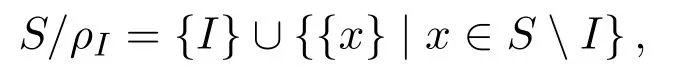
简记为S/I.容易验证,I是商半群S/I的零元,因此也可将S/I视为(SI)∪{0}.反之,则有如下命题:

命题1.1设S是含0的半群.若S上有同余ρ=(0/ρ×0/ρ)∪1S,则I0/ρS,进而ρ=ρI是半群S上的Ress同余.

证明设a∈0/ρ,s∈S.由aρ0,sρs,且ρ是S上的同余,可得

asρ0s=0,saρs0=0.

也即as,sa∈0/ρ.这表明I0/ρS,进而ρ=ρI是半群S上的Ress同余.

定义 1.2[2]设S是含0的半群.若对于任意a∈S,存在n∈N,使得an=0,则称S为nil-半群.

下面将给出nil-半群的0-极小理想[2]的刻画:

命题 1.2设S是nil-半群.若I是S的0-极小理想,则|I|=2.

证明任取a,b∈I{0}.由I的 0-极小性可知,S1aS1=S1bS1.故存在x,y,u,v∈S1,使得b=xay,a=ubv.因此

a=(ux)a(yb)= ···(ux)na(yb)n= ···.

结合S是nil-半群以及a0可知,x=y=u=v=1.这表明a=b.故|I|=2.

定义 1.3[2]设S是含0的半群.若满足:

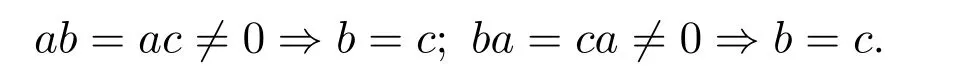
则称S为0-可消半群.

在下一节中,将讨论0-可消半群与平坦半环的关系.下面介绍半环的一些基本概念:

定义 1.4[2]设 (S,+,·)是(2,2)型代数.若满足:

(1)(S,+),(S,·) 是半群;

(2)(a+b)c=ac+bc,c(a+b)=ca+cb,∀a,b,c∈S,则称 (S,+,·)为半环,简记为S.

若半环S满足

a+b=b+a,a+a=a,∀a,b∈S,

则称S为加法幂等元半环,简记为ai-半环.

对于ai-半环S,定义偏序关系如下:

(∀a,b∈S)a≤b⇔a+b=b.

容易验证,(S,≤)是(上)半格,因此ai-半环也被称作半格序半群.

定义 1.5[3]设S是半环,A是S的任一非空子集.若A≤(S,+)且A≤(S,·),则称A是S的子半环,记作A≤S.若A(S,+)且A(S,·),则称A是S的理想,记作AS.

近二十年来,ai-半环簇的研究是非常活跃的[3-15].文献[11-12]研究了x2≈x确定的ai-半环簇.文献[3]给出了第一个非有限基底的有限ai-半环的例子.文献[5]给出了恒等式xn≈xm确定的ai-半环簇的自由对象的模型.文献[6]证明了若ai-半环满足恒等式xn≈x,则它的乘法导出是正则纯正密码群.文献[7-8]证明了满足恒等式x3≈x的ai-半环簇共有179个,且这些簇都是有限基底的.文献[10]研究了所有二阶ai-半环生成的簇,证明了它的子簇格是64阶的布尔代数.文献[13]研究了三阶ai-半环的有限基底问题.在上述文献的基础上,本文将主要研究次直不可约的平坦半环,以及一类平坦半环生成的簇.给出次直不可约的nil-平坦半环的一些等价刻画,证明当n≤3时,平坦半环S(x1x2···xn)均是有限基底的.

2 次直不可约的 nil-平坦半环

定义 2.1[1]设S是含乘法零元的半环.若其加法导出(S,+)满足:

则称S是平坦半环.

为了方便起见,将上述的“加法”称为 flat加法.容易验证,平坦半环S是一类特殊的ai-半环,其乘法零元亦是加法零元,且当|S|≥2时,(S,≤)是高度为1的半格.下面的引理将说明平坦半环与0-可消半群之间的关系:

引理 2.1设S是平坦半环,则其乘法导出 (S,·)是 0-可消半群.反之,对于任一0-可消半群(S,·),都可以定义 flat加法,使得(S,+,·)成为平坦半环.

证明设S是平坦半环.任取a,b,c∈S,若ab=ac0,则ab+ac=a(b+c)0,因此b+c0,故b=c.同理可知,由ba=ca0亦可推出b=c.因而,(S,·)是 0-可消半群.

反之,设 (S,·)是 0-可消半群,定义上述 flat加法.下面只需验证乘法 “·”对加法“+”具有左右分配律即可.任取a,b,c∈S:

(i)若b=c,则a(b+c)=ab=ab+ac.

(ii)若bc,则a(b+c)=a0=0.断言ab+ab=0,否则ab+ac0,进而ab=ac0,再由S的0-可消性可知,b=c,矛盾.因此,a(b+c)=0=ab+ac.

综上所述,a(b+c)=ab+ac.同理可知,(b+c)a=0=ba+ca.因此,(S,+,·)是平坦半环.

上述引理说明,平坦半环与0-可消半群具有一一对应的关系.因此构造具体的平坦半环时,只需构造出0-可消半群,然后在此基础上赋予 flat加法即可.容易验证,对于任意可消半群S(或更为特殊的自由半群,群等),直接添加零元,即可得到0-可消半群S0.但这并不意味着0-可消半群都是通过这种方式得到的,例如null-半群S(也即满足S2={0}的半群).下面将介绍一类重要的0-可消半群:

命题 2.1设W是自由半群X+的任一非空子集.令

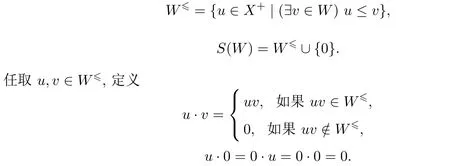
则 (S(W),·)是 0-可消半群.

证明直接验证可知,(S(W),·)满足结合律以及 0-可消性.为了揭示 (S(W)与X+0的关系,取I=X+S(W),则有IX+0且X+0/I～=S(W).而X+0是 0-可消的,进而容易验证X+0/I亦为0-可消半群,因此S(W)也是0-可消半群.

赋予 flat加法可知,(S(W),+,·)是平坦半环,简记为S(W).当W={w}为单点集时,也可将S({w})简记为S(w).下一节将重点讨论S(w)的相关问题.在此之前,首先说明平坦半环的子半环与商半环的特点以及证明平坦半环上的同余恰为Ress同余.

命题 2.2设S为平坦半环,则有如下结论成立:

(1)S的任一子半环T均为平坦半环,其中子半环T按(2,2,0)型代数考虑,也即T需含有S中的零元;

(2)S的任一商半环S/ρ均为平坦半环;

(3)设A是S的任一非空子集,则

〈A〉={a1a2···an|ai∈S,i=1,···,n,n∈N}∪{0}.

其中〈A〉表示S中由子集A生成的子半环,也即S中包含A的最小子半环;

(4)设A是S的任一非空子集,则S1AS1是S中包含子集A的最小理想.

证明(1)设T为S的任一子半环.由引理2.1可知,只需验证(T,·)为0-可消半群即可.由于S中的零元在T中,从而亦是T的零元,因此结论显然成立.

(2)由引理2.1可知,只需验证(S/ρ,·)为0-可消半群即可.任取若,则有.由引理2.2可知,因此,ab=ac0.结合S的0-可消性可知,b=c,也即=.同理可知,由亦可推出=.故(S/ρ,·)为0-可消半群,结论得证.

(3)记等式右边的集合为B.若T是包含A的任一子半环,则有B⊆T.因此只需证明B是子半环即可.易知B≤(S,·).由0∈S结合 flat加法的性质可得,B≤(S,+).因此B是S的子半环,结论得证.

(4)类比(3)证明可知,结论显然成立.

引理 2.2设S为平坦半环.若ρ为(S,+)上的同余,则有

ρ=(0/ρ×0/ρ)∪1S=ρI,

其中I=0/ρ是 (S,+)上的理想.反之,若I是S是任一含 0的非空子集,则有I(S,+).

证明令ρ为(S,+)上的同余.任取a,b∈S且ab.若aρb,则有

a=a+aρa+b=0,b=b+bρa+b=0.

因此a,b∈0/ρ,即有ρ=(0/ρ×0/ρ)∪1S.再由命题 1.1可知,I=0/ρ是 (S,+)上的理想,进而ρ=ρI.

反之,若I是S是任一含0的非空子集,则有I+S=S+I=I.由定义可知,I(S,+).

上述引理表明(S,+)上的同余恰为Ress同余,而(S,+)上的理想也恰为S的某一含0的非空子集,且二者具有一一对应的关系.进而有如下命题:

命题 2.3设S为平坦半环,ρ⊆S×S.则ρ是S上的同余,当且仅当存在I(S,·),使得ρ=ρI.

证明充分性.若存在I(S,·),使得ρ=ρI,则ρI是 (S,·)上的同余.而I是含 0的非空子集,由引理 2.2可知,I(S,+).因此,ρI也是 (S,+)上的同余,进而ρ=ρI是S上的同余.

必要性.若ρ是S上的同余,则ρ是其加法导出(S,+)上的同余.故由引理2.2可知,ρ=(0/ρ×0/ρ)∪1S=ρ0/ρ.结合ρ亦是其乘法导出 (S,·)上的同余,由命题 1.1可知,0/ρ(S,·).这表明ρ=ρI,其中I0/ρ(S,·).

由上述命题可知,平坦半环上的同余均为Ress同余,且与乘法导出的理想具有一一对应的保序关系.进而有如下推论:

推论 2.1设S是非平凡的平坦半环.则S是次直不可约的,当且仅当(S,·)有唯一的0-极小理想.

定义 2.2设S是半环.若 (S,·)是 nil-半群,则称S为nil-半环.

定义 2.3[2]设S是平坦半环.若存在ω∈S{0},使得Sω=ωS={0},则称ω是S的零化子.

命题 2.4设S是非平凡的nil-平坦半环.则S是次直不可约的,当且仅当S有唯一的零化子ω.

证明必要性.由于S是次直不可约的,由推论2.1可知,(S,·)有唯一的0-极小理想I.而 (S,·)是 nil-半群,结合命题 1.2可知 |I|=2,不妨记为I={0,ω}.由理想的定义可知,任取s∈S,sω∈I.若sω=ω,则

ω=sω=s2ω=s3ω= ···,

而 (S,·)是 nil-半群,故ω=0,矛盾.因此,sω=0.同理可知ωs=0,从而ω是S的零化子.下证唯一性,设ω′是S的任一零化子.则{0,ω′}是 (S,·)的 0-极小理想.由 0-极小理想的唯一性可知,{0,ω′}={0,ω}.因此,ω′=ω.

充分性.若S有唯一的零化子ω,则I≜{0,ω}是 (S,·)的 0-极小理想.欲证S是次直不可约的,由推论 2.1可知,只需说明 (S,·)有唯一的 0-极小理想即可.设J为(S,·)的一个0-极小理想.由命题1.2可知,|J|=2.不妨设J={0,a}.由必要性证明可知,a是S的一个零化子.结合S有唯一的零化子可知,a=ω.因此,I=J.

若取W为自由半群X+的有限非空子集,则有S(W)是一个有限的nil-平坦半环,且W中的极大字恰为S(W)的零化子.因此,有如下推论:

推论 2.2设W为自由半群X+的有限非空子集.则下列命题等价:

(1)S(W)是次直不可约的;

(2)W中有唯一的极大字;

(3)存在w∈W,使得S(W)=S(w).

3 一类平坦半环生成的簇

从上一节可知,平坦半环是特殊的ai-半环,且关于子代数和商代数封闭.但平坦半环的直积未必是平坦半环,因此所有的平坦半环作成的类并不是一个簇,进而考虑由所有的平坦半环生成的簇,记作F.显然F是ai-半环簇AI的子簇.结合文献[4]可得下列两个引理:

引理 3.1F是由ai-半环簇AI填加下列恒等式所确定的簇:

a(x+y)b+c(x+y)d≈a(x+y)b+cxd.

其中,a,b,c,d中的任意一个均可为空.

引理3.2F中的次直不可约成员必为平坦半环.

接下来将主要讨论V(S(x1x2···xn))的有限基问题.首先,记Vn(n∈N)为F添加如下恒等式确定的簇:

其中,v∈{x1,x2,···,xk}+且vx1x2···xk;在 (5)式中,a,b中至少有一个为空;在(6)-(8)式中,a,b中任意一个均可为空.

显然S(x1x2···xn)满足上述恒等式,因此 V(S(x1x2···xn))⊆Vn,n∈N.下面将证明n=1,2,3时,V(S(x1x2···xn))=Vn.在此之前,先说明 Vn中次直不可约成员的一些基本性质:

引理 3.3设S是Vn中任一非平凡次直不可约成员.则有如下结论成立:

(1)S是平坦半环,它有唯一的零化子ω,进而{0,ω}是S的唯一0-极小理想;

(2)若存在k∈N,使得Sk={0}且Sk+1{0},则Sk={0,ω};

(3) 若存在b1,b2,···,bn,c1,c2,···,cn∈S, 使得b1b2···bn=c1c2···cn=ω,则有bi=ci,1≤i≤n;

(4) 若存在a1,a2,···,am∈S使得a1a2···am0,则

〈a1,a2,···,am〉=S(x1x2···xm),

其中〈a1,a2,···,am〉表示由{a1,a2,···,am}生成的子半环.

证明(1)由于S是Vn中的次直不可约成员,进而亦是F中的次直不可约成员.故由引理3.2可知,S是平坦半环.根据恒等式(2)可知,(S,·)是nil-半群,于是S是次直不可约nil-平坦半环.结合命题2.4可知,S有唯一的零化子ω.进而,{0,ω}是S的唯一0-极小理想.

(2)若存在k∈N,使得Sk{0}且Sk+1={0}.任取s=s1s2···sk∈Sk且s0.由于I是S的 0-极小理想,因而I⊆S1sS1.故存在u,v∈S1,使得ω=usv=us1s2···skv.结合Sk+1={0}可知,u=v=1,也即s=ω.这表明Sk={0,ω}.

(3)由恒等式(3)可知,结论显然成立.

(4)根据命题2.2(3)可知,只需证明:

〈a1,a2,···,am〉={aiai+1···aj|1≤i≤j≤m}∪{0}.

记等式右边的集合为A.显然A⊆〈a1,a2,···,am〉,所以只需说明〈a1,a2,···,am〉⊆A,且A中元素互不相同即可.任取v∈{a1,a2,···,am}+且va1a2···am.断言v=0,否则根据ω∈S1vS1可知,存在a,b∈S1使得ω=avb.进而a1a2···am+avb=0,这与恒等式 (6)矛盾,于是〈a1,a2,···,am〉=A.若A中有两个元素相同,不妨设aiai+1···aj=akak+1···aℓ,其中 1≤i≤j,k≤ℓ.下面分两种情形讨论:

(i)若j≤k,则利用恒等式(1)和恒等式(4)可知,任取a,b∈S,总有a2=aba=0.因此得到a1a2···am=0,矛盾.

(ii) 若j>k,记ai···ak=x,ak+1···aj=y,aj+1···aℓ=z,则有xy=yz0,于是xy+yz0,这与恒等式(2)矛盾.

综上所述,〈a1,a2,···,am〉=S(x1x2···xm).

由恒等式(1)得,Vn,V(S(x1x2···xn))均为局部有限簇.再结合

V(S(x1x2···xn))⊆Vn

可知,只需证 Vn中任一 (有限)非平凡次直不可约成员,均落在 V(S(x1x2···xn))即可.

定理3.1V(S(x1))=V1.

证明任取V1中的非平凡次直不可约成员S.由引理3.3(1)可知,S是次直不可约的平坦半环,且有唯一的0-极小理想{0,ω}.结合恒等式(1)可知,S2={0},从而(S,·)为 null-半群.因此S的任一含0非空子集均为S的理想.结合0-极小理想的唯一性可知,S={0,ω}S(x1)∈V(S(x1)).

定理3.2V(S(x1x2))=V2.

证明任取V2中的非平凡次直不可约成员S.由引理3.3(1)可知,S是次直不可约的平坦半环,且有唯一的0-极小理想{0,ω}.结合恒等式(1)可知,S3={0}.因此,分下列两种情形讨论:

(i)S2={0}.由定理 3.1可知,SS(x1)∈V(S(x1x2)).

(ii)S2{0}.由引理 3.3(2)可知,S2={0,ω}.于是存在x1,x2∈S,使得x1x2=ω0.由引理 3.3(4)可知,〈x1,x2〉=S(x1x2).断言S=S(x1x2),否则存在e∈SS(x1x2).结合ω∈S1eS1可知,存在a,b∈S1,使得ω=aeb.结合S3={0}且eω可知,a=1,b∈S或b=1,a∈S.再由引理3.3(3)可知,e=x1,b=x2或a=x1,e=x2,这与e∈SS(x1x2)矛盾.因此S=S(x1x2)∈V(S(x1x2)).

为了更好的刻画Vn,接下来引入“0-ω直并”的概念.进而说明V(S(x1x2···xn))中具有一类非常“典型”的次直不可约成员.

设 (Si)i∈I是一族次直不可约的 nil-平坦半环,且满足Si∩Sj={0,ω},i,j∈I且ij,其中,ω是Si(i∈I)的唯一零化子.令.任取a,b∈S,定义