Linearity of sendograph metric of fuzzy numbers

Fan Taihe,Li Yang

(Department of Mathematics Science,School of Science,Zhejiang Sci-Tech University,Hangzhou 310018,China)

Abstract：It is shown that the sendograph metric is not translation invariant.Basic properties of the sendograph metric under algebraic operations,as well as the continuity of the operations are discussed.It follows that with respect to the sendograph metric,the fuzzy number space can only be embedded into a topological vector space,but not into a normed linear space,as compared with the result about the supremum metric.Finally,a lower bound for the sendograph metric under translation is given.

Keywords：fuzzy number,sendograph metric,translation invariance

1 Introduction

Since the concept of fuzzy number was first introduced in the 1970′s,basic properties of various metrics and algebraic operations for fuzzy numbers have been investigated extensively[1-8].It should be noted that with respect to the supremum metric the fuzzy number space form a positive cone in a certain Banach space[9-10],this construction is very important since it enables the functional space method be used in the study of fuzzy number space.Since theLpmetrics are also defined via the distances between level cutsets,it is easy to observe that they have similar linear properties as the supremum metric.On the other hand,the sendograph metric is introduced in Reference[11]into the fuzzy number space as a natural 2-dimensional generalization of the Haudsorff metric by identifying fuzzy numbers with their sendographs and the sendograph metric was succcessfully used in fuzzy dynamic systems[12].Reference[1]is asserted without proof that the sendograph metric is translation invariant.In this paper we will show that in fact this is not the case in general and give a counterexample for the assertion.Moreover,we prove that the distance between two fuzzy numbers under sendograph metric may decrease after a translation.A lower bound for the distance after a translation,which is only related to the translation and the original distance,is given for the general case and the case when the translation is confined as a Lipschitzian fuzzy set,while in the latter case,the given lower bound is shown to be optimal.Finally,the homogeneity of the sendograph metric is investigated,and the continuity of the linear operations is also discussed.

For the basic notions used in this paper,please refer to Reference[1,13].

2 Preliminaries

Throughout this paper,ifAis a nonempty compact convex subset ofRn,∂Adenotes the boundary ofA.λdenotes the Lebesgue measure on the Borelσ-fieldB([0,1])of[0,1].

First,we recall the basics of the spaceEn.Each element ofEnis a fuzzy setu:Rn→I=[0,1]with the following properties:

(i)uis normal,i.e.,u(x0)=1 for somex0∈Rn;

(ii)uis quasiconvex(fuzzy convex),i.e.,u(rx+(1−r)y)≥min{u(x),u(y)}for allx,y∈Rnandr∈I;

(iii)uis upper semicontinuous(u.s.c.for short);

(iv)The topological support ofu:u0=cl{x|x∈R,u(x)>0}is compact.

The family of all such fuzzy sets is denoted byEn.In particular,the elements ofE1are called fuzzy numbers.

For eachu∈En,andα∈(0,1],letuαdenote theα-cut ofu,i.e.,

thenuαis a non-empty compact convex subset ofRn.

Foru∈En,let

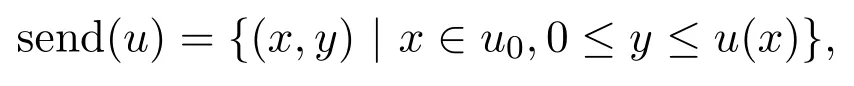
send(u)is called the sendograph ofu.Obviously,send(u)is a compact subset ofRn×I.Foru,v∈En,the sendograph metric[11]is define by

whereHis the Hausdorff metric between sets under consideration.For subsetsA,BofRn,define

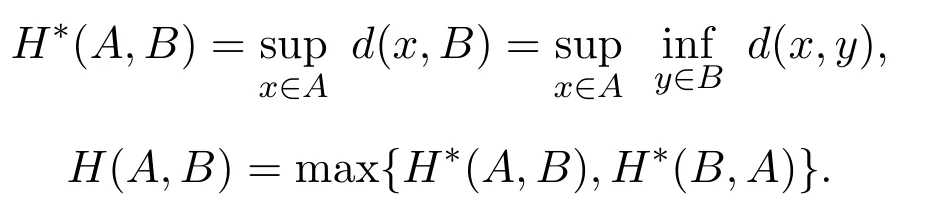
Wheredis the Euclidean metric.There are other three usual metrics on the fuzzy number space mentioned in this paper.The first one is the supremum metric defined by

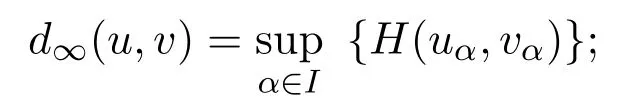
the second is theLpmetric defined by

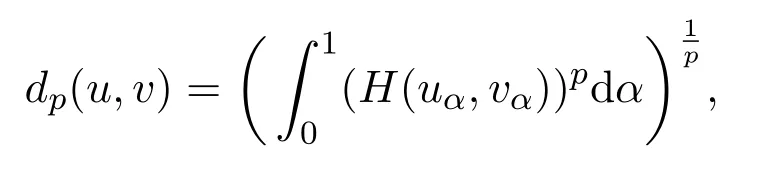
forp≥1;the third is the endograph metric defined by

where end(u)=send(u)∪Rn×{0}.The linear structure onEnis defined as follows:

For other basic notions about fuzzy metrics,please refer to Reference[1].

LetAbe a nonempty subset ofRn,the support function ofAis defined for allp∈Rnby

IfA,Bare nonempty compact convex subsets ofRn,then support function has following properties:

The concept of support function of a nonempty compact convex subset ofRncan be extended to the fuzzy sets ofEn.Letu∈Enand definesu:I×Sn-1→Rby

for(α,p)∈I×Sn-1.

One can easily observe that with respect to the supremum metric,the following properties hold:

and

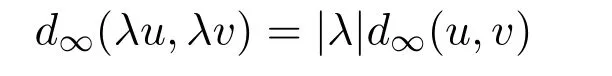
for any fuzzy numbersu,v,wand real numberλ.i.e.,the supremum metric is translation invariant and positively definite.The similar results are also true for theLpmetrics.In the following we will see that when dealing with the sendograph metric,things will become quite different.

3 Main results

Letu,v∈En,since send(u),send(v)are compact,there must be two elementsp∈send(u),q∈send(v),such thatd(p,q)=H(send(u),send(v)).By the following lemma,we can fix the locations ofpandqin send(u)and send(v)respectively.

Proposition 3.1For anyu,v∈En,let(y,β)∈{Rn×I}send(u),then there existsα∈I,x∈uα,such that

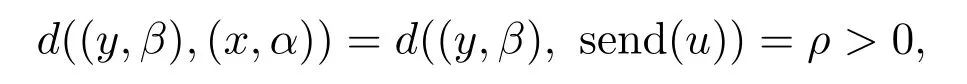
withα∈[β−ρ,β]∩[0,β].Additionally,ifβ−α<ρ,x∈∂uα;elsex=y.

IfH∗(send(v),send(u))=ρ>0,then there existsβ∈I,y∈∂vβ,such that

IfD(u,v)=H∗(send(v),send(u))=ρ,then there existsα,β∈I,x∈uα,y∈∂uβ,such thatd((x,α),(y,β))=D(u,v),withα∈[β−ρ,β]∩[0,β].Additionally,ifβ−α<ρ,x∈∂uα;elsex=y.

ProofIt is enough to note that the boundary of a fuzzy number is compact.Q.E.D.

Proposition 3.2For eachu,v,w∈En,we have

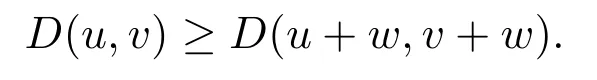
ProofSupposeH∗(send(v+w),send(u+w))=ρ>0.By proposition 3.1,there existsβ∈I,P∈vβ+wβ,such thatd((P,β),send(u+w))=ρwhich implies that there existsyv∈vβuβandyw∈wβsuch thatyv+yw=P.Again by proposition 3.1,there existsα∈[0,β]andxu∈uαsuch thatd((yv,β),(xu,α))=d((yv,β),send(u)).It follows fromxu+yw∈uα+wαthat

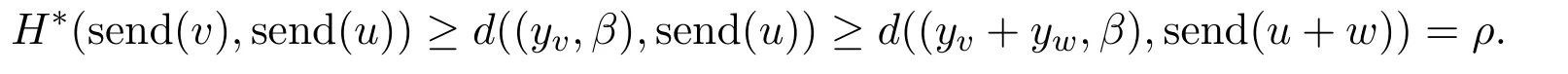
By duality,D(u,v)≥D(u+w,v+w).Q.E.D.

The Hausdorff metric on the family of compact convex subsets of finite dimensional Euclidean space is translation invariant,however,the sendograph metric,which is derived from the Hausdorff metric,does not have this property.The following is a counterexample.

Example 3.1Letu,v,w∈E1be defined as follows:

Remark 3.1By the above example,it follows that the sendograph metric is not translation invariant.On the other hand,it is easy to check that the supremum metric and theLpmetric are both translation invariant.This is mainly because that both the supremum metric and theLpmetric are determined by the Hausdorff metric of each level set only,while the Hausdorff metric on the space of all compact setsK(Rn)inRn,is translation invariant.Although the sendograph metric does not have this property,the following proposition 3.3 shows the equivalence of convergence of sequence of fuzzy numbers under translation.

Lemma 3.1[7]Suppose that(um)m∈Nis a sequence of elements inEn.Then(um)m∈Nconverges tou∈Enwith respect toDif and only if

(S2)there exists a Borel set Λ∈B[0,1]withλ(Λ)=1 such that for everyα∈Λ the equality

Proposition 3.3Forum,u,w∈En,we haveif and only if

ProofNecessity:By lemma 3.1,if,then(un)0→u0and there exists a dense subsetS⊆I,such that(un)α→uαfor eachα∈S.So we have(un+w)0→(u+w)0and(un+w)α→(u+w)αfor eachα∈S.Again,by lemma 3.1,it follows that

Sufficiency:the proof of the necessity part is reversible.Q.E.D.

In the following we investigate under translation how the sendograph metric depends on the fuzzy sets under consideration.If the translation fuzzy setwis a crisp interval,then obviously we haveD(u,v)=D(u+w,v+w).By discussing the general case ofE1,the following proposition reveals the quantitative relationship betweenD(u,v)andD(u+w,v+w)with respect to the upper bound ofH(w0,w1).

Proposition 3.4Foru,v,w∈E1,ifρ=D(u,v)>0 andH(w0,w1)∈Am,then

(2)Obviously,D(λnun,λu)≤D(λnun,λnu)+D(λnu,λu).

Since|λn−λ|→0,then{λn}is bounded.Suppose|λn|≤cfor somec≥1.By proposition 3.5,D(λnun,λnu)≤cD(un,u).

Since the scalar multiplication is continuous under the Hausdorff metric onK(Rn+1),thus,forα∈[0,1],we haveH(λnuα,λuα)→0.By lemma 3.3 and lemma 3.4,it follows thatD(λnu,λu)→0.Therefore,we can conclude thatD(λnun,λu)→0.Q.E.D.

Remark 3.3Consider the embedding of the fuzzy number space into Banach space introduced in Reference[9].

Example 3.1 shows that this can not be true for the sendograph metric.However,from proposition 3.6 and the fact that the sendograph metric can be easily extended into¯C[0,1]to form a topological vector space(for basic notions about topological vector space,please refer to Reference[13],it follows thatE1can be embedded into a topological vector space with respect to the sendograph metric as a positive cone.This makes it is possible that the method of topological vector space be used in the study of fuzzy number space with the sendograph metric.We think that it might be an interesting question to study this embedding.

4 Conclusions

Although the fuzzy number space does not form a positive cone with respect to the sendograph metric as the supremum metric and theLpmetrics do.However,it might be embedded into a topological vector space.We think that the results of this paper may be a remedy for this deficiency of the sendograph metric.The behaviors of the sendograph metric with respect to linear operations are fully cleared out.The result in this paper might be used to the study of fuzzy number space via sendograph metric like the linearity of fuzzy number space with respect to other metrics and applications of fuzzy metrics in problems such approximations of fuzzy numbers(see References[14-16]).This would be our interest of future study.