非负矩阵分解与非负张量分解:算法与应用
宋 珊,冯 岩,徐常青
(苏州科技大学 数学科学学院,江苏 苏州 215009)
科学研究和实际问题中的大量观测数据,如距离、体积、压强、降雨量、溶液浓度和网络可靠性等度量数据都具有非负性,这些数据集合经适当处理后可表示为非负阵列(包括标量和向量)形式,如信息论中的熵(entropy),索引图像或视频流,物理中的矩、速度场和量子场,概率统计学中的概率,网络中的连通度等[1-2]。这些带非负特征的数、向量或矩阵甚至高阶张量的每个元素因其非负性而具有可解释性(物理意义)。但是,人们所熟知的矩阵分解,如矩阵满秩分解、奇异值分解(SVD)和QR分解等,得到的因子矩阵一般不具备非负性,这一方面限制了其物理应用(分解得到的因子矩阵不可解释),另一方面也会增大计算误差和分解难度。
非负矩阵分解(Nonnegative Matrix Factorization,简称NMF)产生于1994年,最早由Paatero和Tapper[3]在研究元素非负的正定矩阵分解时提出。1999年,Lee和Seung[4-5]将NMF方法运用于人脸识别技术,并于2000年提出乘性迭代算法。随后,在乘性迭代算法的基础上产生了很多推广的NMF高效算法,如Cichocki等人[6-7]在2006年提出NMF的推广智能化算法,并在2007年提出层次交替最小二乘算法,而Lin[8]在2007年提出NMF的投影梯度算法。
非负张量分解(Nonnegative Tensor Factorization,简称NTF)最早在2005年由Shashua和Hazan[9]提出,他们是在研究如何提取图片局部特征时建立了三阶非负张量分解模型,并用非负梯度下降法求解该模型。2009年,Zafeiriou[10]提出基于KL散度和广义Bregman距离的NTF算法,并给出收敛性证明。2011年,刘昶等人[11]提出张量的正交非负CP分解算法并用于图像表示和识别。2016年,梁秋霞等人[12]提出基于NTF的人脸识别算法。实际情况下,对规模较大、阶数高(例如10阶以上)的非负张量分解,目前并没有可行的分解算法。2014年,祁力群、徐常青和徐毅通过定义张量的分层对角占优给出了一类对称非负张量的非负分解,并给出了较好的算法[13]。
1 NMF模型及算法
给定观测值矩阵Y∈R+n×m,其中R+n×m表示由所有元素非负的n×m的矩阵构成的集合。Y对应的非负矩阵分解(NMF)Y≈AX等价于非负线性约束下的线性模型

1.1 代价函数
为了求解因子矩阵A和X,首先需要衡量AX对Y的逼近程度,即误差矩阵E的大小。Lee和Seung在文献[5]中选取欧氏距离和KL散度构造了两种代价函数。
基于欧式距离的代价函数为

此时因子矩阵求解问题转化为最优化问题

基于KL散度的代价函数为

此时模型问题(1)转化为最优化问题
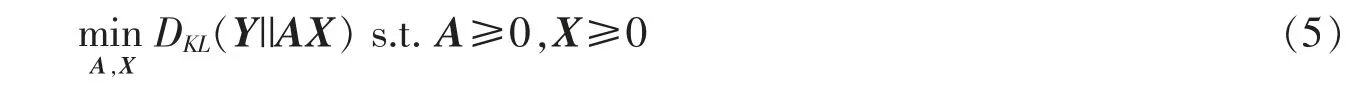
1.2 迭代算法
针对最优化问题(3)和(5),常用的迭代算法有:乘性迭代算法(MU)和交替最小二乘算法(ALS)。
1.2.1 乘性迭代算法
Lee和Seung提出的乘性迭代算法是在梯度下降法基础上赋予了特定步长得到的。该迭代算法具有收敛速度较快和可操作性强等优点,且只要保证A和X的初值非负,那么每一次迭代得到的结果都是非负的。文中以最优化问题(3)为例,具体说明基于欧氏距离的乘性迭代算法的求解过程。
设A ik和X kj的梯度下降算法迭代规则为

其中
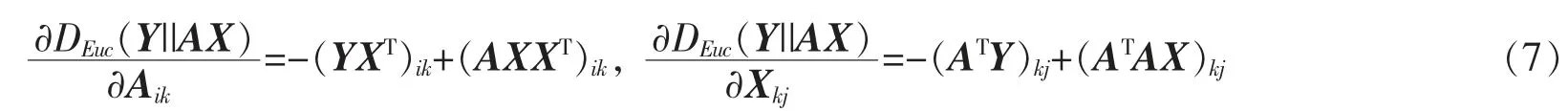
将(7)式代入(6)式,得

(9)式即为基于欧氏距离的乘性迭代规则(简称MUEuc)。在下面的算法中,运用矩阵形式来表述该算法的迭代规则。先给出算法中相关符号的说明:*表示两个大小相同的矩阵按元素对应相乘,/表示两个大小相同的矩阵按元素对应相除。
算法1 NMF-MUEuc算法
输入:Y,r,ε,maxiter;
输出:A,X;
步骤1:随机初始化矩阵A,X,确保非负,初始化计数器k=0;
步骤2:计数器自增k=k+1,并求解(2)式的值DEuc(Y||AX),若DEuc(Y||AX)<ε或k>maxiter,则进入步骤4,否
则进入步骤3;
步骤3:A和X按(9)式的矩阵形式进行迭代

迭代后进入步骤2;
步骤4:迭代结束,返回A,X。
同理,可以得到基于KL散度的乘性迭代规则(简称MUKL)

并用矩阵形式写成算法。
算法2 NMF-MUKL算法
输入:Y,r,ε,maxiter;
输出:A,X;
步骤1:随机初始化矩阵A,X,确保非负,初始化计数器k=0;
步骤2:计数器自增k=k+1,并求解(4)式的值DKL(Y||AX),若DKL(Y||AX)<ε或k>maxiter,则进入步骤4,否则
进入步骤3;
步骤3:A和X按(11)式的矩阵形式进行迭代

这里1表示n×m的全1矩阵。迭代后进入步骤2;
步骤4:迭代结束,返回A,X。
1.2.2 交替最小二乘算法
交替最小二乘算法(Alternative Least Square,缩写为ALS)主要用于求解最优化问题(3)。它的基本思想是:先固定A并通过最小化目标函数(2)求非负因子矩阵X,再代入计算得到的X,并通过最小化目标函数(2)进一步更新非负因子矩阵A,循环往复,直至代价函数(2)产生的两个矩阵序列收敛为止。根据最小二乘法,易知当A固定时等价于矩阵方程ATAX=ATY在已知A,Y的情形下估计X。同样固定X时等价于矩阵方程XXTAT=XYT在已知X,Y的情形下估计A。如此便可求得交替最小二乘算法的迭代公式

下面将上述流程写成具体算法:
算法3 NMF-ALS算法
输入:Y,r,ε,maxiter;
输出:A,X;
步骤1:随机初始化矩阵A,X,确保非负,初始化计数器k=0;
步骤2:计数器自增k=k+1,并求解(2)式的值DEuc(Y||AX),若DEuc(Y||AX)<ε或k>maxiter,则进入步骤4,否
则进入步骤3;
步骤3:X和A按(13)式进行迭代,迭代后进入步骤2;
步骤4:迭代结束,返回A,X。
1.3 算法比较
下面通过数值实验比较基于欧氏距离的乘性迭代算法(算法1)和交替最小二乘算法(算法3)的优劣。随机生成一个500×100的矩阵,元素介于0~1之间,取特征维数r=5,用算法1和算法3对生成矩阵进行分解,画出代价函数(2)在不同迭代次数和运行时间下的示意图(图1(a)和图1(b))。从图中可以看出,最开始的时候(Epoch<10,Time<0.01),在相同的迭代次数和运行时间下,NMF-MUEuc算法得到的代价函数值比NMF-ALS算法小,随着迭代次数和运行时间的增长,NMF-MUEuc算法得到的代价函数值又比NMF-ALS算法大,最后两者的代价函数值趋于一致。这说明NMF-MUEuc算法开始的时候收敛速度比NMF-ALS算法快,之后比NMF-ALS算法慢,但两者最终都收敛到大致相同的平稳点。

图1 不同迭代次数和运行时间下代价函数的变化
2 NTF模型及算法
NMF模型(1)可推广到非负张量分解(NTF)模型,该文着重于三阶非负张量的分解。给定找到非负因子矩阵使得

2.1 代价函数
与NMF情形相类似,为了求解因子矩阵U,V,W,需要先衡量[U,V,W]对X的逼近程度,即E的大小。Shashua和Hazan在文献[9]中同样选取欧氏距离和KL散度构造了两种代价函数。基于欧式距离的代价函数为
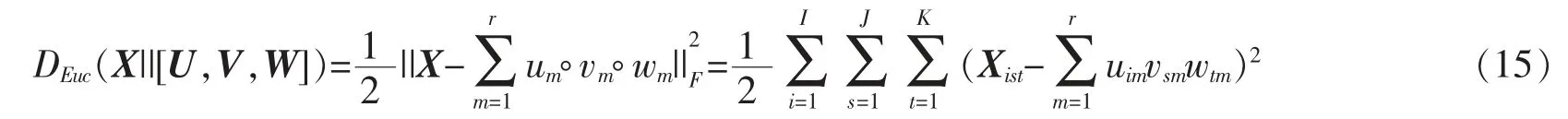
此时因子矩阵求解问题转化为最优化问题

基于KL散度的代价函数为

此时因子矩阵求解问题转化为最优化问题
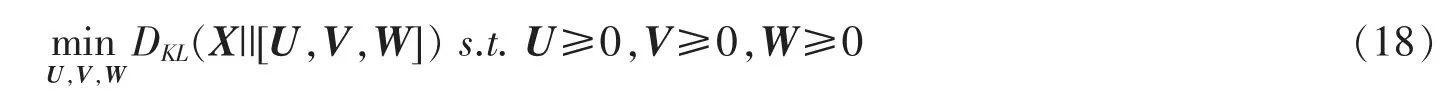
2.2 迭代算法
针对最优化问题(16)和(18),文中介绍最常用的乘性迭代算法,它是其他所有推广算法的基础。与NMF的乘性迭代算法类似,NTF的乘性迭代算法同样是在梯度下降法的基础上赋予了特定步长得到的。下面以最优化问题(16)为例,具体说明基于欧氏距离的乘性迭代算法的求解过程。
设uij的梯度下降迭代规则为

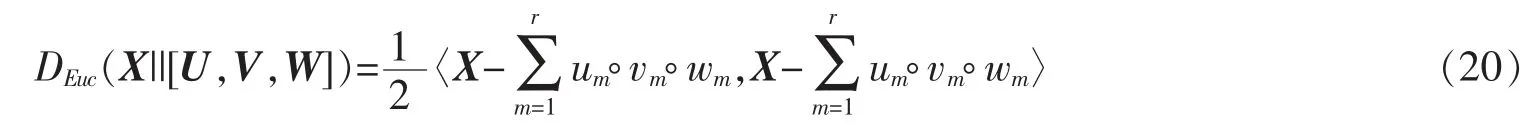

所以

其中e i表示I阶单位矩阵的第i个列向量。将(21)式代入(19)式得

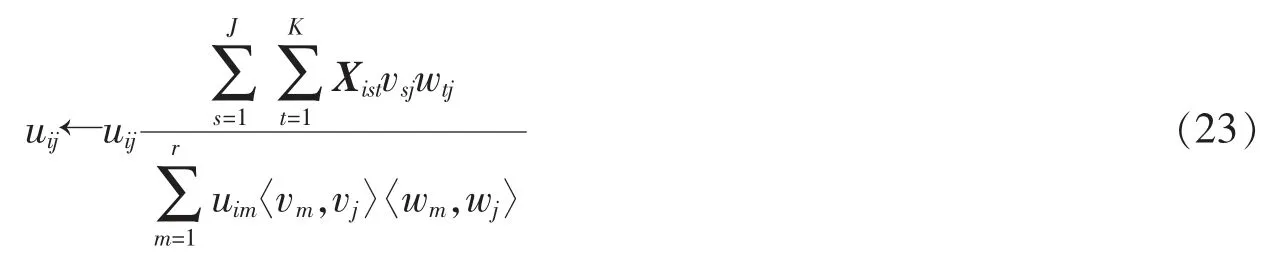
同理,可得vsj和wtj的乘性迭代公式

(23)、(24)和(25)构成NTF的基于欧式距离的乘性迭代规则。在此规则下,只要U,V,W的初值非负,那么每次迭代得到的结果都是非负的。Shashua和Hazan在文献[9]中给出了算法的收敛性证明。在下面的算法中,将上述迭代规则运用矩阵的Khatri-Rao积和张量的矩阵化进行改写。矩阵A=[a1,a2,…,an]∈Rm×n和B=[b1,b2,…,bn]∈Rp×n的Khatri-Rao积为

其中⊗为Kronecker乘积,A⊗B表示A的每个元素乘以B。三阶张量沿模-1,模-2,模-3方向的矩阵化结果记为X(1),X(2),X(3),其中X的元素xi1i2i3与矩阵X(k),k=1,2,3的元素xik j是一一对应的,并且有

算法4 NTF-MUEuc算法
输入:X,r,ε,maxiter;
输出:U,V,W;
步骤1:随机初始化矩阵U,V,W,确保非负,初始化计数器k=0;
步骤2:计数器自增k=k+1,计算(15)式的值DEuc(X||[U,V,W]),若DEuc(X||[U,V,W])<ε或k>maxiter,则进入
步骤4,否则进入步骤3;
步骤3:U,V,W按(23)、(24)、(25)式的矩阵形式进行迭代

其中A=W⊙V,B=W⊙U,C=V⊙U。迭代后进入步骤2;
步骤4:迭代结束,返回U,V,W。
同样,可以得到NTF的基于KL散度的乘性迭代规则

该乘性迭代规则的收敛性由Zafeiriou在文献[10]中用构造辅助函数的思想证明。下面将迭代规则用矩阵形
式写成算法。
算法5 NTF-MUKL算法
输入:X,r,ε,maxiter;
输出:U,V,W;
步骤1:随机初始化矩阵U,V,W,确保非负,初始化计数器k=0;
步骤2:计数器自增k=k+1,计算(17)式的值DKL(X||[U,V,W]),若DKL(X||[U,V,W])<ε或k>maxiter,则进入
步骤4,否则进入步骤3;
步骤3:U,V,W按(29)、(30)、(31)式的矩阵形式进行迭代


迭代后进入步骤2;
步骤4:迭代结束,返回U,V,W。
3 实验模拟
下面将非负矩阵分解和非负张量分解的基于欧式距离的乘性迭代算法(算法1和算法4)用于人脸识别的特征提取,通过识别准确率比较它们之间的优劣。
3.1 实验条件和参数设定
文中实验环境为PC机,CPU2.10 GHz,Windows10,Matlab(2014a)。实验数据来自AR数据库和ORL数据库,从AR数据库中下载100个人的像素为165×120的面部灰度图像,共2 600张,其中每个人有26种不同的姿态(可看成一类)。从ORL数据库中下载40个人的像素为112×92的面部灰度图像,共400张,其中每个人有10种不同的姿态(可看成一类)。在实验开始前,为了使实验数据满足文中算法的要求,对面部灰度图像进行预处理。首先,把面部图像裁剪成60×60像素的图像,再把灰度值介于0~255之间的uint8类型的数据转换为灰度值介于0~1之间的双精度(2double)数据。实验过程中所有的实验参数都视情况而定。
3.2 实验步骤
对AR数据库作两组实验:实验一是从每类中随机选取5张图像作为训练样本,其余为测试样本;实验二是从每类中随机选取10张图像作为训练样本,其余为测试样本。对ORL数据库也作两组实验:实验一是从每类中随机选取4张图像作为训练样本,其余为测试样本;实验二是从每类中随机选取6张图像作为训练样本,其余为测试样本。最后通过最近邻分类器实现人脸识别。
3.3 结果分析
表1和表2分别是AR数据库和ORL数据库的识别率比较表。从表中可以看出,不管是AR数据库还是ORL数据库,随着特征维数和训练样本数的增加,NMF-MUEuc算法和NTF-MUEuc算法的识别率都在逐步提高,但当特征维数和训练样本数相同时,NTF-MUEuc算法的识别率总比NMF-MUEuc算法的识别率高,说明NTF-MUEuc算法对人脸特征提取的更好。

表1 AR数据库识别率比较表

表2 ORL数据库识别率比较表
4 结语
首先,介绍NMF模型在不同代价函数下的乘性迭代算法和交替最小二乘算法,并通过实验比较两种算法的不同;其次,介绍NTF模型在不同代价函数下的乘性迭代算法;最后,用具体的人脸识别实验说明NTF算法比NMF算法在人脸特征提取上更有优势。

