Properties and criterions of spherically convex functions
ZHANG Yin,GUO Qi
(School of Mathematical Sciences,SUST,Suzhou 215009,China)
Abstract:In this paper,we studiedthe properties and criterions of spherically convex functions.The continuity of spherically convex functions was confirmed,and two criterions were established,which are the spherical analogues of those for convex functions.The results obtained here enrich the theory on spherically convex functions and contribute to the further study.
Key words:spherically convex set;spherically convex function;criterion of convexity
1 Introduction
The spherical convexity theory,including the study on spherically convex sets,spherically convex functions and their applications,emerged a century ago(see[1-3]and the references therein),however,opposite to the situation in Euclidean convexity,it developed very slowly for a quite long time due to the lack of basic compositions and transformations on spheres.Luckily,the study on spherical convexity starts getting more and more attentions in the last two decades,in particular,the study on spherically convex sets(see[4-10]and the references therein).However,the first clear definition of spherically convex function appeared just last decade([11]),and then another definition was proposed very recently([7,12]).As far as we know,these two definitions are the only ones available in the literature.
These two definitions are with completely different appearances.Ferreiraet alpresented several criterions for the spherically convex functions defined in[11],which are convenient and useful tools in checking the convexity of functions and in applications.What we would like to point out is that similar criterions for the spherically convex functions defined in[7,12]are not easy to establish.Alike,from the definition given in[7,12],one may derive some spherical analogues of conclusions for Euclidean convex functions,such as the Jensen’s inequality etc,which are hard to obtain from the spherical convexity defined in[11].
As well known,the criterions for convexities of functions and the generic properties,such as the Jensen inequality of functions etc,are important topics in convex analysis.As mentioned above,the two definitions have their own advantages in different topics.So,to make full use of the advantages of spherically convex functions,we need investigate the relations of these two definitions.Notice that it was mentioned but without proof in[7]that these two definitions are actually equivalent.Thus,in this short article,we will discuss in details some properties,in particular the criterions,of the spherically convex functions,which might play roles in providing a precise argument for the equivalence of these two definitions.
2 Preliminaries
Rn,Sn-1denote the Euclideann-space and its unit sphere,respectively.〈·,·〉and||·||denote the usual inner product and the norm induced by||·||on Rn,respectively.The slightly modified radial mapρ:Rn→Sn-1∪{o}is defined byρ(x):=x/||x||forx≠oandρ(o)=o.With the help of the radial map,a spherical addition“+s”on Rnis defined asx+sy:=ρ(x+y),x,y∈Rn,and spherically convex combinations are defined as well byWe writeλx+s(1-λ)ysimply instead of(s)(λx+(1-λ)y).
Foru∈Sn-1andr∈R,we denote the hyperplaneHu,r:={x∈Rn|〈u,x〉=r},the open half space〈u,x〉>r}and the closed half spacerespectively;By replacing“>”,“≥”with“<”,“≤”respectively,we denotein a similar way.In particular,we write simplyinstead ofHu,0,respectively.We refer to[13-14]for other notation and terms.
According to the definition of analytic form given in[7,15](equivalent to the popular one used in[5-6,11]),a nonempty setC⊂Sn-1is called spherically convex(s-convex for brevity)ifλu+s(1-λ)v∈Cwheneveru,v∈C,λ∈[0,1]withλu+s(1-λ)v≠o(equivalentlyλu+(1-λ)v≠o).If furtherCcontains no antipodes,it is called a propers-convex set.Two pointsu,v∈Sn-1are called(a pair of)antipodes ifv=-u.Clearly,u,v∈Sn-1are antipodes if and only if 1/2u+s1/2v=o,and ifu,v∈Sn-1are not antipodal,thenλu+s(1-λ)v≠ofor allλ∈[0,1].For a nonemptyS⊂Sn-1,the set

is called the spherically convex hull(s-convex hull for brevity)ofS,which is ans-convex set.
Foru,v∈Sn-1,the intrinsic distanceds(u,v)between them is defined asds(u,v):=arccos〈u,v〉,i.e.the angle between vectorsu,v([8]).Clearly 0≤ds(u,v)≤π,ds(u,v)=0 if and only ifu=vandds(u,v)=πif and only ifu=-v.It is easy to see that the intrinsic distance is equivalent to the Euclidean one on Sn-1,so the limitu→u0or limu=u0can be understood as eitherds(u,u0)→0 or||u-u0||→0.
A set of the formV∩Sn-1,whereV⊂Rnis a 2-dimensional subspace,is called a great-circle.A set of the formis called an open(resp.closed)hemispheredefined in a similar way).The following conclusion was proved in[7,12].
Proposition 1[7,12]is ans-convex set,thenCis contained in a closed hemisphere;is a proper closeds-convex set,thenCis contained in an open hemisphere.
A continuously differentiable functionγ:[a,b]→Sn-1,where[a,b]⊂R is a closed interval,is called a geodesic segment(function)ifγ([a,b])is contained in some great-circle.The numberis defined as the length ofγ.A geodesic segment is called minimal iffor anya≤a1≤b1≤b.If further||γ′(t)||≡1,thenγis called a normalized minimal geodesic segment(see[11]for more details).It is known that for any distinctu,v∈Sn-1,there is a unique normalized minimal geodesic segment

whereα:=ds(u,v).
In the following,we recall the definitions of spherically convex functions and their known properties.
LetC⊂Sn-1be ans-convex set andf:C→R be a function.fis calleds*-convex if for any minimal geodesic segmentγ:[a,b]→C,the functionf◦γ:[a,b]→R is convex(cf.[11]);fis calleds-convex iff(λu+s(1-λ)v)≤λf(u)+(1-λ)f(v)wheneveru,v∈Candλ∈[0,1]withλu+(1-λ)v≠o(cf.[7,12]).
The properties ofs*-convex functions are discussed in details,and several useful criterions ofs*-convex functions are established in[11],which,however,are hard to establish fors-convex functions.Similarly,[7,12]proved several conclusions fors-convex functions,which,however,are hard to establish fors*-convex functions.Here we collect some conclusions fors-convex functions from[7,12]for the later use.
Theorem 1(Jensen’s Inequality) LetC⊂Sn-1be ans-convex set andf:C→R be ans-convex function.Then,

whenevervi∈C,λi∈[0,1],1≤i≤mwith
Theorem 2LetC⊂Sn-1be ans-convex set andf:C→R be ans-convex function.Then,there areu0∈int(coC),(v*,b)∈Rn×R,such that

From the discussion above,we see that proving the equivalence of these two definitions becomes a valuable topic.So,in Section 3 and 4 we will discuss the properties,in particular,the criterions,ofs-convex functions in the hope to find some clues for dealing with such a topic.
3 Some properties of s-convex functions
In this section,we study further the properties ofs-convex functions,starting with the discussion on the continuity ofs-convex functions.Given a function defined in a setS⊂Sn-1and a pointu0∈E,we say thatfis rela-tively continuous atu0ifholds.Iffis relatively continuous at each point ofS,we say that it is relatively continuous inS.
Theorem 3LetC⊂Sn-1be ans-convex set andf:C→R be ans-convex function.Thenfis relatively continuous in riC.
To prove Theorem 3,we need some more preparations.First,foru,v∈Sn-1withv≠±u,we denote

Then,we have the following elementary but useful equality revealing the relation betweenγ*uvandγuv.
Proposition 2Letu,v∈Sn-1withv≠±u.Thenγ*uv(θ)=γuv(t)if and only if
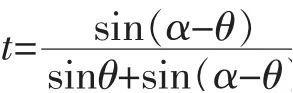
Proof.Clearlyγ*uv(θ)=γuv(t)if and only ifds(u,γuv(t))=ds(u,γ*uv(θ))(=θ).For brevity,denote
By an elementary geometric calculation,we see thatds(u,γuv(t))=θif and only if(noticing||u-v||=2sin),
and in turn

Lemma 1LetC⊂Sn-1be ans-convex set with intC≠Øandf:C→R be ans-convex function.Then,for eachu∈intC,there areδu>0,Mu,mu∈R such that

Proof.IfC=Sn-1,thenfis a constant(cf.[7]),and so the conclusion is trivial.Thus,we assumeC≠Sn-1.Letu∈intC.It is easy to see that there are affinely independentv1,v2,…,vn∈Csuch thatu∈int(cos{vi|1≤i≤n}),Denotingwe have by Theorem 1,forw=(s)cos{vi|1≤i≤n},

On the other hand,by Theorem 2,there areu0∈int(coC),(v*,b)∈Rn×R,such thatf(w)≥〈v*,w-u0〉+bfor allw∈C.Since cos{vi|1≤i≤n}is compact and〈v*,·-u0〉+bis continuous,mu:=min{〈v*,w-u0〉+b|w∈cos{vi|1≤i≤n}}exists.Thus,for

Now,choosingδu>0 such that,we complete the proof.
Lemma 2LetC⊂Sn-1be ans-convex set with intC≠Øandf:C→R be ans-convex function.Suppose there areu0,δ,mandMsuch that

Then

whereLM,m,δ:=(M-m)/sinδ,i.e.fis Lipschitz-continuous onIn particular,fis continuous atu0.
Proof.Similarly,we need only to argue for the caseC≠Sn-1(which impliesδ≤π/4 sinceCis now contained in a closed hemisphere by Proposition 1),and we assumeu≠vfor otherwise there is nothing to prove.
By Proposition 2,u=λw+s(1-λ)vwhere.Thus,by thes-convexity off,

which leads to

whereLM,m,δ:=(M-m)/sinδ.Exchanging the roles ofu,v,we havef(v)-f(u)≤LM,m,δds(u,v)as well.Hence

The proof is completed.
Proof of Theorem 3Clearly,only the sphere generated byC(i.e.the smallest sphere containingC)is relevant,so we may consider only the case intC≠Ø.Thus,the conclusion follows from Lemma 1 and Lemma 2. □
Now,we discuss some other properties ofs-convex functions.LetC⊂Sn-1be ans-convex set andf:C→R be a function.Then,the sub-level setSr(f)offwith levelris defined as

The following is a spherical analogue of the conclusion for sub-level sets of an Euclidean convex function.
Proposition 3LetC⊂Sn-1be ans-convex set andf:C→R be ans-convex function.Then,each nonempty sub-level setSr(f)is ans-convex set.Moreover,if nonemptySr(f)⊂riC,thenSr(f)is a closeds-convex set.
Proof.IfSr(f)≠Ø,then for anyu,v∈Sr(f)andλ∈[0,1]withλu+(1-λ)v≠o,we have clearly by the definition ofs-convex functions,

So,λu+s(1-λ)v∈Sr(f)wheneverλu+(1-λ)v≠o.
The closedness ofSr(f)contained in riCfollows from the continuity offon riCconfirmed by Theorem 3. □
Remark 1It is easy to find an example to show that the converse of Proposition 3 is not true in general.
Next theorem shows that,similar to the conclusion for convex functions,a local minimum of ans-convex function is its global minimum.
Theorem 4LetC⊂Sn-1be ans-convex set andf:C→R be ans-convex function.If there areu0∈riCand δ>0 such that

then,f(u0)≤f(u),∀u∈C.
Proof.Suppose there isu1∈Cwithf(u1)<f(u0).Then,for allλ∈[0,1],we have

Now,choosingλ′∈(0,1)such thatλ′u0+s(1-λ′)u1∈Bs(u0,δ)∩C,we obtain

a contradiction.The proof is completed.
4 Criterions of spherically convex functions
In this section,we present some criterions ofs-convex functions,which are analogues of those of Euclidean convex functions.
The first one may be viewed as the spherical analogue of the criterion of increasing slopes for convex functions.
Theorem 5LetC⊂Sn-1be a propers-convex set andf:C→R ba a function.Thenfiss-convex if and only if,for any distinctu1,u2,u3∈Cwithu2∈(u1,u3)s,

Proof.Suppose thatfiss-convex and distinctu1,u2,u3∈Cwithu2∈(u1,u3)s.Thenu2=λu1+s(1-λ)u3for someλ∈(0,1).By Proposition 2

Thus,by thes-convexity off,

which leads to

Hence,after simplifying,we have

Conversely,suppose that(3)holds for any distinctu1,u2,u3∈Cwithu2∈(u1,u3)s.Then we see(2)directly from(3)and in turn(1)from(2).Applying(1)to anyu,uλ,v∈C,whereuλ:=λu+s(1-λ)v,we have by Proposition 2 again,

So,fiss-convex onC.
The following criterion can be proved by a similar argument.
Theorem 6LetC⊂Sn-1be a propers-convex set andf:C→R ba an function.Thenfiss-convex if and only if,for any distinctu1,u2,u3∈Cwithu2∈(u1,u3)s,

Final RemarkThis article concerns with the properties of the so-calleds-convex functions defined in[7,12].It is already seen that some conclusions,e.g.,Theorem 3,Proposition 3 and Theorem 4,obtained here are hard to establish for thes*-convex functions defined in[11].Hence,it is indeed valuable to confirm the equivalence ofs-convexity ands*-convexity of a function.Here,as main contributions,Theorem 5 and Theorem 6 give rise to a hope to prove such an equivalence:if one can show that Theorem 5 or Theorem 6 still holds fors*-convex functions,then thes-convexity ands*-convexity are equivalent.We will continue to work on this topic in the future.

