巧用转化,玩转数学
张彩萍





【摘 要】转化思想是数学核心思想之一,它在苏教版教材中有所体现,也是解决问题的主要策略之一。不难发现,在日常教学中,很多教师对此思想的应用完全不够,致使部分内容的教学效果大打折扣。因此,在教学中,教师应巧用转化思想,善于引导,将转化思想应用于数学教学之中。
【关键词】转化思想;小学数学;数学教学;苏教版
苏教版小学数学教材将转化作为解决问题的策略单独教学并着重强调。熟知教材便不难发现,转化思想并不存在于一个课时或一节数学课中,它已然贯穿整个小学数学教材,深入几乎每一课中。因此,了解转化思想的应用,并将之渗透于日常教学尤为重要。
一、知其用途,理解转化
(一)由繁入简,优化策略
在解决一些小学数学问题时不难发现,对于一些复杂问题,如果直接去处理、解决,难以找到着手点。此时可借助转化的思想方法,分析问题后,将复杂的问题简化,以寻找新的简单的生长点和着力点。
转化思想在苏教版教材中的体现:在苏教版小学数学四年级下册的学习中,将复杂的综合算式通过运算律简化,转化成便于计算的简单算式;在六年级上册,在计算不规则物体体积时,将物体放入有刻度的水量杯中,将物体体积转化为可测的水的体积,将问题简化等。
不规则图形面积的求解是苏教版五年级下册学习的一个重难点,因为图形的不规则性,所以学生很难或无法直接求解。
如苏教版五年级下册《解决问题策略——转化》中的例1:下面两个图形,哪个面积大一些?
学生以前比较面积大小的方式一般为观察法、重叠法,最准确的就是计算法。显然,在这个问题中,观察法和重叠法都无法使用,所以要用计算法。但是计算不规则图形面积,直接计算,于五年级生而言比较困难,计算烦琐,学生有些犯难。
因此,教师可引导学生将复杂的不规则图形转化为简单的常见几何图形:
通过转化,可将上图中不规则的图形转化为规则的长方形。
1.可以直接看出两幅图面积相等。
2.可以利用长方形面积公式——S=ab,直接求解。
通过转化,能将复杂的、难以直接解决的问题转化为简单的问题,轻松解决,优化解决问题的方法。
(二)以旧衍新,迁移新知
以旧衍新,即通过转化,将以前未接触未学习过的新知识转化学生已经接触并掌握的知识进行学习,将遇到的新问题转化成学生已经熟悉的问题去解决。通过原有知识和新知识之间的联系,实现转化,使知识获取更简单。
在小学数学教学中,通过转化以旧衍新,无处不在。在计算中,将小数的计算转化为学生熟悉的整数计算,迁移计算方法;将异分母分数转化成同分母的分数进行相加减,这样能极大地降低计算难度;将分数的除法转化为分数的乘法进行计算;在几何图形的计算中,将平行四边形通过剪切、平移等方式,转化成和它面积相同的长方形进行计算;将三角形和梯形的面积通过拼接等方式,转化成平行四边形进行计算等。如苏教版五年级上册《平行四边形的面积》一课中的例1:你能将下面平行四边形转化成长方形吗?
教材出题者没有让学生直接计算平行四边形的面积,而是将之先转化为学生已知的长方形,再进行下一步研究。学生得出两种转化的方式(如下图):
紧接着,教材出示“将书本115页的长方体剪下来,剪一剪,拼成长方体填表”。通过教师的引导,学生能够得出:
1.平行四边形的底通过转化成为长方形的长。
2.平行四边形的高通过转化成为长方形的宽。
3.平行四边形的面积通过转化成为长方形的面积。
平行四边形面积=底×高
长方形的面积=长×宽
通过转换,进行知识迁移,学生能够很快得出平行四边形面积的计算公式。
通过转化,将新知与旧知联系在一起,学生能够快速获取新知识。
(三)化曲为直,突破障碍
在小学数学学习阶段,化曲为直主要应用于曲面的求解。更直接地说,化曲为直应用于小学阶段圆的学习——求解圆的周长与面积。
在数学学习中,曲线或者曲面太难直接测量,或者说不可直接测量,这时转化思想尤为重要。
如苏教版五年级下册第二单元《圆的周长》例5:几人一组,用硬纸板剪出3个大小不同的圆,想办法量出它们的周长,再计算出周长除以直径的商,并把表格填写完整。
(四)寄数于形,提升思维
寄数于形,将数转化为形去解决问题是教学苏教版小学数学教材时常用的一种方法。对于大部分小学生来说,对于条件较多、数据之间联系复杂的问题,他们不太能够通过直接读题来分析问题,明确数量之间的关系,学生在解决问题时常常无从下手。此时,就需要将较复杂的数据类问题,通过转化形成图形问题,从而借助图形的直观,看清数之间的联系,理清数量关系,以解决问题。
苏教版教材中对以数化形的问题安排较多,主要体现在小学中、高年级解决问题的策略中。和差問题与差倍问题是苏教版四年级下册学习的一个重难点,此类问题只有数据支撑,学生通常无从下手。
如苏教版四年级下册《解决问题策略——画线段图》例1:
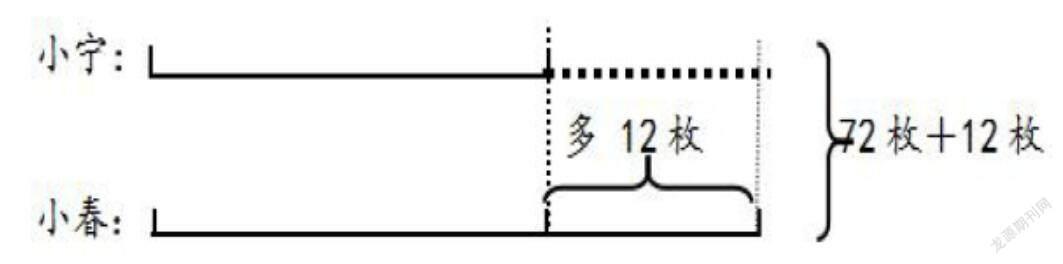
“小宁和小春共有72枚邮票,小春比小宁多12枚。两人各有邮票多少枚?”
在之前的学习中,一般告诉学生一个量以及所求量与这个量的关系,求取所求量。而在此类问题中,只告诉两个量之间的两个关系,求取这两个量,学生开始犯难。但是如果将数转化到线段图中,就简单多了。
线段图如下:
从上图中可轻易看出小宁与小春邮票数之间的关系,而解题的关键是通过将线段的“割” “补” “分”使两条线段长度一样。
以“补法”为例:通过将短的线段补齐,让小宁与小春邮票数量相等。求出小宁如果与小春邮票数相等时,共有票数为72+12=84(枚),将总邮票数平均分成两份求出小春邮票数。小宁的邮票数就求出来了。
小学数学中有些问题数量关系比较复杂,小学生解题无从下手,将问题条件寄予图形,便于分析,从而降低问题难度,便于解决问题。
二、巧用方法,渗透转化
(一)善用类比,逐步转化
类比法是将新旧内容进行比较,找出其相似点,然后根据它们之间的相似点用已知的知识推理出未知的对象。这种方法不仅有利于学生对新知的学习,更有利于学生对旧知的巩固。例如,教学“三角形的面积”时,笔者引导学生通过剪、拼等方式,将三角形转化成长方形,三角形的底一般是长方形的长,高转化为长方形的宽。通过转换,学生可自主进行三角形面积计算公式的推導。
苏教版小学数学教材的编排中处处渗透着转化思想,它们都是将没有学过的知识通过类比的方式转化成学生已有的经验或知识储备,符合学生的认知,有利于学生数学逻辑的发展。在教学中,教师应密切关注新旧知识之间的联系,在转化中让学生感受到数学知识的整体性。
(二)联想迁移,渗透转化
解决数学问题需要学生具有一定的联想与迁移能力。教师在教学中可通过联想与迁移,不断渗透转化思想方法,从而丰富学生的学习经验,提升学生的思维能力。
例如,教学苏教版六年级下册找规律课“面积的比”时,在学生探究完图形的长度比与面积比之后,接下来作为拓展,教师可引导学生思考:若两个正方体的棱长比是1∶2,它们的体积比是多少?学生通过回忆探究面积之比的过程,自然而然会联想到体积比是1∶8。从线到面的过程,可用画图的方式进行操作。从面到体的过程,更多就是通过联想,实现一个从一维图形到二维图形再到三维图形的维度迁移,学生最终可通过长度比和面积比推导出体积比。
通过联想迁移,将新的问题转化成已经学习和探索过的知识进行推导,不仅可以简化学生获得新知的过程,还可以提升学生思维能力,从而提高他们解决问题的能力,特别是对将来学习和立体图形相关的知识有极大的帮助。
(三)擅于假设,实现转化
近年来,课标对学生分析问题、解决问题的能力有进一步的要求,解决问题也成为数学教材中的重要组成部分。在小学阶段,学习解决问题的过程中,教师引导学生将问题向已有条件转化,有助于学生更直接、更有效地理清思路。其中引导学生进行假设和替换就是非常有效的方法。如六年级学习的鸡兔同笼问题,学生通过假设笼子里全是鸡或者全是兔子,通过腿产生的差量去求解,就能将未知的问题转化为已知条件——鸡和兔子的只数。通过假设,实现转化,将问题简化。
作为数学学习中的重要思想,转化对提升学生的数学思维能力起着巨大的作用。根据教材的编排以及学生已有的认知结构,教师在日常教学中要积极钻研,读懂教学中蕴含的转化思想。同时,教师应当了解小学数学各知识之间的联系,引导学生进行联想,并利用转化的思想举一反三,获得知识的拓展和思维的提升。教师在教学中不断渗透转化的思想,能使教与学达到事半功倍的效果。
【参考文献】
[1]黄丽琳.激发小学生数学应用题学习兴趣的有效研究[J].儿童大世界:教学研究,2017(01):145.
[2]全云.小学数学应用题教学中存在的问题及优化策略探究[J].中国校外教育,2018(10):127-130.
[3]韩志忠.小学高年级数学应用题解答能力的培养策略[J].课程教育研究,2019(38):155-156.
[4]中华人民共和国教育部.义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.

