改进的GA与BP-PID融合移动机器人轨迹跟踪研究

石秀敏，孙建康，邓三鹏

（天津职业技术师范大学机器人及智能装备研究院，天津 300222）

随着人工智能和移动机器人技术的发展，“人工智能+移动机器人”已经成为国内外研究的热点[1]。三轮全向轮式移动机器人不仅能够完成自身的零半径转向控制，可以达到任何期望的方向，而且具有机动性高，运动敏捷的特点，对狭小空间有很好的适应性，得到了越来越广泛的应用[2]。同时，为了更好地完成任务，需要机器人精确跟踪预定的轨迹，因此全向移动机器人核心技术的轨迹跟踪问题，受到了学术界和实践者的广泛关注[3]。

由于机器人传感器噪声、外界干扰和未建模参数等因素的干扰，针对全向轮式移动机器人的轨迹跟踪控制器的设计是非常具有挑战性的[4]。为了提高全向移动机器人的轨迹跟踪精度，业界已经出现了各种各样的方法，如控制系统在模型预测控制律下，可以按照指定的轨迹进行跟随，但需要系统精确的动力学和运动学模型，且分析过程较繁琐，不利于分析和求解[4-6]。采用滑膜控制器不依赖于系统的数学模型，可以针对突变参数做出快速反应，拥有很强的适应性，但由于其自身的抖振问题增加了在轨迹跟踪控制上的应用难度[7]。使用Backstepping方法可以实现轨迹跟踪的全局一致稳定性，但是需要提前给定控制器的增益，而该增益是不变的，当给定的参考轨迹发生突变时，再使用能使全局稳定的控制器增益，就很难取得较好的控制效果[8]。自适应控制可以不断地获取系统自身的状态，然后及时进行识别，根据识别结果给出响应的输出，使得调控性能达到最优，缺点是参数的选取比较繁琐[9]。模糊控制方法具有一定的鲁棒性，但是模糊规则主要是人为制定，可能存在考虑不全面的因素，并且模糊控制不能够自我学习和调整，因此静态误差很难消除[10]。神经网络虽然具有诸多优点，但是由于神经网络的初值采用随机复制策略，这就导致学习速度慢并且存在局部极小值的问题，进而影响网络的预测能力[11]。传统的PID控制器可以直接根据偏差调整控制量，控制结构简单，调整方便，但是其参数值总是固定不变，不能根据当前所处的环境进行动态调整[12]。综上所述，现有的轨迹跟踪控制器的设计大都比较复杂或者其性能不能很好地跟踪参考轨迹，因此本文使用基于改进的遗传算法和BP-PID进行融合作为机器人的控制器[13]，并结合机器人的运动学进行仿真实验，验证控制算法的轨迹跟踪精度。

1 三轮全向移动机器人的数学模型

无论是通常使用的四轮自行车模型还是两轮的差速驱动模型，其运动轨迹主要由直线和圆弧组成，运动轨迹比较复杂，而不能使其达到点到点的跟踪要求，全向轮式移动机器人可以达到一面直线运动，同时又能进行转向的效果，其运动轨迹可以归纳为折线[14]。本节分析了全向轮式移动机器人的运动学模型，为后期的轨迹跟踪控制器的设计做铺垫。

1.1 运动学模型

全向轮式移动机器人的数学模型如图1所示。

图1 全向轮式移动机器人的数学模型

图1中，定义世界坐标系X-O-Y固定于机器人工作的平面，机器人坐标系Xe-Oe-Ye固定于机器人的重心Oe处，L为3个轮子相对于机器人中心的距离，VA、VB、VC分别为3个轮子的速度方向。设p=（x yθ）T，q=（v w）T，（x y）为在X-O-Y坐标中的位置；θ为全向轮式移动机器人的方向角；v为全向轮式移动机器人的输入线速度；w为全向轮式移动机器人的输入角速度。则其运动学方程可以表示为

考虑全向轮式移动机器人3个轮子的转速，即VA、VB、VC大小与控制输入q=（v w）T之间的变换关系。即可得到全向轮式移动机器人的运动学模型，ψ=60°为机器人轮速方向与等边三角形一条边的夹角，见图1。Vx为机器人在自身坐标系下Xe方向的速度；Vy为机器人在自身坐标系下Ye方向的速度。则机器人在自身坐标系下的运动学方程为

为了便于分析，需要把机器人在自身坐标系下的运动学方程转化为世界坐标系下的运动学方程，设机器人在世界坐标系下的速度为V=（VgxVgywg）T，那么由自身坐标系下的运动学方程转化为世界坐标系下的运动学方程的变换关系如下

联立式（2）、（3）便可得到世界坐标系下机器人速度和角速度转换为其自身3个轮子的转速，即为求得的机器人运动学模型

式中：A为-cosψcosθ；B为sinψsinθ；C为-cosψsinθ；D为sinψcosθ；V=（VgxVgywg）T中的Vgx、Vgy分别为世界坐标系中V沿X轴和Y轴的2个分量；wg为w。

1.2 总体控制结构

为了使全向移动机器人对轨迹进行精确的跟踪，结合上文给出的全向移动机器人的运动学模型，设计了基于改进GA的BP-PID控制器，本文总体的控制器以及系统的运行结构设计如图2所示。

图2 机器人的轨迹跟踪的总体控制图

从图2可知，总体控制轨迹跟踪控制器和机器人运动学模型2部分组成，其中，xr、yr、θr分别为参考路径上每个点的x、y值以及当前点的斜率；x、y、θ分别为机器人当前位置的x、y值及其航向角；xe、ye、θe分别为机器人当前点相对于参考点之间的误差以及航向角之间的误差；cur为参考路径当前点的曲率；kp、ki、kd为PID控制器中的3个控制量。

首先，使用遗传算法优化得到神经网络需要的初始值后，BP神经网络通过梯度下降法不断地对PID的3个参数进行拟合。其次，当PID控制器得到优化后的kp、ki、kd参数，结合位姿误差以及参考轨迹的曲率，给出3轮全向移动机器人的速度和角速度，并把这2个参数输入到机器人的运动学模型中，进而得出机器人当前在世界坐标系中的位姿。再返回到参考轨迹处，并与参考轨迹的下一个点进行比较。最后，依次循环使得机器人精确地跟踪预定轨迹。

2 算法的改进

虽然神经网络可以用任意精度拟合任意给定的函数，但由于BP算法存在陷入局部最优值的问题，进而导致出现错误的工作模式。而遗传算法是基于生物进化的自适应优化方法，利用适应度函数决定进化方向，并且在种群的全局范围内进行寻优，具有全局寻优性。因此考虑使用遗传算法全局寻优的优点弥补BP网络易陷入局部最优值的缺点，其原理就是利用遗传算法寻找BP网络的初始权值，进而避免因随机赋值而导致BP网络出现局部最优解的现象。因此，将2种算法融合以提高网络的训练速度和输出的正确性，优化流程如图3所示。

图3 GA优化BP网络总体框图

改进的遗传算法主要流程如下：

（1）种群初始化

首先把神经网络随机产生的初始权值作为遗传算法的一个个体，并在在解空间内随机产生N个体，为了便于计算机的高效计算，采用二进制对每个个体进行编码。

（2）适应度函数

因为适应度函数决定着整个群体的进化方向，淘汰劣质个体，保留优质个体，保证群体向着好的方向发展。求出误差的均方根值再求倒数，即可得出个体的适应度值F为式中：T为神经网络的训练次数；yi为BP神经网络第i次的预测输出；oi为第i次的期望输出，误差值越小，适应度值越高。

（3）选择操作

选择操作的方式有很多，本文使用轮盘赌法对每个个体进行选择，只需要按照轮盘赌法的选择公式进行选择即可，选择公式如下

式中：Fi为个体i的适应度值；N为种群个体数目。

（4）交叉操作

从染色体的某一位开始向后直到末尾，进行2个染色体之间的基因交叉互换，有助于父代优良的基因传递给下一代，进而产生更加优秀的个体。遗传算法染色体交叉图如图4所示。

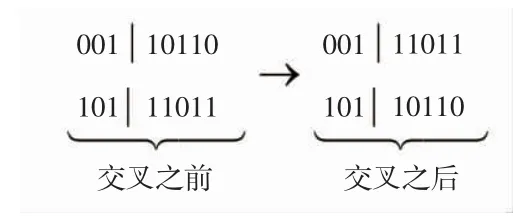
图4 遗传算法染色体交叉图

（5）变异操作

根据生物学上的基因突变原理，也是在染色体上的某个基因进行突变，因按照二进制进行编码，所以随机对某一位基因进行取反操作，进而产生新的染色体。遗传算法染色体变异图如图5所示。

图5 遗传算法染色体变异图

虽然遗传算法具有全局寻优性能，但是在其实际的运用过程中仍存在过早收敛于局部最优的现象。究其原因就在于其固定的交叉和变异概率，为了解决该问题，避免过早出现种群过于单一现象，改进方法的基本原理为：前期让其保持较低的交叉概率和较高的变异概率，以便在解空间内全局寻优，在优化的后期，这2个概率采用与前期相反的操作，有助于种群快速找到最优解，见式（7）和（8）。

pc∈[pc2pc1]为交叉概率以及交叉概率所属的最小最大值范围；pm∈[pm2pm1]为变异概率以及变异概率所属的最小最大值范围；F′为两交叉的染色体中适应度较大个体的适应度值；F为当前变异个体的适应度值；Favg、Fbest分别为种群中的平均适应度值和最大适应度值。

3 仿真实验与分析

为了验证基于改进GA与BP-PID融合算法对机器人轨迹跟踪的有效性，本文使用Matlab 2020b作为仿真实验环境，创建了移动机器人模拟运行的预定轨迹，并按照控制算法流程编写了移动机器人轨迹跟踪的控制代码，在控制算法的设计中，遗传算法的种群大小和遗传代数都设置为50，其交叉和变异概率使用改进后的概率公式进行动态计算，其中，pc1=0.9，pc2=0.6，pm1=0.1，pm2=0.01，并采用10位二进制码表示每个个体，然后对BP网络的结构参数进行确定，BP网络采用3层结构，7个输入节点，8个中间节点，3个输出节点，输出节点分别是需优化的kp、ki、kd三个参数。为了进行对比分析，设置常规PID控制器参数，kp=1.0、ki=0.5、kd=0.25，最后是全向轮式移动机器人初始参数设定：初始速度v=8.3 m/s，航向角采用直角坐标系进行表达，初始位姿为（x yθ）=（0，0，0）。

在PID轨迹跟踪控制算法的基础上添加了神经网络，使用神经网络自动拟合PID的参数，实验结果如图6所示。

图6 BP-PID控制器和PID控制器对轨迹跟踪效果对比图

机器人的运动轨迹是由几个自定义的点位，并结合样条曲线生成一条光滑的曲线。以上各图中黑色虚线表示机器人的预定路径，红色实线表示机器人根据不同控制算法生成的实际运行轨迹，蓝色实线表示机器人当前点在x或y方向上距离参考点的偏差。对比图6（a）、（b）可知，图6（b）的轨迹跟踪误差较大，不能实现PID参数的自动调节，而图6（a）由于添加了神经网络，可对参考路径的曲率进行辨别，进而实现自动调整ID参数的作用，同时从图6（c）、（d）和图6（e）、（f）可以发现，使用神经网络控制器相比单纯使用PID控制器在x和y方向上的偏差更小。通过对比得出，经过BP网络拟合得出的运行轨迹比单纯使用PID控制器得出的控制效果要有很大的改善，但是由于神经网路的初始权值是随机赋值的，网络的拟合结果可能存在局部最小值，为了改善该问题，使用遗传算法先对网络的初始权值进行寻优，以保证网络拟合时收敛于全局最小值。

为了消除网络随机赋值对跟踪效果的影响，把改进之后的遗传算法应用在网络权值的初始化上，GABP-PID控制器和BP-PID控制器轨迹跟踪效果对比如图7所示。

图7 GA-BP-PID控制器和BP-PID控制器轨迹跟踪效果对比图

图7（a）、（c）、（e）为使用改进GA与BP-PID融合之后的控制器得出的运行轨迹，图7（b）、（d）、（f）为使用BP-PID控制器得出的运行轨迹。从图7可以看出，机器人的实际轨迹几乎贴近预定的参考轨迹，机器人在y轴方向的误差更小，并且经过多次试验发现基于改进GA与BP-PID融合之后的算法运行效果具有稳定性，而使用BP-PID控制器运行的效果具有不确定性，误差难以控制，因此基于改进GA与BP-PID融合之后的算法在轨迹跟踪精度和输出结果的准确性上有了很大的提高。使用PID控制器和基于改进GA与BP-PID融合的控制器的对比实验，其轨迹跟踪的结果如图8所示。

图8 GA-BP-PID控制器和PID控制器轨迹跟踪效果对比图

图8中，由基于改进GA与BP-PID融合控制器得出图8（a）、（c）、（e），由PID控制器得出图8（b）、（d）、（f）。对比图8（a）、（b）可知，单纯使用PID控制器进行轨迹跟踪，跟踪精度差，易出现超调，使得追踪效果不稳定，而使用改进之后的PID算法，即基于改进GA与BP-PID融合控制器能够明显地克服这些问题，轨迹跟踪的效果不易超调，比较稳定。同时，对比x方向的图8（c）、（d）和y方向的图8（e）、（f）可知，使用改进后的PID算法误差更小。因此，相比传统的PID算法，基于改进GA与BP-PID融合控制算法的误差更小，更能精确地跟踪预定的轨迹。

4 结语

本文结合移动机器人的运动学模型，设计了移动机器人的轨迹跟踪控制器，基于改进GA与BP-PID融合为主要控制算法，并对该算法进行了模拟仿真，得出结论如下：使用固定的PID参数进行轨迹跟踪，虽然可以达到一定的效果，但是仍然出现了很大的偏差，而BP网络易陷入局部最优解，不能对PID参数进行很好地拟合。因此，为了提高网络的全局寻优性能，使用GA优化BP网络的初值，然后再使用BP网络进行PID参数的拟合。得到的效果明显比单独使用BP进行优化更能精确地跟踪路径，通过Matlab模拟仿真，验证了使用基于改进GA与BP-PID融合控制算法能够使移动机器人对预期轨迹进行精确地跟踪。