废旧锂电池梯次利用质量控制研究

李洛康，顾巧论

（天津职业技术师范大学经济与管理学院，天津 300222）

随着以锂离子电池为动力的新能源汽车快速普及，汽车上退役下来的各种锂电池如果不及时处置，将会成为新能源汽车产业健康发展的阻力。周航等[1]分析了国家层面发布的汽车动力电池回收利用政策和标准，梳理了我国和发达国家在电池回收方面开展的一系列工作。动力电池退役处置包括梯次利用和再生利用，新能源汽车上退役的磷酸铁锂电池，当各项性能良好且电池容量不低于80%时是具有梯次利用价值的[2]。高震等[3]根据放电深度区间与端电压衰减快慢的关系以及多次循环实验下电池的容量衰减程度等标准，将退役锂离子电池的健康状态划分为不同的区间，以实现梯次利用的效率最大化。吴远忠等[4]指出做好锂电池筛选分类与重组的工作，以确保梯次利用电池组内部电池单元性能的一致性，将是梯次利用的关键。文献[5-8]分析了我国锂电池梯次利用在新能源汽车充电、通信、储能、辅助调频等领域的研究进展。李建林等[9]对退役电池梯次利用过程中的分类筛选、重组、热失控特征、均衡控制及电极材料回收等关键技术进行了研究，分析了不同方法及控制策略的优缺点。文献[10]以奥迪A3的锂离子电池为例，提出了基于电池健康状态的不同回收拆解模型，证明了该模型的可行性和有效性，为锂电池回收再制造过程提供了重要的参考。Standridge等[11]通过构建数学模型，研究了从新能源汽车上退役下来的锂离子电池的再制造、再利用和回收能力。Tao等[12]以上海工业园区的电力负荷为例，采用粒子群优化和成本效益模型，分析了光伏储能系统中电池在整个生命周期的经济性，研究结果表明，光伏储能系统中不同类型电池由大到小的经济顺序为新型锂电池、再制造锂电池和铅酸电池。张玉春等[13]通过构建再制造优先的质量控制系统动力学模型，研究了制造商和销售商的最优质量投资决策，并采用收益共享契约进行优化。Kim等[14]对闭环供应链再制造质量控制进行了相关研究，认为回收产品质量的不确定性会对再制造系统的绩效和质量产生很大的影响，因此建立了考虑回收产品质量的再制造质量控制模型，以控制再制造产品的质量。Chao等[15]研究了一种信息不对称情况下的方案，该方案不仅显著降低了制造商因信息不对称而产生的成本，而且还提高了产品质量。冯昱[16]通过系统动力学仿真分析发现：制造商通过设置合理的质量惩罚比例、成本分摊比例和抽检比例，可以有效约束销售商机会主义行为，提高闭环供应链回收品质量水平。基于上述研究，本文将应用Vensim PLE构建废旧锂电池回收再制造的系统动力学模型，研究制造商作为主导者如何采取措施来降低检测误差，提高重组电池质量，同时也要保证拆解中心的经济效益。

1 模型基本描述

构建由回收商、制造商和拆解中心组成的废旧锂电池三级逆向供应链模型。回收商负责废旧锂电池的回收，拆解中心负责废旧锂电池的全部拆解、检测，制造商负责重组和售卖。拆解检测中心将电池包拆解为电池单体后，并根据电池单体性能大致进行分类：各项性能都很好的称之为一级电池单体；各项性能一般的称之为二级电池单体；无法再利用的电池单体称之为不可梯次利用电池单体。拆解检测中心将一级电池单体和二级电池单体送至制造商处进行重组，不可梯次利用电池单体直接处理掉。制造商对一级电池单体和二级电池单体直接进行重组，在这个过程中拆解中心由于检测技术或者利己主义，谎报质量信息，造成一定的误差，如把二级电池单体检测为一级电池单体，并出售给制造商，制造商不进行质量检测而直接重组，此时会造成重组电池包的不一致性。在梯次利用过程中，单体电池的不一致性严重影响到重组电池模组的可用容量、充放电性能、寿命及安全等多方面的性能，它是决定电池组可用容量和电池使用寿命的关键因素。

1.1 模型假设

（1）本文只考虑一种产品正常使用结束后的回收和再制造问题，并且该产品只能再制造一次。闭环供应链各节点成员订货率由自身库存调整率和下级成员需求率决定。

（2）该模型由制造商主导，为控制一级电池单体和二级电池单体质量，制造商采取抽检的方式对2种电池单体进行质量检测，抽检比例为r（0≤r≤1），若被抽检的单体质量合格（一级电池单体中无二级电池单体），制造商则按照原价向拆解检测中心支付；不合格部分制造商将对拆解检测中心进行惩罚；未被抽中的部分若质量不合格，制造商认其合格而进行重组售卖，制造商会产生一定的潜在损失。

1.2 废旧锂电池回收再制造系统动力学模型

1.2.1 模型中函数关系式

废旧锂电池回收再制造存流图如图1所示。

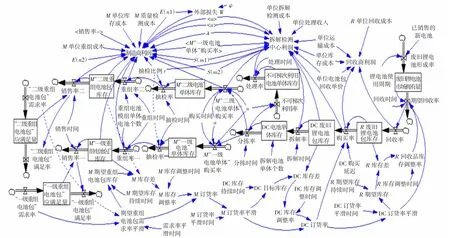
图1 废旧锂电池回收再制造存流图

在系统动力学模型中，方程主要表示各变量之间存在的关系，该模型主要仿真分析检测误差率对系统的影响，以及制造商通过采取抽检和质量惩罚2种措施增加利润和降低检测误差，主要方程如下：

制造商利润=（销售率二×E（n2）+销售率一×E（n1））-IF THEN ELSE（抽检比例r=0，S（m1）×M“一级电池单体购买率+S（m2）×M“二级电池单体”购买率，S（m1）×M“一级电池单体”购买率+S（m2）×M“二级电池单体”购买率-（M“二级电池单体”购买率+M“一级电池单体”购买率）×抽检比例r×a×u×S（m2）×λ+（M“一级电池单体”购买率+M“二级电池单体”购买率）×抽检比例r×M质量检测成本）-（M单位库存成本×（M“一级重组电池包”库存+M“二级重组电池包”库存）+M单位重组成本×（重组率一+重组率二）+IF THEN ELSE（抽检比例r=0，IF THEN ELSE（a＞0，潜在损失W，0），IF THEN ELSE（a＞0，（1-抽检比例r）×潜在损失W，0））） （1）

拆解检测中心利润=IF THEN ELSE（抽检比例r=0，（单位处理收入×处理率+M“一级电池单体”购买率×S（m1）+M“二级电池单体“购买率×S（m2）），（单位处理收入×处理率+M“一级电池单体”购买率×S（m1）+M“二级电池单体“购买率×S（m2））-（M“二级电池单体”购买率+M“一级电池单体”购买率）×抽检比例r×a×u×S（m2）×λ）-购买率×（单位运输成本+单位电池包回收单价）-DC废旧锂电池包库存×单位库存成本-拆解率×单位拆解检测成本（2）

式中：M质量检测成本为制造商抽检时，每检测一个电池单体所需成本；M单位库存成本为制造商单位电池包库存成本；M单位重组成本为制造商每重组一个电池包时所需成本；单位处理收入为拆解检测中心每处理一个不可梯次利用电池单体时的收入（拆解检测中心可以将不可梯次利用电池单体送至专业化拆解回收企业进行金属材料回收）；单位运输成本为拆解检测中心运输单位电池包的运输费用；单位电池包回收单价为拆解检测中心从回收商处回收单位电池包的费用；单位库存成本为拆解检测中心单位电池包库存成本；单位拆解检测成本为拆解检测中心每拆解和检测单位电池包的费用。

1.2.2 模型中参数说明

废旧锂电池回收再制造存留图中主要有水平变量、速率变量、辅助变量和常量，部分变量说明如下：u为拆解后全部电池单体中一级可梯次利用电池单体比例和二级可梯次利用电池单体比例；a为二级电池单体检测为一级电池单体比例；r为制造商抽检比例；S（m1）为制造商一级可梯次利用电池单体单位回收价格；S（m2）为制造商二级可梯次利用电池单体单位回收价格；E（n1）为制造商一级可梯次利用电池包单位出售价格；E（n2）为制造商二级可梯次利用电池包单位出售价格；φ为潜在损失系数；λ为制造商对拆解检测中心的质量惩罚系数。供应链参数设置如表1所示。

表1 三级逆向供应链参数设置

2 仿真分析

仿真分析主要包括参数a灵敏度分析，以及抽检比例r和质量惩罚系数λ对制造商和拆解检测中心利润的影响。其中，INTIAL TIME为0，FINAL TIME为100周，TIME STEP为1周。

2.1 对检测误差率a进行灵敏度分析

为确保所构建的废旧锂电池回收再制造系统动力学模型能解决研究的问题，需要对检测误差率a进行灵敏度分析，仿真结果如图2和图3所示。

图2 检测误差率a对制造商“一级电池单体”库存影响

图3 检测误差率α对制造商“二级电池单体”库存影响

从图2和图3可以看出，随着检测误差率a的增大，拆解检测中心会把更多的二级电池单体检测为一级电池单体，造成二级电池单体数量减少，一级电池单体数量增多。当2种电池单体出售给制造商，制造商二级电池单体库存会逐渐减小，一级电池单体库存逐渐增大，模型符合现实情况。

2.2 制造商可接受的潜在损失范围

检测误差会造成重组电池包的不一致性，在存在一定检测误差的条件下，如果制造商没有完全检测而进行重组销售时，会因质量原因影响重组锂电池销售市场和梯次利用市场的发展，造成潜在的损失，因此制造商需要仿真分析其潜在损失范围。不同潜在损失系数对制造商利润变化如图4所示。

图4 不同潜在损失系数对制造商利润变化

从图4可知，随着潜在损失系数φ的增大，其利润逐步降低，当潜在损失系数φ＞4时，制造商亏损。由此可知，严格的质量检测是制造商保证重组电池质量安全，减小其潜在损失的有效方法。

2.3 抽检比例r和质量惩罚系数λ对制造商和拆解检测中心利润的影响

假设潜在损失系数φ=4时，制造商为了谋利，会采取2种措施：①加大抽检比例；②与拆解检测中心制定质量惩罚系数。分析抽检比例和质量惩罚系数λ对二者利润的影响。

2.3.1 抽检比例r对制造商和拆解检测中心利润的影响

抽检比例r对制造商和拆解检测中心利润变化影响如图5和图6所示。

图5 抽检比例r对造商利润影响

图6 抽检比例r对拆解检测利润影响

提高抽检比例r，制造商利润增大。这是因为随着抽检比例的提高，制造商会发现越来越多的不一致电池单体，造成的潜在损失就会越小，且减小的潜在损失大于抽检成本。制造商对拆解检测中心的质量惩罚系数λ=0时，抽检比例的变化对拆解检测中心利润没有影响，制造商只通过决策抽检比例r的取值大小，不会使拆解检测中心主动降低检测误差率。

2.3.2 质量惩罚系数λ对制造商和拆解检测中心的影响

制造商提高抽检比例会减小其潜在损失，增加利润，但是抽检比例r变化对拆解检测中心利润无影响，拆解检测中心不会主动去降低检测误差。因此，考虑制造商与拆解检测中心制定质量惩罚措施，仿真分析质量惩罚系数对二者利润的影响。在检测误差率a=30%，抽检比例为50%的条件下，质量惩罚系数λ取值范围＞1时，对制造商和拆解检测中心利润的影响如图7和图8所示。

图7 质量惩罚系数λ对制造商利润影响

图8 质量惩罚系数λ对拆解检测中心利润影响

由图7和图8可知，质量惩罚系数λ取值范围越大，制造商利润越大。当λ=2时，制造商利润趋近于a=0和r=0时的利润，制造商利润达到无检测误差率时的利润水平；当λ＞2时，制造商利润高于无检测误差率时的利润水平，拆解检测中心利润随着质量惩罚系数λ增大而减小，且逐渐低于无检测误差率时的利润；当λ＞3时，拆解检测中心处于亏损状态。当检测误差率a=0.1时，质量惩罚系数λ＜1，对拆解检测中心和制造商利润影响变化均不明显，拆解检测中心不会降低检测误差率。从图中可知，λ最佳取值范围为（1，3），制造商在此范围内可以调控质量惩罚系数λ，使得拆解检测中心利润主动降低检测误差率a。

2.4 制造商不同检测误差率下的最优抽检范围

上述内容仿真分析了增大抽检比例r和质量惩罚系数λ对制造商都是有利的，但是抽检比例r达到1时会造成重复检测，增加系统检测成本，因此制造商需要分析在质量惩罚系数一定的条件下，不同检测误差率下的最优抽检范围。在检测误差率a=20%，质量惩罚系数λ=3时，抽检比例对制造商和拆解检测中心利润的影响如图9和图10所示。

图9 抽检比例r对制造商利润影响

图10 抽检比例r对拆解检测中心利润影响

从图9和图10可知，随着抽检比例r增大，制造商利润增大，当抽检比例r=0.5时，制造商利润达到检测误差率a=0时的利润，拆解检测中心利润低于检测误差率a=0时利润，此时如果拆解检测中心为追求高利润，便会主动降低检测误差率。因此，检测误差率a=0.2时，制造商最优抽检比例r=0.5。通过仿真分析可知，当检测误差率a=0.1，制造商抽检比例r达到0.8时，制造商利润达到检测误差率a=0时的利润，拆解检测中心利润低于检测误差率a=0时利润，因此检测误差率a=0.1，制造商最优抽检比例为0.8。

3 结语

本研究构建了以制造商为主导的废旧锂电池再制造系统动力学模型，仿真分析了制造商可接受的质量惩罚损失范围、抽检比例r和质量惩罚系数λ对制造商和拆解检测中心的影响，以及制造商的最优抽检比例。研究表明：制造商通过增大抽检比例可以降低外部损失，但是抽检比例r的变化不影响拆解检测中心利润，拆解检测不会主动降低检测误差率。此外，随着抽检比例的增大，会造成制造商和拆解检测中心重复检测，增加供应链系统检测成本。基于此，制造商可以与拆解检测中心制定质量惩罚系数，通过调节质量惩罚系数λ，不仅可以增大制造商利润，还可以约束拆解检测中心，使其主动降低检测误差率a。在质量惩罚系数λ=3时，制造商可以得到不同检测误差率下的最优抽检比例r的值。