求解非单调变分不等式的一种修正二次投影算法

蒋铃钰，叶明露

(西华师范大学 数学与信息学院，四川 南充 637009 )

本文考虑的经典变分不等式的模型VI(F,C)如下：求x*∈C使得

〈F(x*),y-x*〉≥0,∀y∈C，

(1)

其中，C⊆Rn是闭凸集，F∶C→Rn是一个连续映射。其解集记为S。用〈·,·〉和‖·‖来分别表示Rn中的内积和范数。变分不等式在交通、经济、微分方程及优化等领域都有较为广泛的应用[1-4]。投影算法是求解VI(F,C)的一种简单有效的算法。因此，本文主要关注投影类算法来求解VI(F,C)问题。Goldstein[5]和Levitin-Polyak[6]介绍了一种简洁的投影算法，其算法如下：

xk+1=PC(xk-βF(xk))，

(2)

其中，β>0为步长。该算法的全局收敛性需要映射F在C上Lipschitz连续且满足强单调性的条件。但强单调的假设条件限制了算法(2)的运用。因此为了将算法(2)中映射F的强单调性削弱为单调性或者伪单调性，Korpelevich[7]提出了一种新的外梯度投影算法，其结构如下：

(3)

尽管该算法在每次迭代中需要向可行集C作两次投影，但该算法的收敛性只需要映射F在C上Lipschitz连续且伪单调。因此，外梯度投影算法受到了众多学者的关注和研究[8-10]。为了削弱映射F的Lipschitz连续性，Iusem[1]引入了Armijo型线性搜索。这不仅可以得到一个更长的步长，还可将映射F在C上的Lipschitz连续削弱为连续，详细发展过程还可参见[2-13]。最近，Ye和He[14]在式(1)的对偶变分不等式的解集

(4)

非空的假设条件下，提出了一种二次投影算法，并证明了该算法的全局收敛性。因为该算法没有假设F具有任何的单调性，从而适用于求解SD≠∅的非单调的变分不等式问题。该算法的新迭代点计算如下：

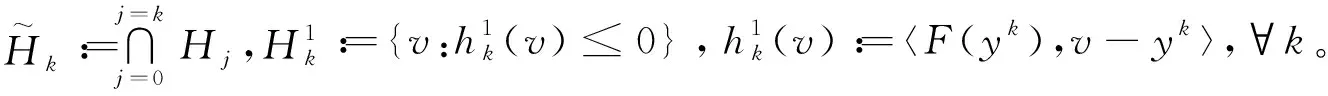
Konnov[15-16]提出了求解伪单调VI(F,C)问题的Combined relaxation methods算法。其新迭代点xk+1由当前迭代点xk向能严格分离当前迭代点和解集S的超平面作投影来生成，这使得

dist(xk+1,S)≤dist(xk,S),∀k，

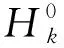
xk+1=PC∩Ck(xk)，

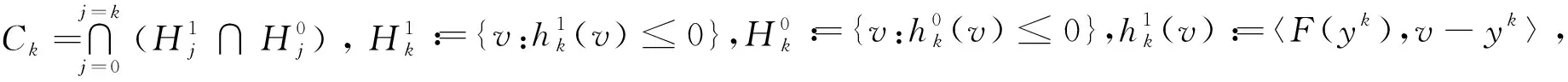
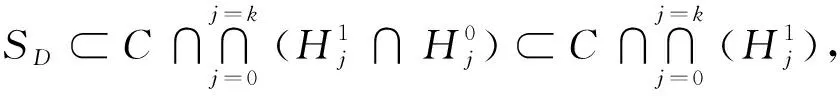
xk+1=PC∩Ck(xk)，

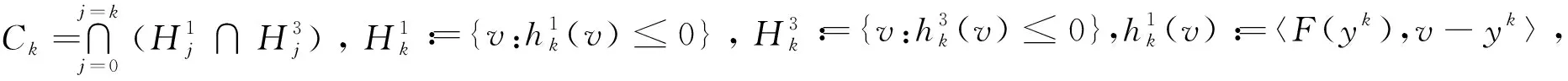
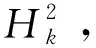
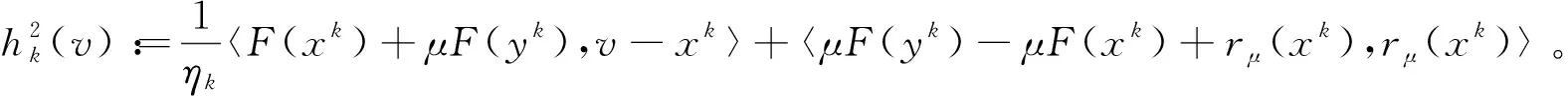
1 预备知识

首先回顾一些投影算子的定义、性质及相关结论。

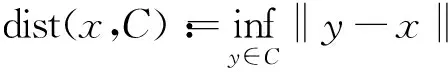
引理1[14]设C是Rn中的闭凸集，F:C→Rn是一个连续映射，则SD⊂S。

引理2[19]设K是Rn中的非空闭凸集且xk+1=PK(xk)，则对∀x*∈K，都有以下不等式成立:

‖xk+1-x*‖2≤‖xk-x*‖2-‖xk+1-xk‖2。

定义2对∀μ>0，记问题(1)的自然残差映射为rμ(x)∶=x-PC(x-μF(x))。

引理3[13]设μ>0，则x*∈S⟺‖rμ(x*)‖=0。

引理4[19]设x∈C且μ>0，则有以下不等式成立：〈F(x),rμ(x)〉≥μ-1‖rμ(x)‖2。

定义3设映射F:C⊂Rn→Rn，称F在C上Lipschitz连续，若对任意的x,y∈C都存在M>0使得‖F(x)-F(y)‖≤M‖x-y‖。

引理5[19]设C是Rn上的闭凸集，h(x)是Rn上的实函数，记K∶={x∈C:h(x)≤0}。若K非空，h在C上Lipschitz连续且模为θ>0，则对∀x∈C，都有以下不等式成立：dist(x,K)≥θ-1max{h(x),0}。

2 算法及初步结果

先给出改进的二次投影算法，称其为算法1，如下:

算法1选取x0∈C为初始点，参数σ∈(0,1)，γ∈(0,1)且μ∈(0,σ-1)。设k=0。计算

zk∶=PC(xk-μF(xk))。

步骤1计算rμ(xk)=xk-zk。若rμ(xk)=0，则停止；否则，转到下一步。

步骤2计算yk=xk-ηkrμ(xk)，其中ηk=γmk，而mk是使得以下不等式成立的最小非负整数m:

总之，我们的研究结果表明：按规律联合按需服用西地那非能安全有效地改善合并PE的ED患者的勃起功能，如勃起功能获得改善，多能使患者的PE得到明显改善。PE未能改善的患者多为中重度ED，虽然这部分患者IELT无明显改善，但是却能显著改善他们的配偶性生活满意度。

〈F(xk)-F(xk-γmrμ(xk)),rμ(xk)〉≤σ‖rμ(xk)‖2。

(5)

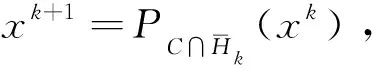
令k=k+1，并返回步骤1。

在后文中，只假设以下2个条件成立：A)F:C→Rn是连续的，C⊂Rn是非空闭凸集；B)SD≠∅。

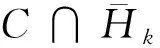
首先，说明步骤2中的线搜索成立。

引理6对∀k∈N，都存在一个非负整数m满足(5)式。

〈F(xk0)-F(xk0-γmrμ(xk0)),rμ(xk0)〉>σ‖rμ(xk0)‖2。

(6)

又因为F是连续的，γ∈(0,1)，所以

〈F(xk0)-F(xk0-γmrμ(xk0)),rμ(xk0)〉→0(m→∞)。

因此，由(6)式可得0≥σ‖rμ(xk0)‖2。又因为σ∈(0,1)，故只有‖rμ(xk0)‖=0，这与步骤1中‖rμ(xk0)‖≠0矛盾。故对∀k∈N，都存在一个非负整数m满足(5)式。

接下来，讨论算法1中的超平面的性质。

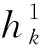
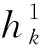
(7)

由(5)式和引理4可得

ηk〈F(yk),rμ(xk)〉≥ηk〈F(xk),rμ(xk)〉-ηkσ‖rμ(xk)‖2≥ηkμ-1‖rμ(xk)‖2-ηkσ‖rμ(xk)‖2，

(8)

因此结合(7)式和(8)式可得

(9)

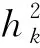
=〈μF(yk)-μF(xk)+rμ(xk),rμ(xk)〉

=μ〈F(yk),rμ(xk)〉-μ〈F(xk),rμ(xk)〉+‖rμ(xk)‖2，

(10)

由(5)式可得

μ〈F(yk),rμ(xk)〉≥μ〈F(xk),rμ(xk)〉-μσ‖rμ(xk)‖2，

(11)

进而由(10)式和(11)式有

≥μ〈F(xk),rμ(xk)〉-μσ‖rμ(xk)‖2-μ〈F(xk),rμ(xk)〉+‖rμ(xk)‖2

=(1-μσ)‖rμ(xk)‖2>0。

2)因为yk=xk-ηkrμ(xk)=(1-ηk)xk+ηkzk，且xk∈C(∀k)，故yk∈C(∀k)。因此，可知

(12)

又由xk∈C及SD的定义可知

(13)

另一方面，有

(14)

其中的不等式由(12)式可得。因此，由(13)式和(14)式可得

(15)

进而由(15)式可得

(16)

又由引理4可得

-μ〈F(xk),rμ(xk)〉≤-μ·μ-1‖rμ(xk)‖2。

(17)

因此，结合(16)式和(17)式可得

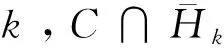
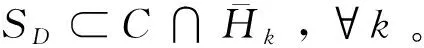
3 收敛性分析

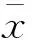
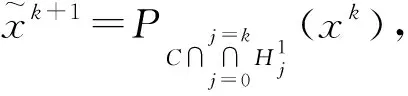
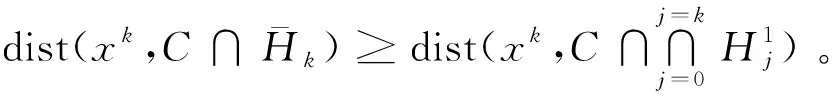
定理1若SD≠∅，则由算法1所生成的无穷序列{xk}收敛到SD≠∅的一个解。

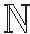
(18)

因此序列{‖xk-x*‖2}是一个递减序列，从而收敛且序列{xk}有界。对(18)式取极限(k→∞)可得

(19)

因为序列{xk}有界，则∃M>0使得‖xk‖≤M。又因为在有限维空间中连续函数映射的有界集为有界集，因此由F的连续性可得序列{F(xk)}有界，则∃M1>0使得‖F(xk)‖≤M1。故由范数的三角不等式有‖xk-μF(xk)‖≤‖xk‖+μ‖F(xk)‖≤M+μM1≤2M2，其中M2=max{M,μM1}，因此可以得到序列{xk-μF(xk)}有界。再由zk=PC(xk-μF(xk))和投影算子的连续性可知序列{zk}有界，即∃M3>0使得‖zk‖≤M3。因为rμ(xk)=xk-zk，则由范数的性质有‖xk-zk‖≤‖xk‖+‖zk‖≤M+M3≤2M4，其中M4=max{M,M3}，因此可以得到序列{rμ(xk)}有界，即∃M5>0使得‖rμ(xk)‖≤M5。又因为yk=xk-ηkrμ(xk)，其中ηk=γm，γ∈(0,1)，则ηk≤1，所以ηk‖rμ(xk)‖≤M5，因此由范数的性质有‖xk-ηkrμ(xk)‖≤‖xk‖+ηk‖rμ(xk)‖≤M+M5=2M6，其中M6=max{M,M5}，故序列{yk}有界。又因为序列{xk}和{yk}有界，且在有限维空间中连续函数映射的有界集为有界集，因此由F的连续性可得序列{F(xk)}和{F(yk)}有界。又由引理10和(19)式可得

(20)

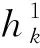
(21)

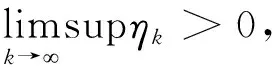
(22)

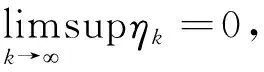
〈F(xkj)-F(xkj-γ-1ηkjrμ(xkj)),rμ(xkj)〉>σ‖rμ(xkj)‖2，

(23)

由假设条件A)和rμ(xk)的连续性，在(23)式中令j→∞有

(24)

4 数值实验

用2个数值实验来测试算法1，工具是R2018a版本的MATLAB和华硕笔记本(CPU：inteli7-4710HQ)。选取10-4作为停机准则，即当‖r(x)‖≤10-4时，程序终止。为了方便描述，把文献[14]的算法2.1记为算法2，把文献[17]的算法3.1.2记为算法3，把文献[18]的算法1记为算法4。其中算法1的参数取为：σ=0.5，γ=0.5，μ=1.6；算法2的参数选取为：σ=0.99，γ=0.4，μ=1；算法3的参数取为：σ=0.5，γ=0.5，μ=1，α=0.1，β=0.02，ω=0.1；算法4的参数取为：σ=0.3，γ=0.5，μ=1.4。

例1考虑n维非单调变分不等式问题

其中，SD={(-1,…,-1)}且S={(x1,…,xn):xi∈(-1,0),∀i}。并且x1→x2在[-1，1]上是拟单调的，可参考文献[20]定理3.1和例3.1，而n≥2时F在C上不是拟单调的。

在例1中，首先通过计算PC(x0)随机生成8个初始点，其中x0是随机生成的向量。然后使用算法1、算法3和算法4分别对初始点不同的例子1分别求解8次。最后，统计例1中算法8次计算后的总迭代次数的平均值iter，总函数值计算次数的平均值nf和总的耗费时间的平均值time(单位：秒)。在表1中报告了数值实验的结果。

表1 例1的数值实验结果

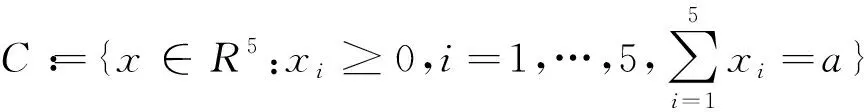
在例2中分别选取不同的初始点，然后对算法1、算法2和算法4进行测试，将三者的数值实验结果进行比较。在表2中报告了数值实验的结果。

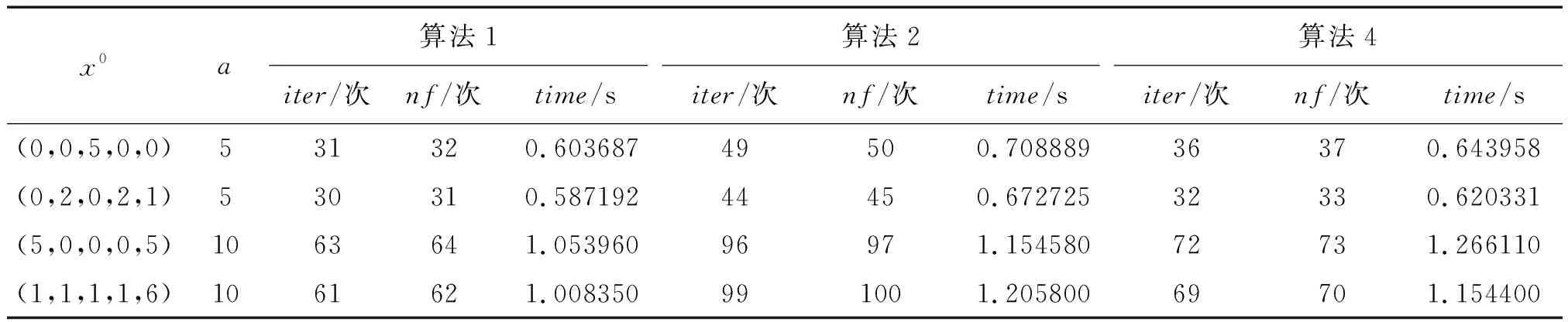
表2 例2的数值实验结果

通过表1和表2的数值实验结果可以发现，算法1的迭代次数和运行时间都少于算法2、算法3和算法4，这说明了算法1在一定程度上优于已有算法。