基于恒星敏感器的组合导航技术在极地飞行保障中应用的仿真分析

张强， 吉鹏， 伍瀚宇， 焦浩博， 周睿

(中国民用航空飞行学院空中交通管理学院， 广汉 618300)

远距离跨洋飞行时，极地航线更接近大圆航线，能够显著缩短航程和飞行时间并提高载重，给航空公司带来可观的收益，因此越来越受到航空公司的重视。但是由于极地区域特殊环境和导航设备自身缺陷的双重影响，现阶段的民航机载导航系统针对极地飞行的导航保障能力还存在一定不足[1]。

极地区域陆基导航设施稀少，民航飞机在该区域飞行时主要依靠机载惯导系统(inertial navigation system, INS)/全球卫星导航系统(global navigation satellite system, GNSS)组合导航系统进行导航，手段单一。极地区域磁经差过大，磁场异常，传统的磁罗盘定向方式不再适用；极地区域导航经线迅速收敛，在目前的东北天地理导航坐标系下，惯导力学编排存在计算溢出和方位陀螺施矩困难的问题，这也在一定程度上限制了极地航线的开发；INS自身精度还会随着纬度升高而降低[2-4]；此外，极地区域电磁环境复杂，极光、太阳风暴等都会对GNSS信号造成干扰，导致性能下降。

机载导航设备自身缺陷同样影响极地飞行导航保障。INS虽然自主但存在误差累积的缺点；GNSS受限于自身倾斜轨道，几何精度因子在高纬度区域明显大于中低纬度区域，可接收卫星数量也大大减少，导航性能显著降低[5-7]；此外，GNSS卫星导航系统一旦设备故障或受到人为干扰，其导航定位能力将大大降低甚至失效。如2018年4月美国打击叙利亚期间，该地区全球定位系统(global positioning system，GPS)信号受到多次长时间的严重干扰，导航信号质量非常差甚至中断；2019年7月11日—17日伽利略系统由于位于意大利的地面控制站故障导致瘫痪近一周。

当前，中外不少学者开展了极地飞行导航保障能力提升研究。针对传统坐标系在极地区域不适用这一问题，Maclure[8]提出了格网坐标系导航的概念，Watland[9]提出了一种将地球经纬坐标轴互换的横坐标系方法。文献[10-14]在这两种导航坐标系下研究了组合导航的力学编排和滤波算法。针对GNSS在极地区域工作时性能下降的问题，申功勋[15]、徐卿等[16]研究了利用天文导航系统代替GNSS的相关技术。应用于航空领域的天文导航系统(celestial navigation system, CNS)基于恒星敏感器接收识别恒星等发光星体作为导航源这一技术，可实现大动态条件下的全天时暗弱恒星目标的捕获、跟踪和探测，提供极高精度的姿态信息，且误差不随时间累积。机载CNS性能在军事航空领域已得到了充分验证，如美国RC-135侦察机、B-2轰炸机等均配备了CNS，能显提高组合导航的姿态和位置精度，仅INS/CNS组合就能提供优于20″的姿态精度。2013年哥伦比亚大学成功在南极区域实验其研发的白昼型天文导航系统[17]。

分析前人的相关研究可以发现，利用特殊的导航坐标系能解决惯导力学编排失效的问题，但没有涉及到GNSS存在的缺陷，无法提升机载INS/GNSS导航系统的可靠性；利用CNS代替GNSS组成INS/CNS组合导航系统，理论上避免了GNSS的不足且能全天时输出导航参数，但同时会由于CNS无法输出位置信息而导致定位精度有较大降低。在前人研究基础上，结合极地飞行对导航系统保障能力的实际需求，以及未来民航发展对导航精度的追求，提出将基于恒星敏感器的CNS引入民航，组成机载INS/GNSS/CNS组合导航系统，同时采用格网导航坐标系，以提升民航极地飞行的导航保障能力，通过研究INS/GNSS/CNS在格网坐标系下的滤波算法，并通过仿真校验该组合导航系统在极地区域的性能。

1 格网坐标系与组合导航系统结构

1.1 格网坐标系

典型的格网坐标系如图1所示，过飞机所在位置P点且平行于格林尼治子午面的平面即为格网平面，水平面为切平面，定义格网平面与切平面的交线为格网北向，格网天向同地理坐标系天向重合，格网东向在切平面内且与格网北向垂直构成右手直角坐标系，此即为格网坐标系(G系)。

在格网坐标系下，地理极点仅仅时格网图上普通的位置点，实际使用过程中，将极区航图与格网坐标系相结合，可方便理解相关导航信息。由于各导航子系统的输出信息所参考的坐标系不一致，计算时需要将这些信息转化到同一参考坐标系下。假设P点地理经度、纬度和高度分别为L、λ和h，地理坐标系下真北方向同格网北向的夹角为σ，相对格网坐标系的偏航角、俯仰角和横滚角分别为ψG、θG和γG，则有

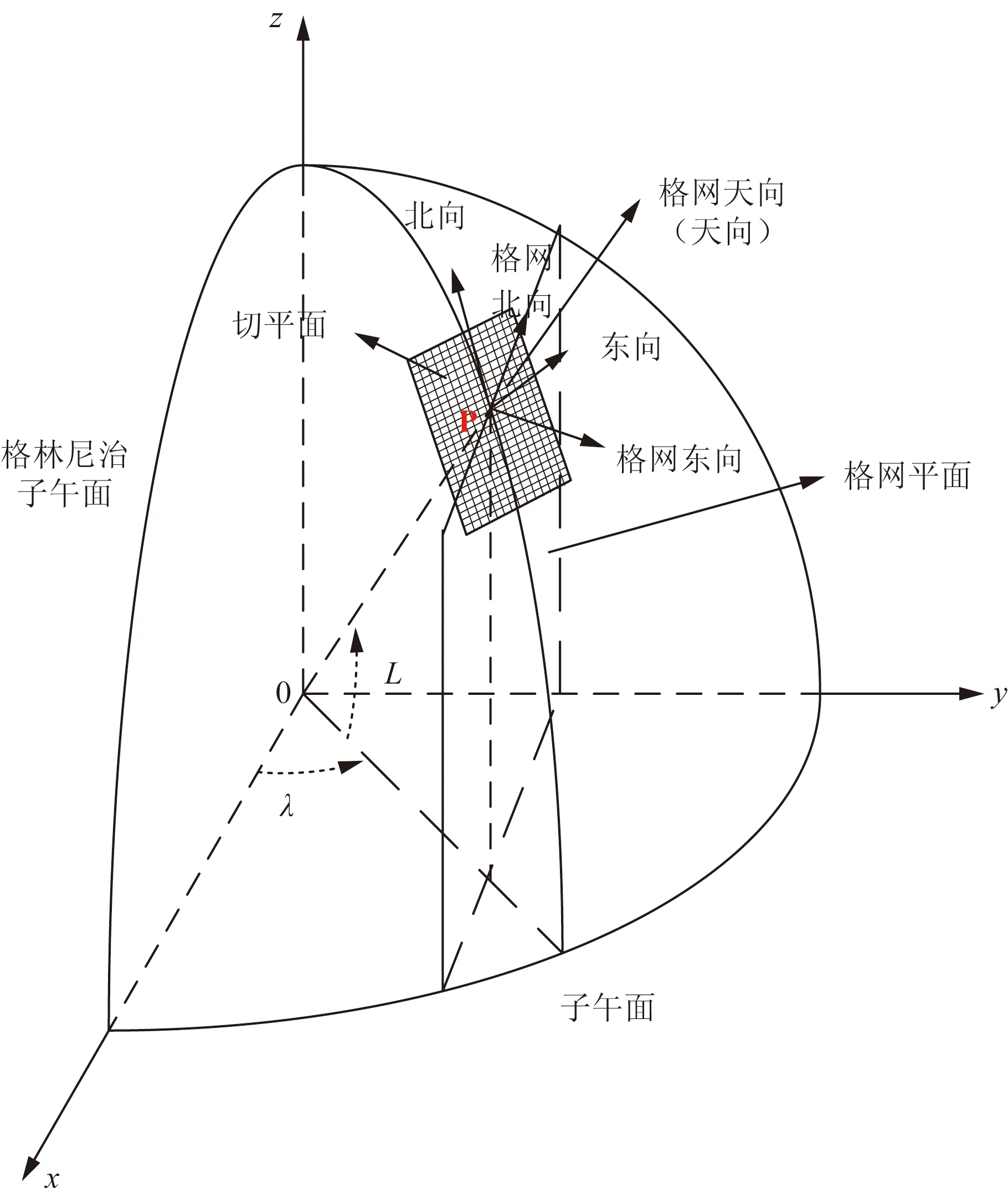
图1 格网坐标系示意图Fig.1 Diagram of grid coordinate system

(1)

同时，东北天地理坐标系n到格网坐标系G的转换矩阵为

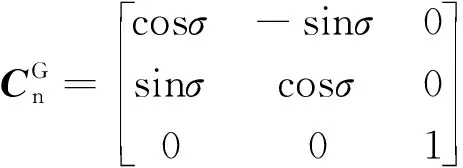
(2)

格网坐标系G到机体坐标系b的转换矩阵为

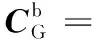
(3)

极地飞行过程中采用方向余弦阵求解位置信息存在较大误差和困难，可用飞机在地心地固坐标系e下的坐标表示其位置信息，格网坐标系到e系的转换矩阵为

(4)

1.2 INS/GNSS/CNS组合导航结构

INS/GNSS/CNS组合导航系统中，INS能输出飞机姿态、速度和位置的全部信息，且更新频率最高；GNSS只有速度和位置信息，更新频率较低；机载CNS只能输出姿态信息，更新频率也较低。因此本组合导航系统仍以INS为主导航系统，GNSS用于修正INS的速度和位置误差，CNS用于修正INS的姿态误差。

多信息源组合导航的结构多种多样，按原理大体可以分为集中式、并行式和序贯式，不同结构对整体系统的精度、容错性和计算量都有不同的影响。理论上，并行式结构如联邦滤波器结构作为一种次优滤波算法，具有最高的容错性，计算量也少，完美契合极地飞行对导航系统的要求，但从实际发展来看，联邦滤波诞生几十年来并未得到广泛的实际应用，不少学者甚至认为该模型结构与集中式相比并无明显优势[18-20]。集中式可得到最高的精度，但容错性较低，子系统发生故障会对整体系统造成明显影响。序贯式兼具集中式和并行式的优点，在两者之间取得了平衡，但其稳定性差。实际上，民航系统对导航系统的稳定性有极高要求，且各导航子系统故障概率都较低，因此采用图2所示的集中式结构进行研究。

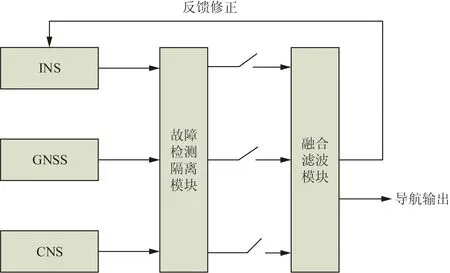
图2 INS/GNSS/CNS组合导航系统结构Fig.2 Structure of integrated navigation system

该模型结构包括故障检测隔离、集中滤波和反馈修正模块。导航子系统通过故障检测算法判断是否正常工作[21]，当导航子系统都正常工作时，采用滤波算法得到最优导航精度，输出结果同时对INS反馈修正；当某一导航子系统如GNSS工作不正常时，通过故障识别将其隔离修复，只将剩下工作正常的子系统INS与CNS的输出信息融合，并将输出结果对INS反馈修正。由于各导航子系统本身故障概率就低，结合故障检测模块，理论上已经满足实际需求。

仅对融合算法部分进行研究，故障检测及隔离在后续工作内容中展开研究，组合导航系统的故障检测原理及相关技术可参考文献[21-24]。

2 组合导航系统滤波算法

2.1 INS/GNSS/CNS组合导航状态方程

在采用的适用于极地飞行导航的格网坐标系下，选取INS/GNSS/CNS组合导航系统的状态向量为

(5)

INS/GNSS/CNS组合导航系统的状态方程为

(6)

2.2 INS/GNSS/CNS组合导航量测方程

飞机在极地区域飞行，当导航子系统全部正常工作时，选取INS和GNSS两者的位置速度之差以及INS和CNS计算得到的姿态的差值作为量测值。

由于GNSS输出的是地心地固坐标系下的导航信息，而惯导状态方程得到的速度信息是基于格网坐标系下的，因此需要将GNSS速度信息转化为在同一导航坐标系下，可表示为

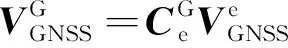
(7)

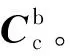
(8)

因此，INS/GNSS/CNS组合导航系统的量测方程为

(9)

(10)

式(10)中：I为单位矩阵。

2.3 INS/GNSS/CNS组合导航信息反馈修正

将惯导系统误差估计值反馈到INS中，对其状态误差进行修正，能得到更精确的导航信息，这对弥补极地飞行过程中INS和GNSS性能下降造成误差增大有重要意义，同时也符合未来民航发展对导航系统精度越来越高的要求。对INS/GNSS/CNS组合导航系统，各子系统输出信息是离散的，反馈修正过程也是周期性的，因此需要将状态方程和量测方程离散化，每次滤波周期结束得到惯导估计误差，INS接收反馈并减去该估计误差，即完成该滤波周期的惯导修正。第k-1～k个滤波周期的组合导航反馈修正只需将上个周期的状态向量归零，即

(11)

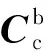
3 组合导航的仿真校验

3.1 仿真条件设置

本仿真通过设置飞机初始状态和飞行状态参数模拟一次穿越极点的极地飞行。根据飞行各时间点的数据以及导航子系统的性能指标，利用轨迹发生器反推得到各导航子系统的导航数据，最后将子系统的导航数据进行融合，分析INS/GNSS/CNS组合导航系统在该极地飞行时的导航保障能力。本次仿真设置的飞行初始状态如表1所示。

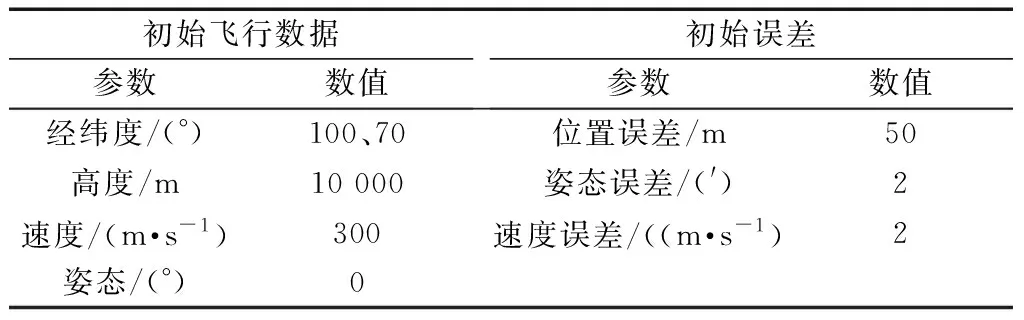
表1 飞行初始状态Table 1 The initial flight state

本次仿真所设置的导航子系统性能参数为：惯导陀螺随机常值漂移0.01°/h，随机游走系数为0.001；惯导加速度计常值偏置100，随机游走系数为0.001；GNSS位置精度20 m，速度精度为1 m/s；CNS姿态测量精度5″。

为了模拟实际极地飞行可能存在的导航系统风险，本次仿真试验设计飞行过程中导航子系统完全正常工作和GNSS发生故障而被检测隔离1H两种情况，以验证INS/GNSS/CNS组合导航系统在极地飞行过程中的导航保障能力。

3.2 仿真结果及分析

本仿真为了更直观显示INS/GNSS/CNS组合导航系统的性能，特设置格网坐标系下的INS/GNSS组合导航系统和INS/CNS组合导航系统作为对照。作为对照的两组合导航系统算法参考前人的研究文献。同时，为了显示简洁，将各组数据进一步处理，以位置误差为例，可表示为

(12)

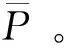
每次仿真总时长为5 h，飞行过程中仅进行小幅度姿态和速度变化，当所有导航子系统均全程正常工作时，各组合导航系统的参考姿态误差和参考位置误差的仿真结果如图3、图4所示，其中误差数值信息如表2所示。

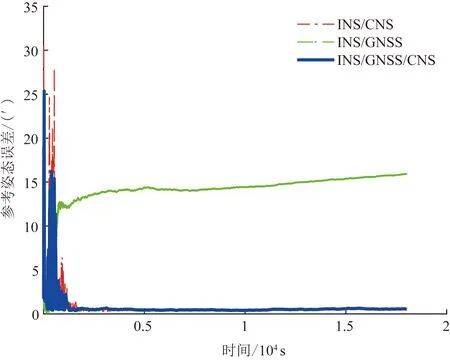
图3 参考姿态误差Fig.3 Error of reference attitude

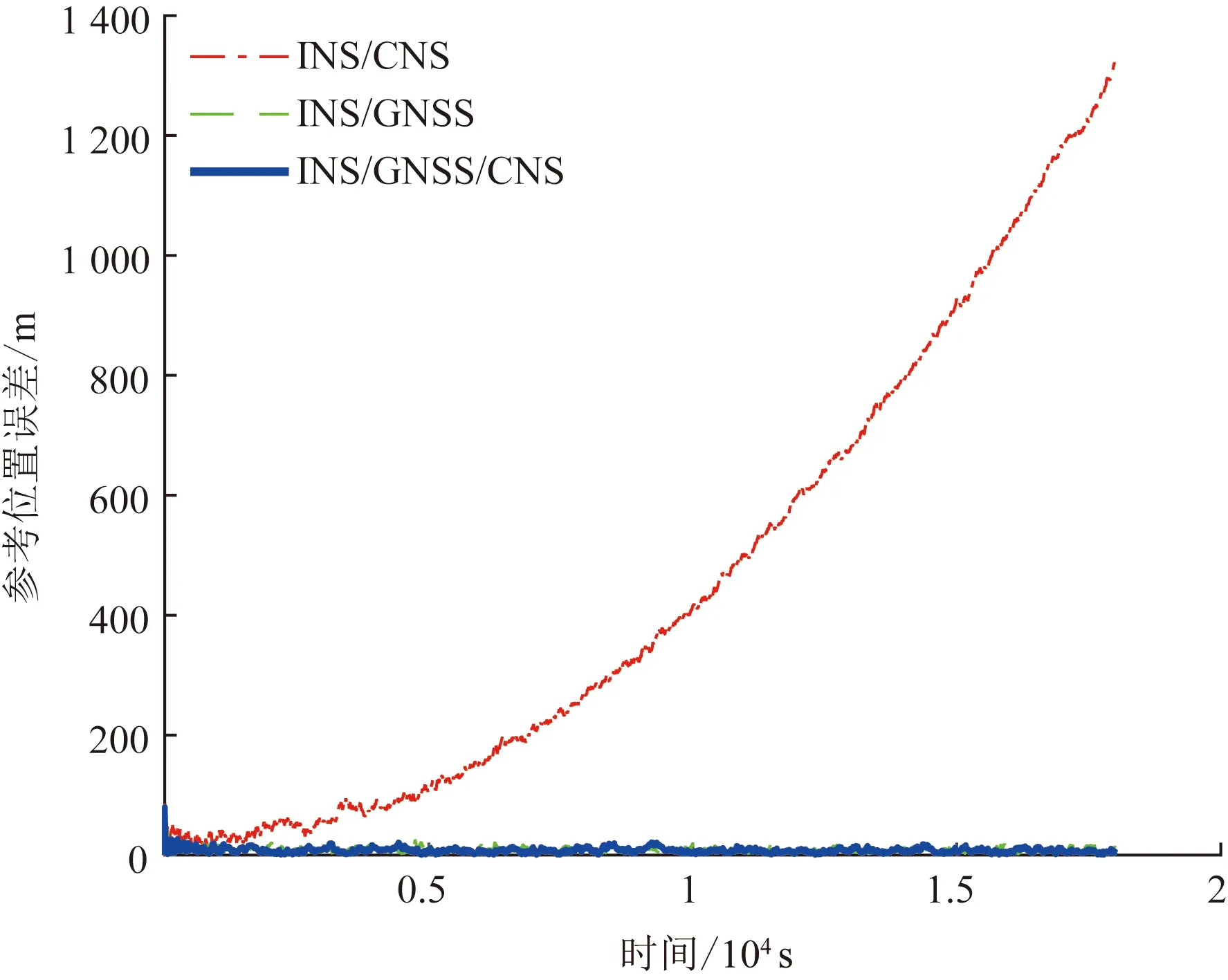
图4 参考位置误差Fig.4 Error of reference position

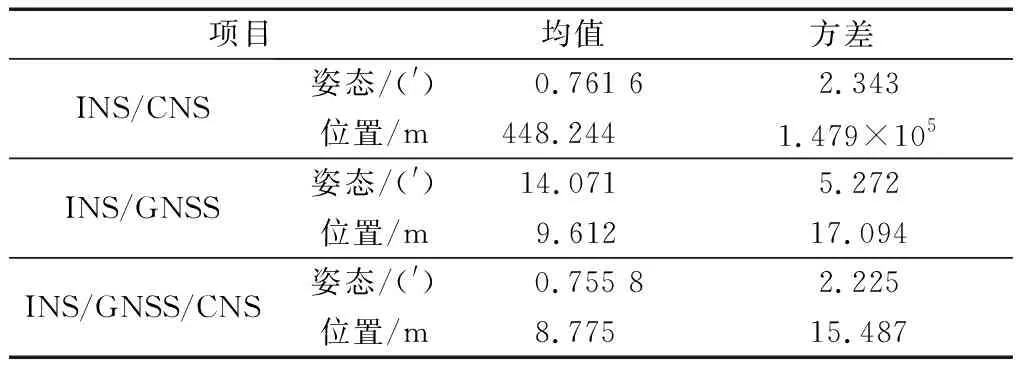
表2 组合导航误差统计值Table 2 Error statistics of integrated navigation systems

从图3、图4可以看出，当导航子系统全部正常工作时，INS/CNS组合导航系统虽然能输出极高的姿态信息，但由于CNS只能输出姿态信息，INS缺乏位置和速度参数的修正，导致整体位置误差呈逐渐增大趋势，精度较差；INS/GNSS组合导航系统虽然能输出精度极高的位置信息，但姿态精度较差；采用的INS/GNSS/CNS同时具备极高精度的姿态和位置信息。从表2可以发现，INS/GNSS/CNS组合导航系统的位置精度相比INS/GNSS还有一定提升，这是由于CNS极高的姿态精度修正了INS的陀螺漂移，提升了组合导航的整体精度。

分析可知，极地飞行过程中导航子系统还是存在一定的故障风险的，并不能保证飞行全程都能保持正常工作。当飞行过程中某一子系统如GNSS出现故障时，假设所有3个组合导航系统均能及时发现并隔离故障子系统，本次仿真前4 h为正常工作情况，后1HGNSS发生故障被隔离，仿真结果如图5、图6所示，误差具体数值分析如表3所示。

从图5、图6可以看出，当GNSS发生故障并被隔离后，INS/GNSS组合导航系统相当于只剩INS工作，因此其姿态和位置误差通过累积方式迅速增大，较短时间内就到了极差的地步；而本文提出的INS/GNSS/CNS组合导航系统还能保持极高精度的姿态信息，同时通过对INS陀螺漂移的修正，整体位

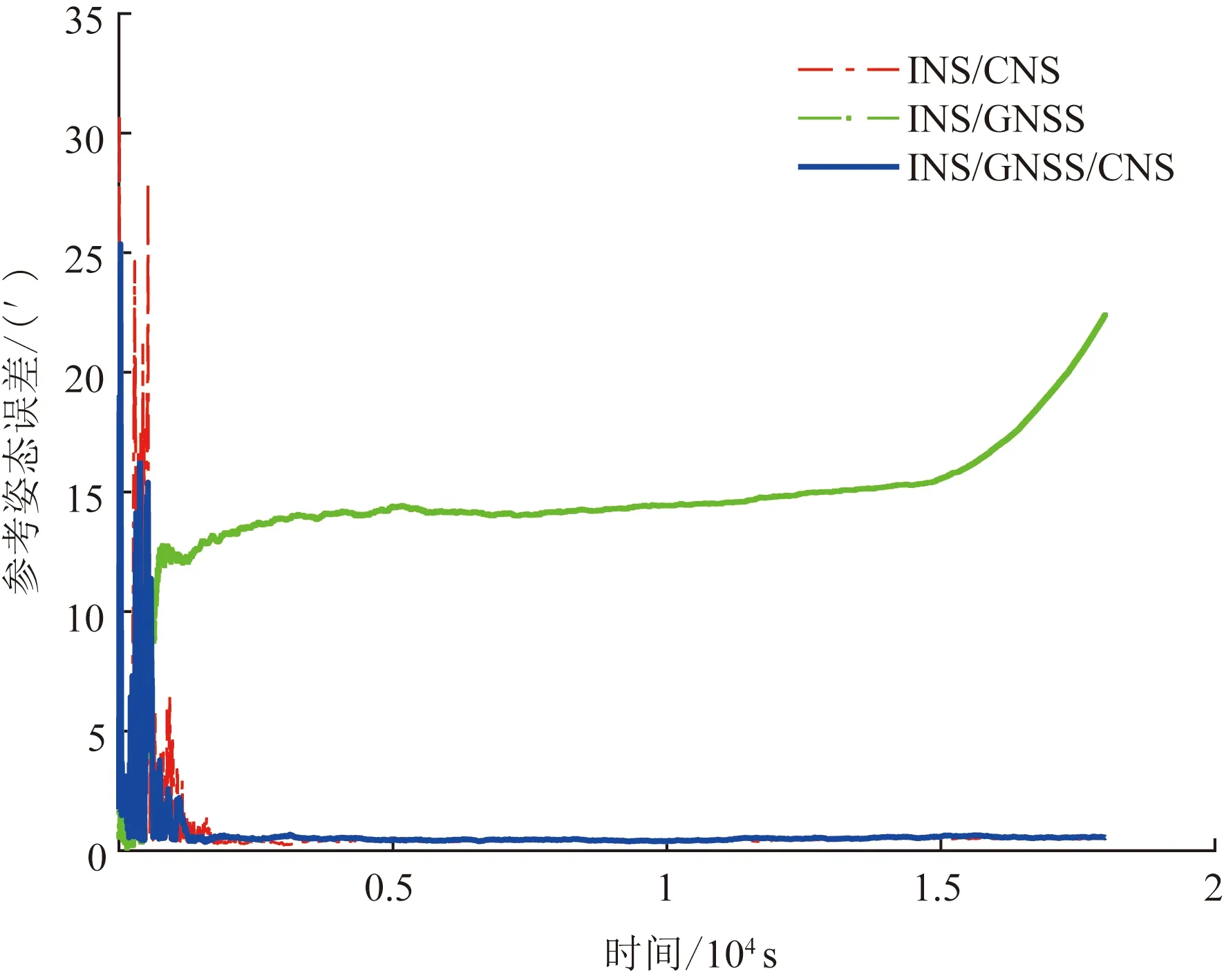
图5 参考姿态误差Fig.5 Error of reference attitude

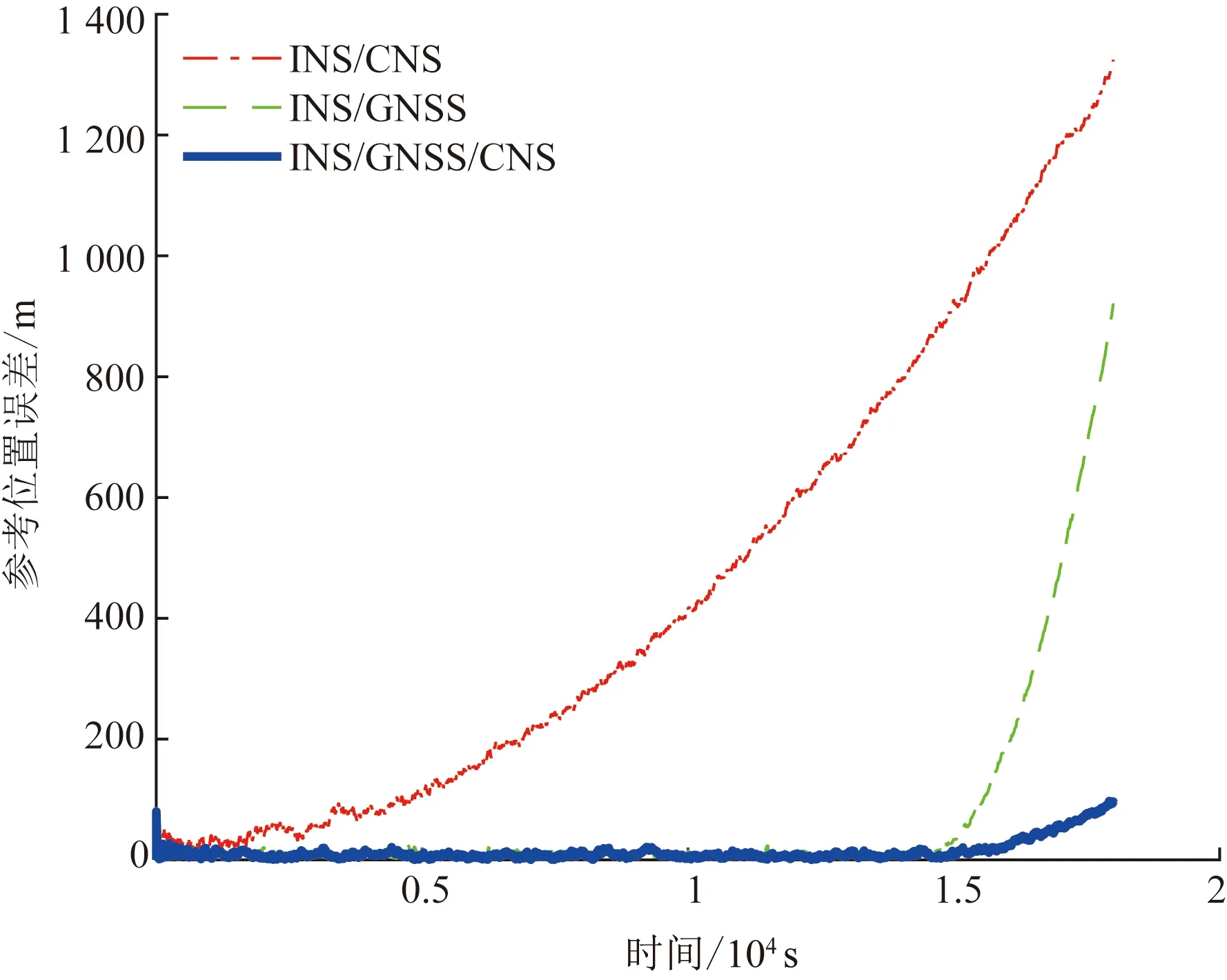
图6 参考位置误差Fig.6 Error of reference position

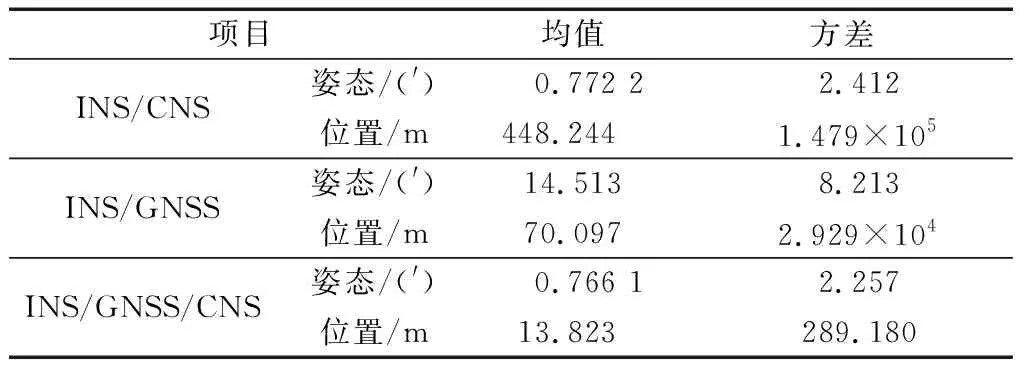
表3 组合导航误差统计值Table 3 Error statistics of integrated navigation systems

置误差增加较缓，1H后位置误差在100 m以内；而INS/CNS组合导航系统无影响。可以发现，在发生导航子系统故障时，INS/GNSS/CNS组合导航系统还能较长时间内提供较好的导航能力保障。

4 结论

通过分析民航极地飞行过程中存在的导航保障能力的不足，综合研究前人针对极地飞行导航系统的研究，提出了采用INS/GNSS/CNS组合导航系统提升极地飞行的导航保障能力。同时，还研究了该组合导航系统的结构以及在格网坐标系下的滤波算法，并通过仿真分析对该系统的极地飞行导航保障能力进行验证。得出如下结论。

(1)采用格网坐标系可解决INS在高纬度的力学编排问题，在该坐标系下，导航系统在飞机穿越极点时仍能正常输出，扩大了极地航线的开辟范围。

(2)当极地飞行过程中各导航子系统均能正常工作时，INS/GNSS/CNS相比前人学者提出的INS/GNSS和INS/CNS组合导航系统，能够同时保证极高精度的姿态、位置等信息，更符合未来民航发展对导航系统性能的需求。

(3)当极地飞行过程中发生导航子系统如GNSS故障时，INS/GNSS/CNS组合导航在较长时间内还能保障飞行导航精度需求。

综上，仿真表明所提出的INS/GNSS/CNS组合导航系统，能显著提升极地飞行的导航保障能力。同时，由于研究水平及条件有限，仅做了简单仿真，未对极地飞行实际环境的各种复杂情况以及组合导航系统在极地的实际应用进行试验。在极地航线发展迅速的背景下，具有进一步深入研究必要与价值。