爆炸消减钢桥面顶板-纵肋焊接残余应力的模拟分析

马斌, 邓扬, 刘涛磊

(北京建筑大学土木与交通工程学院, 北京 100044)

顶板-纵肋焊接连接是正交异性钢桥面板的关键受力构件之一，焊接过程中不均匀的热输入，使焊缝及其邻近区域产生较高的残余拉应力。桥梁服役过程中，在车辆荷载和残余拉应力的共同作用下此处极易产生疲劳裂纹。

目前，中外学者对正交异性钢桥面的残余应力问题进行了大量研究，特别是在考虑不同温度下材料非线性特性的残余应力数值模拟方面取得了较多的研究成果。曹宝雅等[1]应用热-结构耦合数值模拟的方法分析了顶板厚度对顶板与纵肋焊接残余应力的影响规律，结果表明增加顶板厚度会显著增大焊接连接的横向残余应力。李爱群等[2]建立了U肋与横隔板的焊接有限元模型，分析了焊缝附近横隔板、U肋残余应力的分布特征及弧形切口切线方向残余应力分布规律。Lee等[3-4]针对不同形式的焊接连接进行了有限元数值模拟，研究了关键焊接参数对残余应力的影响。Teng等[5]采用有限元数值模拟方法分析了钢板在焊接过程中的残余应力，并讨论了焊接速度、试件尺寸、外部约束条件和有无预热对残余应力的影响。

爆炸法因其能耗低、价廉、不受场地的限制，而被广泛关注[6-7]。管建军等[6]应用流固耦合法模拟了爆炸冲击波与中厚板焊接接头相互作用消减焊接残余应力的过程，模拟结果表明爆炸处理可以较好地消减被炸面双向残余应力。Wu等[8]对800 MPa级高强度钢手工焊接接头进行爆炸处理，试验结果表明爆炸处理不仅可以降低焊接接头表面残余应力还可以降低沿厚度方向的残余应力。Liu等[9]通过试验与数值模拟探究了爆炸法消减对接钢板焊接残余应力的处理效果。Zhang等[10]通过数值模拟与试验研究的方式，揭示了爆炸处理消减焊接残余应力的机理，讨论了药条形状、药条宽度、布置位置及爆炸速度对焊接残余应力消减效果的影响。

现有的爆炸法消减残余应力研究对象多为平板结构，将其用于消减钢桥面焊接残余应力的研究较少。为此，利用有限元软件AYSYS和显式动力分析软件LS-DYNA对爆炸法消减顶板-纵肋焊接残余应力的过程进行了模拟，分析了焊接残余应力分布特征，研究了爆炸法对焊接残余应力的消减效果， 研究成果可为工程实践提供参考。

1 数值模拟基本理论

爆炸法消减顶板-纵肋焊接残余应力的数值模拟分为焊接加热、冷却过程中焊接件收缩变形(产生残余应力)和焊缝区域受炸药爆炸产生的爆轰作用(消减残余应力)两部分。焊接残余应力的产生是三维热弹塑性问题，温度场和应力场相互的非线性作用不明显，故采用间接耦合方法计算焊接过程中应力的变化过程：先进行温度场分析，然后将各时间点的温度场结果作为结构分析的热载荷，得到应力场分析结果。残余应力的消减过程是以焊接残余应力作为预载荷，将隐式分析单元转换为显式分析单元，采用任意拉格朗日-欧拉法(arbitrary Lagrange-Euler algorithm, ALE)耦合算法进行爆炸冲击动力分析。

1.1 焊接模拟基本理论

1.1.1 温度场

焊接过程中，瞬态温度场的热传导微分控制方程为[11]

(1)

式(1)中：k、ρ和Cp分别为材料的热导率、密度和比热容；T为温度；t为时间；QTR为内热源强度；x、y、z为三维坐标；当考虑材料非线性时，k、ρ和C均为温度T的函数。

式(1)的初始条件和边界条件分别为[12]

T(x,y,z,0)=T0(x,y,z)

(2)

(3)

式中：Nx、Ny、Nz为垂直于边界的方向余弦；qs为单位面积上的外部输入热流；hc为对流换热系数；T0为周围介质温度；Tr为辐射热源温度；σ为Stefan-Boltzman常数；ε′为热辐射系数。

1.1.2 应力场

热弹塑性应力场分析基于材料的Von Mises屈服准则及双线性等向强化模型，应力场分析的基本方程如下。

任意单元的平衡方程为[13]

dFe+dRe=Kedδe

(4)

式(4)中：dFe为单元节点上力的增量；dRe为温度引起的单元初应变等效节点力的增量；Ke为单元刚度矩阵；dδe为节点位移增量。

材料的应力-应变本构方程为

dσ=Depdε-CthdT

(5)

Dep=De+Dp

(6)

式中：Dep为整体刚度矩阵；De为弹性刚度矩阵；Dp为塑性刚度矩阵；Cth为热刚度矩阵；dσ为应力增量；dε为应变增量；dT为温度增量。

任意单元的几何方程为

dεe=Bdδe

(7)

式(7)中：dεe为任意单元应变增量；B为应变增量矩阵；dδe为单元节点位移增量。

热-结构弹塑性应力有限元分析具体求解过程为：在焊接温度场结果算出后，逐步加载温度增量，计算各节点位移增量[13]，将式(7)代入式(5)材料应力-应变本构方程，可得任意单元的应力增量dσ。根据上述分析流程就可得到焊接过程最终的残余应力分布状态[14]。

1.2 爆炸处理基本理论

爆炸是非线性连续介质力学问题，具有多介质、大变形以及高度非线性等特点，物理现象极为复杂[15]。非线性连续介质力学计算方法中，按其采用的坐标系可分为Lagrange法、Euler法和ALE法等。Lagrange法将计算网格固定在物体上，网格跟随物体一起运动和变形，网格点与物体点之间无迁移运动，可简化控制方程的求解过程，准确的描述不同材料的应力变化过程。但对于大变形问题，由于网格跟随物体一起运动，物体的扭曲会导致网格的畸变，使计算精度下降，甚至计算失败。Euler法中，网格固定在空间中，网格不随物体的运动而移动，因此网格的计算精度并不会受物体扭曲的影响。但Euler法在描述运动界面时，需采用极为复杂的数学映射对界面进行追踪和处理，进而会产生较大的误差。ALE法将以上两种方法有机结合，充分吸收两者的优势，克服两者的缺点，网格可以在空间中以任意形式运动，即可以独立于物体坐标系和空间坐标系运动[16]。通过规定合适的网格运动形式可以准确地描述物体运动界面，并保持网格的合理形状。因此ALE法对爆炸这种大变形问题的数值模拟具有广泛的适用性和实用价值。

使用LS-DYNA进行爆炸冲击载荷下的结构响应计算时，利用非线性连续介质力学的方法以及高斯定理，推导出ALE法描述的控制方程如下[16]。

质量守恒方程(连续性方程)：

(8)

动量守恒方程(平衡方程)：

(9)

能量守恒方程：

(10)

式中：wi为网格迁移速度；vi为运动速度；xi为空间位置；xj为空间位置；σji为柯西应力；fi为单位质量的体积力；e为质量比内能；Qi为热通量。

2 实例分析

2.1 有限元模型

以某悬索桥钢桥面板为研究对象，该桥顶板厚度16 mm，纵肋上口宽300 mm、下口宽170 mm、高280 mm、厚度10 mm、间距0.3 m。考虑正交异性板桥梁的结构对称性，首先建立了基于有限元软件ANSYS的顶板-纵肋半结构足尺有限元模型，然后建立了基于显式动力分析软件LS-DYNA的顶板-纵肋焊接模型、炸药、空气的流固耦合有限元模型。材料采用Q345钢，钢材不同温度条件下的热物理性能及力学参数取值参加文献[17-18]，顶板-纵肋焊接模型尺寸如图1所示。焊接过程的温度场分析选取六面体八节点热单元Solid70，应力场分析选取隐式结构单元Solid185，爆炸过程选取显式六面体单元Solid164。

纵肋与顶板间焊接采用部分熔透焊缝，坡口宽度8 mm，焊脚尺寸8 mm，长度200 mm，焊缝单元长度2 mm。在焊缝附近区域进行网格加密处理，尺寸控制在2 mm，在远离焊缝区域选取较大网格尺寸，尺寸控制在4 mm。模型共计119 500个单元，138 168个节点。设顶板-纵肋有限元模型坐标系方向：顶板-纵肋截面宽度方向为x方向，顶板-纵肋截面高度方向为y方向，顶板-纵肋结构沿焊缝方向为z方向，坐标系原点位置如图1所示。顶板和纵肋结构对称面施加对称约束，顶板左侧约束y、z向位移，顶板右侧约束y向位移，顶板-纵肋焊接有限元模型如图2所示。

在顶板-纵肋隐式有限元模型基础上，基于有限元软件LS-DYNA建立炸药及空气模型，采用单面布药的方式将炸药布置在焊缝处，爆炸处理模型示意图如图3(a)所示。炸药截面长度6 mm，炸药截面宽度4 mm，炸药条长度200 mm，空气域尺寸300 mm(x轴)×300 mm(y轴)×200 mm(z轴，炸药条长度方向)，网格尺寸4～6 mm，满足计算精度[19]，空气域6个外表面假设为无反射边界条件。炸药与空气共节点连接，采用欧拉网格进行网格划分，顶板-纵肋焊接模型采用拉格朗日网格进行网格划分，欧拉网格与拉格朗日网格之间的流固耦合建模使用*Constrained-Lagrange-in-Solid命令进行描述[19]，爆炸处理有限元模型如图3(b)所示。

图1 分析模型尺寸Fig.1 Dimensions of analysis model

图3 爆炸处理模型Fig.3 Model of explosion treatment

2.2 材料参数设置

LS-DYNA中的多材料任意拉格朗日-欧拉公式(multi-material arbitrary lagrange-euler method，MM-ALE)及流固耦合算法(fluid-solid interaction，FSI)可以有效模拟爆炸处理的过程，炸药在空气中爆炸包括3个阶段：①爆轰；②爆轰波在空气介质中传播；③爆轰波、顶板-纵肋焊接模型及空气介质之间的相互作用[20]。由于爆炸处理的瞬时和高能量特性，为准确得到爆炸处理后焊接残余应力分布情况，炸药爆轰产物、空气及钢板的本构关系分别使用JWL(Jones-Wilkins-Lee)状态方程、等γ物态方程、Johnson-Cook方程进行描述[6]。

2.2.1 钢板

在进行爆炸处理的有限元分析时，钢板的动态应力-应变方程为Johnson-Cook本构模型，该模型能够准确地描述大应变、高应变率和高温度下的力学行为[21]。

钢板屈服应力σy可描述为

σy=(A+Bhardenεpn)(1+clnε*)(1-T*m)

(11)

(12)

式中：εp为等效塑性应变；ε*为等效塑性应变率；A为初始屈服应力；Bharden为硬化常数；C为硬化指数；n为应变率常数；m为热软化指数；Tmelt为熔化温度；Troom为环境温度。

2.2.2 炸药和空气

炸药假设为TNT橡胶炸药，密度1.601 g/cm3，爆速0.693 cm/μs，查普曼-朱格压力18.5 GPa。炸药及爆轰产物的材料模型用关键字为*Mat-High-Explosive-Burn的高能炸药模型进行描述，炸药爆炸的能量释放采用JWL状态方程进行描述，该状态方程将爆轰压力定义为爆轰产物的相对体积与爆炸初始内能的函数[21]。

JWL状态方程为

(13)

式(13)中：Peos为爆轰压力；V为爆轰产物的相对体积；e为单位体积内能；E0为单位体积初始内能；A、Bharden、R0、R2、ω为使用炸药的材料参数，A=5.409 GPa、B=0.094 GPa、R1=4.5、R2=1.1和ω=0.35。

空气用理想气体材料模型*Mat-Null描述，密度取1.29×10-3g/cm3。空气介质的密度和内能直接影响在炸药与顶板-纵肋焊接模型之间传播的爆轰波强度，空气选用多线性多项式状态方程(*Eos-Linear-Polynomial)描述内能与压力之间的关系[21]。

空气介质的状态方程为

P=C0+C1μ+C2μ2+C3μ3+

(C4+C5μ+C6μ2)e

(14)

(15)

式中：P为空气中的爆轰压力；ρ0为初始密度；μ为密度的比率；C0、C1、C2、C3、C4、C5和C6为多项式系数。

因空气假定为理想气体，式(14)可通过设C0=C1=C2=C3=C6=0，C4=C5=γ-1进一步简化，其中γ为空气比热容比，γ=1.4[22]。一种理想气体的压力可表示为

(16)

式(16)中：ρ和e均为与温度相关的量。

3 残余应力分析

对焊接-爆炸处理的数值模拟进行分析，以图2中顶板-纵肋焊接有限元模型为基础进行焊接过程的模拟，以图3中添加了炸药及空气单元的爆炸处理有限元模型为基础进行爆炸处理的模拟，以此对钢桥面残余应力的产生与消减过程进行分析。

3.1 焊接残余应力模拟

顶板-纵肋焊接温度场有限元分析过程中，周围环境温度20 ℃，结构外表面施加对流换热边界条件，对流系数20 W/(m2·℃)[23]。焊缝金属的填充过程使用生死单元技术进行模拟，焊接过程开始前，将焊缝单元“杀死”；焊接过程中，依次将“杀死”的单元“复活”，同时对复活的单元加载热源模拟焊缝金属的填充及热源加热过程[1]。

焊接移动热源的计算公式为

HGEN=(ηUI)/(Avdt)

(17)

式(17)中：HGEN为生热率，W/m3；热效率η=0.7；焊接电压U=28 V；焊接电流I=280 A；A为焊缝截面积,mm2；焊接速度v=10 mm/s；dt为各焊缝单元长度的焊接时间。

数值模拟时，先进行焊接温度场模拟，模拟从0开始，焊接热源移动速度10 mm/s，时间步长0.2 s，第21 s焊接结束的同时开始冷却过程，第2 441 s冷却结束。顶板-纵肋焊接及冷却过程的温度场变化云图如图4所示，整个焊接及冷却过程温度动态变化清晰可见。焊接热源移动的初始时刻，温度场升温迅速且不稳定，在热源移动一段时间后，焊接模型上形成准稳态温度场，此时温度场以固定形态随热源一起移动。焊接进行中、焊接结束及焊接冷却结束的温度分布情况如图4所示，可以看出，最高温度接近1 683 ℃。第2 441 s时温度云图温差在1 ℃以内，认为顶板-纵肋焊接模型冷却至室温，冷却过程结束。

图4 焊接温度场变化过程Fig.4 Changing process of temperature field of welding

以焊接温度场分析为基础，将温度场计算结果加载在顶板-纵肋焊接模型上进行应力场分析，温度场与应力场分析的时间步保持一致[24]。随着热源移动，焊缝金属不断填充，模型温度上升，金属膨胀受周围金属的约束作用使金属产生塑性变形[13]。应力场分析中横向残余应力方向为x轴方向，纵向残余应力方向为y轴方向。焊接及冷却过程的纵向残余应力变化云图如图5所示，焊接进行中、焊接结束及焊接冷却结束的应力分布情况如图5所示。图5(a)中灰色部分为焊接进行中未激活填充的焊缝金属，此时最大纵向残余应力为280 MPa。图5(b)为第21 s焊接过程结束时纵向残余应力的分布情况，此时最大纵向残余应力为256 MPa。应力场计算最后一个冷却步的计算结果即为焊接残余应力，顶板-纵肋焊接模型的残余应力分布如图5(c)所示，纵向残余应力最大为264 MPa。

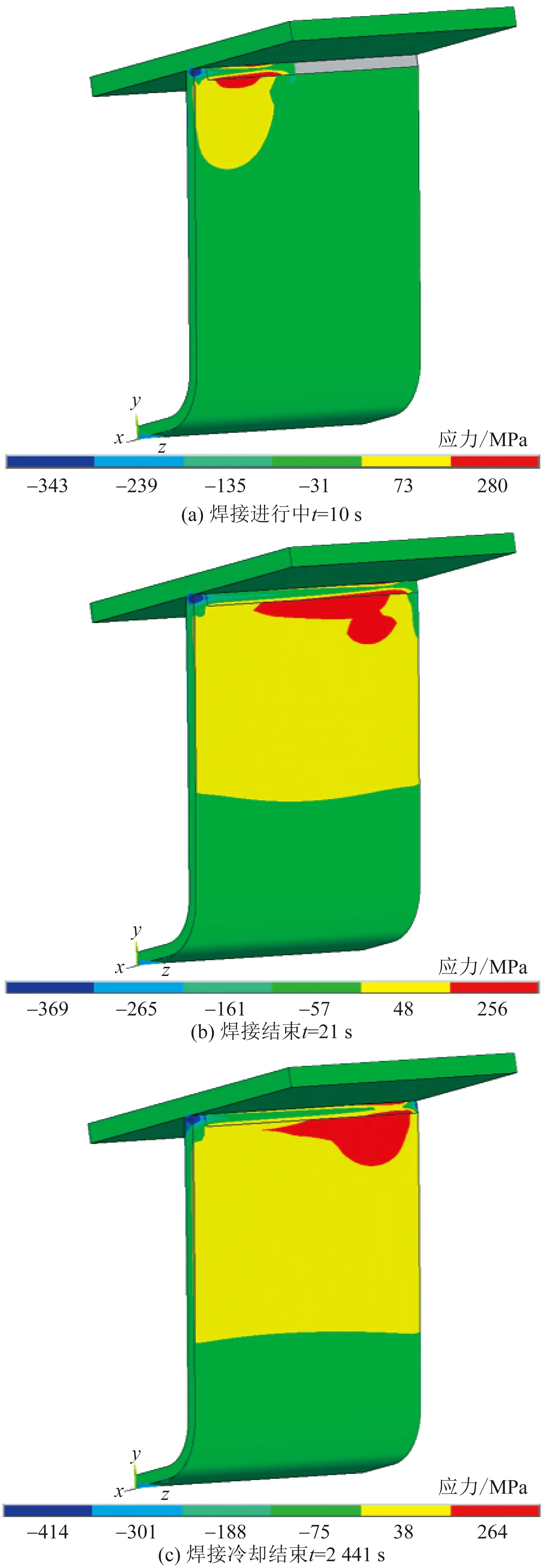
图5 焊接应力场变化过程Fig.5 Changing process of stress field of welding

研究表明，顶板-纵肋焊接连接极易在焊趾处产生疲劳裂纹，且裂纹形态为顶板贯穿型，即裂纹从焊趾处开始萌生，沿焊缝长度和顶板深度发展，引起顶板贯穿断裂[25]。焊接残余应力沿顶板宽度方向(坐标系x轴方向，图1)分布如图6所示。图6(a)中，顶板横向残余应力主要分布于焊缝及其邻近区域，离焊缝越近，残余应力值越大。横向残余应力在下表面处横向残余应力值最大。图6(b)中，顶板纵向残余应力主要分布于焊缝及其邻近区域，纵向残余应力值从上表面到下表面逐渐增大，纵向残余应力在下表面处纵向残余应力值最大。横纵向残余应力主要分布于下表面处。

图6 顶板宽度方向残余应力分布Fig.6 Residual stress distribution in width direction of deck

3.2 爆炸处理残余应力模拟

在顶板-纵肋焊接残余应力场的基础上，进行爆炸处理的数值模拟分析，采用*Initial-Detonation命令引爆布置于焊缝处的炸药。第100 μs炸药爆炸产生的爆轰波趋于平缓，认为爆炸处理过程结束。爆炸处理过程中的残余应力场变化云图如图7所示，整个爆炸处理过程中应力动态变化清晰可见。炸药爆炸进行中、炸药爆炸结束及爆炸处理结束的纵向残余应力分布情况如图7所示，爆炸处理结束后，图中纵向残余应力最大为169 MPa，焊接残余应力场得到明显消减和均化。

图7 爆炸处理应力场变化过程Fig.7 Changing process of stress field of explosion

焊趾及焊根处残余应力在炸药爆炸处理过程中随时间变化的时程曲线如图8所示，可以看出，焊趾及焊根处焊接残余应力在爆轰波未到达之前为拉伸残余应力。爆轰波波前存在极高的局部压缩应力，传播到此处后，使此处残余应力值的大小和方向产生明显变化[7]。爆轰波在焊接结构表面发生多次折射和反射，使此处拉伸残余应力与压缩残余应力相互转化[7]。波前通过后，应力值振动的振幅和频率逐渐减小趋于稳定，焊接过程中因不均匀的热输入产生的塑性应力得到明显消减。

焊缝长度方向(坐标系z轴方向，图1)爆炸处理前和处理后焊趾及焊根横纵向残余应力对比如图9所示，可以看出，顶板-纵肋焊接过程结束后，焊趾及焊根处存在较大的拉伸残余应力，此处横纵向残余应力曲线走势相似，中间段走势接近水平，且焊缝首末段20 mm内走势较陡。实际桥梁中，纵肋长度约为3 m，远大于20 mm，故可忽略焊缝首末两端残余应力走势，取中间段的残余应力进行分析。中间横截面处焊趾、焊根横向残余应力分别为112 MPa和96.9 MPa，纵向残余应力分别为117 MPa和196 MPa。炸药爆炸处理后，各点处残余应力值发生变化，残余应力峰值减小，超过屈服强度的塑性残余应力得到明显消减。焊趾、焊根处的横向残余应力分别剩余-46.9 MPa和-163 MPa，消减降幅分别达到159 MPa和260 MPa；纵向残余应力分别剩余约-161 MPa和28.3 MPa，消减降幅分别达到278 MPa和167.7 MPa。爆炸处理工艺较为彻底的消减了焊接残余应力，模拟结果与工程应用实例接近[6]。

图8 爆炸时残余应力时程曲线Fig.8 Residual stress time history curves during explosion treatment

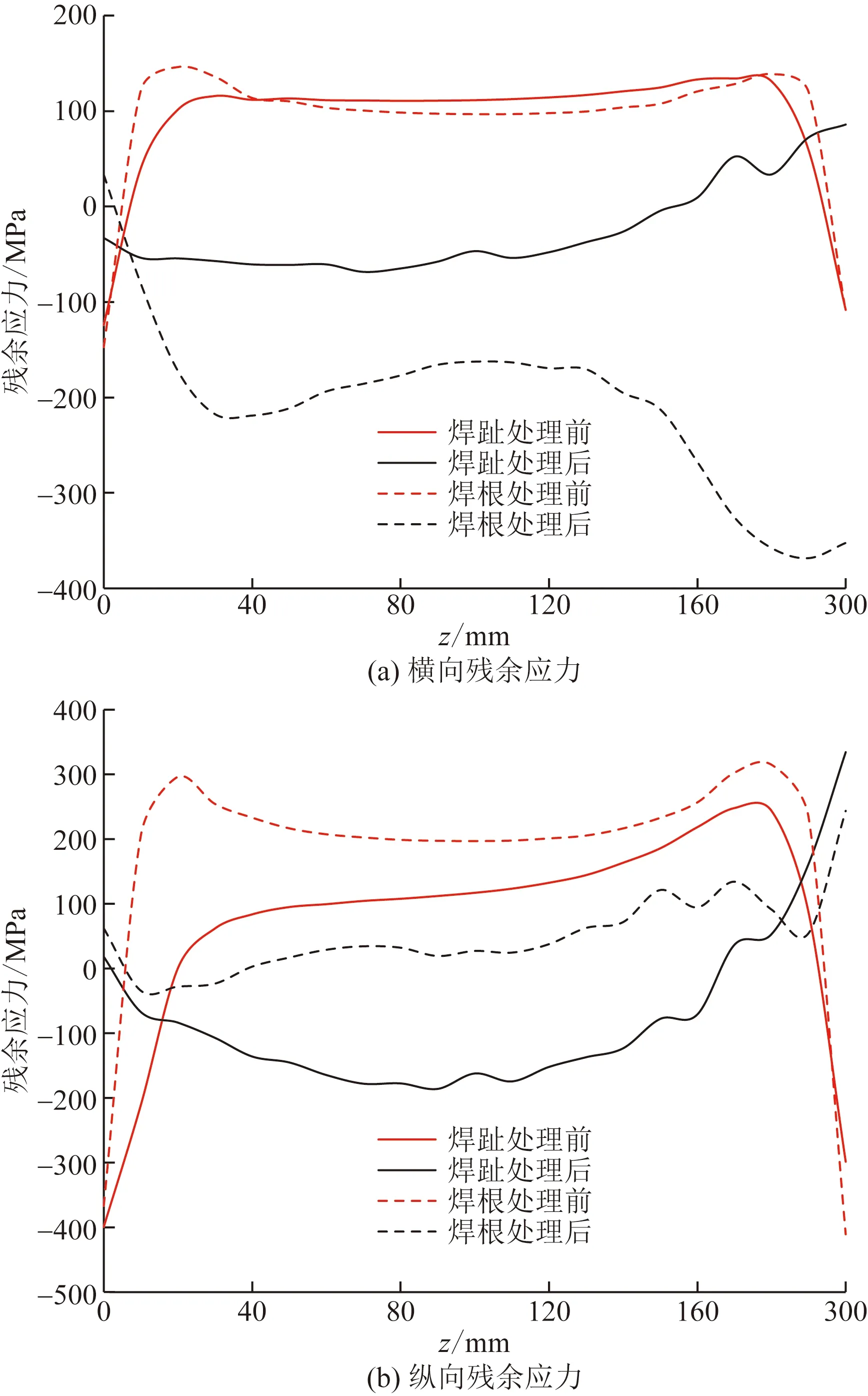
图9 焊缝长度方向残余应力分布Fig.9 Residual stress distribution in length direction of weld

4 结论

对正交异性钢桥面顶板-纵肋焊接连接焊接残余应力的产生过程和爆炸处理后的消减过程进行了有限元数值模拟，分析了焊接及爆炸处理后残余应力分布规律，得出如下结论。

(1)焊接过程在焊缝及其邻近区域产生较大的残余拉应力，焊趾处横向残余应力高达112 MPa，纵向残余应力高达117 MPa，此处存在较高水平的残余应力是引起顶板极易产生疲劳裂纹的重要原因。

(2)爆炸处理后，焊趾处横向残余应力消减降幅达159 MPa，纵向残余应力消减降幅达278 MPa，爆轰波在顶板-纵肋焊接连接内传播并在自由边界发生多次折射和反射，使焊接残余应力重新分配，消减了焊接残余应力。

(3)爆炸处理消减顶板-纵肋焊接残余应力的数值模拟实现了焊接、爆轰及爆轰波与焊接模型间相互作用的多个物理过程，具有广泛的工程实例参考价值。