变压器用片式散热器传热结构改进的数值分析
戚美, 路成, 陈庆光, 刘磊, 陈文毅
(山东科技大学机械电子工程学院, 青岛 266590)
片式散热器是油浸式变压器广泛选用的冷却装置,片式散热器具有成本低、结构简单、散热效率高的优点,其换热性能直接影响变压器内部绕组等金属器件的使用寿命。因此提高片式散热器的换热性能对降低成本和延长变压器使用寿命具有重大意义。为了提高片式散热器的换热性能,中外学者进行了大量研究。殷浩洋等[1]通过数值计算研究了片式散热器防腐涂层的导热率对片式散热器散热能力的影响,研究得出提高防腐涂层的导热率可以实现在减小风机速率的同时或减少散热片个数的同时保证散热效果,有利于实现变压器的节能和小型化设计。Kim等[2]通过改变风机的位置和个数,对散热器外部流动的冷却空气的流畅进行分析,得出当油流量为44.4 L/min时,最高可将换热性能提高22%。Shokouhmand等[3]在片式散热器各片流量分布不均匀的情况下,研究片数对散热器换热性能的影响,得出增加片数更有利于提高片式散热器的换热性能。徐天光等[4]采用数值模拟研究与试验验证相结合的方法,对自然油循环、强迫油循环两种条件下散热器的散热性能进行研究,得出自然循环下,相对于自冷散热,风机冷却的散热效果较强,并且随着油流量的增加散热性能增强。王宏建等[5]通过数值模拟研究了具有收缩式角孔通道结构的片式换热器流量分布特性和流动均匀性,利用相对标准差对其流动均匀性进行评价,得出与传统片式散热器相比,入口设置收缩式角孔通道后,散热器的流量相对标准差更低,流量分布更均匀,更有利于换热。
综上所述,目前中外学者对于片式散热器的研究主要集中在壁面涂层、提供风机冷却、改变流量分布等方面,而对外部辅助传热结构的研究较少。为此,提出在片式散热器两侧安装散热板,并在散热板上设置穿孔,辅助散热器传热,通过数值模拟的方法研究散热板、穿孔直径对片式散热器对流换热、辐射换热和综合换热性能的影响。旨在提高片式散热器的换热性能,达到节能环保、降低能耗的目的,可为片式散热器的设计和优化提供参考。
1 片式散热器结构模型及工作原理
1.1 结构模型
以3片散热片构成的散热器为研究对象,每片散热片厚度为10 mm,间距为45 mm,对应模型Ⅰ。首先在散热器Y方向两侧安装散热板,对应模型Ⅱ;然后在散热板设置孔径为16、18、20、22、24 mm的穿孔,分别对应模型Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ,分析穿孔直径对散热板换热性能的影响。以设置16 mm穿孔散热板的模型Ⅲ为例,其几何模型如图1所示。片式散热器的几何尺寸如表1[6]所示。

图1 片式散热器的三维模型Fig.1 Three-dimensional model of panel-type radiator
为准确模拟片式散热器外部的换热环境,在片式散热器外部X、Y、Z方向,创建长度分别为1 100 mm×2 480 mm×4 480 mm的空气域,如图2所示。
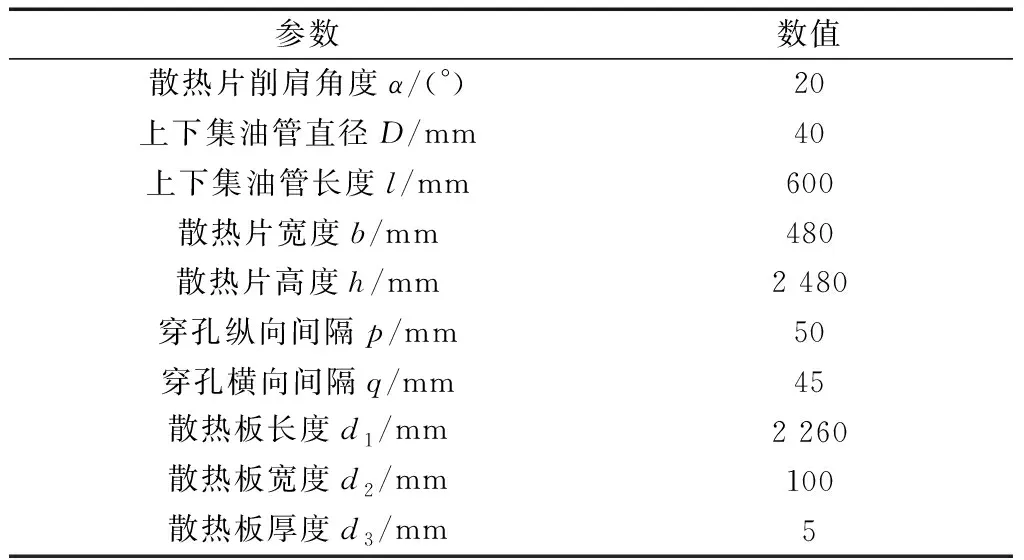
表1 片式散热器的主要几何尺寸[6]Table 1 Main geometric dimensions of panel-type radiator[6]

图2 设置空气流域后的模型Fig.2 Model after setting the air flow domain
1.2 工作原理
变压器在工作过程中会产生大量的热量,油浸式变压器的冷却介质为变压器油,变压器油在吸收热量后,温度升高,密度减小,与温度较低的变压器油产生密度差,在浮升力的作用下向油箱顶部的上集油管流动。变压器油由上集油管进入片式散热器后,将热量传递给各散热片壁面,散热片壁面通过对流及辐射换热来降低壁温,从而降低散热片内的油温,冷却后的变压器油经下集油管流出进入变压器油箱冷却变压器内绕组等部件[7-8]。
2 数值模拟理论
2.1 网格划分
对片式散热器几何模型进行非结构网格划分,网格总数为8.9×106。网格无关性验证结果表明,当网格数大于8.5×106时,网格数对模拟结果的影响可忽略不计,网格如图3所示。

图3 部分网格示意图Fig.3 Configuration of a partial computational mesh
2.2 边界条件
片式散热器上集油管管口设置为速度入口,取入口流速为0.03 m/s,温度为353 K。片式散热器下集油管管口设置为压力出口。变压器油的物性参数采用随温度T变化的拟合关系式,各物性参数的拟合关系式如表2所示[9]。

表2 变压器油的物性参数[9]Table 2 Physical parameters of transformer oil[9]
外部空气域Z轴负方向设置为压力进口,Z轴正方向设置为压力出口。将空气密度形式设定为基于涡黏假设,设定其体积变化系数,理想气体的体积变化系数等于其绝对温度的倒数,即为1/293 K-1,其余壁面设置为无滑移条件[10]。片式散热器壁面材料为冷轧钢板,壁厚为1 mm,导热热阻较小,故壁厚对于研究结果的影响可以忽略不计,将片式散热器模型的壁厚默认设置为0,只考虑热对流和热辐射的影响,不考虑散热器壁的热传导。
2.3 辐射模型选择
片式散热器各片之间距离较近,散热单片之间存在热辐射影响,故在进行换热分析时,考虑辐射换热是必要的。FLUENT中提供了P1、Rossland、DTRM、S2S、DO共5种辐射计算模型,其中DO模型适用于灰体、非灰体、漫反射、镜面反射以及半透明等各种介质的辐射,并且适用于所有光学深度(不透明度)范围的辐射换热问题。本次数值模拟中空气介质参与辐射,光学深度为0,故选用DO辐射模型。
2.4 湍流模型选择
散热器表面与外界空气属于自然对流传热,由于片式散热器长宽比过大,可视为“垂直壁面自然对流”。格拉晓夫数Gr为浮升力/黏滞力比值的一种度量,在自然对流中的作用与雷诺数Re在强制对流中的作用相当,为无量纲数,Gr的计算公式为
(1)
式(1)中:g为重力加速度,取9.81 N/m2;αv为体积变化系数,对于理想气体等于绝对温度的倒数,取1/293 K-1;ΔT为散热器壁面与空气的温差,取40 K;l为特征长度,取2 260 mm;ν为运动黏度,取1.6×10-5m2/s。
Gr评判标准参考如表3[11]所示,经计算,外部空气流域的Gr为6.03×1010,流动状态为湍流。

表3 流态判断依据[11]Table 3 Judgment basis for flow status[11]
近年来,k-ε(k为湍动能,ε为耗散率)湍流模型广泛用于各种形式的流动与传热[12-14],并且计算过程稳定,易于收敛,故选取k-ε湍流模型。开启标准k-ε湍流模型后,在k-ε湍流模型的下设选项中选择enhanced wall treatment和full buoyancy effects选项,强调壁温影响和浮升力作用。
3 模拟分析
3.1 散热板对于片式散热器换热性能的影响
图4为油温随下集油管出口距离的变化图,变压器油在下集油管中继续冷却,距离出口越远,油温越稳定。可以看出,模型Ⅰ中,距离出口0.3 m处油温为333.57 K,模型Ⅱ中,距离出口0.3 m处油温为326.66 K,降低了6.91 K。
图5为两种散热器中散热片、散热板的散热量分布图。可以看出,两种模型中散热量差距在于两侧安装的散热板,其散热量分别为96.64 W和94.15 W。
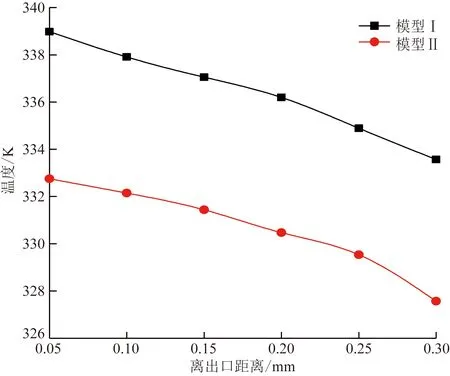
图4 油温随出口距离的变化Fig.4 Variation of oil temperature with outlet distance
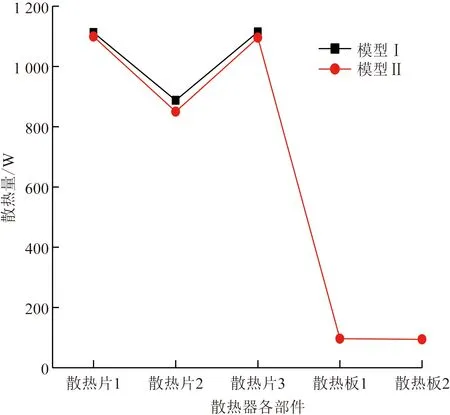
图5 散热器各部件的散热量分布Fig.5 Distribution of heat dissipation of each component of radiators
将图5中各部件的散热量累加,模型Ⅰ的总散热量为3 114.18 W,模型Ⅱ的总散热量为3 235.2 W,模型Ⅱ比模型Ⅰ的总散热量高出3.9%。
3.2 穿孔散热板综合换热性能的影响
在散热板表面设置孔径为16、18、20、22、24 mm的穿孔,在安装两侧散热板基础上,分析穿孔直径对散热板综合换热性能的影响。
3.2.1 散热板辐射换热性能分析
辐射换热是物体之间相互辐射和吸收的综合作用,散热器的辐射和吸收在表面上进行,物体表面热阻的变化会引起辐射换热量的变化,辐射换热量是影响散热器辐射换热的重要因素。散热器表面热阻Rl的计算公式为
(2)
式中:Rl为散热片表面热阻,(m2·K)/W;ε′为固体表面发射率;A为散热面积,m2。
表4为两侧散热板A′、B′的辐射散热量分布,模型Ⅱ两侧散热板A′、B′的辐射散热量最高,分别为32.59 W和32.64 W。穿孔直径增大,散热面积减小,散热板表面热阻增大,辐射散热量减小。

表4 散热板的辐射散热量Table 4 Radiation heat dissipation of heat plates
采用未穿孔散热板与各穿孔散热板辐射换热量的比值Qr/Qr0对散热板的辐射换热性能进行评价分析,其中Qr0和Qr分别为两侧散热板穿孔前和穿孔后的辐射换热量。如图6所示,随着穿孔直径增大,Qr减小,Qr/Qr0减小。由式(2)可得,穿孔直径增大,散热面积减小,表面热阻增大,导致散热板表面与外部环境间的辐射换热量减少,进而影响散热板的辐射换热性能。模型Ⅶ中24 mm穿孔的散热板的Qr/Qr0比值最小,其两侧散热板A′、B′的Qr/Qr0分别为0.800 9和0.816 2,相比辐射换热性能最佳的模型Ⅱ,其分别降低19.91%和18.38%。

图6 不同穿孔直径下Qr/Qr0的变化Fig.6 Variation of Qr/Qr0 with different perforation diameter
3.2.2 散热板对流换热性能分析
在对流换热中,努塞尔数Nu是指流体层流底层的热导阻力与对流传热阻力之比,表示对流换热强烈程度的准数,为无量纲数,Nu的计算公式为
(3)
式(3)中:L为传热面的几何特征长度,m;h为流体的表面对流换热系数,W/(m2·K);k为导热系数,W/(m·K)。
图7为两侧散热板A′、B′的努塞尔数变化。可以看出,穿孔直径增大,两侧散热板的Nu增大,孔径为24 mm时两侧散热板的Nu最大,分别提高至345.43和343.26。
采用未穿孔散热板与各穿孔散热板努塞尔数的比值Nu/Nu0对散热板的对流换热性能进行评价分析,其中Nu0和Nu分别为两侧散热板穿孔前和穿孔后的努塞尔数。如图8所示,随穿孔直径增大,Nu/Nu0降低。这是因为穿孔的存在会扰动散热板表面的流场,穿孔直径越大,扰动越强烈,局部对流换热效果越好,进而影响整个散热板表面的对流换热性能。模型Ⅶ中穿孔直径24 mm散热板的换热性能最佳,其散热板A′、B′的Nu/Nu0为1.276 8和1.293 3,相比模型Ⅱ中未穿孔的散热板,散热板A′、B′的对流换热性能分别提高27.68%和29.33%。
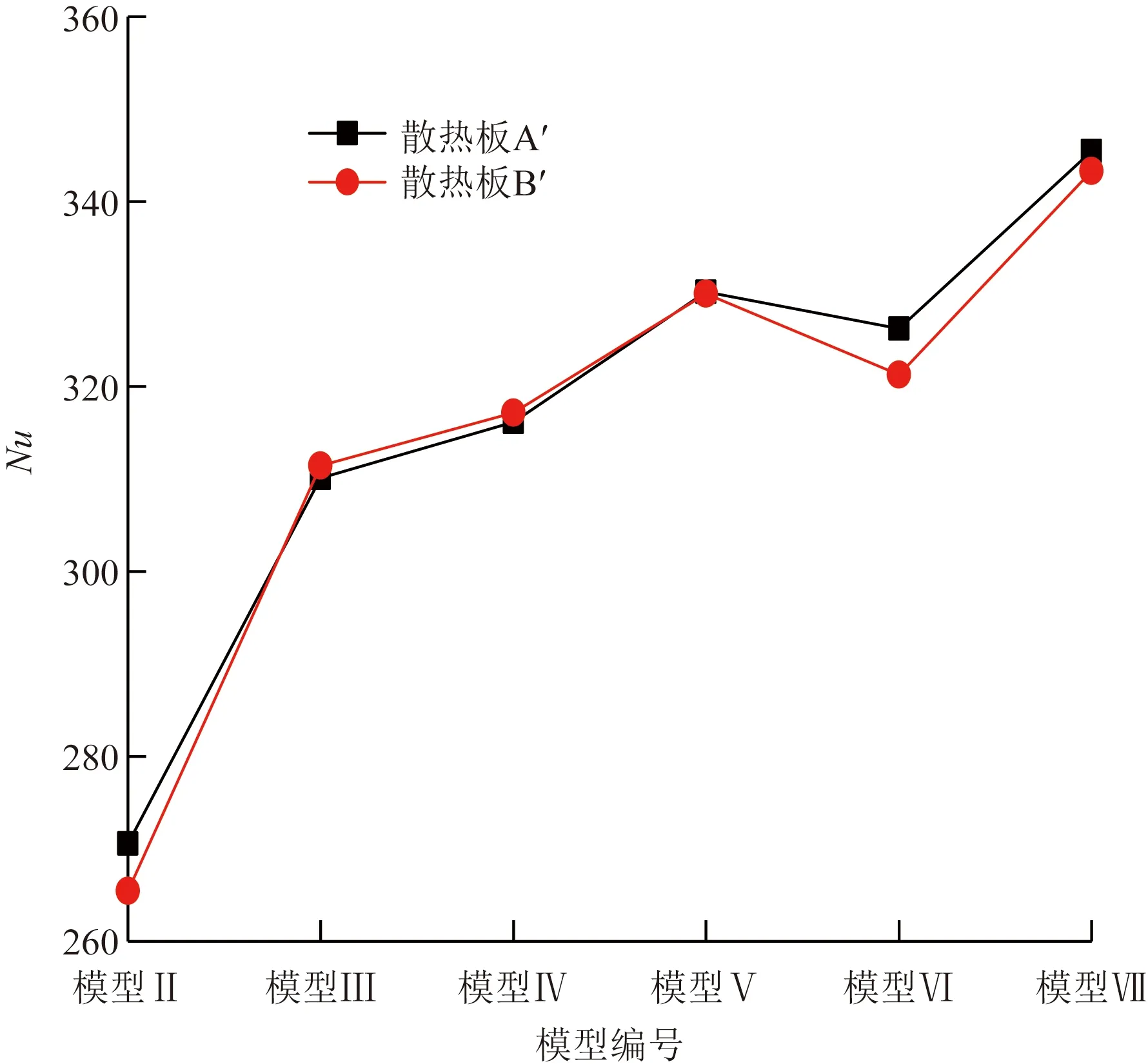
图7 不同穿孔直径下Nu的变化Fig.7 Variation of Nu with different perforation diameter
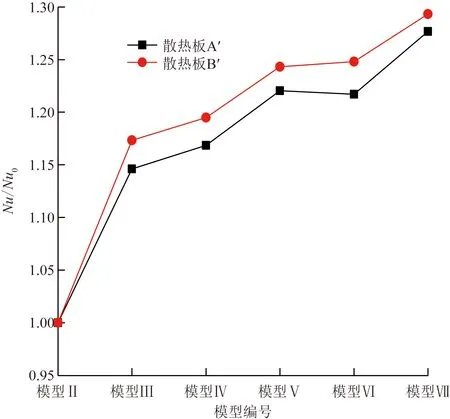
图8 不同穿孔直径下Nu/Nu0的变化Fig.8 Variation of Nu/Nu0 with different perforation diameter
3.2.3 散热板综合换热性能分析
3)结构思考力是期刊高级管理人员的必备技能。美国著名的管理学学者罗伯特·卡茨曾指出,高效的管理人员应当具备技术性技能、人际性技能和概念性技能等3种技能。结构思考力是概念性技能中最重要的技能,有助于高级管理人员对遇到的难题进行全方位、多维度的分析判断并制订对策方案,从而推动工作的高效开展。
图9为各模型下集油管内油温随出口距离变化。可以看出,模型Ⅳ距离出口0.3 m处的油温最低,为323.79 K。
表5为两侧散热板的总散热量分布表。可以看出,随穿孔直径增大,总散热量没有一直增大或减小,模型Ⅳ两侧散热板的散热量最高,分别为121.24 W和121.23 W。这是因为穿孔直径越大,辐射换热减弱,对流换热增强,总散热量是辐射换热和对流换热综合作用的结果。
因为总散热量是辐射换热和对流换热综合作用的结果,采用未穿孔散热板与各穿孔散热板总散热量的比值Q/Q0对散热板换热性能进行评价分析,其中Q0和Q分别为两侧散热板穿孔前和穿孔后的总散热量。如图10所示,随穿孔直径增大,两侧散热板A′、B′的Q/Q0没有一直增大或减小。这是因为对于散热板本身,总散热量不只受到单一方面的影响,对流换热和辐射换热均对其产生重要影响。模型Ⅳ中穿孔直径18 mm散热板的综合换热性能最佳,其两侧散热板的Q/Q0分别为1.254 6和1.287 6,相比模型Ⅱ中未穿孔的散热板,散热板A′、B′的综合换热性能分别提高25.46%和28.76%。
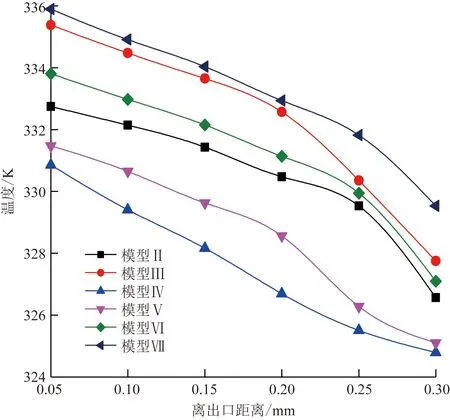
图9 油温随出口距离的变化Fig.9 Variation of oil temperature with outlet distance

表5 散热板的总散热量Table 5 Total heat dissipation of heat plates
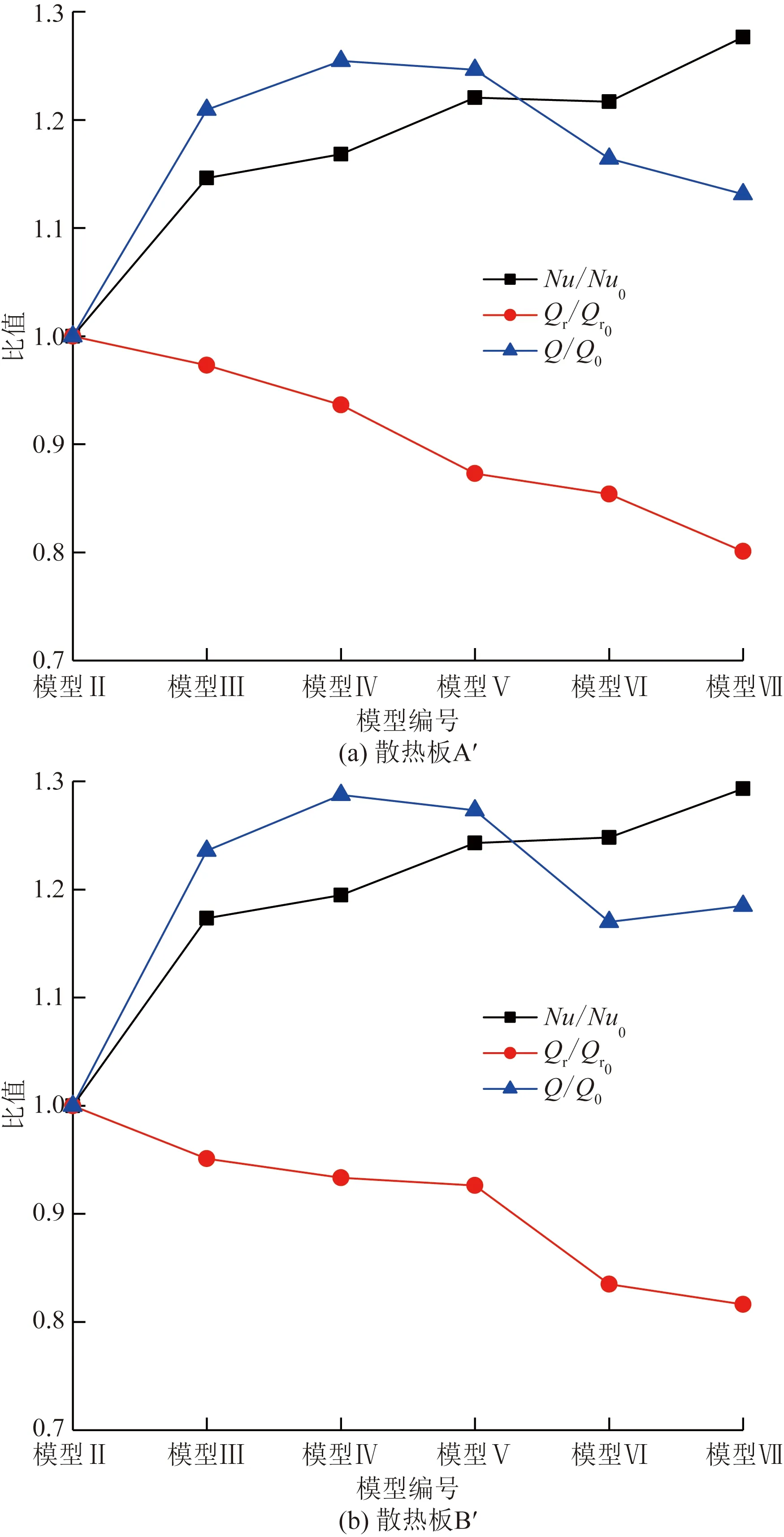
图10 不同穿孔直径下各比值的变化Fig.10 Variation of ratios under different perforation diameter
4 结论
通过数值模拟,分析了穿孔直径对两侧散热板综合换热性能的影响,得出如下主要结论。
(1)安装散热板后,散热器的总散热量提高了3.9%,距离出口0.3 m处油温降低了6.91 K。
(3)穿孔直径增大,散热板A′、B′的辐射换热性能降低,未穿孔散热板辐射换热性能最佳。24 mm穿孔散热板的辐射换热性能最差,相比辐射换热性能最佳的模型Ⅱ,分别降低19.91%和18.38%。
(4)18 mm穿孔散热板的综合换热性能最佳,相比未穿孔的散热板,散热板A′、B′的综合换热性能分别提高25.46%和28.76%,散热器距离出口0.3 m处的油温为323.79 K,选择18 mm穿孔散热板对片式散热器进行安装和改进最佳。

