桥梁退化模型及养护时机研究综述

张洪， 左勤， 辛景舟， 周建庭*

(1.省部共建山区桥梁及隧道工程国家重点实验室， 重庆 400074； 2.重庆交通大学土木工程学院， 重庆 400074)

当前，中国桥梁事业发展迅速，公路桥梁数量已达87.83×104座，里程达6 063.46×104m[1-2]，居世界第一，在取得巨大建设成就的同时，管养压力接踵而至，管养并重时代已经来临，厘清桥梁结构的性能退化机理、开展科学养护，对于保障桥梁安全与路网畅通意义重大。

交通运输部在2020年提出《交通运输部关于进一步提升公路桥梁安全耐久水平的意见》，文件提出着力提升公路桥梁管养水平的意见，指出工作目标：到2035年，公路桥梁建设养护管理水平进入世界前列，公路桥梁结构健康监测系统全面建立，安全风险防控体系基本完善，创新发展水平明显提高，标准化、智能化水平全面提升，平均服役寿命明显延长，基本实现并不断完善管理体系和管理能力现代化[3]。中国重建轻养的观念将逐渐转变为建养并重，目前在桥梁的养护上，还较缺乏科学合理的养护指导，养护措施、养护时机决策较主观化，造成了经济资源的浪费。为科学合理地制定桥梁养护策略，不仅要准确把握桥梁结构性能的退化规律，还要在满足桥梁运营安全适用的条件下兼顾养护成本的经济性，做出最优养护时机决策。为此，以桥梁的退化预测模型、养护时机为研究对象，梳理了退化预测物理模型、数据驱动模型的优劣性，综述了目前确立桥梁最优养护时机方法的研究进展，对该领域发展方向进行讨论，为桥梁管理养护决策工作提供参考。

1 桥梁退化预测模型

中外学者对桥梁结构性能退化开展了大量研究，退化预测方法大致可分为两类，一类是基于退化机理方法，模拟影响桥梁结构退化各种因素的时变情况，建立钢筋锈蚀、混凝土碳化、氯离子渗透等长期劣化、损伤因素与结构承载力、刚度等性能参数间的定量关联模型，即物理模型，进而对桥梁结构性能退化趋势进行预测；另一类方法是数据驱动方法，通过历史统计数据来预测结构的状态。历史统计数据主要是桥梁检测和监测信息，其中蕴含着大量的结构状态信息，现有的大数据分析技术、人工智能算法为检测信息的合理利用提供了科学技术手段[4]，从而有效地预测桥梁退化情况。

1.1 物理模型

物理模型即考虑影响桥梁退化的因素，从桥梁结构构件退化机理角度模拟退化，其基于材料的物理性能演化来分析特定类型的劣化过程。该方法可对某一特定的桥梁和构件进行定量的退化预测，其预测结果精度较高。

在钢筋锈蚀方面，Biondini等[5]针对受侵蚀扩散攻击的钢筋混凝土建立了钢筋锈蚀退化模型，该模型考虑了混凝土无损伤和钢筋均匀腐蚀。Imperatore等[6]研究了锈蚀作用下钢筋的力学行为，并考虑了均匀腐蚀和坑蚀的影响，建立了主要力学性能的衰减方程。周建庭等[7]、辛景舟等[8]从材料层次和构件层次综述了既有锈蚀钢筋力学性能退化模型和黏结性能退化模型，指出了钢筋锈蚀的退化模型的普适性有待提升。

在混凝土碳化方面，通常认为混凝土的碳化深度服从Fick第一定律，碳化深度正比于碳化时间的1/2次方[9-11]，碳化模型不同主要在于碳化系数不同，而碳化系数则与环境条件、混凝土材料相关。张扬等[12]通过快速碳化实验研究了粉煤灰混凝土碳化问题，分析了水胶比、水泥用量和粉煤灰掺量这三个指标对碳化深度的影响。加速碳化实验往往与实际服役情况不符，牛荻涛等[13]采用压榨法逐层测试了混凝土圆柱体试样孔溶液pH，并根据测试结果确定了自然暴露环境下混凝土部分碳化区长度。

在氯离子侵蚀方面，通常认为氯离子扩散规律符合Fick第二定律，在此基础上，杜修力等[14]、Tran等[15]、Wang[16]研究了不同荷载对氯离子扩散特效的影响，建立了不同荷载下混凝土氯离子侵蚀模型。在桥梁构件方面，Cui等[17]提出了一种新的钢筋混凝土桥梁下部结构受氯离子腐蚀时的腐蚀速率模型，该腐蚀速率模型考虑了混凝土开裂后腐蚀速率的加速，适用于典型的海洋环境。江辉等[18]研究了氯离子侵蚀对近海大型桥梁损伤概率的时变影响规律，建立非线性数值模型并开展增量动力分析，获得主塔等构件及桥梁系统的时变易损性曲线。

以上均为基于单一因素的退化模型，实际工程中，桥梁结构或构件退化往往由于多种因素共同作用，对于多因素影响方面，Lu等[19]对现有的斜拉桥拉索腐蚀模型进行了修正，其考虑了应力水平和腐蚀过程的耦合效应，建立了不同服役期的拉索腐蚀深度模型。牛荻涛等[20]通过盐溶液浸泡与碳化交替方式，研究了碳化作用对混凝土中氯离子扩散的影响，但没有对碳化和氯离子扩散共同作用下混凝土劣化做定量考量。Chindaprasirt等[21]用二氧化碳气体腐蚀溶液将混凝土碳化处理，通过实验分析了碳化与氯离子作用下混凝土中氯离子的渗透情况，但这与二氧化碳气体腐蚀特征不符。受实验条件限制，既有多因素影响通常先模拟一个因素引起的退化，在此基础上再模拟另一个因素引起的退化，只是对多重劣化因素简单叠加，没有考虑各因素同一时间上的耦合效应。

1.2 数据驱动模型

1.2.1 回归模型

回归模型假定桥梁退化过程的趋势是确定的，通过大量的历史统计数据分析待预测量的影响因素，建立待预测量与某一变量或多个变量的经验关系，如桥梁技术状况评分与桥龄的关系，该模型避免了复杂的力学演化机理分析，其精确度主要依赖数据的数量和准确性。

回归模型一般可分为线性回归和非线性回归，Shahin[22]提出了一种单因素线性回归公式，以桥龄作为自变量，桥梁技术状况作为因变量，但实际中桥梁技术状况往往与交通量、气候等因素都有关系，因此单因素线性回归难以模拟实际桥梁的退化情况，且在长期预测中缺乏可靠性，Shahin等[22]还提出了一种多因素线性回归公式，以桥龄、桥梁类型作为自变量，但线性回归误差较大，对于桥梁长期性能的预测还缺乏一定的精度。非线性回归模型中，周方[23]通过非线性回归模型预测了预应力混凝土梁桥的技术状况，并通过对比分析验证了采用高斯方程和三角函数的预测模型检验结果较为理想。何天涛等[24]采用负指数作为回归分析模型，将桥龄作为唯一变量，既充分考虑了荷载对桥梁的作用，也考虑了桥型、养护水平等因素对桥梁缺损状况的影响，并用该模型预测了某桥五年的桥梁技术状况评分，结果表明该模型具有较高精度。

以上方法均是基于单一桥梁，回归模型同样适用于区域路网的多座桥梁的退化分析，Goyal等[25]提出了基于比例风险回归的方法，利用某地区的桥梁数据库识别了影响桥梁退化的最关键因素，并量化了退化因素对桥梁条件评级的影响。曹明兰等[26]认为影响多座混凝土桥梁结构劣化的因素很多，致使其劣化模型变化大、类型多，提出了n段线性劣化模型与非线性劣化模型，可用来模拟任意情形的桥梁劣化模式，该劣化模型通过可靠度来反映退化情况，计算过程较为复杂，桥梁技术状况往往更加简单。单爱成[27]利用某一高速路段内所有桥梁的技术状况数据，通过时间—空间转换法延长数据的时间序列，利用负指数函数拟合桥梁技术状况回归曲线，建立桥梁技术状况的退化模型，通过对标准误差、残差平方和、校正决定系数分析，表明该模型优越性较好。其利用时间序列下的20 m等跨预应力简支空心板梁桥技术状况数据做负指数函数回归分析，回归方程见式(1)，回归曲线如图1[27]所示。

Dr=95.911 8{1-exp[-(24.281 0/t)0.457 5]}

(1)

式(1)中：t为桥龄；Dr为桥梁技术状况评分。

为了科学评价回归模型的预测能力，Lu等[28]提出了一种基于数据拟合优度的回归模型预测能力评价方法，并用国家桥梁数据库建立的桥梁构件退化回归模型进行了验证，为建立预测模型评价标准提供了基础。

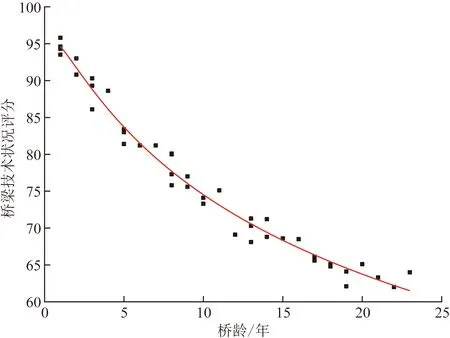
图1 负指数函数回归曲线[27]Fig.1 Negative exponential function regression curve[27]

1.2.2 随机模型

随机模型将桥梁的退化过程看作是一个或多个随机变量(即时间、桥梁构件的状态)，从而可以捕捉到退化过程的不确定性和随机性。随机模型可以分为基于状态的模型和基于时间的模型。在基于状态的模型中，退化过程是通过在离散时间间隔内从一个条件状态转换到另一个条件状态的概率来建模的。在基于时间的模型中，桥梁单元在特定条件状态下的持续时间被建模为随机变量，使用概率分布，如威布尔分布、泊松分布等来描述退化过程。

随机模型中，马尔可夫链应用广泛，张阳等[29]考虑到桥梁各阶段性能退化速率不同，采用多阶段的马尔可夫链，建立了桥梁技术状况退化模型，并预测了某13年桥龄的混凝土空心板桥3年后的技术状况。卢新等[30]开发了基于有限Markov链与Poisson分布建立了桥梁性能退化预测模型，并编写了算法进行运用。Mašovic等[31]提出了一种改进的随机模型，在条件状态下应用Weibull分布来计算停留时间的半马尔可夫桥梁退化模型，该模型在桥梁管理中的适用性较好。马尔可夫模型中重要的一点是确定最优转移概率矩阵，为了实时更新转移概率，郑瑶辰等[32]引入动态贝叶斯理论，利用结构实时的新信息修正时变参数的概率密度函数，更新转移概率矩阵，对结构的性能退化进行准确预测。Mašovic等[33]提出了基于期望最大算法的马尔可夫退化预测模型，将期望最大算法用于计算转移概率，结果表明该算法具有较好的鲁棒性。Wellalage等[34]提出了一种基于Metropolis-Hasting算法的马尔可夫链蒙特卡罗仿真算法，对铁路桥梁构件基于状态的马尔可夫退化模型进行修正，分析表明该方法在路网级桥梁退化预测中预测精度高于基于非线性优化的马尔可夫转移概率矩阵算法预测方法。

此外，灰色理论在桥梁退化预测中也有应用，灰色理论可通过较少数据对桥梁状态进行预测，杨文博等[35]基于灰色理论对某桥进行GM(1, 1)建模，并对建模数据进行相对误差、关联度、均方差比值、小误差概率的检验。灰色模型对于长期预测以及数据波动大的预测精度较低，修正的灰色模型可避免此缺点，刘历波等[36]提出一种基于灰色理论模型并用马尔可夫链修正的灰色-马尔可夫预测模型，结合桥梁数据应用，结果表明该方法比灰色GM(1, 1)预测模型精度、稳定性更高。

1.2.3 人工智能模型

随着计算机科学的发展，人工智能技术已广泛应用到桥梁领域，桥梁退化预测也不例外。人工智能模型包括：人工神经网络、基于案例的推理、期望最大化算法、专家系统等。

在神经网络方面，Allah等[37]构建了逻辑回归、决策树等机器学习算法以及具有实体嵌入的深层神经网络的预测模型，并用于预测桥梁状态。Ali 等[38]提出了一个神经网络模型来研究密苏里州大跨桥梁的上部结构、下部结构和桥面板的退化情况，结果表明该模型能成功预测桥梁未来状况。Li等[39]利用国家桥梁清单数据库建立了桥台的神经网络集成(ensemble neural network, ENN)退化模型，并给出了退化预测曲线，结果表明该ENN模型精度好，但计算成本较大。

在基于案例的推理(case-based reasoning, CBR)方面，Morcous等[40]以加拿大魁北克省259座混凝土桥梁的数据作为一个案例库，提出了用CBR来生成退化模型，该方法考虑了桥梁过去状态对未来的影响，最小化了退化过程中不确定性的影响，但CBR方法存在当案例库数据不足时无法有效建模的缺点。在专家系统方面，Kawamura等[41]根据专家系统评估退化混凝土板的性能，通过神经网络反向传播方法促进对嵌入在系统中的知识库的细化，专家的诊断结果与学习后系统输出的高度一致，验证了该方法的有效性。

上述研究主要针对全桥或者某一构件进行单独预测，未将桥梁及构件数据集成整合。夏烨等[42]对桥梁历史检测信息进行数据集成与规整，将提取的关键参数及数据集进行神经网络训练与验证，生成一系列桥梁构件及结构层的退化模型，其对桥梁结构及构件探索的理论公式为

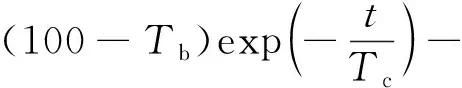
(2)

退化模型关键参数如表1[42]所示。

表1 退化模型关键参数[42]Table 1 Key parameters of the degradation model[42]

综上4种退化预测模型，物理模型从退化机理的角度来模拟桥梁结构或构件退化，可建立较精确的退化预测模型，但是多种退化因素的共同影响导致模拟桥梁退化较为困难；数据驱动模型中回归模型使用简单，预测具有高效性，同时也能较好反映影响退化因素与桥梁状态的关系，但回归模型不符合桥梁退化的随机性，忽略了桥梁各构件之间的影响作用，且产生新数据时需要对模型进行更新；随机模型是目前运用较多的退化预测模型，其中马尔可夫链法广泛应用于桥梁管理系统，适用于区域路网级桥梁，但马尔可夫模型假定离散的转移时间间隔会导致预测精度下降；人工智能模型在一定程度上能避免回归模型、随机模型精度不够的局限性，具有较大发展潜力，但这种模型的使用往往需要更多的数据来保证预测精度。退化预测模型分类及优劣性如表2所示。

表2 退化预测模型分类及优劣性Table 2 Classification and pros and cons of degradation prediction models

2 桥梁养护时机

根据养护时间点桥梁养护可分为必要性养护和预防性养护[43-44]。必要性养护是结构性能指标达到阈值时即结构失效时对其的养护，必要性养护往往比预防性养护带来更高的性能提升，但其成本更高，预防性养护一般是为了略微改善桥梁的性能或延缓桥梁的恶化过程而进行的养护，以此保持桥梁结构性能在安全水平以上[45-46]，如图2所示。预防性养护又分为：基于使用的养护和基于状况的养护[47-48]，基于使用的养护不管桥梁结构或构件条件如何，定期维护或更换构件，基于状况的养护根据检测，按检测的结果采取相应措施。

图2 预防性养护和必要性养护[46]Fig.2 Preventive maintenance and essential maintenance[46]

传统的养护策略主要以日常养护和必要性养护为主，容易造成资源浪费及过度维护等后果，预防性养护已被证明经济有效[49]，预防性养护的核心思路是寻找养护成本和性能提升间的平衡点，未来桥梁养护将主要为预防性养护。

预防性养护的核心工作主要是成本效益分析及最优养护时机分析，成本效益分析主要是对桥梁养护的成本的计算与预测，分析养护方案能带来的社会经济效益，最优养护时机的确定主要是成本与性能提升最优平衡问题的建立与求解。

2.1 成本效益分析

桥梁退化预测模型建立之后，可得知桥梁在不同时期的服役状态以及退化到可接受最低水平的时期，就可以制定寿命周期内的养护方法。对于桥梁养护机构，需要利用有限的养护资金对桥梁进行养护，制定科学合理的养护策略，其养护成本分析尤为重要。国外较早提出全寿命周期成本分析(life-cycle cost analysis，LCCA)概念，通过有效的成本评价方法来评估劣化桥梁在整个寿命期内的成本支出的合理性。生命周期内养护成本不确定性大，LCCA将优化算法和概率统计方法结合在一起，评价养护带来的经济效果，并判断养护方案的优劣[50]。

中外学者对成本效益分析进行了大量研究，张春霞等[51]初步建立了桥梁预防性养护全寿命费用与优化方法的基本理论框架，将预防性养护费用表示为养护开始时间与养护间隔时间的函数，并在满足耐久性前提下，计算出最少的养护成本。曾勇等[52]提出了必要性维修、基于使用维修、基于状况维修3种维修方式的成本计算公式，并给出了3种维修方式在满足最低可靠性能指标时的年均成本。Hatami等[53]利用LCCA作为决策支持工具，用于桥梁管理中常见的桥面铺装维护决策、伸缩缝更换决策和桥面加宽与桥面更换决策。分析了每种决策下不同维护方案的成本净现值，给出了经济效果最好的方案。

生命周期内养护成本预测往往受多种因素影响，预测的精度需要进一步考虑。Wu等[54]构建了一个使用半马尔可夫过程的生命周期优化模型，并指出维修策略的LCCA受到许多成本不确定因素的影响，如折现率的波动以及交通量的变化，需要使用灵敏度分析或概率方法对成本不确定性进行研究。Nili等[55]结合遗传算法和离散事件仿真，提出了一种新的基于仿真的桥梁维修优化框架，在成本分析中考虑了维修的时间进度、工作区间、工作人员规划以及交通限制情况，并在实际案例中应用，结果证明了它在寻找最佳维护计划方面的高效以及估计成本方面的准确性。高楠等[56]综述了中外学者在桥梁养护成本预测方面考虑了桥龄、交通量、养护时间等影响养护成本因素的研究方法，介绍了各个模型在实际应用中的优势以及在未来研究过程中还可深入研究的方向。

总的来说，中外学者对养护成本预测进行了大量研究，其方法较为成熟，目前成本预测分析在单一桥梁或构件上使用较多，精度也较高，桥梁养护往往以某线路为单位考虑，路网内桥梁养护成本分析很重要，对于区域路网内的桥梁，不同桥梁不同病害导致的养护成本不一样，且不同桥梁养护成本影响因素存在差异，因此针对路网桥梁的成本分析还需进一步研究。

2.2 最优养护时机

制定桥梁合理养护策略关键在于找到最优养护时机，桥梁养护优化可分为单目标优化和多目标优化。

单目标往往以最低养护成本为目标，其优化计算得出单一最优养护方案不一定能满足桥梁管理人员对桥梁性能的特定要求，多目标优化的目标有可靠度、桥梁技术状况，预期生命周期成本、预期检查成本、预期养护成本、预期用户成本和桥梁冗余度等，利用Pareto最优条件的概念，多目标优化可以提供一组用于目标之间的权衡分析的最优解，其考虑了多个竞争目标的最佳平衡，通过多目标优化的应用，决策者可以更好地应对快速变化的环境。

Shim等[57]将桥面养护看作一个双目标优化问题，以桥面性能和养护成本作为优化目标，并提出一种适用于非凸问题且只产生Pareto最优解集的改进求解方法。Yang等[58]针对疲劳关键细节的检查和维护问题，以预期生命周期成本、预期检查成本和预期维护成本三目标进行优化计算，得到生命周期成本最低的检查维护方案，但该方法没有直接考虑结构的性能，只是考虑了成本的优化。

Kim等[59]以目标可靠度指标为约束，采用了双目标(桥梁网络可靠度和预期养护成本)、三目标(桥梁网络可靠度、预期养护成本和预期用户成本)、四目标(桥梁网络可靠度、预期养护成本、预期用户成本和桥梁网络冗余度)优化问题对一路网内桥梁进行分析，并对比了其优化结果，表明四目标优化的可靠性指标最高，因为只有四目标考虑了冗余度。由此可以看出，桥梁网络的可靠度指标受到考虑其他目标的影响，在考虑多目标时，结果往往更合理。

多目标优化问题求解方法主要有目标规划方法和智能方法，目标规划法求解多目标优化Pareto最优解一般难以保证准确度，智能方法，如遗传算法、粒子群优化算法等能更好适用多目标优化。Yang等[60]提出了一种退化桥梁网络生命周期管理的方法，考虑了由退化引起的桥梁故障相关的网络级风险，并以桥梁网络级风险和维护投资作为优化目标，利用遗传算法进行优化计算，获得最优的生命周期维护策略，包括维护计划和每个维护动作的成本。一般的智能算法往往也难以确保最优解的精确性，因而常常被视为元启发式算法，改进的智能算法目前应用越来越多。

Wang等[61]提出了一种非参数随机子集优化算法，用于有效地识别基于可靠性的重要度排序，为网级桥梁管理养护提供重要参考。黄天立等[62]提出了基于Gamma随机过程和遗传算法的锈蚀钢筋混凝土桥梁结构检测维护策略优化分析方法，得到寿命期望和检测维护成本预算下收益最大的检测维护策略Pareto最优解集。Yang等[63]对比了非支配排序遗传算法(non dominated sorting genetic algorithm-II, NSGA-II)和多目标粒子群算法(multi-objective particle swam optimization-II, MOPSO-II)，结果表明MOPSO-II更有效且能够得到全局解。

上述优化问题中桥梁性能往往依靠可靠度表征，而桥梁技术状况评分更为直观简洁，夏烨等[64]提出网级状态评估与管养策略优化框架，针对各类型数据建立了二次编码规则，通过人工神经网络得到最优桥梁技术状况退化模型，采用带精英策略的非支配排序遗传算法(NSGA-II)实现了路网级桥梁管养策略的机器寻优，并求解给出了某路网50座桥梁的未来3年的备选维修方案集。

当路网中桥梁数量较多时，计算成本较大，针对此问题又提出布谷鸟搜索[65]、多目标优化混合算法[66]等算法来解决。目前已经有很多学者对桥梁养护优化进行了研究，但算法的应用理论、高效性、精确性、全局最优等问题还需进一步研究。

总的来说，桥梁养护有较多的研究，各种多目标优化模型以及优化计算方法较为成熟，但仍存在优化目标如养护对结构性能提升效果与实际情况有一定误差以及优化计算成本大的问题，优化养护时机在工程实用中也未得到广泛体现。未来该领域的研究方向一是更智能的优化算法，高效、精确寻找最优养护时机，目前的研究主要是针对路网桥梁或者某单一桥梁，另一研究方向则是在路网-全桥-构件3个层面的综合养护策略。

3 结论

(1)物理退化模型基于材料及构件的物理性能演化来分描述结构的劣化过程，强调因果关联，可解释性强，但由于服役环境的复杂性以及外部荷载的随机性影响，桥梁性能演化机理复杂，目前少数的多因素退化模拟往往只是将各退化因素影响简单叠加，忽略了时间尺寸上的耦合性影响，此外，耐久性试验结果的可靠性受尺寸效应限制，基于真实服役环境与荷载模拟的大比例、足尺模型试验有待进一步的开展，多因素耦合作用下的桥梁长期性能演化机制解析与精准退化模型的建立仍有待进一步深入研究。

(2)桥梁结构退化过程本质上是随机的，回归模型建立了性态指标与时间之间的确定性关系，但忽略了随机变量和数据的不确定性影响；随机模型主要使用Weibull分布、Gamma分布等来描述退化过程，其准确性依赖检测、监测数据的长期积累；人工智能模型能够建立服役特征与结构性态指标间复杂映射的关联代理模型，影响参数的可解释性对于代理模型的评价具有重要研究价值。

(3)桥梁养护其数学本质可归纳为带约束多目标函数的优化求解问题，在目标函数的建立方面，由于病害类型、养护时间、历史养护情况、交通量、人工调度等参数与养护成本、养护时机等控制目标间的复杂隐性关系不易量化表达，导致显性目标函数较难建立，影响了养护成本与时机的控制精度，基于概率神经网络等人工智能算法，可望实现影响因素与控制目标之间的精确代理模型的建立；在目标函数的求解方面，路网内桥梁数量较多时，存在优化计算成本大、精确度低、容易陷入局部最优的问题，更具普适性的智能优化算法有待进一步研究。