高压高产气井油管柱强度安全分析
李喜成, 唐习之, 薛继彪, 詹宁, 张鹏翔
(1. 中国石油集团西部钻探工程有限公司国际工程公司, 乌鲁木齐 830000;2. 中国石油集团西部钻探工程有限公司吐哈钻井公司, 吐鲁番 838200)
油气井管柱是石油天然气开采作业中的必需设备,随着越来越多的深层油气资源进行勘探开发,油气井管柱所处的工作环境也急剧恶化,尤其是高温、高压、高产井“三高”油气井[1-3]。油井管柱生产环境恶劣,且井况和地下条件复杂,造成管柱受力状况差异较大,从而导致管柱变形、蠕动更加复杂且剧烈。因此,在生产作业过程中,管柱易出现塑性失效、断脱失效,导致管柱失效事故频繁发生,使得油气藏无法进行长久持续开采,给气井的开发带来了诸多问题,造成油气开采成本升高。
目前许多研究者对油气井管柱力学行为和管柱强度安全进行了研究。黄桢[4]建立了天然气在油管内流动的油管柱振动方程,计算表明油气经过油管内径变化部分、油管弯曲部分、节流阀等处会引起油气流速和油管压力的变化,进而诱发管柱振动。邓元洲[5]建立了管柱瞬态动力响应分析的有限元模型和预测管柱疲劳寿命的数学模型,分析表明振动是导致油管断裂的直接原因,气井产量、腐蚀和冲蚀程度对管柱疲劳寿命起决定作用。李子丰[6]介绍了油气井杆管柱力学基本原理、油气井杆管柱的运动状态、油气井杆管柱动力学基本方程,综述了管柱的磨损和腐蚀与冲蚀、管柱的剩余强度和疲劳强度预测等方向的进展与争论。桑果[7]针对川西地区管柱建立油管在自重、内外压力、黏滞摩阻力、油套摩擦力、井眼弯曲以及封隔器等因素下的管柱力学模型,分析井下套管的活塞效应、螺旋弯曲效应、膨胀效应以及温度效应对管柱的影响。陈立超等[8]通过利用扫描电镜及二次电子图像、背散射图像对陇东地区煤层气井管柱腐蚀机理进行研究,研究发现陇东地区煤层气井N80油管钢在高矿化度、地层水环境发生强烈CO2腐蚀作用,形成多层结构腐蚀产物FeCO3膜。温后珍等[9]采用比例尺1∶10油套管模型进行管柱在套管中的屈曲行为试验研究,研究结果表明,管柱受压屈曲会导致摩擦力增大;管柱相对套管的偏心对轴向力的分布影响很小;证明了管柱力学分析理论中轴向力计算时油管与套管同心的假设是合理的。张颖等[10]针对高产气井中管柱振动问题建立特殊螺纹接头密封面在动载荷作用下接触应力的力学模型,结果表明:公接头密封球面半径越小,接触应力越大且越集中,密封接触宽度也越小。
从目前研究现状看,主要集中在管柱力学行为、管柱冲蚀机理、管柱振动机理与动力响应、管柱腐蚀机理、管柱螺纹强度分析等方面,对高压高产气井油管柱在受到内压、外压、轴力、扭矩、弯矩等多种载荷变化下的强度分析研究不足。为此,建立高压高产气井油管柱动力学模型,通过高压高产气井油管柱安全系数法和高压高产气井油管柱三轴应力法对高压高产气井油管柱强度进行校核。对高压高产气井油管柱强度安全的研究,可为管柱设计提供理论指导。
1 高压高产气井油管柱动力学振动模型的建立
如图1所示,在高压高产气井开采过程中,高压高产流体从地层进入井筒,经管柱到达平台井口,高速流动的流体会诱发管柱的振动,易导致管柱发生振动破坏,管柱连接失效等事故。因此,需要研究高压高产下气井管柱的振动和强度情况。

图1 气井开采过程示意图Fig.1 Schematic diagram of gas well production process
1.1 高压高产气井油管柱动力学方程组
从高产高压气井管柱系统中取出管柱单元体进行受力分析,如图2所示。
根据管柱单元的转角和扭矩的本构关系可得
(1)
根据轴向扭矩平衡方程可得
(2)
式中:J为管柱转动惯量,kg·m2;G为管材剪切模量,GPa;ρP为管柱密度,kg/m3;t为时间,s。
管柱绕x轴的转角和弯矩可表示为
(3)

(4)
根据牛顿第二定律推导出y方向的力平衡可得

(5)
管柱x方向力矩平衡可得

(6)
式中:ρf为流体密度,kg/m3;E为管柱弹性模量,GPa;IP为管柱极惯性矩,m4;If为流体极惯性矩,m4;Af为流体横截面面积,m2;AP为管柱横截面面积,m2。
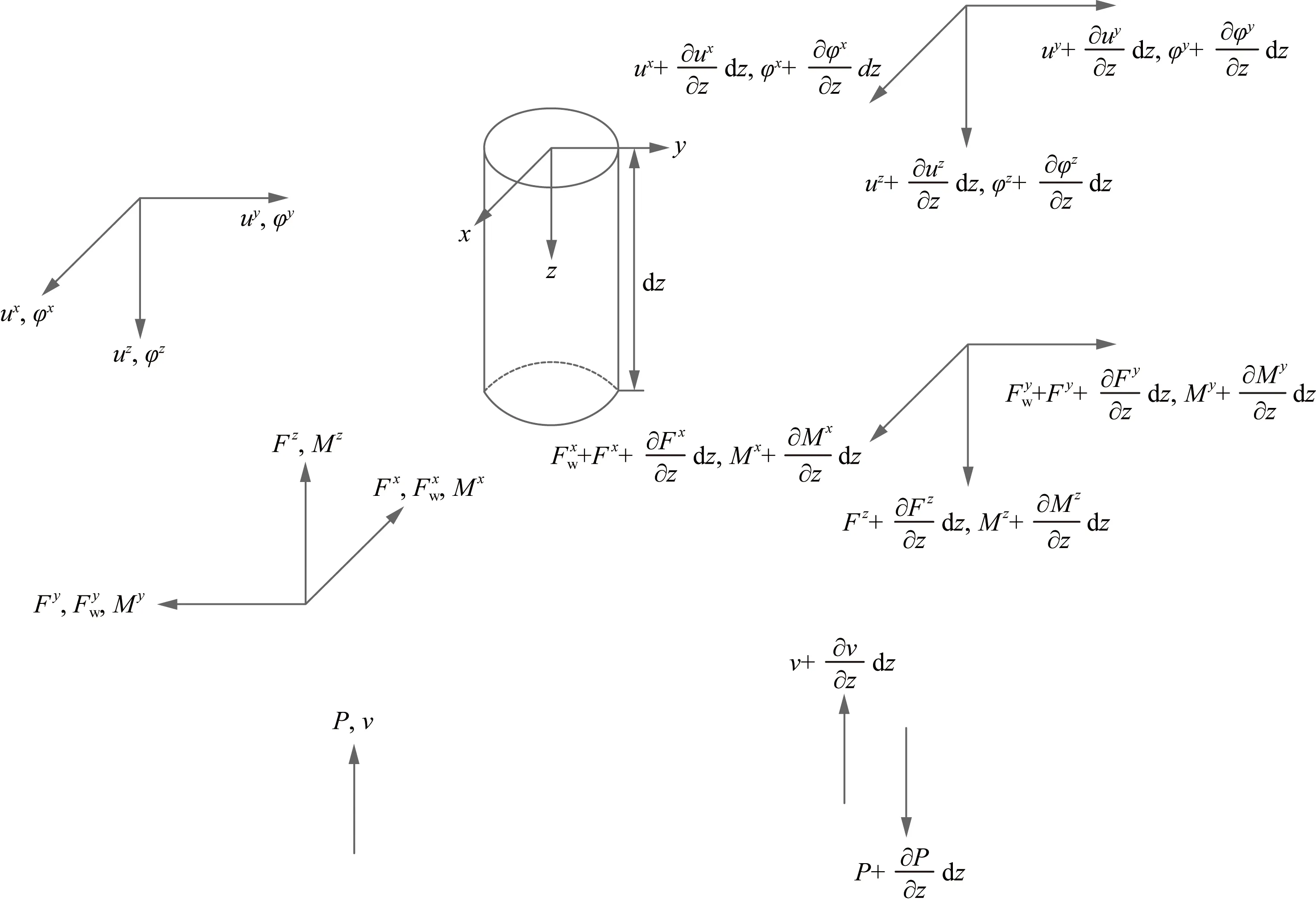
z轴方向为管柱轴线方向;x、y轴为垂直于管柱方向;M、φ、F、u分别为油管柱所受内部流体作用产生的弯矩、转角、力、位移;P、v分别为流体的压强和流速;Fw为套管对油管柱的作用力图2 管柱单元受力图Fig.2 Force diagram of the string unit
管柱绕y轴的转角和弯矩可表示为

(7)

(8)
根据牛顿第二定律推导出x方向的力平衡可得
(9)
管柱y方向力矩平衡可得

(10)
根据管道结构的本构方程和动力方程可得
(11)

(12)
根据流体的连续性方程和动量方程可得
(13)

(14)

1.2 模型求解
1.2.1 特征方程
上述管柱振动方程为拟线性双曲线偏微分方程,采用特征线法来求解双曲线偏微分方程[11-12]。特征线法的主要思路是将偏微分方程转化为常微分方程,即特征方程,然后通过采用一阶差分法将它转化为特定的差分格式方程进行编程求解。
首先将管柱系统划分为若干计算单元,如图3所示,由于各特征波的波速不同,特征线和空间线不能交于网格点,因此,需要对管柱的空间步长和时间步长做一定的规定,计算程序框图如图4所示。根据线性差分理论,为保证计算格式的稳定,需满足:
(15)
式(15)中:Δzmin为管柱系统中计算单元最小;amax为特征波波速最大;Δt为时间步长。
然后通过采用一阶差分法将特征方程转化为特定的差分格式方程,差分结果如下。
(1) 管壁轴向扭矩。
(16)
(17)
式中:C+为正向特征线;C1为管柱轴向管材剪切模量;C-为反向特征线;M为弯矩;C为管材剪切模量;模型方程中符号上标表示方向;下标表示对该参量的一阶偏导。

i、n为管柱划分的节点数,其中,i为管柱节点的第i个位置,n为管柱节点的第n个位置图3 管柱节点单元划分图Fig.3 Diagram of node element division of pipe string

图4 求解流程图Fig.4 Solution flow chart
(2)y-z平面的剪力和弯矩。
(18)
(19)
(20)
(21)
式中:C2为x-z平面纵向管材剪切模量;C3为x-z平面横向管材剪切模量;ap3为波速;模型方程中符号上标表示方向;下标表示对该参量的一阶偏导。
(3)x-z平面的剪力和弯矩。
(22)
(23)
(24)
(25)
(4) 管壁轴向应力。

(26)

(27)
式中:C4为平面纵向管材剪切模量;P为压力;模型方程中符号上标表示方向,下标表示对该参量的一阶偏导。
(5) 沿轴向的流体压强和流速。
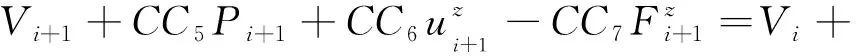
(28)
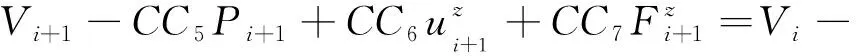
(29)

1.2.2 边界条件
高压高产气井油管柱系统时域分析是在定解条件下求解高压高产气井油管柱动力学方程组的数值解,因此,在对管柱进行动力响应计算时,应建立管柱初始状态和定解条件。高压高产气井油管柱动力学初始条件,即流体与管柱结构相互作用之前管柱系统的应力、弯矩、扭矩、位移、压强及流速。对于管柱系统,其初始应力、弯矩、扭矩、位移及相对压强可看作零进行处理,初始状态的流速考虑为流体以一定恒定流速在管柱内流动。高压高产气井油管柱的上端在平台处固定,限制了管柱上端的横向、纵向位移和转动,管柱上端边界为[13-14]
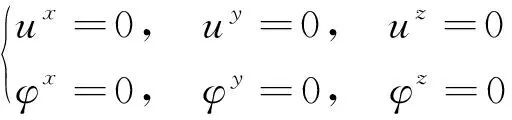
(30)
下端在封隔器处固定,限制了管柱下端的横向、纵向位移和转动,管柱下端边界为

(31)
1.3 高压高产气井油管柱强度校核
1.3.1 高压高产气井油管柱安全系数法校核
高压高产气井油管柱上的应力状态主要有:内压和外压作用在高压高产气井油管柱上所产生的径向应力σr和环向应力σθ,轴向产生的拉应力和压应力σF;高压高产气井油管柱弯曲所产生的附加弯曲应力σM;剪力f横向产生的横向剪切力τ1,因此,一般情况下高压高产气井油管柱的任一点应力状态都是复杂的应力状态,故在进行高压高产气井油管柱强度校核时,根据第四强度理论进行安全系数校核[15-16]。
(1)内压和外压作用下高压高产气井油管柱的应力分析。根据弹性力学的厚壁圆筒理论知识可知,环向应力σθ(r,s)和径向应力σr(r,s)为
(32)
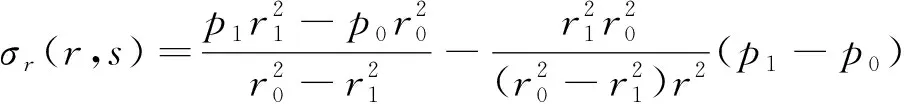
(33)
式中:r为管柱半径,m;s为管柱深度,m;p1为内压,MPa;p0为外压,MPa;r1为高压高产气井油管柱内半径,m;r0为高压高产气井油管柱外半径,m。
(2)轴向应力(高压高产气井油管柱在此处受压为正、受拉为负)为
(34)
式中:A0为油管外横截面积;A1为内横截面积。
(3)根据前面求得的高压高产气井油管柱上任一点处的弯矩M(s),则在弯矩所在平面内距离轴心r的轴向弯曲应力σM为
(35)
(4)根据材料可知高压高产气井油管柱的剪切应力的计算公式为
(36)
(37)
式中:f为应力;τf为剪切应力。
τf(s)远远小于σM(r0,s),因此剪切应力一般可以忽略。根据四强度理论,可得高压高产气井油管柱的相当应力为
(38)
则相应的强度条件为
(39)
式(39)中:σs为管柱材料的屈服极限;ns为安全系数,一般ns取1.25。
在实际工作过程中高压高产气井油管柱的安全系数n应满足:
(40)
1.3.2 高压高产气井油管柱三轴应力法校核
因为高压高产气井油管柱在开采过程中,是处于较为复杂的三轴应力状态,还需要对高压高产气井油管柱强度进行三轴应力校核,指高压高产气井油管柱在三轴应力下,高压高产气井油管柱抗外挤、抗内压和抗拉的能力,它主要与高压高产气井油管柱自身的屈服强度相关。高压高产气井油管柱三轴应力强度校核具体如下[17-18]。
(1)高压高产气井油管柱三轴抗挤强度计算公式为
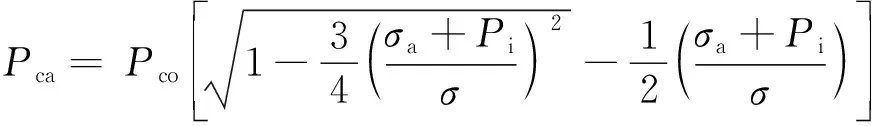
(41)
式(41)中:Pca为三轴抗挤强度,MPa;Pco为抗挤强度,MPa;σa为轴向应力,MPa;σ为屈服强度,MPa;Pi为管内液体压力,MPa。
(2)高压高产气井油管柱三轴抗内压强度计算公式为

(42)
式(42)中:Pba为三轴抗内压强度,MPa;Pbo为抗内压强度,MPa;Po为管外液体压力,MPa;ri为高压高产气井油管柱内半径,MPa。
(3)高压高产气井油管柱三轴抗拉强度计算,公式为
(43)
式(43)中:Ta为三轴抗拉强度,MPa;To为抗拉强度,MPa。
2 工程实例分析
根据前面提出的高压高产气井油管柱动力学振动模型,对某井管柱的动力学特性进行了模拟分析。对于高压高产气井油管柱多用外径114.3 mm、外径88.9 mm和外径73.0 mm,选取钢级N80高压高产气井油管柱,屈服强度为758 MPa,表1为某高压高产气井油管柱的主要参数,表2为管柱系统的计算参数。
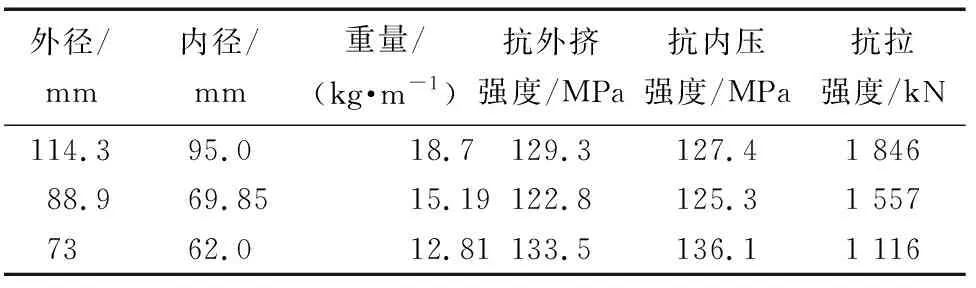
表1 管柱的主要参数Table 1 Main parameters of the pipe string

表2 管柱系统计算参数Table 2 Calculation parameters of the string system
2.1 高压高产气井油管柱不同产量下振动分析
通过上述管柱动力学模型计算得到不同产量下管柱的振动位移,图5为管柱不同产量8×105、1×106、12×105m3/d下横向位移对比云图。可以看出,管柱的横向位移随着产量的增大而增大。这是因为:随着产量的增加,流过单位截面积的流量大,在相同的管径内流速增加,对管柱的冲击力增大,管柱振动更大。对于高产井,当管柱内流量增大时,流体在管柱的压力降低得更快,压力波动更大,长期的作用可能会使得管柱失效破坏,甚至管柱断裂。因此,需要对高压高产气井油管柱进行安全校核分析。
2.2 高压高产气井油管柱基本应力分析
运用上述建立的高压高产气井油管柱动力学模型,计算出管柱在外径114.3 mm下典型位置处H300 m、H600 m、H1 660 m和H2 540 m(H为深度)位置处的管柱横向振动应力随时间的变化关系。图6为管柱不同位置的横向振动应力随时间变化关系曲线,可以看出,在0~20 s内管柱(H300 m、H600 m)的横向振动应力幅值比管柱(H1 660 m和H2 540 m)大,管柱横向应力振动幅值较大,随后振动应力趋于稳定,管柱处于交变应力状态。其中,管柱H300 m的应力幅值范围为-47.9~58.8 MPa;管柱H600 m的应力幅值范围为-95.5~98.2 MPa;管柱H1 660 m的应力幅值范围为-11.9~8.8 MPa;管柱H2 540 m的应力幅值范围为-5.6~3.9 MPa。
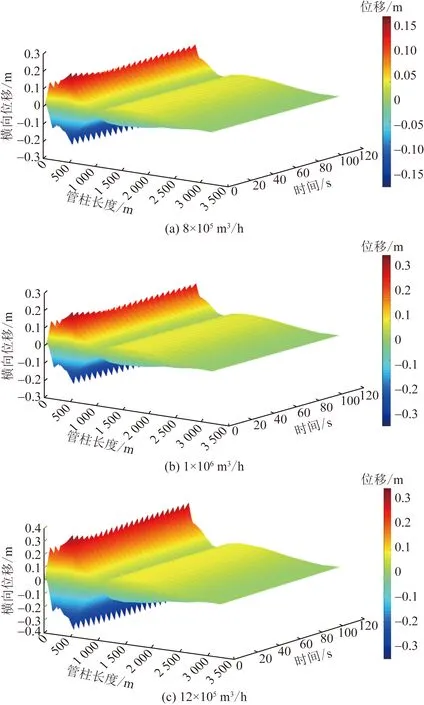
图5 管柱不同产量下横向位移对比云图Fig.5 Contrast cloud diagram of lateral displacement of pipe string under different production rates

图6 管柱的横向振动应力时间历程图Fig.6 Time history of the transverse vibration stress of the pipe string
图7为管柱在H300 m、H600 m、H1 660 m和H2 540 m位置处的管柱纵向振动应力随时间变化历程。可以看出,管柱H300 m和H600 m的纵向振动应力幅值小于管柱H1 660 m和H2 540 m纵向振动应力,越靠近管柱下部管柱的纵向振动应力越大,在0~10 s,管柱纵向应力振动幅值较大。其中,管柱H300 m的应力幅值范围为-74.1~63.8 MPa;管柱H600 m的应力幅值范围为-89.6~105.3 MPa;管柱H1 660 m的应力幅值范围为-122.7~132.3 MPa;管柱H2 540 m的应力幅值范围为-136.4~152.6 MPa。

图7 管柱的纵向振动应力时间历程图Fig.7 Longitudinal vibration stress time history diagram of pipe string
图8(a)为管柱的最大轴向力振幅,其中在管柱的井口位置处轴向力最大,最大值为925.3 kN小于管柱抗拉强度1 846 kN。图8(b)为管柱的最大应力振幅图,其中在管柱的井口位置处Mises应力最大,最大值为237.04 MPa,但未超过管柱的屈服强度758 MPa,即管柱在开发过程中,由内部流体诱发管柱振动产生的应力没有达到管柱的极限强度,管柱未发生破坏,但可能管柱处于交变低应力的情况下,可能后续也会对管柱产生损伤。
2.3 高压高产气井油管柱尺寸对管柱应力的影响
为了更进一步的分析管柱内部流体引起不同尺寸管柱振动的应力变化,计算分析外径88.9 mm和外径73.0 mm的应力分布,如图9和图10所示。从图9~图11中可以看出,外径114.3 mm的应力振动幅值最小,而外径73.0 mm的振动应力幅值最大,因此大尺寸管柱有利于降低高速流体诱发管柱的振动问题。通过这些数值和曲线说明管柱在高速流体作用下,属于不规则的交变振动,管柱内的交变应力复杂化。从图11中可以看出,管柱井口处轴向力最大,但并未超过管柱所能承受拉力的警戒线。因此在管柱设计过程中应该考虑设计减震器,以便减小开发过程中管柱振动带来的损伤。

图8 管柱轴向力及最大应力分布Fig.8 Axial force and maximum stress distribution diagram of the pipe string
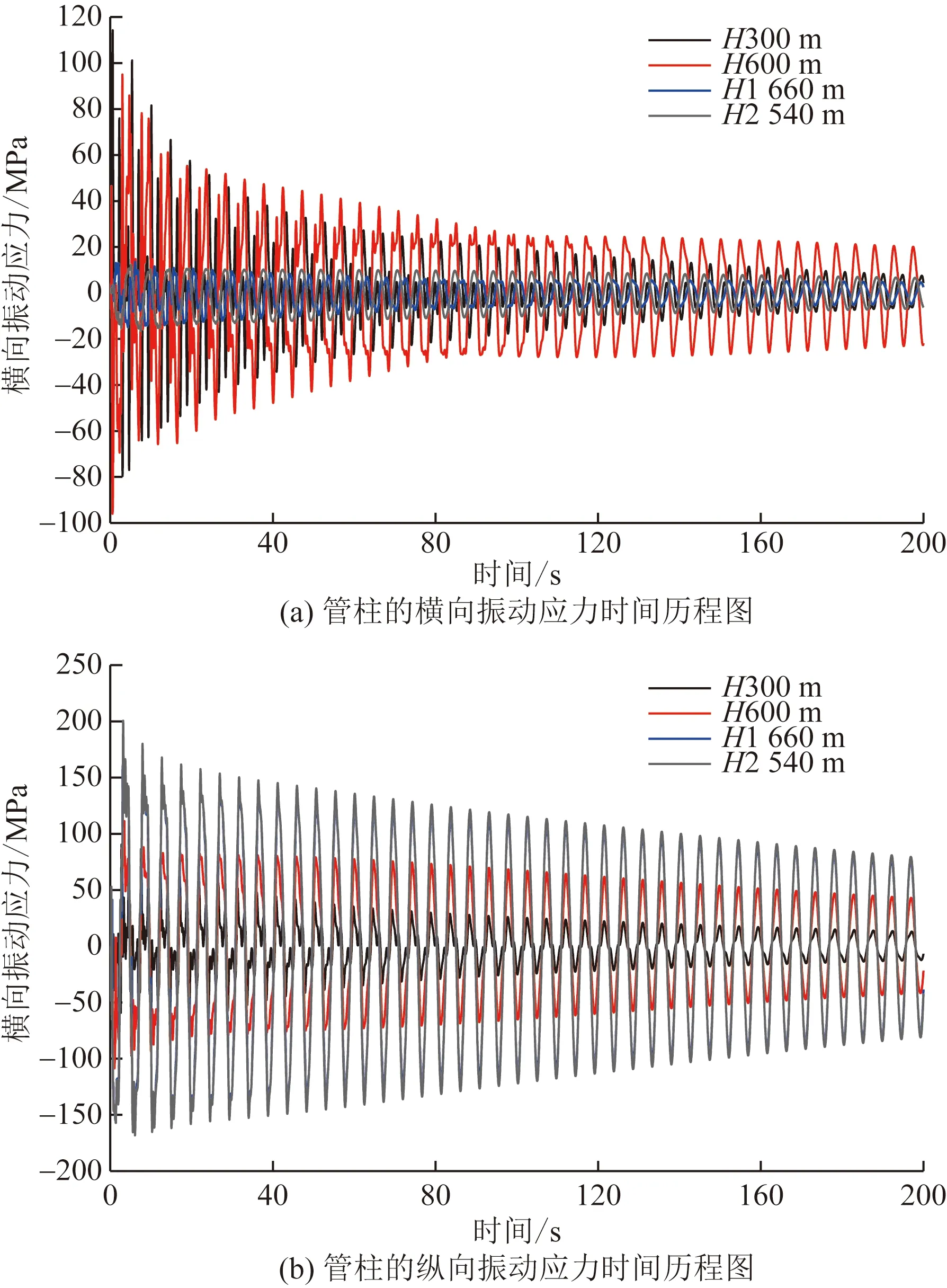
图9 外径88.9 mm管柱下管柱的横向、纵向振动应力时间历程图Fig.9 Time history diagram of the transverse and longitudinal vibration stress of the pipe string under the pipe string size of 88.9 mm

图10 外径73.0 mm管柱下管柱横向、纵向振动应力时间历程图Fig.10 Time history of the transverse and longitudinal vibration stress of the pipe string with a pipe string size of 73.0 mm

图11 管柱不同尺寸下轴向力分布Fig.11 Axial force distribution under different sizes of pipe string
对管柱强度进行安全系数法校核,各向参数及结果如表3所示。管径114.3 mm安全系数n=4.90(n>1.25),管径88.9 mm安全系数n=5.24(n>1.25),管径73.0 mm安全系数n=4.47(n>1.25)。对管柱强度进行三轴强度校核,结果如表4所示。可以看出,管柱的强度是足够的,但是由于高压高产开发过程的振动产生的复杂交变应力,可能会导致管柱上的其他设备的振动损伤,其中在纵向上振动可能导致管柱螺纹接头产生松动而导致破坏,同时管柱可能会在低应力状态下产生疲劳破坏。在管柱设计和运行过程中,为了降低管柱的振动,首先可以增加管柱的结构尺寸,降低管柱内流体的流量,流体的流速,降低流体的冲击载荷。因此对于高产高压井,须采用大尺寸管柱,以便降低由于振动引起的管柱损伤问题。
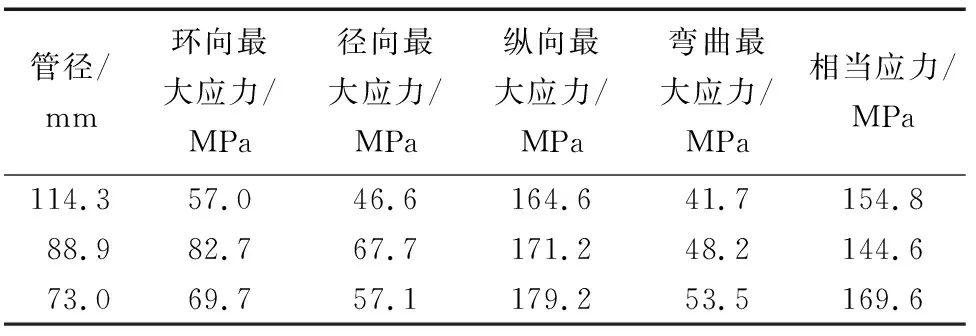
表3 管柱各向应力及结果Table 3 All-directional stress and result of pipe string

表4 管柱三轴强度Table 4 Triaxial strength of pipe string
3 结论
建立高压高产气井油管柱动力学模型,通过高压高产气井油管柱安全系数法和高压高产气井油管柱三轴应力法对高压高产气井油管柱强度进行校核,对高压高产气井油管柱基本应力和管柱尺寸对管柱应力的影响进行分析,经过分析,得出如下主要结论。
(1)随着产量的增加,管柱的横向位移不断增大。当流过单位截面积的流量增大时,在相同的管径内流速增加,对管柱的冲击力增大,管柱振动更大。对于高压高产井,当管柱内流量增大时,流体在管柱的压力降低得更快,压力波动更大,长期的作用可能会使得管柱失效破坏,甚至管柱断裂。因此,需要对高压高产气井油管柱进行安全校核分析。
(2)在0~20 s内管柱(H300 m、H600 m)的横向振动应力幅值比管柱(H1 660 m和H2 540 m)大,管柱横向应力振动幅值较大,随后振动应力趋于稳定,管柱处于交变应力状态。管柱H300 m和H600 m的纵向振动应力幅值小于管柱H1 660 m和H2 540 m纵向振动应力,越靠近管柱下部管柱的纵向振动应力越大,在0~10 s内,管柱纵向应力振动幅值较大。管柱在井口位置处轴向力最大。
(3)由于高压高产开发过程的振动产生的复杂交变应力,在纵向上振动可能导致管柱螺纹接头产生松动而导致破坏,同时管柱可能会在低应力状态下产生疲劳破坏。在管柱设计和运行过程中,为了降低管柱的振动,首先可以增加管柱的结构尺寸,降低管柱内流体的流量,流体的流速,降低流体的冲击载荷。因此对于高产高压井,须采用大尺寸管柱,以便降低由于振动引起的管柱损伤问题。

