连续刚构桥跨中节段混凝土接缝抗弯性能研究

朱小霖， 容洪流 ,2,3*， 余春霖， 肖璐， 巫志文,2

(1.广西大学土木建筑工程学院， 南宁 530004； 2.工程防灾与结构安全教育部重点实验室， 南宁 530004； 3.广西特殊地质公路安全工程技术研究中心， 南宁 530004； 4.中国建筑第八工程局有限公司， 南宁 530004)

随着国家道路建设事业的快速推进，中国的桥梁建设也大步向前。连续刚构桥以其刚度大，跨越能力较强，更多地受到设计者的考虑。大跨径连续刚构桥多采用悬臂浇筑法施工，不可避免地在桥梁节段间留下施工接缝，而接缝处的薄弱影响梁段的刚度，增加桥梁下挠的风险。接缝界面凿毛质量差，甚至不进行凿毛，接缝处混凝土漏浆，浇筑不饱满等质量问题削弱了接缝附近混凝土的力学性能。随着连续刚构桥跨径的不断提升，接缝问题带来的下挠隐患越来越无法被忽视，许多学者针对大跨径桥梁接缝问题进行了研究。

贾朋涛等[1]、李庆桐等[2]研究发现，桥梁设计中若忽略竖向接缝的存在会造成桥梁实际变形远大于预期值。熊英[3]通过研究得出先浇梁段在接缝处凿毛的质量以及接缝混凝土的密实度对接缝的影响较大。李国平等[4]对分段成型的桥梁混凝土结构中常用的四类接缝进行耐久性研究，认为接缝是影响混凝土耐久性最关键的部位。赵若昀等[5]通过试验得出混凝土强度越高，预制混凝土桥面板湿接缝收缩应力越大。Kim等[6]通过超高性能混凝土预制节段接缝的直剪试验研究发现，齿键数量的增加的同时破坏荷载也逐渐上升。姜海波等[7-8]研究发现，在剪跨比小于或等于2.0时,预制节段干接缝体外预应力混凝土梁的抗剪承载力小于相应的整体式混凝土梁的抗剪承载力。沈殷等[9]认为当节段预制拼装混凝土桥梁接缝面的抗剪承载力计算不可忽略剪应力的非均匀分布特征。袁爱民等[10]提出，配筋剪力键胶接缝直剪承载力计算的建议公式。刘杰等[11]以虎门大桥辅航道桥为原型，制作分段浇筑简支梁进行试验，得出节段接缝抗剪刚度降低系数约为0.244。Veletzos等[12]、Kim等[13]对桥梁接缝抗震进行研究，发现加入抗剪连接结构可以减弱震后的损伤。Gopal等[14]研究发现，增加齿键数量可有效提高超高性能纤维混凝土齿键接缝的抗剪承载力。

已有研究表明,桥梁节段接缝力学性能对桥梁的整体安全性能的影响不可忽略[15]。不同学者针对接缝某一特定方面进行了具体的研究，但是针对大跨径连续刚构桥悬臂施工缝抗弯性能的研究较少。采用节段混凝土接缝抗弯试验模拟连续刚构桥悬臂施工，考虑截面配筋的直径、布筋间距、界面处理和预应力施加等因素对接缝抗弯性能的影响，分析各因素影响规律，对比分析不同弯曲下挠理论，为桥梁跨中节段接缝抗弯下挠控制提供参考依据，对保障整桥的使用安全、促进预应力连续刚构桥健康发展有积极意义。

1 原材料及试验方法

1.1 原材料

1.1.1 水泥

本试验配制不同配合比试件，在水泥选用上有华润上思P.П 42水泥和华润上思P.П 52.5水泥两种，所选用水泥各项物理性能指标如表1所示。

1.1.2 集料

(1)粗集料。试验碎石采自灵山县新金鸡石场，碎石粒径有4.75～9.5 mm，9.5～19 mm两种规格。碎石的吸水率为0.33%，针片状颗粒含量为6.0%，表观密度为2 704 kg/m3。

(2)细集料。细集料选用广西合浦县石湾镇建林砂场的河砂，其细度模数为2.8，表观密度为2 650 kg/m3，堆积密度为1 574 kg/m3，含泥量为2.2%。

1.1.3 掺合料

试验掺合料采用广西钦州蓝岛粉煤灰，粉煤灰等级为Ⅰ级。其性能指标如表2所示。

表2 粉煤灰的性能指标Table 2 Performance index of fly ash

1.1.4 水和外加剂

外加剂采用广西新广建GJHP-S号聚羧酸缓凝型减水剂。外加剂掺量1.0%时，减水率为34%。拌合用水采用本地井水，经检测符合《混凝土用水标准》(JGJ 63—2006)要求。

1.2 混凝土配合比设计

考虑不同混凝土强度等级可能对试验结果产生影响，试验设计3种混凝土配合比。通过混凝土强度差异，区分不同配合比试件。配合比设计分为三组，A组设计混凝土强度等级为C40；B组设计混凝土强度等级为C50；C组设计混凝土强度等级为C55。各组配合比如表3所示。

表3 不同标号混凝土配合比Table 3 Concrete mix ratio of different grades

表3所示的三组混凝土配合比中：A组粉煤灰掺量为15%，外加剂掺量为1.2%，水胶比为0.39；B组粉煤灰掺量为15%，外加剂掺量为1.6%，水胶比为0.32；C组粉煤灰掺量为10%，外加剂掺量为1.7%，水胶比为0.31。

1.3 主要试验方法

1.3.1 抗弯试验设计依据

混凝土梁式构件以弯曲作用下的挠度作为设计控制的主要指标。在《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)中，桥梁构件受弯的挠度采用结构力学的方法进行设计计算，本文根据此方法推导三分点加载方式下的试件弯曲下挠公式，以此进行节段接缝抗弯试验设计。

在结构力学中，挠度方程为

(1)

式(1)中：MF为荷载F作用在试件的某一位置x时所产生的弯矩；E为弹性模量，MPa；I为截面惯性矩，mm4；EI为抗弯刚度；C1、C2为常数。

挠度计算采用叠加法处理，先计算F/2作用于三分点时的挠度，再叠加计算合力F作用时的挠度。利用连续性与边界条件计算得到荷载F/2单独作用于左边三分点时跨中挠度v1，可表示为

(2)

式(2)中：F为荷载；l为试件支承跨径。

因此总挠度f为

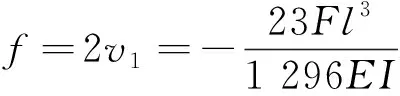
(3)

依据式(3)和三分点加载方式对节段接缝抗弯试验进行设计。

1.3.2 试验方案

(1)素混凝土抗弯试验方案。对于素混凝土试件，跨中截面考虑试件是否分段以及分段截面凿毛与否对接缝抗弯性能的影响。混凝土配合比采用B组，整浇试件、分段凿毛试件和分段不凿毛试件每组制作试件3个，共制作9个试件。抗弯试件尺寸为150 mm×150 mm×550 mm，试件编号及参数如表4所示。

(2)钢筋混凝土抗弯试验方案。钢筋混凝土抗弯试件尺寸为150 mm×150 mm×550 mm，跨中截面考虑分段和不分段两种状况，研究接缝对混凝土节段抗弯性能的影响。

试验通过分段浇筑来模拟桥梁悬臂施工状况，对分段截面采用不同的配筋方案，研究布筋间距、布筋形式等因素对接缝抗弯性能的影响。

布筋间距为30～90 mm，每组间隔10 mm。钢筋分别选用Φ8 mm和Φ12 mm两种型号，Φ8 mm和Φ12 mm除了每层钢筋数不同，其他情况均相同，Φ8 mm试件每层布置两根钢筋，Φ12 mm试件每层布置一根钢筋，Φ8 mm钢筋试件的布筋如图1所示。

表4 试件编号及对应参数Table 4 Specimen number and corresponding parameters

图1 试件尺寸Fig.1 Specimen size

素混凝土和钢筋混凝土的整浇试件均采用标准塑料试模进行制作，分段浇筑试件均采用定制木试模制作。钢筋混凝土试件的钢筋笼采用两根短钢筋绑吊在试模之中，以保证钢筋骨架在试件合适的位置并满足混凝土保护层厚度的要求。木试模中间采用15 mm横隔板进行分隔，横隔板比侧板高3 cm。普通钢筋需要预先穿过隔板进行绑扎。

钢筋混凝土试件的混凝土配合比采用B组，试件编号及设计参数如表5所示。

(3) 预应力混凝土弯曲试验方案。跨中截面同样考虑分段和整浇两种状况，通过改变施加在试件上的纵向预应力大小，研究接缝和预应力大小节段抗弯性能的影响。

预应力筋采用上下两层布置，每层布筋1根，预应力管道布置间距为70 mm。预应力螺杆采用Φ12 mm光圆钢筋加工而成，螺杆长为650 mm，在螺杆两端各开牙口150 mm。试件预应力采用后张法施加，为使螺杆能够顺利穿过预应力管道，塑料套管内径较螺杆直径大2 mm。

预应力混凝土抗弯试件尺寸为150 mm×550 mm，试件混凝土配合比采用B组，试件编号及设计参数如表6所示。

1.3.3 试验加载与数据处理

试验采用WAW-1000B型液压数显微机万能试验机进行加载，通过调节夹具支座至设计跨径，旋转试件90°使浇筑面朝向正前方，标注出两个支承位置和三分点加载位置线，将试件平稳放置在支座上并与夹具均匀接触，如图2所示。

试件加载时应控制加载速率在0.15～0.25 kN/s，在加载开始前读取跨中千分表读数，在加载过程中每5 kN对千分表挠度读数进行一次记录，直至试件破坏卸载。试验结束后将记录数据绘制成为荷载-挠度曲线。

表5 试件编号及对应参数Table 5 Specimen number and corresponding parameters

表6 试件编号及对应参数Table 6 Specimen number and corresponding parameters

图2 试件加载图Fig.2 Test-piece loading

2 试验结果与讨论

2.1 接缝对素混凝土节段接缝抗弯试验结果与分析

3种状况下的素混凝土试件跨中开裂截面如图3所示。

素混凝土试件在整浇试件、分段不凿毛和分段凿毛3种状况下对应的抗弯强度如图4所示。试验结果表明，整体浇筑试件的抗弯强度最大，分段凿毛试件次之，分段不凿毛试件的抗弯强度最小。从开裂后的试件截面来分析原因，整体浇筑试件的骨料在跨中开裂截面上交错分布，表面粗糙、断面棱角多，分布较为均匀，试件两端骨料在开裂前融合充分，提供良好的抗弯能力；而分段凿毛试件骨料填充不佳，仅有较细骨料相互嵌挤，黏结性能中等。凿毛处理是为了去除表面浮浆，漏出截面骨料，以增加新旧混凝土结合能力。考虑到凿毛后易对原有骨料的稳固性产生影响，处理后混凝土骨料露出效果也难以与整浇状态一致，因此分段凿毛试件抗弯强度较整浇试件有所降低。

图3 试件跨中开裂截面Fig.3 Mid span cracked section of specimen

图4 不同截面处理方式的抗弯强度值Fig.4 Flexural strength values of different cross-section treatments

相较于凿毛处理试件，分段不凿毛试件的断面基本保持平整。开裂后，裂缝两端混凝无土骨料相互嵌挤现象，黏结性能最差，抗弯强度最低。在桥梁悬臂施工过程中，梁段间的接缝使得桥梁的整体性受到破坏，抗弯开裂荷载减小，更易产生开裂，加剧桥梁跨中下挠。

综合素混凝土节段接缝抗弯试验分析认为，分段浇筑接缝处的浮浆会影响截面混凝土的黏合性，采用凿毛手段处理后，分段接缝处混凝土骨料接触面积增大，混凝土结合效果得到增强。考虑到试验仅采用手工凿毛方式处理，在桥梁施工中对接缝处混凝土采用机械凿毛会使结合效果进一步提升。

2.2 钢筋混凝土节段接缝抗弯试验结果分析

钢筋混凝土试件破坏形态如图5所示。

图5 钢筋混凝土试件破坏形态Fig.5 Failure modes of reinforced concrete specimens

2.2.1 接缝对节段抗弯性能的影响

Φ8 mm和Φ12 mm两种钢筋混凝土试件在不同荷载作用下分段浇筑与整体浇筑的跨中挠度结果如图6所示。可以看出，在相同挠度下，两种钢筋试件的整浇试件开裂荷载始终大于分段浇筑试件开裂荷载。结合素混凝土抗弯试验结果认为，由于分段接缝处存在明显薄弱截面，试件开裂由分段接缝处产生，而分段界面较为平整，在加载过程中分段浇筑试件一旦产生开裂，裂缝将迅速向上扩展，开裂后分段浇筑试件的抗弯能力发生严重衰减，而不存在分段薄弱截面，因此整体浇筑试件在抗弯能力上好于分段浇筑试件。

图6 整体浇筑与分段浇筑荷载挠度对比Fig.6 Comparison of load displacement between integral casting and sectional casting

两种钢筋试件在相同荷载作用下整浇试件与分段浇筑试件的挠度结果如图7所示。

由图7可知，整体浇筑的Φ8 mm和Φ12 mm钢筋试件在相同荷载下的挠度均小于对应的分段浇筑试件。对比整体浇筑与分段浇筑试件的挠度差发现，两组试件在约75 kN时挠度差最小，在其余荷载大小作用时，挠度差均有所增大。

分段浇筑试件由于开裂较早，在加载水平较低时，试件破坏较整体浇筑试件更为严重，此时挠度差较大；当荷载继续增大，整体浇筑试件的裂缝增加，下挠速度加快，此时整体浇筑试件与分段浇筑试件的挠度差缩小；当荷载增大到75 kN后，分段浇筑试件的钢筋开始屈服，此时整体浇筑试件与分段浇筑试件的挠度差重新增大。对比两种浇筑方式在相同荷载作用下的挠度，经过计算，Φ8 mm钢筋试件分段浇筑较整体浇筑时刚度下降31.6%；Φ12 mm钢筋试件分段浇筑较整体浇筑时刚度下降36.7%。

图7 不同浇筑情况下试件挠度值Fig.7 Comparison of specimen torsion under different casting conditions

图8 试件不同布筋间距下的挠度值Fig.8 Deflection value of under different reinforcement spacing

综合分析可知，分段浇筑的接缝是导致钢筋混凝土梁刚度下降的重要因素。

2.2.2 布筋间距对节段接缝抗弯性能的影响

不同钢筋混凝土试件布筋间距的挠度变化规律如图8所示。

由图8可知，相同布筋间距的试件，随着荷载的增大，跨中挠度值呈线性增大趋势。在相同荷载作用下，试件布筋间距越大，试件的挠度值越小；由拟合曲线(图8)可知，随着试件布筋间距的线性增大，试件挠度值呈现非线性减小关系，布筋间距较大时，试件挠度减小放缓。综合以上分析认为，加大钢筋布筋间距对节段接缝性能的提升有帮助，但随着布筋间距的不断增大，提升效果有所减弱。

2.2.3 布筋形式对节段接缝抗弯性能的影响

定义刚度剩余率系数k，用于表示开裂后与开裂前刚度的比值，同时定义Bcr为开裂后试件刚度，B0为开裂前试件刚度，则三者关系为

Bcr=kB0=kE0l0

(4)

式(4)中：E0为钢筋混凝土复合弹性模量，MPa；l0为钢筋混凝土复合抗弯惯性矩，mm4。

钢筋混凝土试件的复合刚度使用混凝土与钢筋材料特性按复合公式求出。

E0I0=EcIc+EaIa

(5)

式(5)中：Ec为混凝土弹性模量，MPa；Ea为钢筋弹性模量，MPa；Ic为混凝土抗弯惯性矩，mm4；Ia为钢筋骨架抗弯惯性矩，mm4。

将式(4)和式(5)代入式(6)得到试件挠度差值与荷载差值的变化关系为

(6)

式(6)中：Δy为挠度差值，mm；ΔP为荷载差值，kN。

从而得出刚度剩余率k为

(7)

由式(7)得到钢筋混凝土分段浇筑试件开裂后的刚度剩余率k计算结果如图9所示。

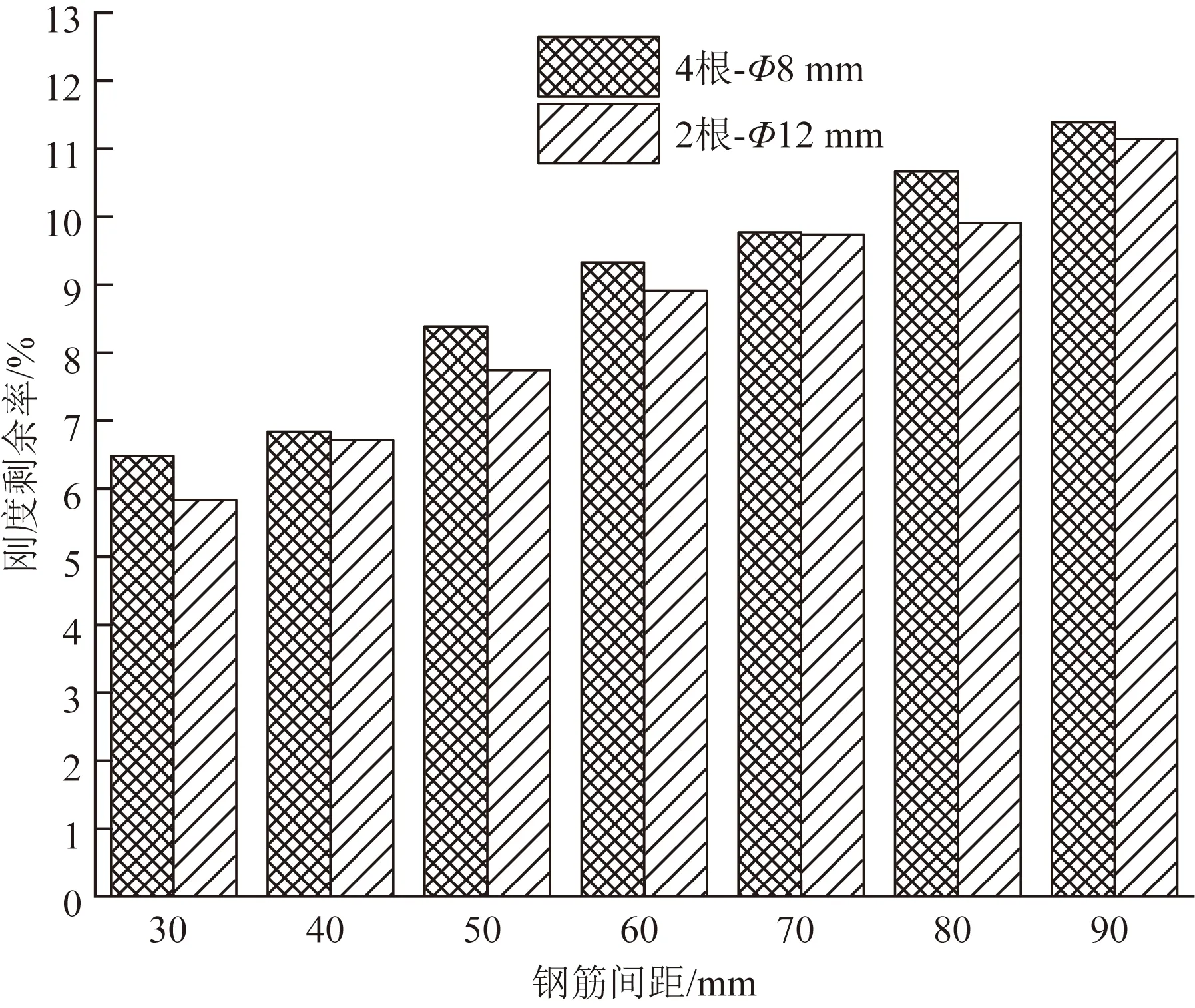
图9 分段浇筑试件开裂后的刚度剩余系数Fig.9 Stiffness reduction factor of different reinforcement arrangement forms

由图9中的k值大小可以看出，分段浇筑试件开裂后刚度下降明显，两种布筋形式下试件的刚度损失均超过85%，最高剩余刚度仅为11%左右。在相同布筋间距下，采用四根Φ8 mm钢筋的布置方式比采用两根Φ12 mm钢筋的布置方式剩余刚度更大。

由试验结果分析认为，相较于采用两根钢筋的布置方式进行抗弯，在试件开裂后，四根钢筋布置方式参与截面抵抗弯曲时，对混凝土整体约束效果更好。四根Φ8 mm钢筋截面配筋率为0.893%，两根Φ12 mm钢筋截面配筋率为1.005%。四根Φ8 mm钢筋的布置形式在更节省钢筋的情况下，对节段接缝抗弯的效果也更好。

综合两种布筋形式的试验结果认为，采用分散布筋的方式效果更佳；在钢筋直径的选取上，分散布筋方式可以考虑选用偏小一号钢筋，在降低配筋率节约成本的同时，也能取得更好的节段接缝抗弯效果。

2.3 预应力混凝土节段接缝抗弯试验结果分析

预应力混凝土试件破坏后形态如图10所示。

图10 预应力混凝土试件破坏形态Fig.10 Failure modes of prestressed concrete specimens

2.3.1 接缝对节段抗弯性能的影响

取相同荷载作用下，预应力整体浇筑试件与预应力分段浇筑试件的挠度结果如图11所示。

图11 相同荷载作用下预应力试件挠度Fig.11 Comparison of Deflection of Segmented and Whole Cast Specimens under the Same Load

由图11可知，在相同荷载作用下，预应力分段浇筑试件的挠度远大于整体浇筑试件，因为分段浇筑试件的接缝降低了试件的整体刚度，不利于试件的抗弯，使得预应力混凝土整浇试件的抗弯性能要好于分段浇筑试件抗弯性能，与素混凝土试件和钢筋混凝土试件试验结果一致。

2.3.2 预应力大小对节段接缝抗弯性能的影响

预应力试件的预应力-挠度曲线如图12所示，荷载-挠度曲线如图13所示。

由图12可以看出，预应力混凝土试件分为开裂前和开裂后两个阶段。在预应力混凝土试件开裂前，由于试件内预应力产生的抵抗下挠弯矩较大，预应力的作用在试件内占主导地位，试件跨中挠度值为零。随着加载的继续，预应力产生的抵抗下挠弯矩逐渐被施加的弯曲荷载平衡，接缝处混凝土粘

图12 预应力-挠度曲线Fig.12 Prestress-deflection curves

图13 荷载-挠度曲线Fig.13 Load-deflection curves

结失效后，试件分段薄弱面上产生开裂，开裂后试件的挠度增长趋势基本一致，随着荷载的增大，挠度增加。此外，通过对比不同预应力大小试件发现，预应力越大的试件开裂越迟，因此得出提高预应力大小可以延缓试件开裂的时间。

由图13可知，施加预应力越小，试件跨中挠度越大。以20 kN作为预应力施加基准，随着预应力损失的增大，试件挠度的变化呈现先慢速增长后快速增长趋势。预应力在12～20 kN时，预应力处于较高水平，施加高水平的预应力更有助于控制试件开裂后的裂缝扩展；预应力在8～12 kN时，试件预应力处于较低水平。此时分段试件受弯，预应力抗弯作用很快被施加荷载抵消，试件过早的开裂会产生更大的挠度。由此认为分段浇筑试件施加高水平的预应力能更有效地控制跨中挠度。

3 不同弯曲下挠理论对比分析

根据“非零应矩”试验，文献[15]提出了弯曲定律：在弹性纯弯曲时，弯应矩与线应变成正比。弯曲定律中使用Gw表示弯曲弹性模量，采用绝对静矩来表示抗弯能力。绝对静矩相较于静矩的区别，在于静矩通过形心取矩时为零，而绝对静矩通过形心取矩不为零。

受到弯曲定律的启发，在弯曲过程中对混凝土受力取微元体进行分析，现有弯曲理论将作用到微元体上的正应力简化为一个微小平均应力，而这个新的弯曲理论用绝对静矩代替截面惯性矩表征截面抗弯能力，认为即使微元体取得再小，微元体上的正应力在上下部位仍存在大小差异，使得微元体存在上下切割趋势，混凝土在这种趋势下的开裂受剪切模量控制。当混凝土切向受力大于其抗剪切能力时，混凝土产生破坏。梁体受弯时，梁顶或梁底作为最薄弱环节参与弯曲，应与弯曲弹性模量Gw取值相关。梁顶与梁底距中性轴距离为h/2，其中h为梁高，考虑使用h/2与剪切模量G组合表示Gw。

根据以上分析，将Gh/2与绝对静矩|sz|的乘积替换三分点加载下试件的跨中挠度计算公式中的EI，得到新理论的跨中挠度计算公式为

(8)

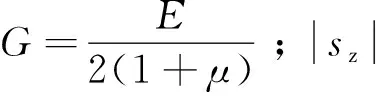
将式(8)和式(3)两种新旧理论挠度公式计算结果分别与不同标号素混凝土整浇试件弯曲下挠试验结果进行对比，如图14所示。

图14 试验结果与计算对比Fig.14 Comparison between test results and calculation

由图14可以发现：从总体上看，现行理论计算值比实测值偏小，试件平均实测挠度约为现行理论计算值的1.25倍，对于桥梁安全性设计是不利的。

新理论挠度计算值比的预测结果偏大，原因可以从试验误差方面进行分析：①在试验设计时认为，万能压力机对试件产生的弯矩使试件只发生竖向弯曲。但实际情况中，由于试件高度方向与宽度方向的尺寸一致，在加载过程中受到夹具等因素的影响，施加荷载中的一部分使试件发生了横向抗弯，导致实际用于竖向弯曲的荷载相较荷载记录值要小，当荷载全部作用于试件竖向弯曲时测得的挠度值应有所增大，会更接近新理论的预测值；②由于试件跨径较小，在进行弯曲挠度测量时，跨中挠度受三分点加载影响较大。虽然试验的挠度测量点设在跨中，但三分点加载上部夹具的施荷点距离较近，在试件小变形时，试件的跨中挠度与三分点挠度几乎一致，因此采用跨中挠度计算公式存在较大误差，应使用三分点挠度公式进行对比分析更合理。综上所述，在排除试验误差的情况下，认为新理论的挠度计算更接近实测。

4 结论

对分段混凝土试件在不同界面处理方式下的抗弯性能进行研究，考虑界面凿毛、截面配筋、预应力作用等因素的影响，对比分析不同弯曲下挠理论，得出如下主要结论。

(1)浮浆对接缝处混凝土的黏结效果影响显著，凿毛处理能有效地提高混凝土界面黏结能力。

(2)截面布筋间距对节段接缝试件抗弯的影响是非线性的，布筋间距过大或过小都会导致试件破坏荷载的降低。随着布筋间距增大，试件抗弯刚度的提升会逐渐减弱。

(3)采用分散布筋的方式更利于钢筋抗弯效果的发挥。在配筋率更低的情况下，采用四根Φ8 mm钢筋布置较采用两根Φ12 mm钢筋布置的开裂剩余刚度更大。

(4)纵向预应力钢筋对节段接缝抗弯的影响主要在于延缓试件开裂的时机，施加高水平的预应力更有效地控制分段浇筑试件的跨中挠度。

(5)不同标号素混凝土整浇试件弯曲下挠试验结果表明，现行挠度公式计算结果均小于混凝土试件受弯下挠试验实测结果；在偏安全的情况下，以绝对静矩代替惯性矩的挠度计算值更接近实测值。