基于线性扩张状态观测器的电流谐波抑制

段 超，刘亚静，孙章军，任 武，李 琳，刘 乐

(1.北京航天控制仪器研究所，北京 100039；2.北京交通大学 电气工程学院，北京 100044)

0 引 言

永磁同步电机(PMSM)有着体积小、功率密度大和效率高等诸多优点，广泛应用于数控机床、机器人和航空航天等领域[1]。PMSM目前普遍采用的控制策略为矢量控制，通过坐标变换，使PMSM的控制效果可媲美直流电动机控制效果。在PMSM矢量控制系统中，由于功率开关器件的电压死区、PMSM本身的非线性因素以及信号反馈传感器的检测误差等因素，给系统带来了所不期望的扰动，扰动通过坐标变换在电流环中表现为电流谐波形式。电流谐波的存在会造成PMSM的转矩脉动，影响系统性能。

国内外学者对抑制电流环中电流谐波进行了大量研究，文献[1]对主流的电流谐波抑制策略进行了综述，其中讲到了自抗扰控制。自抗扰控制(ADRC)是由我国学者韩京清提出的一种先进控制策略，其核心部分为扩张状态观测器(ESO)[2-4],目前在电机控制领域有着大量的研究与应用[5-11]。其中文献[5]详细分析了线性扩张状态观测器(LESO)的参数选取对PMSM矢量控制系统的性能影响，并给出了针对PMSM的 LESO参数整定步骤。文献[6]将ADRC与滑模控制(SMC)结合应用于PMSM的鲁棒控制；文献[7-8]将ADRC应用于PMSM矢量控制系统的速度环，其中文献[7]采用双LESO来提高PMSM速度控制的抗扰能力；文献[8]通过对LESO降阶提高了扰动观测速度与精度。文件[9]采用新型ESO实现了周期性转矩脉动的有效抑制。文献[6～9]均是将ADRC或其中的ESO应用于速度环，由于系统速度环数学模型较复杂，有着计算量较大的缺点。

部分学者对ADRC或ESO在电流环中的应用也进行了研究，文献[10]通过构造电流环ESO来补偿SVPWM的死区效应影响；文献[11]构造电流环ADRC来改善控制系统的时间延迟影响；均取得了很好的效果。

本文针对电流谐波的抑制问题，设计了电流环LESO来抑制电流谐波，分析了LESO和整个电流环的稳定性并进行了参数整定，随后给出了一种与电流环传统PI控制进行性能对比的方法。最后通过仿真验证了电流环LESO对电流谐波抑制的有效性。

1 电流环线性扩张状态观测器设计

采用id=0矢量控制策略下的PMSM电流环控制框图如图1所示，其中的Gid(s)与Giq(s)分别表示id、iq电流控制器的传递函数。工程中电流控制普遍采用比例(P)控制或比例积分(PI)控制。

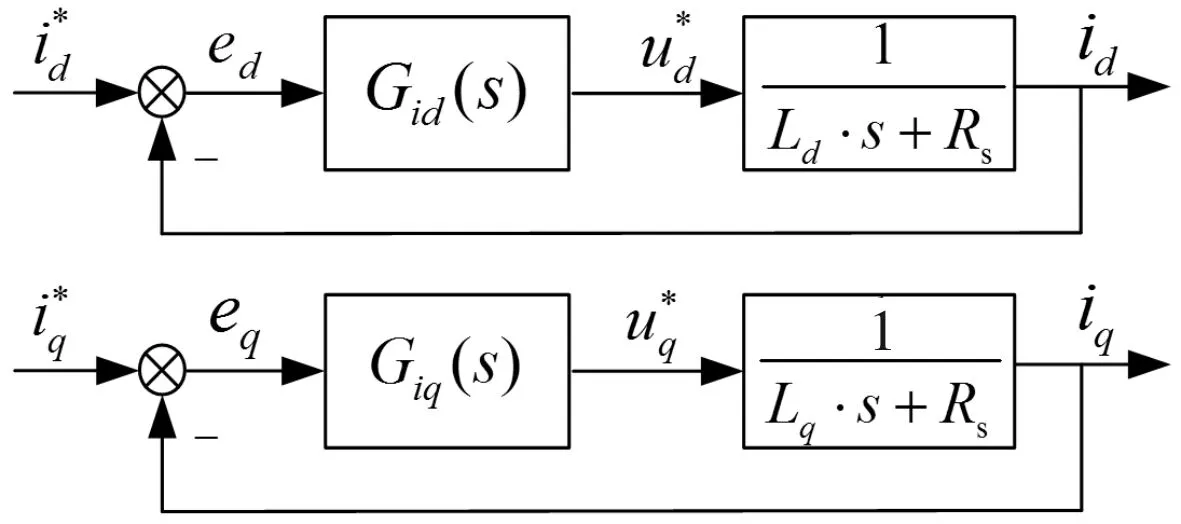
图1 电流环控制框图

实际PMSM矢量控制系统中，由于逆变器的电压死区、电流采样偏差和电机本体设计不合理等因素的存在，会在矢量控制系统中引入扰动，这里统一记为外部扰动δ，δ为非线性。δ通过坐标变换在电流环内表现为电流谐波形式，记d轴电流谐波扰动为δd，q轴电流谐波扰动为δq。引入了电流谐波的电流环控制框图如图2所示。

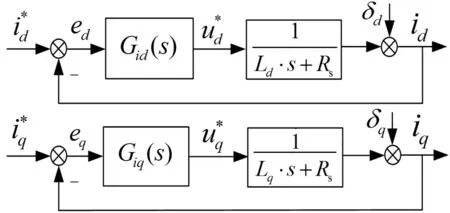
图2 引入了电流谐波的电流环控制框图

由图2可得电流环的数学模型为

(1)

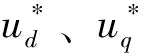
从式(1)可知，电流环d、q两轴的数学模型形式相同，下面以q轴为例进行电流控制器的设计与分析，d轴电流控制器的设计与分析同q轴。

由式(1)可得q轴数学模型状态方程

(2)

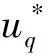
式(2)可简化为

(3)

式中，记f为总扰动，包含δq和内部未知变量。

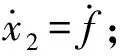
(4)

依据式(4)可构造电流环线性状态观测器(LESO)如式(5)所示，用于观测提取电流环中的总扰动f。

(5)

式中，β01，β02为LESO的待整定参数；z1为iq的估计值；z2为f的估计值。当β01，β02整定合适时，可得

(6)

将总扰动f的估计值z2进行反馈补偿

(7)

由式(3)、式(6)和式(7)可得

(8)

对比式(8)和式(3)可知，一个非线性系统简化为一个一阶线性积分系统。将简化后的线性一阶积分系统进行比例闭环控制

u0=Kad·(r-x1)

(9)

式中，Kad为电流环比例系数；r为q轴电流给定值。

由式(8)、式(9)可得采用了LESO的电流环闭环传递函数为

(10)

由式(10)易知，比例系数Kad>0，系统稳定。图3给出了采用LESO的q轴电流环控制框图，虚线框内为采用LESO的q轴电流控制器。d轴电流控制器设计同理。

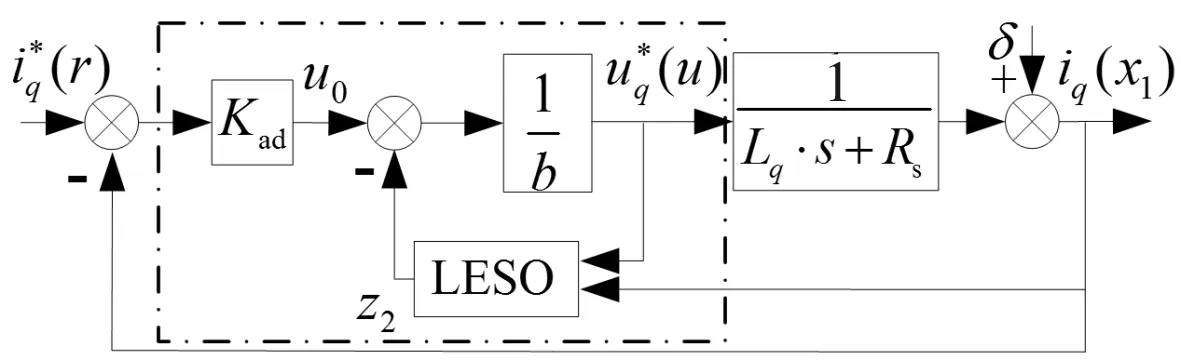
图3 采用LESO的q轴电流环控制框图

2 稳定性分析

2.1 LESO稳定性分析

与式(4)相对应的电流环状态矩阵方程组为

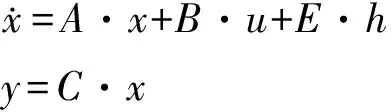
(11)

构造系统的全维状态观测器为

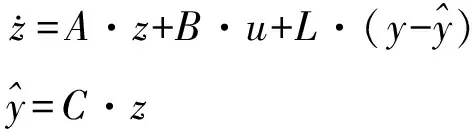
(12)

式中，L=[β01β02]T；为增益矩阵。

式(12)即为电流环LESO。记LESO估计误差为ei=xi-zi(i=1,2)。式(11)与式(12)相减可得误差状态矩阵方程为

e=(A-LC)·e+E·h

(13)

可求取误差状态矩阵方程的特征多项式为

λ(s)=det·[s·I-(A-LC)]=s2+β01·s+β02

(14)

当h有界，且β01>0，β02>0，所构造的线性扩张状态观测器BIBO稳定。

2.2 电流闭环跟踪误差稳定性分析

由式(6)、式(7)、式(9)可构造状态反馈矩阵方程为

u=F·z+Q·r

(15)

式中，F=(1/b)[-Kad-1]；z=[z1z2]T；Q=Kad/b。

结合式(11)、式(12)、式(15)可得采用了LESO的电流环状态矩阵方程为

(16)

求取式(16)的特征值为

(17)

已知Kad>0,β01>0，β02>0；r作为给定信号，是有界的；只要h有界，即总扰动f可微，则采用LESO的电流环BIBO稳定。

3 参数整定

由式(10)可知，采用LESO的电流环可等效为一阶惯性环节，电流环的带宽等于比例系数Kad。可通过调节Kad来调节电流环带宽。

接下来对LESO的参数进行整定。由式(5)求取输出信号z1、z2关于输入信号y和u的传递函数为

(18)

易知LESO的特征多项式为

λ(s)=s2+β01·s+β02

(19)

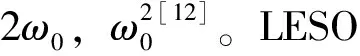
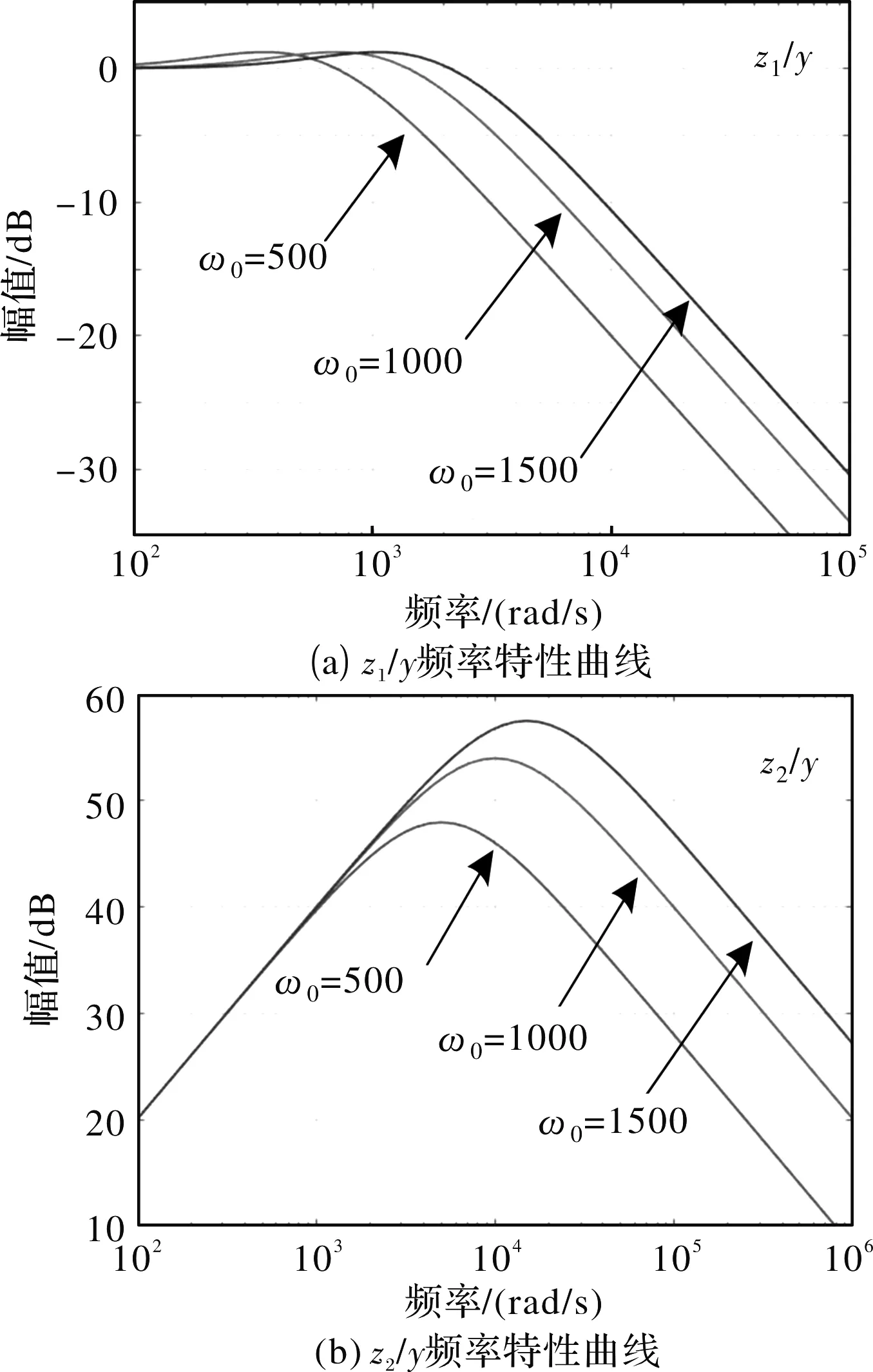
图4 LESO输入/输出信号频率特性曲线

4 与传统PI电流控制器性能对比

由前3小节理论分析可知，若LESO参数β01，β02选取合理，可实现电流谐波的有效抑制。采用LESO的电流环等效框图如图5所示。

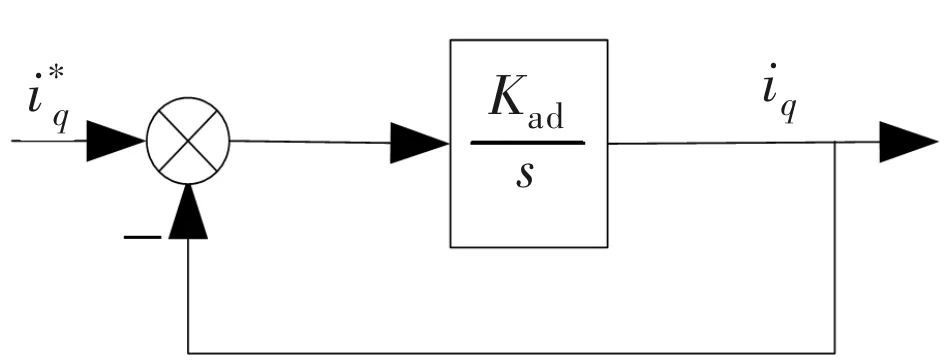
图5 采用LESO的电流环等效框图

采用传统PI控制器的电流环控制框图如图6所示。

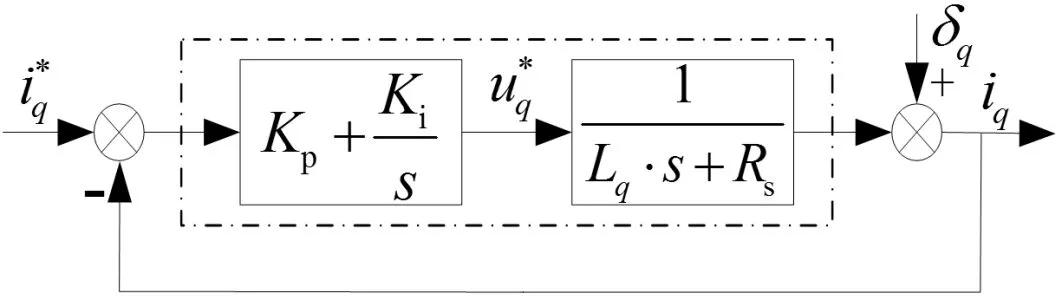
图6 采用PI控制器的电流环

令Kp=Kad·Lq，Ki=Kad·Rs；则PI控制器传递函数为Kad·(Lqs+Rs)/s，与PMSM电流环数学模型抵消分子分母后，采用PI控制器的电流环等效框图如图7所示。

对比图5与图7可知，采用LESO的电流环对电流谐波的抑制效果要优于电流环PI控制器。

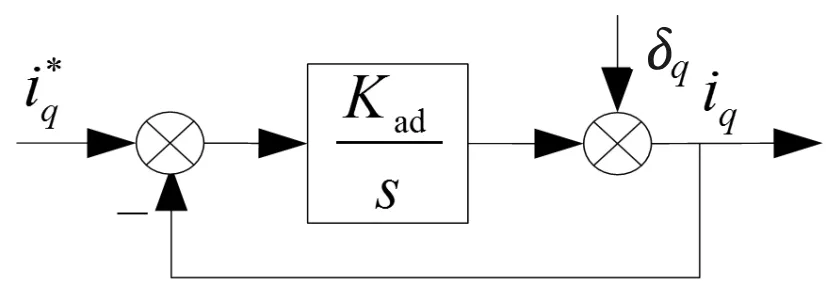
图7 采用PI控制器的电流环等效框图

5 仿真验证

电流环采用了LESO的PMSM矢量控制系统框图如图8所示，速度环仍采用PI调制策略。

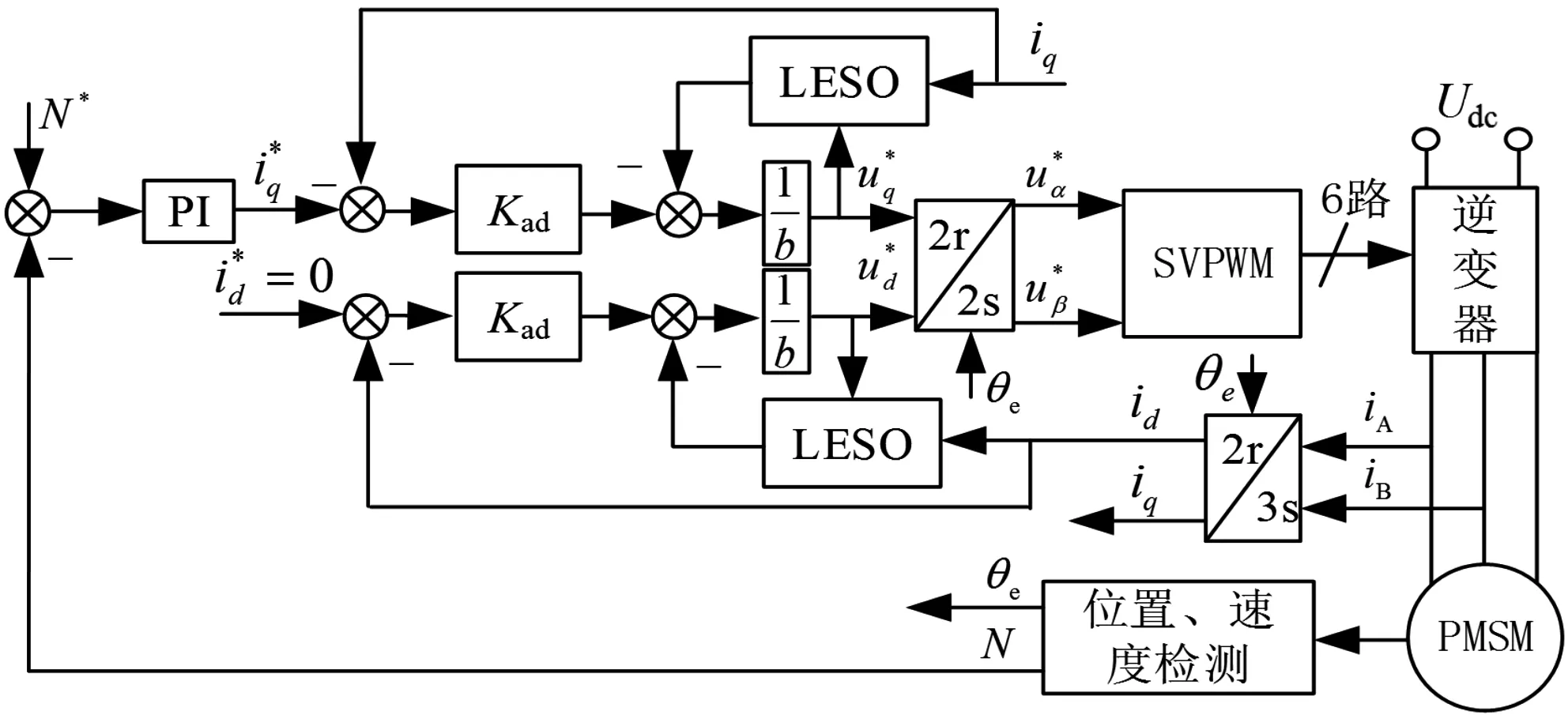
图8 电流环采用LESO的PMSM矢量控制系统框图

在Matlab/simulink软件平台上依据图8构建PMSM矢量控制系统进行仿真。电机仿真参数设定为实际项目用永磁同步力矩电机参数，如表1所示。

表1 电机仿真参数

控制系统其它参数设定如下：母线电压28 V；功率管开通关断死区TBD=2×10-6s；电流环LESO参数ω0=1500，比例系数Kad=100；速度环PI控制器比例系数Kp_v=0.05，积分系数Ki_v=2；负载转矩TL=0.35 Nm；给定速度N*=50 r/min。

为进行性能对比，同时构建电流环、速度环均采用PI控制器的PMSM矢量控制系统进行仿真。依据第4小节对电流环PI控制器设定参数，电流环比例系数Kp_i=0.6，积分系数Ki_i=665，其余参数同上。

图9给出了控制系统的三相电流仿真波形，其中图9(a)为电流环采用PI控制时的三相电流波形，图9(b)为电流环引入LESO控制时的三相电流波形。对比图9(a)和图9(b)可知，电流环采用LESO的控制系统，相电流正弦度更好。图10给出了图9中A相电流的谐波分析结果，其中图10(a)对应图9(a)中A相电流谐波分析结果，图10(b)对应图9(b)中A相电流谐波分析结果。由图10可知，A相电流中主要电流谐波成分为5次和7次谐波。电流环采用PI控制时，A相电流5次谐波成分占2.27%，7次谐波成分占2.88%，总谐波失真率为4.60%。电流环引入LESO时，A相电流5次谐波成分占1.44%，同比减少了0.83%；7次谐波成分占2.24%，同比减少了0.64%；总谐波失真率为3.56%，同比减少了1.04%。

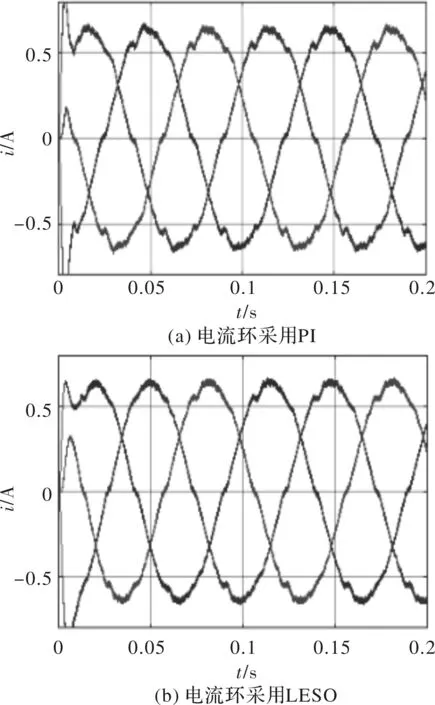
图9 三相电流仿真波形

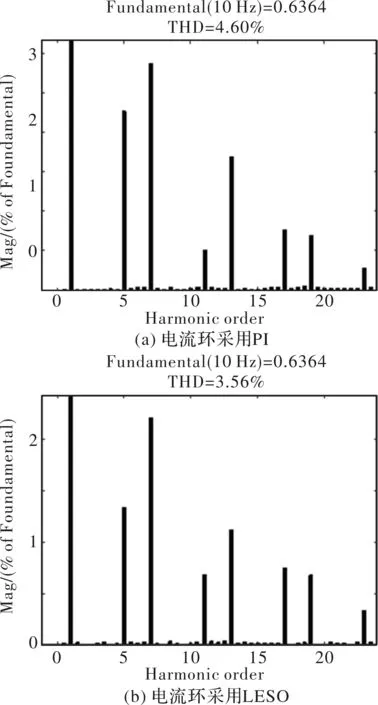
图10 A相电流的谐波分析结果

图11给出了PMSM的电磁转矩Te仿真波形，从图中可知，电流环采用PI控制的系统有着较明显的转矩脉动现象，电流环采用LESO的控制系统，转矩脉动得到了较好的抑制。图12给出了对应于图11的Te谐波分析结果。其中图12(a)为电流环采用PI 控制时的Te谐波分析结果，图12(b)为电流环引入LESO控制时的Te谐波分析结果。对比图12(a)与图12(b)可知，相比于电流环采用PI控制，电流环采用LESO时，电磁转矩Te的总谐波失真率从3.45%下降到3.05%，减少了0.4%。

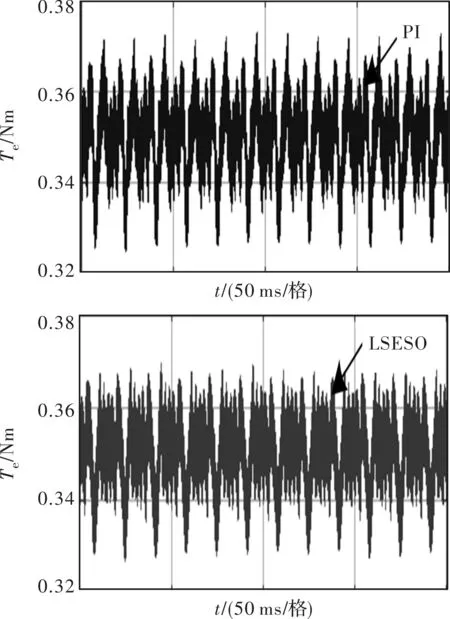
图11 电磁转矩Te仿真波形

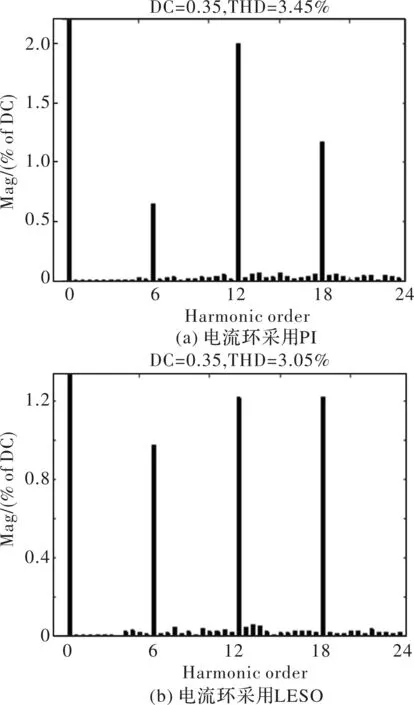
图12 电磁转矩Te谐波分析结果

6 结 语

本文设计了电流环LESO用来抑制电流谐波，通过理论分析证明了LESO和整个电流环的稳定性。给出了LESO和整个电流环的参数整定方法，其中电流环带宽正比于比例系数Kad，LESO参数ω0的大小理论上与电流谐波的抑制效果成正相关。

通过理论分析对比了采用LESO的电流环与采用PI控制的电流环对电流谐波的抑制能力，并进行了仿真验证。验证了电流环采用LESO对电流谐波有着较好的抑制效果，进而抑制PMSM转矩脉动。