基于精确子域模型的双定子磁通反向电机磁场解析计算

邹定琛，曹江华

(华南理工大学 电力学院，广州 510641)

0 引 言

磁通反向电机(FRM)由双凸极永磁电机发展而来，其绕组中的磁链呈双极性变化，相较于磁链单极性变化的双凸极永磁电机，磁通反向电机的功率密度更大；但相较于传统永磁电机，磁通反向电机的永磁体和绕组都放置在同一个定子上，定子空间更加拥挤，限制了其功率密度的提升[1]。为了进一步提升磁通反向电机的功率密度，文献[1]提出了双定子磁通反向电机(DS-FRM)，该电机将永磁体与绕组分开放置在内外定子上，相较于传统磁通反向电机，双定子的拓扑能够解除永磁体和绕组的空间冲突问题，同时能够在永磁体用量更少的情况下提升转矩，此外，永磁体与绕组分开放置也进一步提升了永磁电机的内腔利用率以及方便永磁体的散热[1-2]。

永磁电机气隙磁场计算是电机电磁设计和性能优化的基础，目前，针对永磁电机气隙磁场的计算方法主要有等效磁路法、解析法和有限元法，然而等效磁路法过分依赖于经验系数对结果的修正[3-5]，而修正系数与电机众多形状参数有关，使得修正系数难以准确得到，最终求出的气隙磁密也不够精确；有限元法计算精度高，且能够计算任意复杂边界条件下的磁场分布，但是其建模和计算的时间太过冗长，在电机的优化设计中并不方便[6]；相比之下，解析法物理概念清晰，求解速度快、计算量小、参数调整方便，且有利于电机各方面性能的分析和改进[7]。

在电机解析模型的分析中，随着电机边界条件的复杂度提升，其解析求解的复杂度也随之提升。文献[8]最早提出在极坐标系下采用标量磁位求解无槽表贴式径向充磁永磁无刷电机的气隙磁场分布。定子或转子电枢开槽后，会使磁场求解域边界变得更加复杂，针对电枢开槽后的气隙磁场求解问题，文献[9]采用保角变换，求得电枢开槽时的相对气隙磁导函数，并与无槽时的气隙磁场相乘，可以得出开槽后的气隙磁场分布，但该方法只能求解开槽后的径向磁场分布，而无法求出开槽切向磁场分布，从而无法准确求出电磁转矩；文献[10]引入复磁导函数，能够准确求出开槽效果对气隙磁场径向和切向的影响，但是该复数磁导函数为一非线性复函数，求解过程复杂，且采用的是无限槽深单槽模型，无法考虑槽与槽之间的影响；文献[11]采用子域模型法，将电机气隙磁场求解域划分为永磁体域、气隙域和槽域，分别求解各个子域的拉普拉斯方程或泊松方程，并利用傅里叶级数将不同求解域的边界条件耦合起来，该方法能够考虑槽深对气隙磁场的影响。文献[12]提出了针对磁齿轮气隙磁场的矢量磁位子域模型，相较于传统电机，磁齿轮的转子是由镂空的调制块组成，且具有内外两层气隙，其边界条件更加复杂，增加了求解复杂度，但是该模型未考虑实际的永磁体回复磁导率。

双定子磁通反向电机的边界条件十分复杂，其具有磁齿轮的转子调制块结构，同时定子电枢上又开有齿槽，传统计及齿槽效果的保角变换法已经不再适用。本文将建立双定子磁通反向电机的精确子域模型，考虑其转子调制块以及外定子开槽的双重效果对内外气隙磁场的影响，同时考虑永磁体的相对回复磁导率，将求解域划分为永磁体、内气隙、转子调制块气隙、外气隙和外定子槽共5个求解子域，在每个子域分别求解矢量拉普拉斯方程或泊松方程，并根据边界条件耦合各个子域磁矢位方程，采用直接解析法求解出空载气隙磁场分布。以一台12/10极的双定子磁通反向电机模型作为算例，进行磁场求解，并与有限元结果相比较，验证了本文模型推导的正确性与该方法的准确性。

1 DS-FRM的磁场解析模型

本文以12/10极的双定子磁通反向电机为例进行磁场解析计算，其二维截面图如图1所示。磁通反向电机属于磁场调制电机[13]的一种，通过转子调制块的旋转，对磁场进行调制，对于不同类型的磁场调制电机，都具有共同的运行规则[1]：

θe=Q·θm

(1)

(2)

式中，θe和θm分别为转子位置的电角度和机械角度，Q为转子调制块个数，n为转速，f为频率。

1.1 基本假设

为了便于分析，做出如下假设：

1)内、外定子和转子调制块的磁导率为无穷大；

2)永磁体的相对回复磁导率取其实际回复磁导率值；

3)定子槽为径向直槽，槽内无电流；

4)计算场域为二维场，忽略端部效应。

图1 双定子磁通反向电机横截面示意图

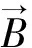
在空气区域，

(3)

在永磁体区域，

(4)

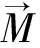
极坐标下，磁感应强度为

(5)

(6)

式中，A为矢量磁位。

将二维极坐标(r,θ)固定到定子上，以第i个转子调制块气隙和第z个外定子槽的中心作为模型的初始位置，则第i个转子调制块气隙和第z个外定子槽的的初始位置定义为

(7)

(8)

式中，θr0为转子调制块的初始位置，θz0为外定子槽的初始位置。

为了便于各子域通解的表达和积分常数的求解，定义两个函数[13]：

(9)

(10)

双定子磁通反向电机的磁场求解域可划分为5个求解子域：永磁体、内气隙、转子调制块气隙、外气隙、外定子槽。以矢量磁位A作为二维偏微分方程在极坐标下的求解变量，则有：

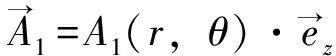
(11)

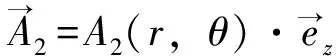
(12)

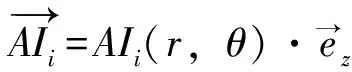
(13)

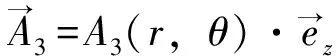
(14)

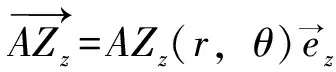
(15)

1.2 永磁体子域通解

永磁体子域的泊松方程如下：

(16)

式中，Mr为永磁体径向极化强度，Mθ为永磁体切向极化强度。

对于径向充磁的永磁体来说：

(17)

其中，

(18)

式中，Br为永磁体剩磁密度，p为永磁体极对数，φi为永磁体N极中心位置角。

永磁体子域的边界条件为

(19)

由边界条件可得，永磁体子域的泊松方程的通解为[14]

(20)

式中，a1(n)、c1(n)为永磁体子域的积分常数；n为永磁体子域磁场谐波次数；Xr(n)为与永磁体子域泊松方程特解相关的级数项，由永磁体极化强度决定，Xr(n)可表示为

(21)

其中，

(22)

1.3 内、外气隙子域通解

内气隙子域的拉普拉斯方程如下：

(23)

内气隙子域边界条件为

(24)

其中，

(25)

由边界条件可得，内气隙子域的通解为

(26)

式中，a2(n)、c2(n)、b2(n)、d2(n)为内气隙子域的积分常数；n为内气隙子域磁场谐波次数。

外气隙子域拉普拉斯方程如下：

(27)

外气隙子域边界条件为

(28)

其中，

(29)

(30)

由边界条件可得，外气隙子域的通解为

(31)

式中，a3(n)、c3(n)为外气隙子域的积分常数；n为外气隙子域磁场谐波次数。

1.4 转子调制块气隙子域通解

对第i个转子调制块气隙子域，如图2所示,其子域拉普拉斯方程为

(32)

其边界条件为

(33)

由边界条件可得，第i个转子调制块气隙的子域通解为

(34)

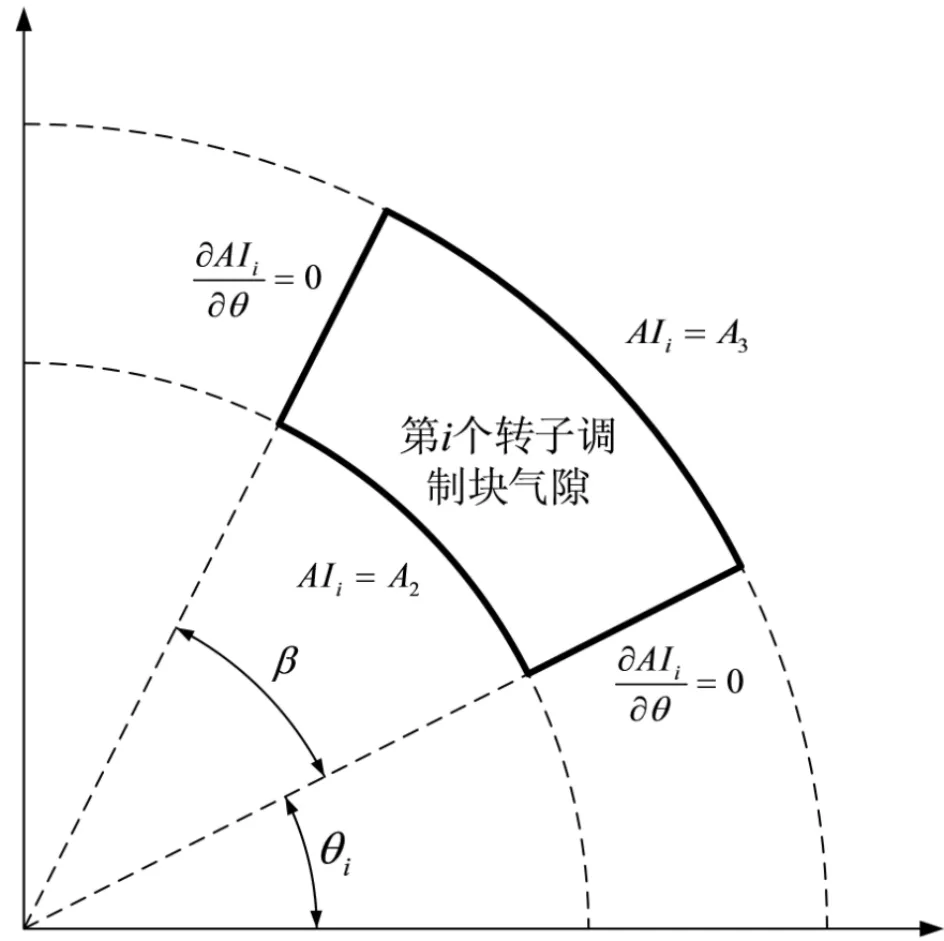
图2 第i个转子调制块气隙及其边界条件

其中，a0(i)、b0(i)、si(k)、ti(k)为转子调制块气隙子域的谐波系数，k为转子调制块气隙子域磁场谐波次数。

1.5 外定子槽子域通解

对于外定子槽子域，如图3所示，外定子槽子域的拉普拉斯方程为

(35)

其边界条件为

(36)

由边界条件可得，第z个外定子槽子域的通解为

(37)

式中，u0(z)、uz(k)为外定子槽子域的谐波系数，k为外定子槽子域磁场谐波次数。

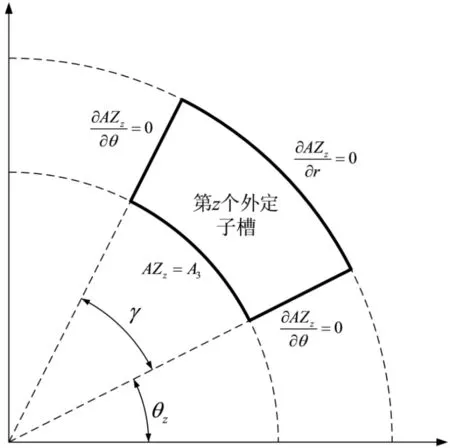
图3 第z个外定子槽及其边界条件

2 积分常数的确定

在得到5个子域通解的情况下，可以根据相关边界条件得出积分常数。

2.1 永磁体子域积分常数的确定

根据边界条件(19)，结合式(20)、式(26)可得：

(38)

(39)

2.2 内气隙子域积分常数的确定

根据边界条件(24)，结合式(20)、式(26)可得：

(40)

(41)

(42)

(43)

2.3 转子调制块气隙子域积分常数的确定

根据边界条件(33)，结合式(34)、式(36)可得：

(44)

(45)

(46)

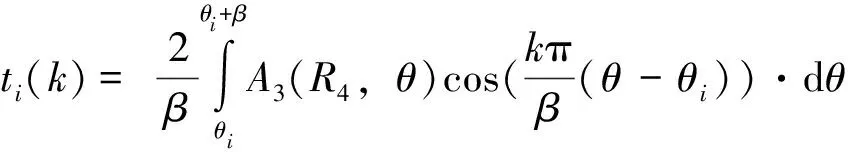
(47)

2.4 外气隙子域积分常数的确定

根据边界条件(28)，结合式(31)、式(34)可得：

(48)

(49)

(50)

(51)

2.5 外定子槽子域积分常数的确定

根据边界条件(36)，结合式(37)、式(31)可得：

(52)

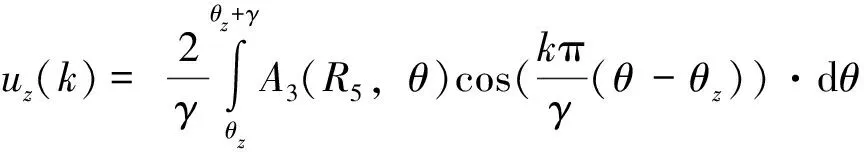
(53)

积分常数的推导和求解过程见附录A。

3 磁场计算和有限元验证

3.1 样机参数

本文以一台径向充磁双定子磁通反向电机为例，样机参数如表1所示。

表1 双定子磁通反向电机样机参数

3.2 气隙磁密分布

根据附录A的计算结果，可以得到内外气隙的磁矢位系数。取内气隙计算半径rig=26.25mm，则由式(5)、式(6)和式(31)可得，内气隙的径向磁密和切向磁密分别为

(54)

(55)

同理，取外气隙计算半径rog=30.75 mm，可由式(5)、式(6)和式(31)可得，外气隙的径向磁密和切向磁密分别为：

(56)

(57)

图4和图5分别给出了双定子磁通反向电机的内气隙和外气隙磁密分布，可以观察到对于内外两层气隙，解析结果和有限元结果几乎完全吻合。

图4 内层磁密分布

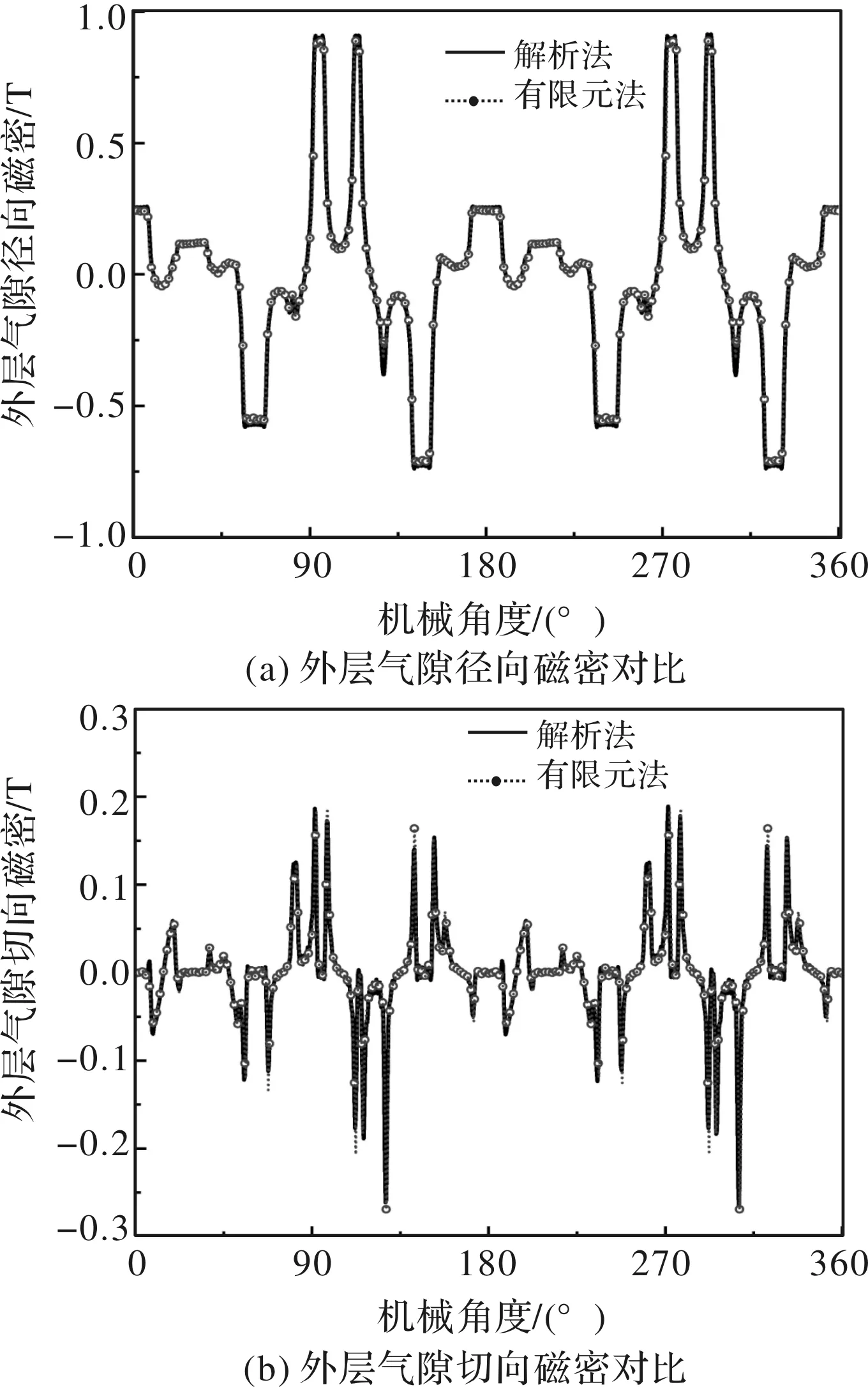
图5 外层磁密分布

3.3 齿槽转矩

根据文献[14]，麦克斯韦张量法是计算电机齿槽转矩的有效方法,其基本思路是在磁场中把一定体积上的体积力转换为一组在体表面的张力进行计算。当永磁电机转子和定子相对静止时，系统处于一个平衡状态，而当两者的相对位置发生变化时，平衡被破坏，转子将受到趋于保持在原平衡位置的切向磁拉力的影响，形成一个永磁体与铁心相互作用的脉动转矩，即所谓的齿槽转矩：

(58)

式中，L为电机的轴向长度，rig、rog为内外气隙磁场的测量半径，B2r、B2t和B3r、B3t分别为内外气隙测量半径处的径向磁密和切向磁密。

齿槽转矩在整个周期内的波动次数为

T=LCD(2p,Q)

(59)

对于12/10的双定子磁通反向电机来说，由式可以计算出其齿槽转矩的波动次数T=60,因此，在一个电周期内，其齿槽转矩的波动次数为T/Q=6次。

图6给出了双定子磁通反向电机在一个电周期内的齿槽转矩分布，可以看出解析结果和有限元结果吻合度较高且波动次数与计算结果一致，子域模型法求得的齿槽转矩幅值为334 mNm，有限元法求得的齿槽转矩幅值为347 mNm，误差为3.7%，进一步验证了解析模型的准确性。

图6 齿槽转矩对比

4 结 论

本文基于精确子域模型法建立了一种求解具有双层气隙、复杂边界条件的双定子磁通反向电机的空载磁场解析方法，通过解析计算其空载磁场的气隙磁密分布，并与有限元结果对比，验证了该解析方法的准确性。在此基础上，采用麦克斯韦张量法进行齿槽转矩的解析求解，与有限元法的结果吻合较好，从而为双定子磁通反向电机的设计和优化奠定了良好的基础。