高速内置式永磁同步电机转子强度分析

顾雪政，顾海勤，倪红军，吕帅帅，石启军

(1. 南通大学，江苏 南通 226019；2. 南通科技职业学院,江苏 南通 226019)

0 引 言

高速永磁同步电机有着能耗低、体积小、功率密度高的优点，被广泛应用于储能飞轮、高速泵、压缩机等工业领域[1-4]。永磁同步电机按转子的磁路结构可划分为表贴式和内置式。相较于表贴式，内置式永磁同步电机转子冲片结构简单有助于高速永磁同步电机的产业化生产，且其 轴与 轴磁路的电抗不相等，有利于提升电机的运行转速[5]。

目前，对转子冲片结构的研究已经成为高速永磁同步电机研究领域的热点之一。表贴式永磁同步电机一般会在永磁材料表面加设一保护套来避免应力对永磁材料的损伤[6]。但是，电机高速运行时供电频率高，保护套表面会产生额外的涡流损耗，导致电机效率降低[7-8]。内置式永磁同步电机高速运行时产生的离心应力由转子冲片上的隔磁桥承担。增大隔磁桥的厚度可提高转子冲片的机械强度但其空载漏磁系数也相应增加，从而影响电机的电磁性能[9]。文献[10]基于受力平衡原理推导出了内置式一型永磁同步电机转子隔磁桥最大应力的解析公式，并根据有限元法证明了该解析公式的正确性。文献[11]提出了在内置式一型永磁同步电机转子冲片上增设加强筋的方法，并通过有限元法验证了该方法的可行性，但没有深入分析增设的加强筋对电机电气性能的影响。

基于离心力产生的原理对高速内置式V型永磁同步电机转子冲片的受力情况进行了研究。首先，建立了高转速下转子冲片最大应力的数学表达式，通过有限元仿真软件验证了此表达式的准确性；然后，对V型结构每条边的永磁体进行了分段处理，通过分段桥来分担隔磁桥上的应力，以此降低高转速下电机转子隔磁桥处的离心力；最后，依据有限元仿真软件分析了分段桥数量对电机机械强度及电气性能的影响，并给出了实例电机15 000 r/min转速下转子冲片结构的最优设计。

1 转子冲片的应力分析

相较于内置式一型永磁同步电机，内置式V型永磁同步电机的凸极效应更加明显，更有利于电机的弱磁调速及高速运行[12]，内置式V型永磁同步电机转子冲片的结构如图1所示。

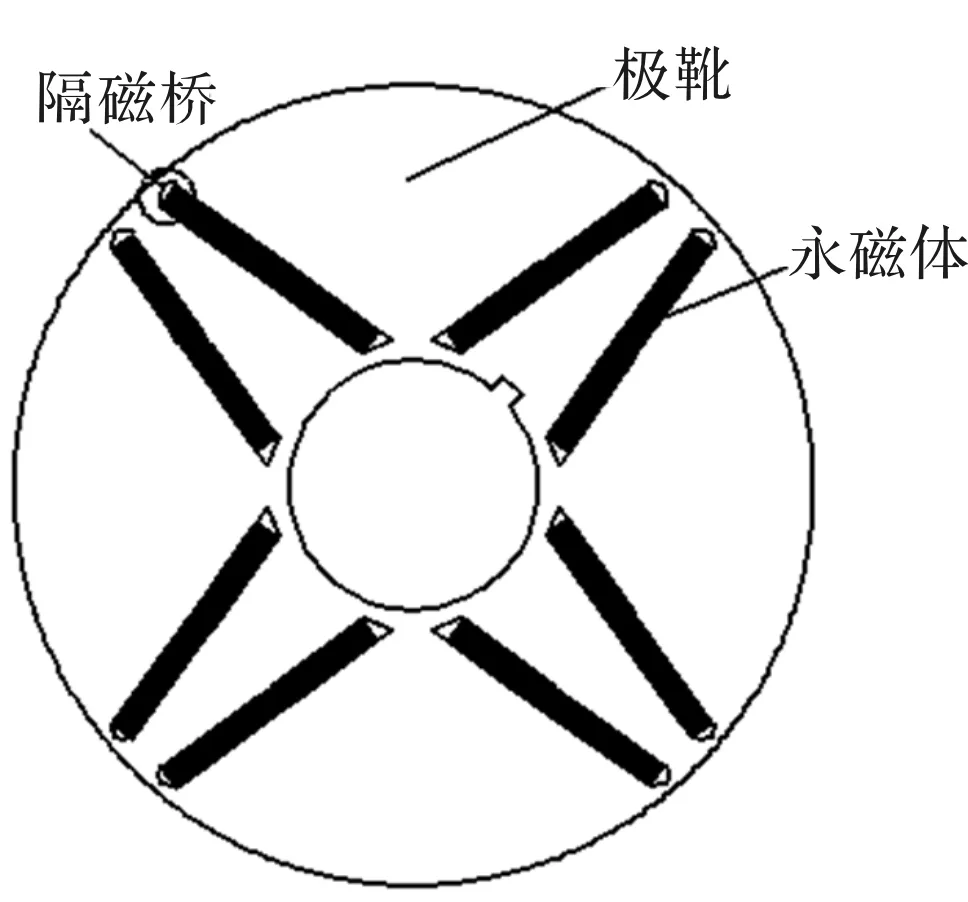
图1 V型内置式转子冲片结构

离心力、电磁力、温度及振动均会对内置式永磁同步电机转子的机械强度产生影响，但在高速运行阶段，相较于高速离心力的大小，可忽略后三个因素对其强度的影响[13]。

内置式永磁同步电机高速运行时，隔磁桥处同时承受着极靴和永磁体引起的离心力，隔磁桥处的离心应力即为转子冲片所受最大应力[14]。因此，分别计算出极靴和永磁体产生的离心力便可推得转子冲片的最大应力。

由于离心力的大小与离心半径成正比，为了计算出极靴及永磁体产生的离心力，需要先求出两者的等效离心半径(求解极靴及永磁体的质心坐标)。

对于任意形状的几何物体，其质心坐标的方程可表示为

(1)

式中,M为物体的质量；μ(x,y,z)为单位体积的密度函数；x、y、z为三维坐标；dv为单位体积。

本文研究的高速转子其质量沿轴向是均匀分布的，可以将求解三维模型质心的问题转变为求解二维模型质心的问题。同时考虑到极靴和永磁体的密度是均匀分布的，因此式(1)可以简化为

(2)

式中,A为闭合区域的面积；ds为单位面积。

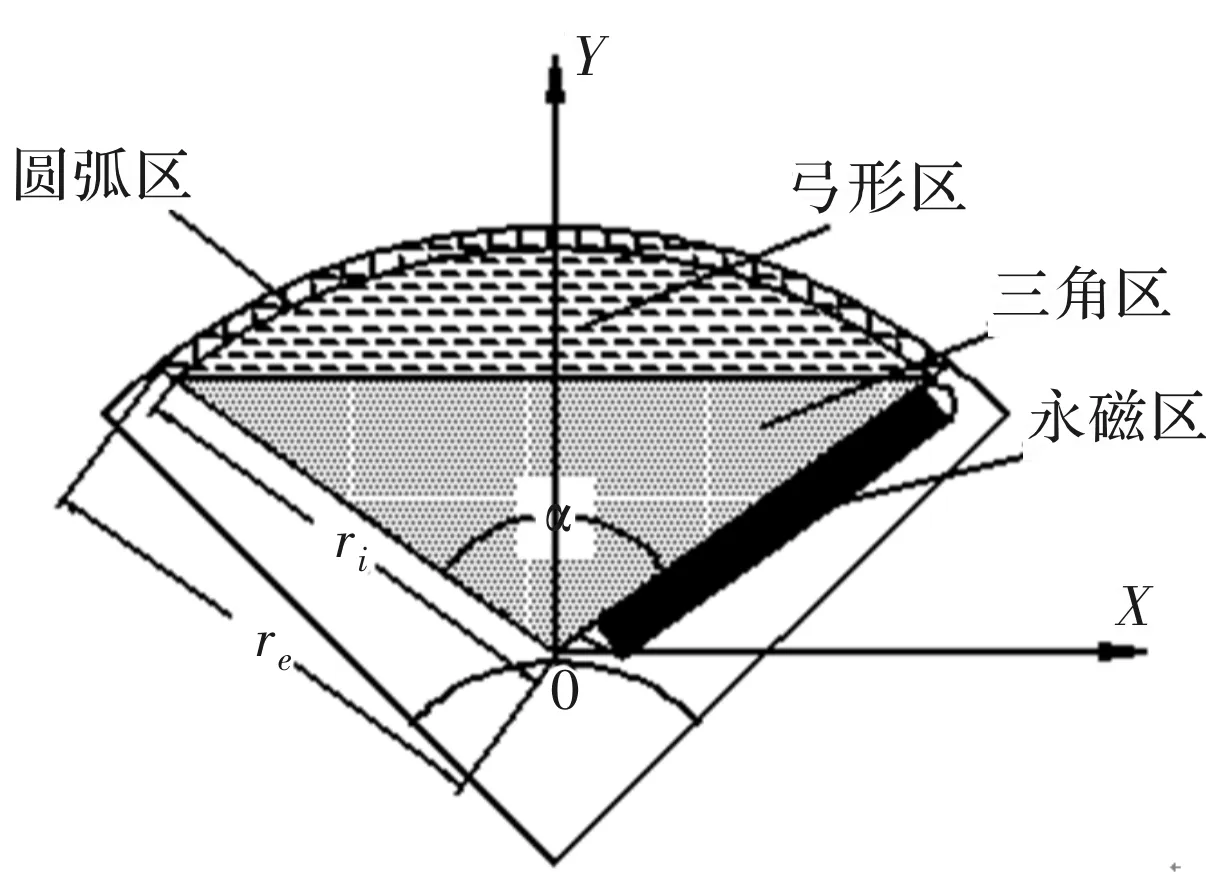
图2 转子区域划分

由式(2)推得极靴的质心坐标表示为

(3)

式中,A1、A2、A3分别为圆弧区、弓形区以及三角区的面积。

圆弧区的面积及其在 轴方向积分为

(4)

式中,re、ri分别为圆弧的外径和内径；α为永磁体间的夹角。

同理利用弓形及三角形质心坐标的求解方法，可以推得弓形及三角区面积及其在Y轴方向的积分，如式(5)和式(6)所示：

(5)

(6)

由式(2)推得永磁体的质心坐标为

(7)

式中,A4为永磁体的面积。

永磁区面积及其在r轴方向的积分表示为

(8)

式中,hpm、bpm分别为永磁体的厚度和宽度。

依据离心力的计算公式以及求解得到的质心坐标即可得到极靴与永磁体产生的离心力：

(9)

式中,mFe、mpm分别为极靴和永磁体的质量；ω为转子的机械角速度。

分析转子冲片的结构可知，隔磁桥处所受离心力为极靴和永磁体合力的径向分量，因此转子冲片最大应力表示为

(10)

式中,b为隔磁桥的宽度；l为转子的铁心长度。

2 试验样机转子强度的计算与仿真

样机电压为380 V，最高转速为15000 r/min，最高电源频率为500 Hz。为降低电机高频下的铁心损耗[15]，选取宝钢无取向电工钢B35A250作为定转子铁心的材料。为保证永磁材料具有足够的剩磁、矫顽力及最大磁能积，选用钕铁硼做为永磁体材料。电工钢B35A250及钕铁硼的材料特性如表1所示。

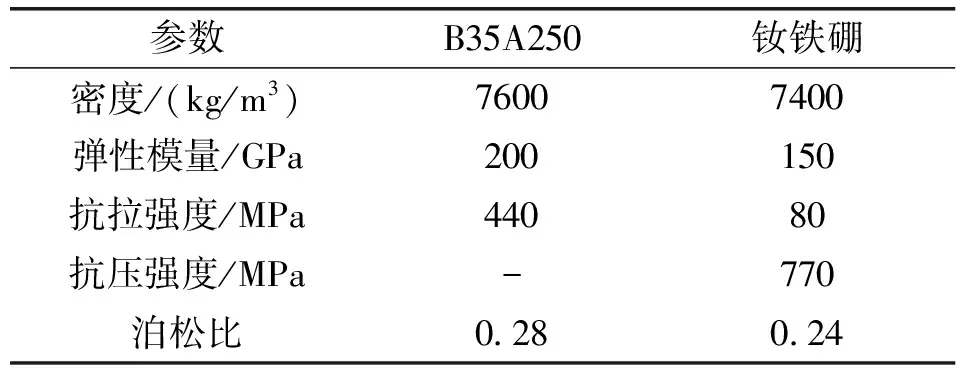
表1 转子材料特性

电机转子冲片的主要结构参数为：转子冲片内外径分别为56 mm和140 mm；永磁体宽为45 mm，厚度为8 mm；隔磁桥平均厚度为5.12 mm，平均宽度为2.35 mm。

利用上述解析方法结合转子的结构参数及其材料特性计算出不同转速下转子冲片的最大应力，同时在有限元软件中模拟出对应转速下转子冲片的应力分布情况，以验证解析法的准确性。两种方法下的结果对比如图3所示。

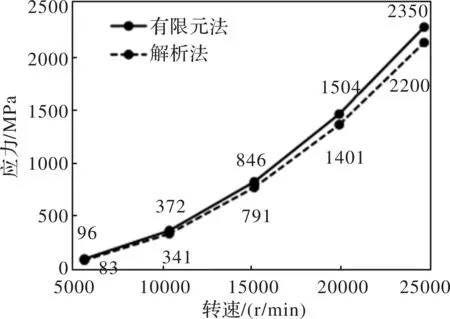
图3 解析法与有限元法结果对比

由图3可知：不同转速下，解析法计算得到的最大应力稍小于有限元的仿真结果，这是因为公式推导时划分了一近似三角形区域，解析计算时也简化了隔磁桥处的局部细节尺寸，但两种方法的计算结果较为接近，最大误差不超过7%。结果证明，解析法完全能够用于转子结构的优化设计。

当电机转速为15000 r/min时，转子冲片的最大应力为846.5 MPa，此时应力分布如图4所示。但是，电工钢B35A250的屈服强度仅为440 MPa，需要采取必要措施降低隔磁桥处的应力。

图4 15000r/min下转子冲片应力分布

3 转子机械强度的优化

为降低电机转子冲片的最大应力，对永磁体V型结构的每条边进行分段，将隔磁桥处的应力分散到分段桥上。永磁体分段后的转子冲片结构如图5所示。

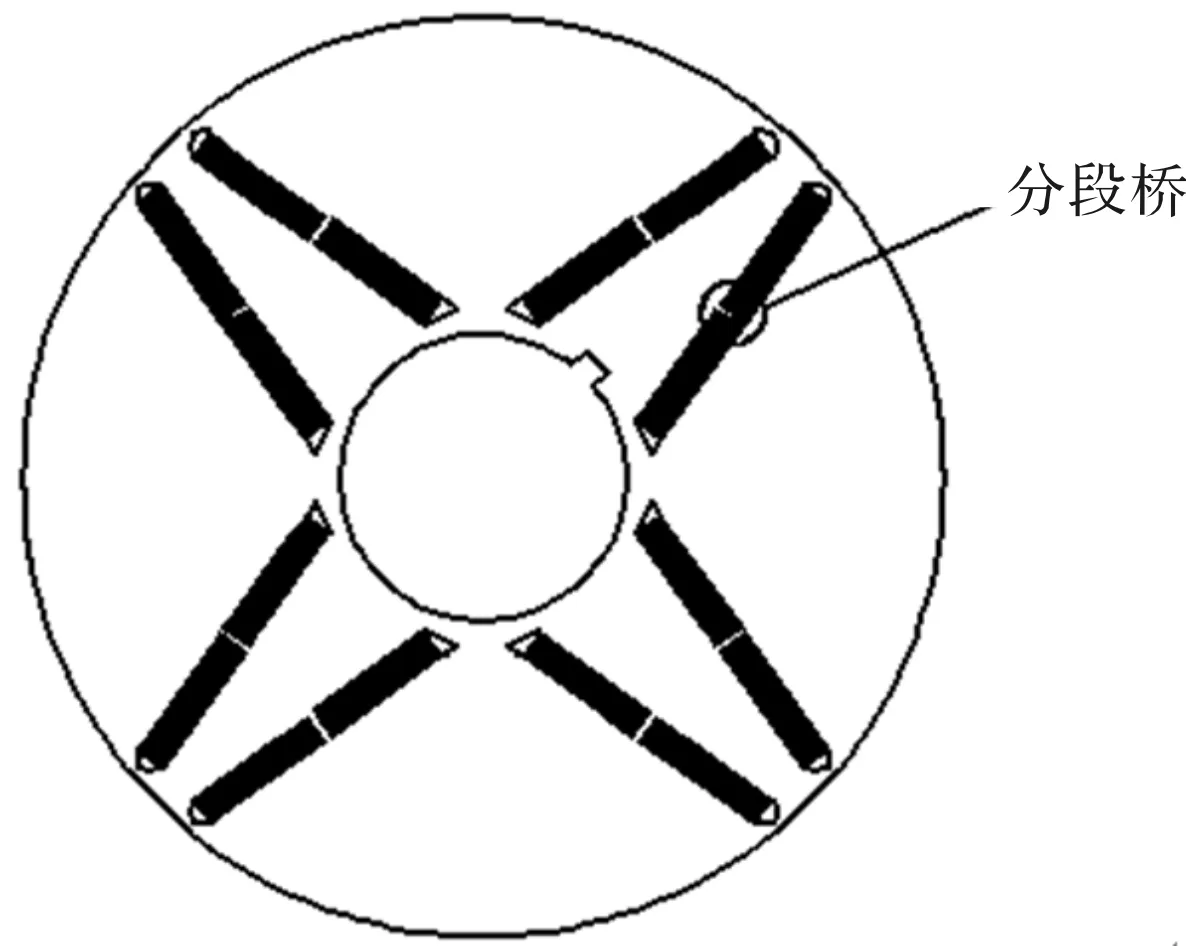
图5 永磁体分段转子冲片结构

将永磁体的每条边均匀分成两段，分段桥的宽度w为3 mm，转子冲片应力分布如图6所示。对比图4与图6可知，永磁体分段后，转子冲片的最大应力降到403.71 MPa，分段桥有效分担了隔磁桥处的应力，机械强度得到了显著的提高。

图6 两段永磁体转子冲片应力分布

永磁体分两段后，转子冲片的最大应力虽然小于电工钢的抗拉极限但安全裕量较小，仍然无法满足实际工程的需要。为此可将永磁体每条边重新均分为三段，分段桥的宽度为2 mm，得到如图7所示的应力分布云图。结果显示，永磁体分成三段后，转子冲片的最大应力仅为317.53 MPa，转子冲片的机械强度得到了进一步加强。

图7 三段永磁体转子冲片应力分布

4 分段桥对电机电气性能的影响

空载漏磁系数σ0是永磁同步电机的一个非常重要的参数，过大的空载漏磁系数会对电机的空载反电动势E0、效率等电气性能产生影响[16]。为分析分段桥对电机空载漏磁系数的影响，利用电磁软件Ansoft Maxwell对三种结构下电机的磁力线分布情况进行模拟仿真。由仿真结果可知，分段桥处存在着闭环的漏磁路，随着分段桥数量的增加，电机的空载漏变大。图8为永磁体分两段时电机磁力线的分布云图。

图8 两段永磁体电机磁力线分布

依据磁力线仿真结果，计算得到了分段桥数量与电机空载性能之间的关系，如表2所示。

表2 不同分段桥数量下电机空载性能

通过对比可知，随着分段桥数量的增加空载漏磁系数逐渐增大、空载反电动势逐渐减小，而机械强度却逐步提高。当用2个分段桥将永磁体分成三段时，电机的空载反电动势为339.4 V，空载反电动势与电机额定电压之比为0.89:1，转子冲片的最大应力仅为317.53 MPa。综合考虑电机的机械强度及电气性能，选用2个分段桥将永磁体分成三段的转子结构为实例电机的最佳方案。

5 结 语

本文以内置式V型永磁同步电机的转子结构为研究对象，对转子冲片的机械强度进行了分析计算。为了提高转子冲片的机械强度，提出了对永磁体沿径向分段的结构优化方案，并利用有限元仿真软件进行了验证，得到了以下结论：

(1)隔磁桥处的离心应力即为转子冲片所受最大应力，基于离心力产生的原理推导得到了最大应力的数学表达式并通过有限元法验证了解析法的准确性；

(2)分段桥可有效分担转子隔磁桥处的离心应力，转子冲片的机械强度随着分段桥数量的增加得到了显著提高；

(3)随着分段桥数量的增多，电机空载漏磁系数变大，空载反电动势变小，因此，在满足机械强度的前提下应尽量减少分段桥的数量；

(4)本文的研究方法不局限于实例电机，可为同类永磁同步电机转子结构的优化设计提供参考。