非线性时间分数阶Klein-Gordon方程的精确行波解①

张练，刘小华，曾职云

贵州民族大学 数据科学与信息工程学院， 贵阳 550025

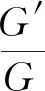
(1)

的精确行波解， 其中β，γ是任意非零常数．

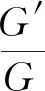
1 方程(1)有界行波解的存在性

对(1+1)维非线性时间分数阶Klein-Gordon方程(1)做如下的分数复变换[15]

(2)

其中l，λ是任意非零常数， Γ为伽马函数， 则可将方程(1)转化为方程

(3)

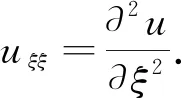
(4)

对系统(4)进行首次积分

(5)

再令

f(u)=βu+γu3=0

(6)

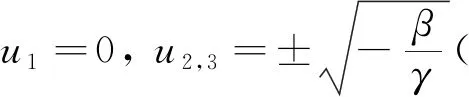
(7)

根据平面动力系统理论[16-17]可知， 如果J(ui， 0)<0则为鞍点， 如果J(ui， 0)>0则为中心， 如果J(ui， 0)=0则为尖点， 因此对于系统(4)有：

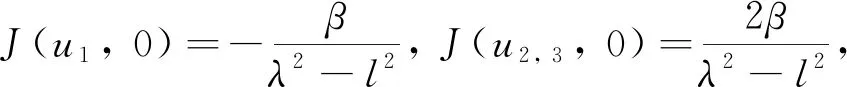
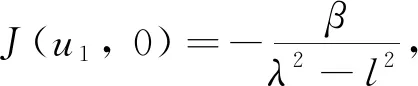
3) 当βγ<0，λ2-l2<0时， 平衡点(u1， 0)， (u2， 3， 0)对应的Jacobi矩阵行列式分别为

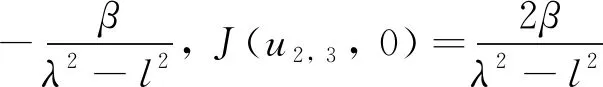
从而可知平衡点(u1， 0)在β>0时为中心， 在β<0时为鞍点； 平衡点(u2， 3， 0)在β>0时为鞍点， 在β<0时为中心．

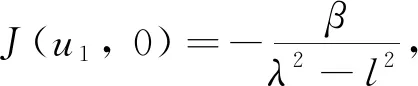
根据上面的奇点分析， 利用Maple软件画出系统(4)在不同参数条件下的相图见图1．

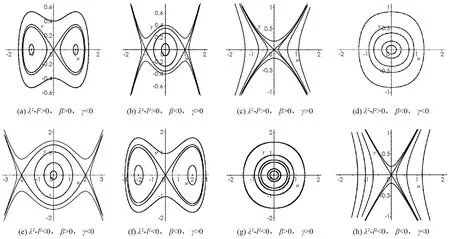
图1 系统(4)在不同参数条件下的相图

由平面动力系统理论与方法[16-17]可知， 同宿轨对应着方程(3)的钟状孤波解， 异宿轨对应着方程(3)的扭状孤波解， 闭轨对应着方程(3)的周期解． 因此根据相图1中的(a)-(h)， 可得出方程(3)的有界行波解的个数及存在性结论为：

1) 系统(4)在λ2-l2>0，β>0，γ<0时存在两条同宿轨， 无穷多个闭轨， 从而方程(3)存在两个钟状孤波解和无穷多个周期解(图1(a))．

2) 系统(4)在λ2-l2>0，β<0，γ>0时存在两条异宿轨， 无穷多个闭轨， 从而方程(3)存在两个扭状孤波解和无穷多个周期解(图1(b))．

3) 系统(4)在λ2-l2>0，β>0，γ>0时不存在闭轨(图1(c))．

4) 系统(4)在λ2-l2>0，β<0，γ<0时存在无穷多个闭轨， 从而方程(3)存在无穷多个周期解(图1(d))．

5) 系统(4)在λ2-l2<0，β>0，γ<0时存在两条异宿轨， 无穷多个闭轨， 从而方程(3)存在两个扭状孤波解和无穷多个周期解(图1(e))．

6) 系统(4)在λ2-l2<0，β<0，γ>0时存在两条同宿轨， 无穷多个闭轨， 从而方程(3)存在两个钟状孤波解和无穷多个周期解(图1(f))．

7) 系统(4)在λ2-l2<0，β>0，γ>0时存在无穷多个闭轨， 从而方程(3)存在无穷多个周期解(图1(g))．

8) 系统(4)在λ2-l2<0，β<0，γ<0时不存在闭轨(图1(h))．

由上面的定性分析可知， 方程(3)存在4个钟状孤波解、 4个扭状孤波解和无穷多个周期波解， 下面运用辅助方程法讨论方程(1)的一些有界行波解的精确表达式．

2 辅助方程法

运用辅助方程法求解非线性发展方程的精确解是十分有效的， 本文运用的辅助方程法是Khater博士在2018年所提出并改进的， 辅助方程法的具体步骤如下[9-10]：

考虑如下的非线性偏微分方程：

P(u，ut，ux，utt，uxx，uxt， …)=0

(8)

其中u(x，t)是未知函数， 且P是包含u(x，t)及其各导数的多项式函数．

步骤1： 对方程(8)做行波变换u(x，t)=u(ξ)，ξ=lx-λt， 其中l，λ是任意非零常数， 即方程(8)可化为如下的常微分方程：

F(u， -λu′，lu′，λ2u″，l2u″， -λlu″， …)=0

(9)

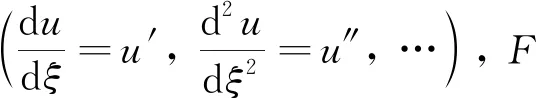
步骤2： 假设常微分方程(9)的解具有如下形式：

(10)

其中ai，bi(i=0，1，2，…，n)为待定系数，n由齐次平衡原则确定，f(ξ)满足如下常微分方程

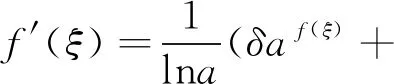
(11)

其中α，ϑ，δ，a是非零常数且a>0，a≠1．

步骤3： 将方程(10)，(11)代入方程(9)， 合并a±if(ξ)，i=0，1，2，…，n的各次幂系数， 并令各次幂系数等于零， 得到关于a0，ai，bi，l，λ(i=1，2，…，n)的代数方程组， 结合Maple软件求解代数方程组， 可得a0，ai，bi，l，λ(i=1，2，…，n)的值．

步骤4： 通过方程(11)的解和步骤3的值， 由假设(10)得出方程(9)的解， 进而可获得方程(8)行波解的精确表达式．

方程(11)的解有如下3种情形：

情形1： 如果ϑ2-4αδ>0且δ≠0， 那么有

(12)

情形2： 如果ϑ2-4αδ<0且δ≠0， 那么有

(13)

情形3： 如果ϑ2=4αδ且δ≠0， 那么有

(14)

3 方程(1)行波解的精确表达式

下面利用辅助方程法来讨论方程(1)的有界行波解， 通过该方法得出了方程(1)的两组不同参数的解， 则具体根据方程(3)的最高阶导数项u″(ξ)与最高阶非线性项u3(ξ)的平衡原则， 有n+2=3n得n=1， 根据上述方法可设方程(3)的解具有如下形式：

u(ξ)=a0+a1af(ξ)+b1a-f(ξ)

(15)

其中：a0，a1，b1为待定系数； 将方程(15)及其导数代入方程(3)， 合并a±if(ξ)，i=0，1，2，3的各次幂， 并令各次幂的系数等于零， 得到关于a0，a1，b1，l，λ的代数方程组为：

(16)

结合Maple软件求解方程组(16)， 得出以下两种情形．

情形1：

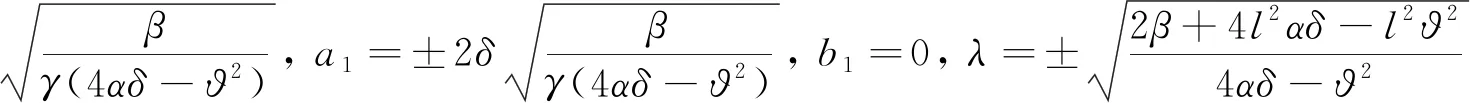
(17)

其中l为任意非零常数．

情形2：

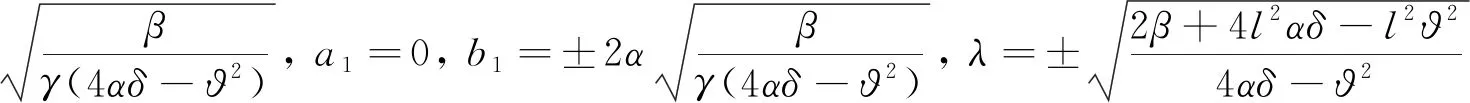
(18)

其中l为任意非零常数．

由(15)，(17)式与方程(11)的解(13)、 分数复变换(2)可得方程(1)的有界行波解为：

(19)

(20)

其中ϑ2-4αδ<0且δ≠0，l为任意非零常数．

由(15)，(17)式与方程(11)的解(12)、 分数复变换(2)可得方程(1)的有界行波解为：

(21)

(22)

其中ϑ2-4αδ>0且δ≠0，l为任意非零常数．

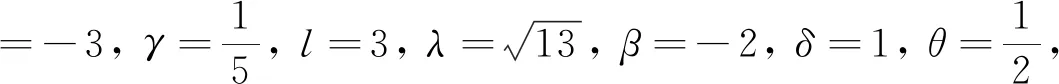
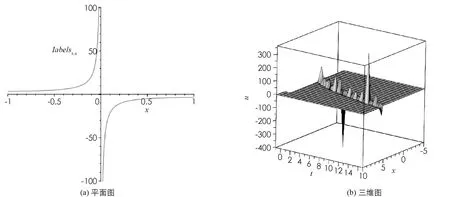
图2 解u7

由(15)，(18)式与方程(11)的解(13)、 分数复变换(2)可得方程(1)的有界行波解为

(23)

(24)

其中ϑ2-4αδ<0且δ≠0，l为任意非零常数．

由(15)，(18)式与方程(11)的解(12)、 分数复变换(2)可得方程(1)的有界行波解为

(25)

(26)

其中ϑ2-4αδ>0且δ≠0，l为任意非零常数．

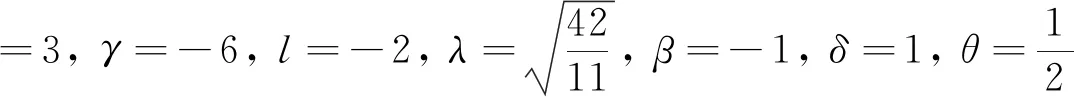
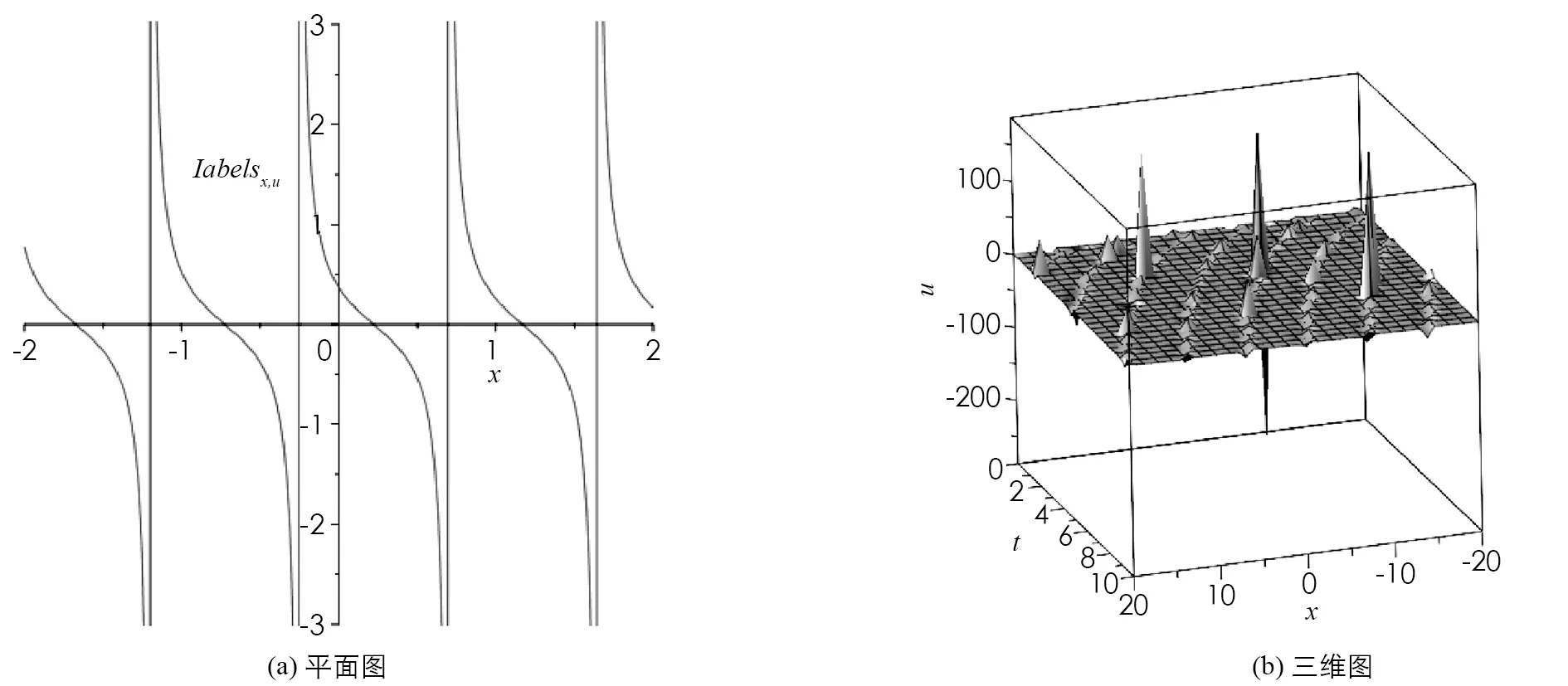
图3 解u11

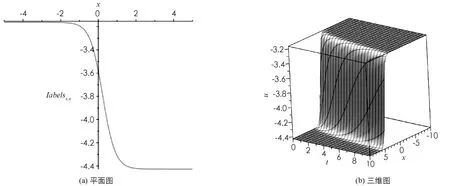
图4 解u14

注1解(25)与解(21) 分别是图1(b)中的两条异宿轨对应的扭状孤波解的两种不同表达式， 解(26)与解(22)分别是图1(e)中的两条异宿轨对应的扭状孤波解的两种不同表达式．

4 结论

本文利用平面动力系统理论与方法以及辅助方程法， 讨论了非线性时间分数阶Klein-Gordon方程有界行波解的存在性及精确表达式， 其中包括双曲函数解、 三角函数解； 由定性结论可知方程(1)还存在4个钟状孤波解和无穷多个周期解， 在此用辅助方程法还没能给出其精确表达式．