解非线性半定规划的一种回溯线搜索型算法①
李丹丹,王松华,李远飞
1.广州华商学院 应用数学系, 广州 511300;2.百色学院 数学与统计学院, 广西 百色 533000
考虑如下非线性半定规划问题(NLSDP):
(1)

线性半定规划[1-2]是优化领域中最经典的问题, 然而众多实际问题属于非线性半定规划问题, 如工程设计、 最优控制、 经济、 金融等领域[3-4]. 因此, 非线性半定规划的研究具有理论创新和实际应用的意义. 若干有效方法可求解非线性半定规划问题且其效果显著, 如增广拉格朗日方法[5]、 序列半定规划方法[6]、 序列线性方程组方法[7]、 乘子法[8]、 原始-对偶内点法[9], 其中序列半定规划方法应用较广. 很多学者将优良的非线性规划算法推广到非线性半定规划问题中, 如文献[10]借鉴传统非线性规划的子问题修正技术, 并结合信赖域框架, 提出了求解非线性半定规划的一个无可行性恢复阶段的滤子算法. 文献[11]采用非单调线搜索技术来保证目标函数或约束违反度函数的充分下降, 从而提出一个求解非线性半定规划的无罚无滤序列二次半定规划算法. 文献[12]提出一个求解带有不等式约束的非线性规划全局收敛性算法, 该算法的接受准则既不使用罚函数也不使用滤子, 且效果显著. 本文在文献[12]的基础上, 将该思想推广到非线性半定规划中, 提出一个求解非线性半定规划问题的无罚函数无滤子回溯线搜索型序列半定规划算法.
1 算法描述
二阶连续可微函数f(x)的梯度和Hesse矩阵分别记为f(x)和2f(x). 二阶连续可微向量函数h(x): =(h1(x),h2(x), …,hp(x))T, 则称矩阵Dh(x)=(h1(x),h2(x), …,hp(x))T∈Rp×n为h(x) 的雅可比矩阵. 二阶连续可微矩阵函数G(x), 记其微分算子DG(x)为
且对任意的d∈Rn
记其伴随算子DG(x)*为
其中Z∈Sm.
记NLSDP(1)的拉格朗日函数为
L(x,λ,Y)=f(x)+λTh(x)+〈Y,G(x)〉
其中x∈Rn,λ∈Rp,Y∈Sm.
定义1若x*∈Rn是NLSDP(1)的可行点, 且存在向量λ*∈Rp和矩阵Y*∈Sm满足如下条件:
xL(x*,λ*,Y*)=f(x*)+Dh(x*)Tλ*+DG(x*)*Y*=0
h(x*)=0,G(x*)⪯0,Y*0, 〈G(x*),Y*〉=0
则称(x*,λ*,Y*)是NLSDP(1)的一个KKT点对, (λ*,Y*)是在x*处相对应的拉格朗日乘子.
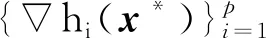
本文采用线搜索型序列半定规划方法框架, 设当前迭代点为xk∈Rn, 定义产生搜索方向的二次半定子问题QSD(xk,Bk) 如下:
(2)
其中矩阵Bk∈Rn×n是NLSDP(1)的拉格朗日函数的Hesse阵或其近似阵. 若QSD(xk,Bk)存在最优解, 则记其解为dk. 同时, 为了度量NLSDP(1)的约束可行性, 下面给出其约束违反度函数的定义:
θ(x)=λ1(G(x))++‖h(x)‖
其中λ1(A)表示矩阵A的最大特征值, (α)+=max{0,α}, (λ1(G(x)))+简记为λ1(G(x))+. 显然, 若θ(x)=0, 则x为NLSDP(1) 的可行解.
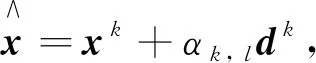
(3)
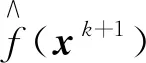
pred(xk)=-f(xk)Tdk
(4)
因此, 定义目标函数f(x)的非单调充分下降性条件:
nared(xk)≥ηαk,lpred(xk)
(5)
其中η∈(0, 1), 这不同于单调充分下降性条件:
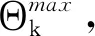
(6)
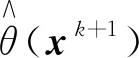
(7)
其中β∈(0, 1).
最后, 下面给出算法的接受准则. 如果约束违反度函数θ(x)满足非单调充分下降性条件, 即(7)式成立, 或目标函数f(x)具有适当的下降量且约束违反度函数值有个合理的上界, 即
(8)
成立, 其中γ∈(0, 1). 那么考虑以下两种情况.
1) 若
pred(xk)≤ξ(dk)TBkdk
(9)
且
(10)
2) 若
pred(xk)>ξ(dk)TBkdk
(11)
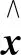
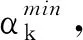
(12)
其中γα∈(0, 1),sθ≥1.
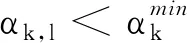
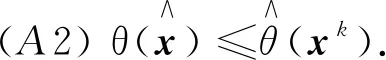
可行性恢复阶段的具体细节见文献[10].
基于以上讨论, 下面给出求解NLSDP(1)的算法描述:
算法1
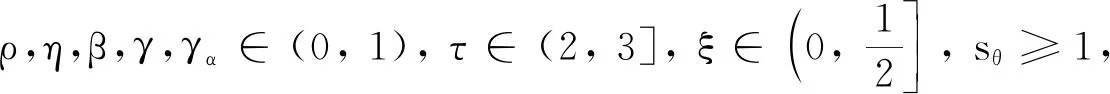
步骤1令flag=0, 求解子问题QSD(xk,Bk). 若QSD(xk,Bk)存在最优解, 则记为dk, 否则算法进入可行性恢复阶段, 转步骤7. 若dk=0, 则算法停止.
步骤3(回溯线搜索)
步骤3.1令l=0,αk,0=1.
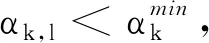
步骤3.3若(7)式和(8)式不成立, 则转步骤3.5.
步骤3.4若(9)式和(10)式成立, 则令flag=1, 转步骤4. 若(5)式和(11)式成立, 则转步骤4.
步骤3.5令αk, l+1=ραk, l,l=l+1, 转步骤3.2.
步骤4令αk=αk, l,xk+1=xk+αkdk.
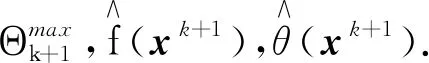
步骤6(更新步)利用某种方法, 更新Bk为对称正定矩阵Bk+1. 令k=k+1, 转步骤1.
2 全局收敛性
本节将分析算法1的全局收敛性, 为此, 需作如下合理假设:
(B1) 迭代点列{xk}和{xk+αk,ldk}在紧凸集χ中.
(B2)f(x),h(x),G(x)在紧凸集χ中二阶连续可微.
(B3) 矩阵Bk为对称正定矩阵, 且存在常数a,b>0, 对任意的d∈Rn有a‖d‖2≤dTBkd≤b‖d‖2.
注1不失一般性, 由假设B可知, 对于任意x∈χ, ‖2f(x)‖≤b, ‖D2h(x)‖≤b, ‖D2G(x)‖≤b.
引理1对于任意的k, 以下不等式成立:
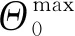
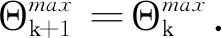
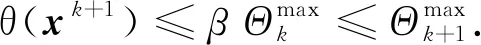
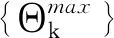
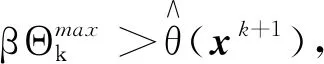
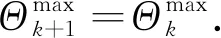
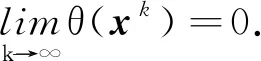


于是有
因此, 当k充分大时

2) 假定θ型迭代发生无限次, 那么存在指标k2, 使得当k>k2时,θ型迭代发生, 由(10)式和引理2, 可知结论成立.
引理4在假设B条件下, 子问题QSD(xk,Bk)的可行解d满足以下不等式:
(13)
(14)
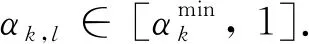
证由(3)式、 (4)式、 Taylor展开式和假设B可得
其中ξ1介于xk和xk+αk,ld之间. 类似地, 由Taylor展开式可推出
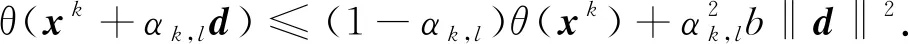
引理5在假设B成立下, NLSDP(1)的可行点x*满足MFCQ条件, 但不是KKT点. 那么存在x*的邻域N(x*)及正常数η1, 使得当xk∈N(x*)∩χ时, 子问题QSD(xk,Bk)的可行集非空, 且其最优解dk满足
(15)
证类似文献[14]的引理4.7可证结论成立.
引理6在假设B条件下,dk是子问题QSD(xk,Bk)的最优解, 那么若
(16)
且
(17)
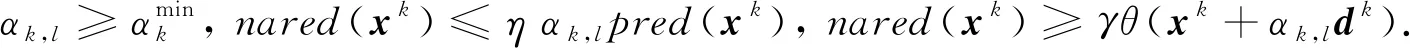
证若
则由引理4和引理5得
故nared(xk)≥ηαk,lpred(xk)成立. 结合引理4和引理5, 由(16)和(17)式有
故nared(xk)≥γθ(xk+αk,ldk)成立.
引理7在假设B条件下, 线搜索(步骤3)是有限步终止的.
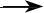
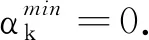
综上所述, 若
(18)
则xk+αk,ldk被算法所接受,f型迭代发生, 矛盾.

定理1若假设B成立, 则下面结论之一成立:
(C2) 算法有限步终止, 即存在某个迭代点xk为NLSDP(1)的KKT点.
(C3) 算法产生的迭代点列{xk}收敛于聚点x*且该聚点x*为NLSDP(1)的可行解, 那么x*或是NLSDP(1)的KKT点, 或是x*不满足MFCQ条件.
证不失一般性, 假设结论(C1)和(C2)都不成立, 下面讨论两种情况分别证明结论(C3)成立.
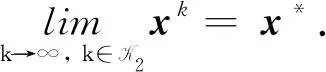
即x*是NLSDP(1)的可行点.
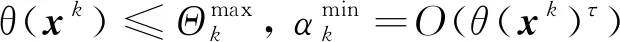
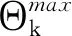
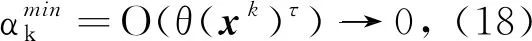
3 数值试验
为了验证算法1的可行性, 本节给出了算法的初步数值实验, 采用MATLAB(2014a)软件实现算法, 程序在配置Windows 10, 8G RAM, 3.60 GHz CPU的计算机上运行. 子问题QSD(xk,Bk)使用文献[15] SDPT3求解. 算法采用BFGS公式对Bk更新为Bk+1, 其更新公式见文献[16]. 下面给出算例问题如下:
1) Rosen-Suzuki问题: 测试算例来源于文献[17]:
其数值结果见表1.
2) SOFP问题. 测试算例来源于文献[18]:
其中:QF=CTFTFC+I;AF=A+BFC; 矩阵变量L为实对称的; 矩阵变量F不是方阵;A,B,C为常量矩阵. 该问题的数值结果见表2.

表2 SOFP问题数值结果
3) NCMP问题. 测试算例来自于文献[9]:
其中:A=(aij)(∈Sm)是给定的, 且其对角线元素aii=1(i=1,2,…,m), 其余元素随机取自[-1, 1]; 选取ε=10-3. 数值结果见表3.
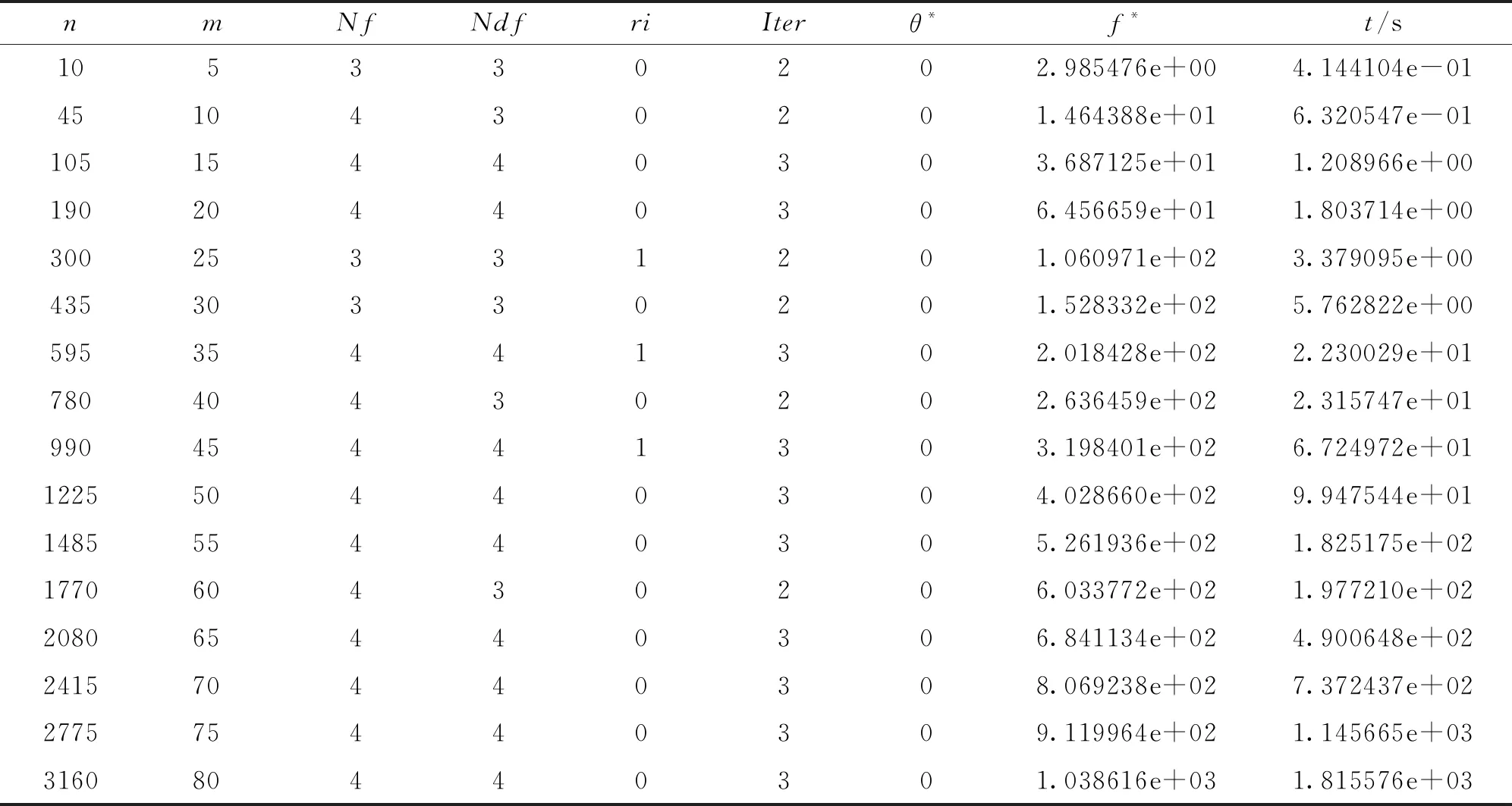
表3 NCMP问题数值结果
在数值试验中, 选取的参数如下:
η=0.001,τ=0.01,ξ=0.01,γ=0.001,γα=0.99,sθ=2,β=0.999,ρ=0.5
终止准则为‖dk‖≤10-4, 设置算法1的迭代次数上限为200. 下面给出表1-3中的符号含义如下:x0为初始点;Ndf为目标函数梯度计算次数; problem为COMPleib算例库算例名称;Iter为算法迭代次数;n为自变量维数;ri为可行性恢复阶段使用次数;p为等式约束的维数;θ*为最优点约束违反度函数值;m为半定约束矩阵维数;f*为最优目标函数值;Nf为目标函数计算次数;t为计算机运行时间(含可行性恢复阶段用时).
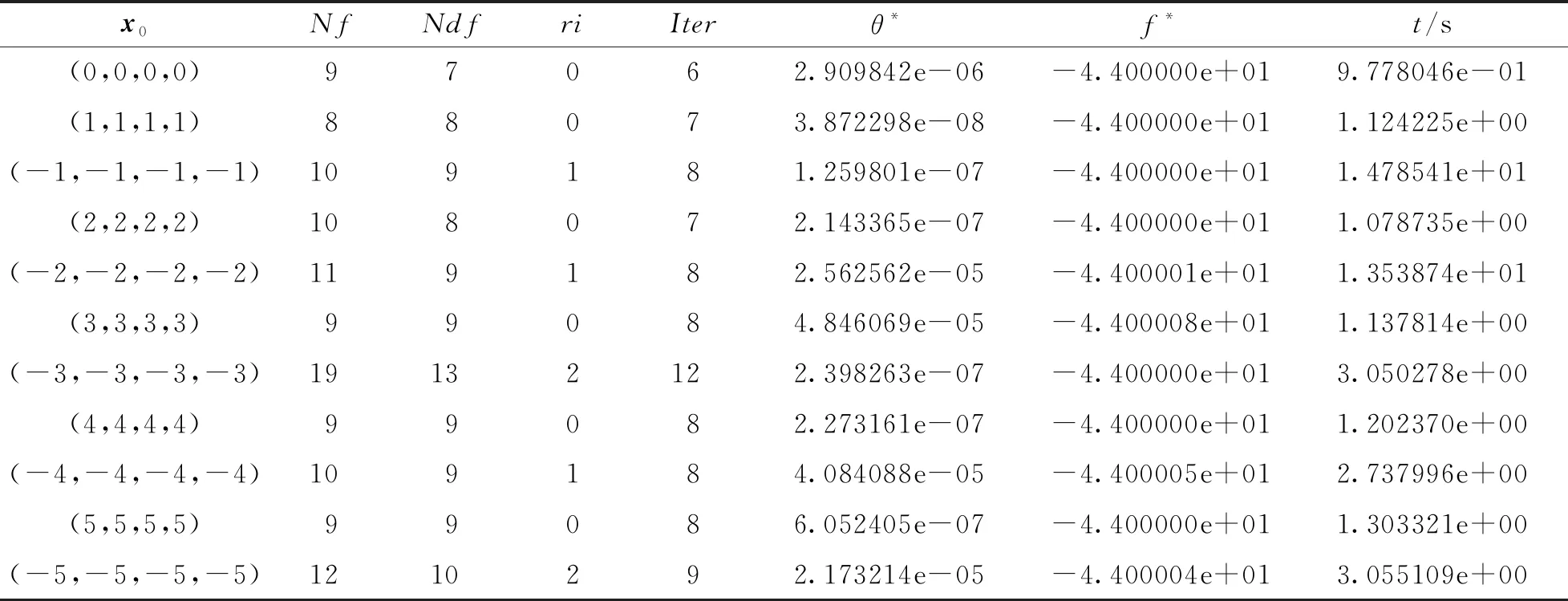
表1 Rosen-Suzuki问题数值结果
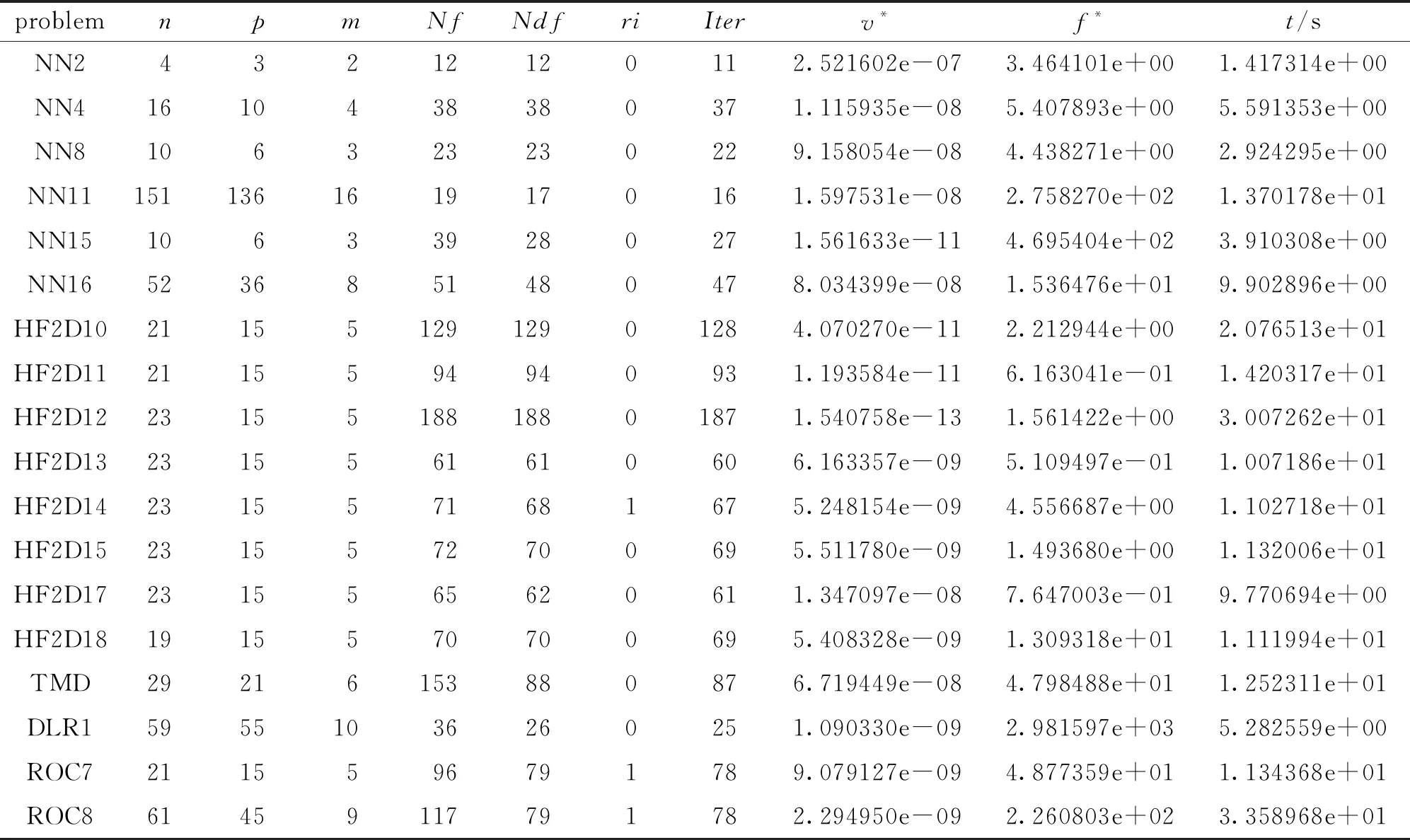
续表2
4 小结
本文提出一种新的求解非线性半定规划的无罚无滤回溯线搜索型序列半定规划算法, 新方法基于传统的二次规划子问题构建二次半定子问题, 通过求解该子问题产生搜索方向, 为了避免使用罚函数和滤子, 采用回溯线搜索技术来保证目标函数值或约束违反度函数值充分下降. 而非单调的充分性下降条件使得试探点更加容易被算法接受. 同时在合理的假设条件下, 证明了该算法的适定性以及全局收敛性, 最后初步的数值试验结果表明了该算法的有效性.

